利用几何知识求解函数的最值

吴丽丽

(福建省漳州市第三中学 363000)

在当前利用几何知识求解函数最值中，主要包括了向量法、数形结合法等.数形结合法包括了把最值转化为函数图象的截距，把最值转化为两个函数图象上点的距离、 或两点连线的斜率等.

一、运用向量法求解函数最值

在高考中，向量是一个较为重要的部分，利用直观的图形，对很多代数式进行转化，从而便于理解.利用向量求解函数最值，需要掌握向量的特点，分别是向量三角不等式：|a|+|b|≥|a+b| ；向量数量积性质：a·b≤|a||b|.在应用向量法的过程中，要确保合理恰当地构造向量，根据函数形式选择最合适的向量，以保证能够在有限的时间内快速求解函数最值.而且，向量法中会涉及到很多不等式，因此在实际解题过程中，需要对不等式的等号成立条件加以注意.

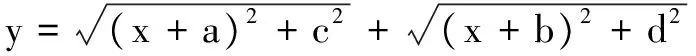
二、运用构造法求解函数最值

在函数问题中，构造法是一种常用的解题方法，在利用几何知识求解函数最值的过程中，也会对构造法加以应用.

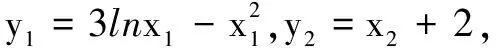
解根据题目构造两个函数f(x)=3lnx-x2,g(x)=x+2，设A(x1,y1),B(x2,y2),点A、B分别为函数f(x)=3lnx-x2、g(x)=x+2图象上的两个动点, 则|AB|2=(x1-x2)2+(y1-y2)2.

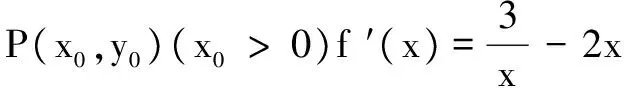
分析对题中给出的信息加以分析，对满足题目要求，同时方便求解的图形进行构造，为函数最值求解提供帮助.在平常的学习中应当注意对图形的观察，从而能够在解决实际问题时更加得心应手.

三、转化为截距求解函数最值

高考当中会有一些数学问题，并没有直接给出函数求解，而是需要构造一个函数，然后转化成数形结合方法，对函数最值进行求解.最为常见的是一次函数y=kx+b的截距，此类一次函数的构造相对简单而且计算方便，使x=0或y=0即可求解最值.

例3 (2017年南宁模拟)已知M(m,n)为圆C:x2+y2-4x+14y+45=0上任意一点，求m+2n的最大值.

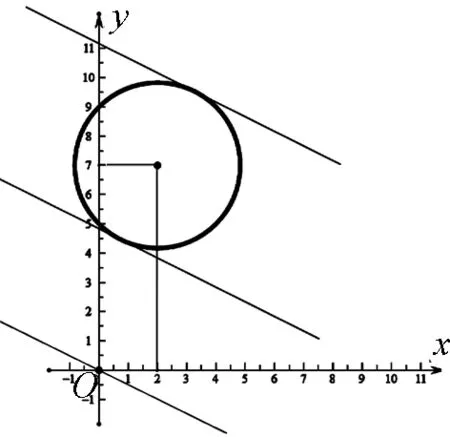
分析此类题目相对较为简单，没有设置过多的陷阱，求解的是二元一次多项式，但并不是本文提到的函数.对此，首先构造熟悉的函数，将问题转化为求解函数在y轴上的截距问题，同时可画图辅助分析，得到更为清晰的解题思路.

总之， 高考对于数形结合思想方法的考查， 就是一大要点.我们要有意识地引导学生运用几何方法去分析问题，让他们在面对高考中的特殊函数最值问题时，能从容应对.

参考文献：

[1]刘海洋. 立体几何最值问题的求解策略[J].中学生数理化:高二高三版, 2015(12):6-8.

[2]张礼恩.函数最值求解常用“十策”[J].数学之友, 2012(4):54-55.

[3]杨柳. 浅谈如何求解分式三角函数最值[J].中学课程辅导:教师教育, 2013(22):91-91.