基于Halcon的弹芯尺寸精密检测算法研究*

陈茜茜， 王晓凯， 赵晓宏

(1. 山西大学 物理电子工程学院， 山西 太原 030006； 2. 山西迪迈沃科光电工业有限公司， 山西 太原 030006)

0　引　言

随着国防工业的快速发展及武器性能的提高， 对批量生产的炮弹等武器的零件参数要求越来越高[1]， 且弹芯零件的生产是流水线式、 产量高、 速度快. 而我国目前对弹芯零件采取的仍是接触式的传统检测方法， 这种方法检测效率低、 可靠性差， 使得结果的准确性不能保证. 随着近年来机器视觉的快速发展， 将视觉检测技术引入工业实际生产检测中， 可以实现对零件尺寸的高精度、 非接触及实时在线的检测[2,3]. 因此这种非接触式测量法满足了弹芯生产过程中的检测节拍高速化、 数据采集实时化、 生产过程智能化[4]的要求， 从而保证了弹芯生产的质量和数量.

本文以Halcon软件为开发平台， 通过亚像素级阈值分割提取出轮廓并进行边缘拟合， 最终实现对弹芯的高精度尺寸检测. 通过多次实验， 本文算法在某公司的弹芯尺寸检测项目上得到了较好的应用.

1　弹芯尺寸视觉检测系统

视觉检测系统包括图像采集[5]、 图像处理、 结果输出与执行3部分[6]. 图像采集系统由一个工业面阵相机、 一个远心镜头及一个远心平行光源组成， 且视觉检测系统的中心安装有摆放平台， 采用背光照明的打光方式并通过工业相机拍照来抓取弹芯上端部分的外形轮廓图片， 由于弹芯尺寸较小且检测精度为小于0.01 mm， 因此需选用高分辨率的相机才能对其进行识别检测， 该系统中相机选用的是1 000万像素分辨率的Basler面阵相机， 其型号为acA3800-10gm， 视觉检测示意图如图 1 所示.

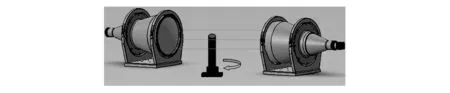
图 1　弹芯上端部分视觉检测示意图Fig.1　Schematic diagram of vision inspection of bullet upper part

该系统的总体工作流程如图 2 所示.

图 2　系统总体工作流程图Fig.2　The workflow diagram of the system

系统上电后， 系统的各模块部分进行初始化， 机械臂抓取工件放到摆放平台上， 然后机械臂抬升到一定高度后， 会向PLC发送信号， PLC被触发并控制相机采集弹芯零件图像， 并送到图像队列中. 图像处理软件读取图像， 并对各指标进行检测， 判断其是否在精度要求范围内， 进而判断零件是OK产品还是NG产品. 最后， 将该检测信号反馈给机械臂， 机械臂依据分拣信号将工件有序放在合格品、 残次品分拣口处.

2　基于Halcon的亚像素级检测算法

本文中弹芯的主要检测参数包括： 弹芯球头半径、 球头高度、 弹芯直径， 这3个参数的标准值分别为4 mm， 5 mm， 15 mm. 其涉及的算法有： 亚像素精度阈值分割、 特征提取[7]、 边缘分割、 亚像素边缘拟合等， 算法的具体流程如图 3 所示. 视觉检测系统对弹芯上端部分进行采图， 获得的图像如图 4 所示. 采集到的图像为灰度图像， 大小为3 840*2 748像素.

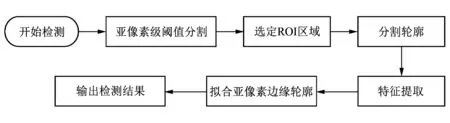
图 3　弹芯尺寸检测算法流程 Fig.3　Flow chart of bullet core size detection algorithm

图 4　弹芯上端部分图像 Fig.4　Diagram of bullet upper part

2.1　亚像素级阈值分割

工业面阵相机CCD， CMOS芯片的成像面以像素为最小单位， 相机拍摄时， 将物理世界的连续图像进行了离散化处理[8]， 因此这些像素所反映的只是图像中特定邻域内的亮度信息， 其相邻像素间仍存在着微米级的距离， 为了更精确地提取出图像的有效信息并提高其分辨率， 可以将像素距离进行区域细分， 即采用亚像素的方法来提高分辨率. 由于在实际工业检测中， 提高硬件系统分辨率的成本代价很高， 因此通过软件算法来提高图像处理中高精度定位问题具有非常重要的意义.

图 5　双线性插值法原理图Fig.5　Schematic diagram of bilinear interpolation method

经典的阈值分割算法[9]获得的边缘轮廓属于像素级， 其提取出的边缘呈锯齿状， 会对定位精度产生很大影响. 而亚像素级阈值分割则是通过使用双线性插值法， 得到一系列相邻的、 连续的采样点集合， 从而实现了像素的细化， 这些采样点的灰度值为gsub， 所以最终的边缘轮廓就可看作用连续的边缘函数f(r,c)与常量函数g(r,c)=gsub相交得到.

双线性插值法的本质即为分别对x,y方向进行插值运算， 如图 5 所示， 选取插值点P(x,y)的4个相邻像素点P11(x1,y1),P12(x1,y2),P21(x2,y1),P22(x2,y2)， 假设亮度函数在这个邻域内是线性的， 分别计算P(x,y)到这4个相邻点的水平距离和垂直距离， 并求出不同灰度级所占的权重大小， 即可获得插值点P(x,y)的灰度值， 通常距离值与权重值成反比.

函数g表示像素点的灰度值， 首先对x方向进行线性插值， 可得

(1)

(2)

然后在y方向进行线性插值， 则P(x,y)像素点的灰度值

(3)

将式(3)化简后可推算出

(4)

通过上述计算得到的插值点P(x,y)的灰度值通常为浮点数， 对其进行四舍五入， 并将所有的插值点进行连接， 即可得到亚像素阈值分割后的边缘轮廓.

图 6　亚像素级阈值分割的轮廓 Fig.6　Sub-pixel threshold segmentation contour

图 7　亚像素边缘局部放大图Fig.7　Partial enlargement diagram of sub-pixel edge

根据弹芯零件的灰度值分布， 选取阈值gsub=80， 并使用双线性插值提取亚像素边缘， 可得到如图 6 所示的效果图， 其局部放大图如图 7 所示， 亚像素阈值分割后提取出了弹芯轮廓. 从图 7 中可以看出， 插值后的亚像素边缘比较平滑、 未产生锯齿， 效果较为理想.

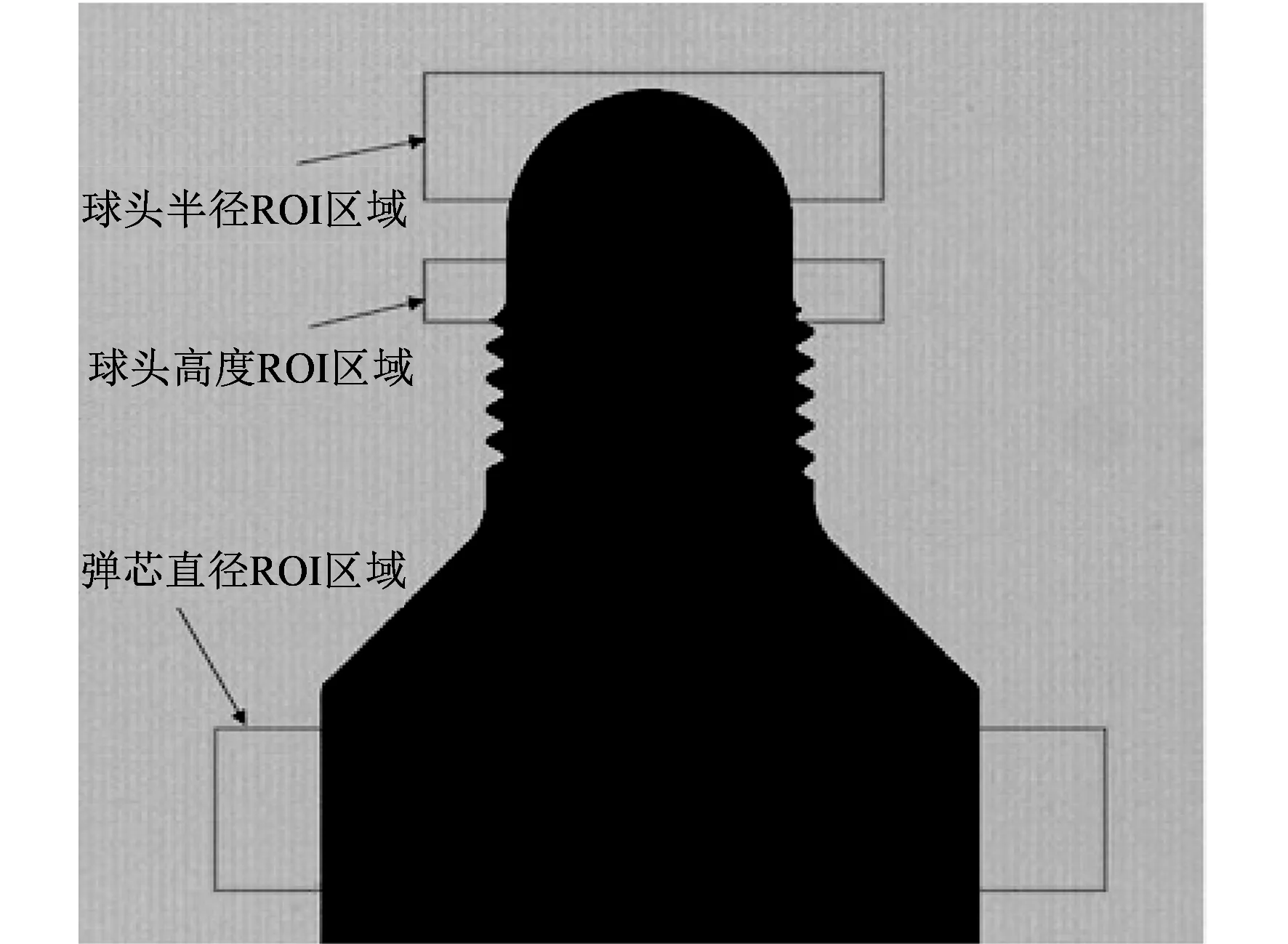
图 8　3个检测参数的ROI区域Fig.8　The ROI area of three test parameters

2.2　选定ROI区域

该系统中机械臂的选型为SCARA 4轴机械臂， 其重复运动精度为0.1 mm. 由于相机的安装高度、 位置等固定不变， 因此机械臂在多次抓取零件放至摆放平台上并进行采图的过程中， 零件在图像中仅存在水平方向较小的位置偏差， 并不影响对图像的处理， 所以可人工选定相应的ROI区域.

Halcon中可通过算子gen_rectangle1 (ROI,Row1,Column1,Row2,Column2)来设置弹芯各检测参数的感兴趣区域(ROI区域)， 从而减少了后续处理的数据量， 并提高了图像处理的速度. 本文3个检测参数的ROI区域如图 8 所示.

2.3　轮廓分割及特征提取

由图 6 可知， 提取出的亚像素轮廓虽然是连续的， 但并非严格的标准圆弧或线段. 以球头半径参数为例， 为了更精确地拟合出ROI区域中弹芯球头所在的标准圆， 进而求出球头半径， 需要对轮廓进行分割， 并进行若干次特征提取， 以把非弹芯的干扰轮廓去除掉. 本文采用Ramer逼近算法来分割轮廓， 假设边缘轮廓点集为pi(r,c),i=1,…,n， 通过使用多边形近似来找到轮廓点的一个子集pij,j=1,…,m,m≤n， 其中该多边形的每条线段(pij,pij+1)就近似表示轮廓.

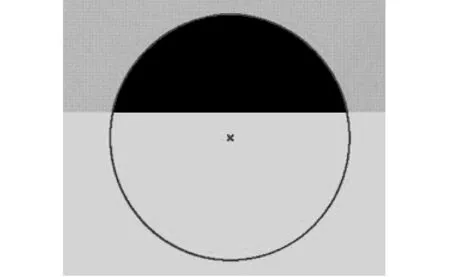
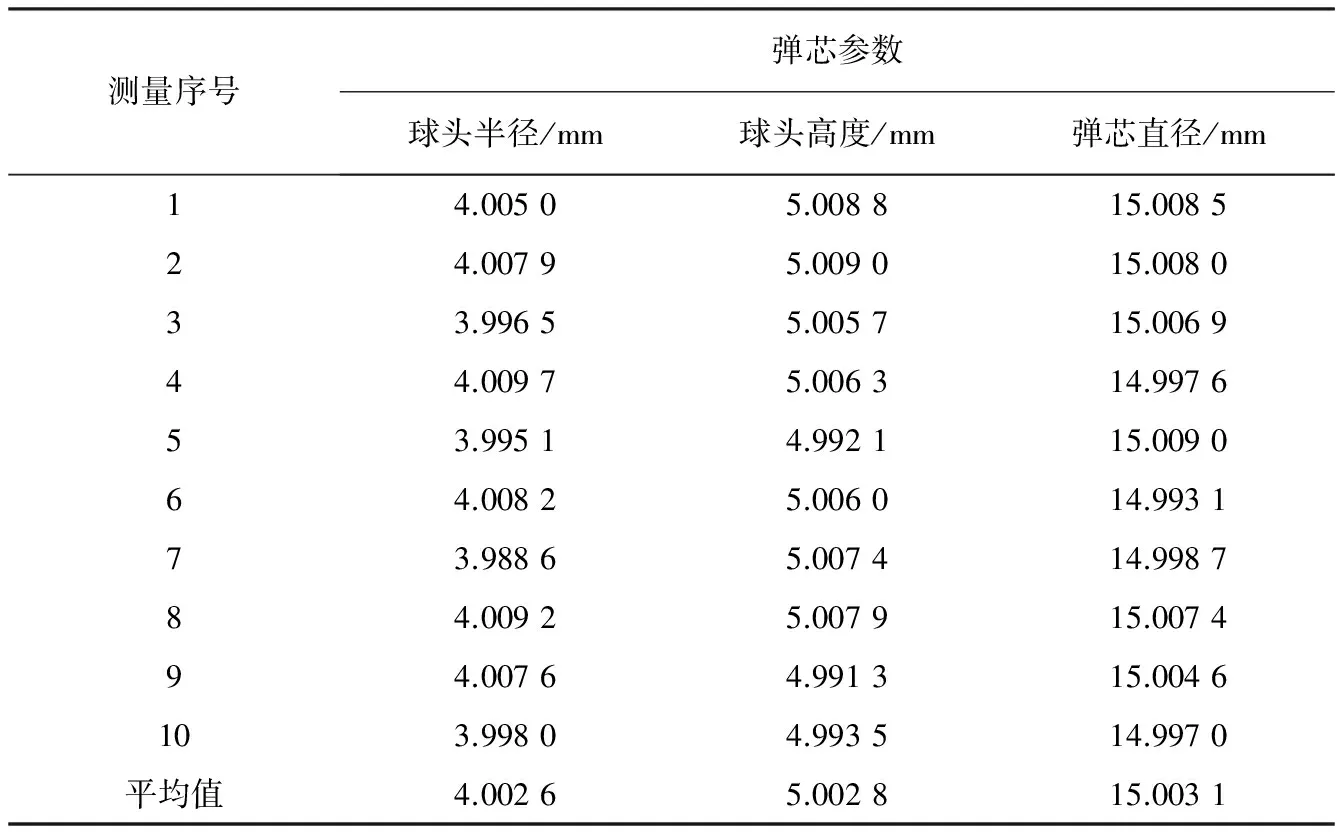
Ramer算法采用了区域分裂、 合并来实现递归逼近， 首先通过分裂操作将曲线轮廓分割成若干条线段， 即确定轮廓的起始点和终止点， 并进行线段连接， 然后计算轮廓上所有点到这条线段的距离， 并求取出其距离最大值dmax， 假设所设定的距离阈值为dset， 若dmax>dset， 则在dmax所对应轮廓点处， 将当前线段分割成两条新的线段， 以此递归重复， 然后采用合并操作将相邻的两条线段进行合并， 直到曲线轮廓与所有逼近线段之间均满足dmax

可使用segment_contours_xld(Border,ContoursSplit,‘lines’,5,4,2)将轮廓进行分割， 为了从分割结果中剔除干扰边缘， 根据检测对象的长度、 圆度等特征进行特征提取， 使用算子select_shape_xld(ContoursSplit,SelectedContours,‘contlength’,‘and’,85,105)来获取理想的边缘.

2.4　拟合亚像素边缘轮廓

使用Ramer算法将轮廓分割后， 有时会存在个别轮廓点稍微偏离真实位置的情况， 为了更精确地获取到待检参数值， 需要对轮廓进行拟合实现. 本文以拟合弹芯球头的标准圆为例重点阐述， 拟合直线算法类似. 先用传统的最小二乘法[10,11]拟合得到一个圆， 然后计算轮廓中所有点到该拟合圆的距离， 并根据权重函数w(δ)来确定轮廓点所具有的权重值， 通常距离值越小， 所具有的权重就越大.

边缘轮廓点为pi(ri,ci)， 设拟合圆的半径为ρ， 圆心坐标为(a,b)， 则拟合圆的方程为

(ri-a)2+(ci-b)2=ρ2.

(5)

假定没有落在拟合圆上的轮廓点的误差为ε， 为了使误差值始终为正， 使用误差平方和来表示

(6)

根据最小二乘法原理， 求取误差平方和最小时的各参数值， 其中Ω表示边缘轮廓的像素点集， 即

(7)

但是由于采用平方距离， 最小二乘拟合算法对于大的离群点鲁棒性差， 且这些离群点的权重ω(δ)很大[12]. 因此， 为了减少这些离群点的影响， 使拟合的效果达到最好， 合理定义权重ω(δ)就非常重要， 本文采用Tukey权重函数， 其定义为

(8)

图 9　球头半径ROI区域的拟合圆Fig.9　Fitting circle of the ROI area of the ball head radius

式中：δ是各轮廓点到拟合圆的距离;τ是削波因数， 此权重函数将距离δ>τ的点视为离群点并完全忽略， 而对于距离δ≤τ的点， 其权重值在0～1之间变化.

Halcon中算子fit_circle_contour_xld(Border,‘atukey’, -1, 0, 0, 3, 2, Row, Column, Radius, StartPhi, EndPhi, PointOrder)将部分圆弧线段拟合成圆， 其中第7个参数ClippingFactor=2， 该参数即为削波因数， 其值越小， 检测到的离群点则越多， 该算子返回拟合圆的相关参数， 其中半径Radius即为弹芯球头半径. 球头高度及弹芯直径的检测与球头半径的检测原理类似， 这里不再赘述. 对这3个参数ROI区域的轮廓进行拟合， 其拟合结果如图 9～图 11 所示. 可见拟合后的亚像素边缘轮廓.

图 10　球头高度ROI区域的拟合直线 Fig.10　Fitting line of the ROI area of the ball height

图 11　弹芯直径ROI区域的拟合直线Fig.11　Fitting line of the ROI area of the bullet diameter

3　实验结果与分析

经过图像处理后的弹芯尺寸是以像素为单位的， 其像素尺寸测量结果如表 1 所示.

表 1　弹芯各参数测量结果

由于远心镜头具有极佳远心度、 超低畸变等特点， 使得物体成像比工业普通相机更加准确， 其畸变一般都小于0.1%， 因此可忽略畸变系数的影响. 为了获得实际物理尺寸和像素值之间的转换关系[13,14]， 即标定系数K， 选取标准弹芯来对系统进行标定， 其计算步骤如下：

1) 已知标准弹芯的弹芯直径为

dmm=15.0 mm.

(9)

2) 保证光源、 相机等硬件系统环境始终不变， 利用本文算法得到该标准弹芯的弹芯直径像素尺寸

dpixel=1 594.049.

(10)

3) 计算标定系数

(11)

确定K值后， 即可得到弹芯各参数实际物理尺寸值， 随机选取多个弹芯零件利用本文算法进行测量， 以10组检测结果为例， 其测量结果如表 2 所示.

表 2　弹芯各参数物理尺寸测量结果

由表 2 中的数据可知： 测量结果的平均值很接近其标准值， 且其值与标准值的偏差均小于0.01 mm， 达到了检测精度要求. 从上述的实验分析， 可以得出本文算法能够满足弹芯尺寸的在线检测， 该方法检测精度高、 效率快.

4　结束语

本文以Halcon软件为平台， 设计了一种准确、 高效计算弹芯亚像素级尺寸的算法， 该算法通过软件实现了弹芯亚像素级轮廓的确定， 通过实验数据可以发现， 其检测结果值与标准值的偏差小于0.01mm， 达到了检测精度要求， 实验结果表明可以满足检测过程对稳定性、 准确性的要求. 而弹芯零件的其他检测参数如体积、 缺陷等对其批量生产也产生很大的影响， 这将是笔者对弹芯零件检测的下一步研究方向.

参考文献：

[1]李红钢. 基于机器视觉的某型药筒零件难测量尺寸测量系统研究[D]. 太原： 中北大学, 2014.

[2]陈艺峰. Halcon在工件二维尺寸检测上的应用[J]. 机电技术, 2011, 34(4)： 12-13.

Chen Yifeng. The application of Halcon in the dime-nsion detection of workpiece[J]. Mechanical & Electrical Technology, 2011, 34(4)： 12-13. (in Chinese)

[3]师雪超, 孙振忠, 卢盛林, 等. 基于机器视觉的弧形件检测算法[J]. 计算机应用, 2010, 30(7)： 1841-1843.

Shi Xuechao, Sun Zhenzhong, Lu Shenglin, et al. Inspection algorithm of arc-parts based on machine vision[J]. Journal of Computer Applications, 2010, 30(7)： 1841-1843. (in Chinese)

[4]陈云. 基于机器视觉的SMD管脚尺寸检测[D]. 上海： 上海交通大学, 2011.

[5]Rafael C G, Richard E W. 数字图像处理[M]. 阮秋琦, 阮宇智, 译. 第3版. 北京： 电子工业出版社, 2007.

[6]唐松, 杨其华, 刘刚海. 基于Halcon的阀芯尺寸亚像素级测量[J]. 计算机工程与应用, 2017, 53(3)： 237-241.

Tang Song, Yang Qihua, LIU Ganghai. Valve core size sub-pixel measurement based on Halcon[J]. Computer Engineering and Applications, 2017, 53(3)： 237-241. (in Chinese)

[7]关波, 王俊元, 杜文华, 等. 刀具轮廓亚像素精度阈值分割算法研究[J]. 图学学报, 2014, 35(6)： 950-953.

Guan Bo, Wang Junyuan, Du Wenhua, et al. Research on sub-pixel precise thresholding for tool contour extraction[J]. Journal of Graphics, 2014, 35(6)： 950-953. (in Chinese)

[8]Milan S, Vaclav H, Roger B. 图像处理、 分析与机器视觉[M]. 艾海舟, 苏延超, 译. 第3版. 北京： 清华大学出版社, 2011.

[9]Carsten S, Markus U, Christian W. 机器视觉算法与应用[M]. 杨少荣, 吴迪靖, 段德山, 译. 北京： 清华大学出版社, 2008.

[10]张艳莉. 基于最小二乘法拟合直线的研究[J]. 信息通信, 2014(11)： 44-45.

Zhang Yanli. Study on curve fitting based on least square method[J]. Information & Communications, 2014(11)： 44-45. (in Chinese)

[11]Lopez-Molina C, Baets B D, Bustince H, et al. Multiscale edge detection based on Gaussian smoothing and edge tracking[J]. Knowledge-Based Systems, 2013, 44(1)： 101-111.

[12]张宝峰, 王明跃, 朱均超. 一种零件图像亚像素边缘检测算法[J]. 计算机仿真, 2014, 31(2)： 288-292.

Zhang Baofeng, Wang Mingyue, Zhu Junchao. Edge detection algorithm of parts image sub-pixel[J]. Computer Simulation, 2014, 31(2)： 288-292. (in Chinese)

[13]王健, 曾光宇. 基于单幅图像的摄像机标定[J]. 微计算机信息, 2010, 26(19)： 215-216.

Wang Jian, Zeng Guangyu. Camera calibration based on single image[J]. Microcomputer Information, 2010, 26(19)： 215-216. (in Chinese)

[14]Heikkila T, Sallinen M, Matsushita T, et al. Flexible hand-eye calibration for multi-camera systems [C]. Proceeding of 2000 IEEE/RSJ International Conference on Intelligent Robots and Systems. Takamatsu： IEEE, 2000： 2292-2297.