基于自适应卡尔曼滤波的超宽带室内定位系统*

童基均， 金利剑， 赵英杰， 高法钦， 柏雁捷

(浙江理工大学 信息学院， 浙江 杭州 310018)

0　引　言

随着物联网技术的发展以及室内导航应用的需求日益提高， 精确的室内定位技术成为了各大研究机构以及企业的研究热点. 但由于室内无线环境复杂， 无线信道混乱， 原有的室内定位方案无法满足精度要求[1]， 而基于超宽带(Ultra Wideband， UWB)的室内定位方案以其抗干扰、 抗多径传播能力强以及低功耗， 低成本， 高精度等特点， 得到了越来越多人的关注[2]. 比如微软室内定位大赛是国际盛名的室内定位大赛(MS Indoor LOC Competition)， 从2014年开始举办， 每年都能吸引大量的公司和高校团队参加， 其中基于UWB的室内定位技术占据了半壁江山.

基于UWB室内定位技术常用的方法有信号到达角度AOA， 信号到达时刻TOA， 信号到达时差TDOA和信号强度RSSI[3]. 其中AOA和RSSI方法单独使用时在复杂的室内环境下无法有效的保证定位精度， 一般作为TOA与TDOA的辅助方法使用[4-6]. 而TDOA是在TOA基础上进行改进的方法， 具有定位精度高、 抗多径能力强等特点， 无需基站和移动目标时间上的严格同步， 实际应用中更易实现[7]. 目前大部分基于UWB的室内定位系统都是采用TDOA方法定位的.

目前， TDOA最常用的算法是Chan算法[8]. Chan使用了两次最小二乘计算， 在定位基站个数大于4个， 且在LOS环境下定位时， 可以达到克拉美罗下限[9]. 但是， Chan算法对环境的依赖较高， 在定位范围内出现物体遮挡， 或在NLOS环境下时， 定位误差较大. 因此， 论文[10]提出了Chan算法与Taylor展开法相结合的定位方法[10]， 保证了Taylor算法的快速收敛. 此外， 论文[11]提出了利用卡尔曼滤波与Chan算法相结合的方法[11]. 文中比对了各种卡尔曼滤波算法与Chan算法结合运算后的定位结果， 发现结合了卡尔曼滤波的定位算法精度更高， 可靠性更强. 对于卡尔曼滤波的应用， 论文[12]和[13]发现将时延信息通过卡尔曼滤波处理后再进行定位， 可以获得更高精度的定位结果[12,13].

当传统的卡尔曼滤波用于定位时， 对于滤波所需要的协方差系数等先验知识难以准确取得， 且在系统运行过程中， 由于环境因数的改变或是基站长时间运行导致的测量结果发生温漂等现象时， 传统的卡尔曼滤波无法有效应对环境产生的干扰和测量值的变化. 因此本文提出了一种自适应卡尔曼滤波算法， 可以根据历史值估算测量误差Rk和过程误差Qk并自动更新， 有效地减少了TDOA值误差， 提高了定位精度.

1　自适应卡尔曼滤波

传统的卡尔曼滤波方法分为预测和更新两步[14,15]， 其中预测阶段的步骤为

(1)

式中：xk为预测值；xk-1为上一时刻的值；Pk为误差协方差矩阵；Fx为状态变换矩阵；bk为控制输入；uk为控制矩阵.

更新阶段的步骤为

(2)

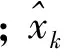
在卡尔曼滤波中，Qk和Rk分别为过程误差和测量误差的协方差矩阵， 但他们在现实中很难精确求得， 且在系统运行过程中也常常会发生变化， 从而影响定位精度. 对此我们使用了可以动态调整Qk和Rk值的自适应卡尔曼滤波算法. 通过极大似然准则，Rk由式(3)计算得到

(3)

另有

(4)

式中：N表示了所需要考虑的历史值的个数. 因此测量误差协方差矩阵Rk可以由式(5)计算得到

(5)

根据式(3)的方程组， 即可得出过程误差协方差矩阵

(6)

为了方便计算， 将式(6)变形为

(7)

由式(2)可知

(8)

并且

(9)

由于误差协方差矩阵Pk为对称矩阵， 因此过程误差协方差矩阵Qk的计算过程可以表示为

(10)

2　UWB系统实现

2.1　UWB系统架构

本文设计的定位系统如图 1 所示， 整个系统由时间同步基站， 定位基站， 移动标签以及定位服务器组成. 同步基站负责基站之间的时间同步， 定位基站收到定位标签信息后， 通过以太网将各个标签的时间戳信息传给定位服务器. 定位服务器根据各种定位算法计算出标签位置信息.

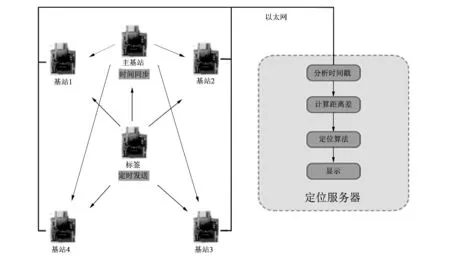
图 1　基于TDOA的UWB定位系统架构图Fig.1　The schematic of UWB position system based on TDOA

图 2　标签与基站实物图Fig.2　The pictures of tags and base station

2.2　标签与基站的硬件实现

采用DecaWave公司生产的DW1000芯片， 通过STM32单片机， 实现了移动芯片和基站的设计. 移动标签使用了方便携带的陶瓷芯片， 如图 2(a) 所示， 定位基站设计中增加了全向天线和增益电路， 如图 2(b) 所示. 标签与基站都使用W5500以太网网络模块通过千兆交换机与定位服务器相连.

2.3　时间同步方法

基站之间的时间同步方法有多种， 常用的有TWR测距方法、 SDS-TWR测距方法[16]和基于时差提取等方法[17]. 其中TWR测距方法与SDS-TWR测距方法需要计算出每个基站距离标签的距离后再计算距离差， 基站与标签之间的通信时间长且容易造成碰撞， 本文中采用了基于时差提取的方法， 这种时钟同步方案采用标签和基站之间的双向握手通信， 因此基站之间不需要严格的参考时钟， 并且增加定位基站数量并不会增加系统的同步时间以及复杂度. 其原理如图 3 所示.

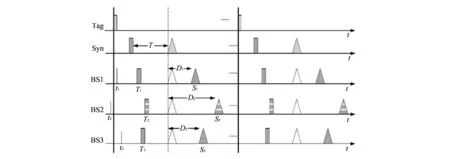
图 3　时钟同步时序图Fig.3　Timing diagram of clock synchronization

图 3 中， 标签Tag等间隔地发送定位信号，T1,T2,T3分别为各基站接收到来自标签的定位信号到达时刻. 同步基站(Syn)接收到标签信号后延迟T秒发送信号， 假定间隔T足够大， 可以保证所有基站能够接收完同步基站(Syn)发出的基准信号.T为设定的固定值.t1,t2,t3分别是BS1, BS2及BS3的开始工作时间(未知量)；S1,S2,S3是分别是BS1, BS2, BS3收到的来自同步基站(Syn)的基准信号到达时刻；D1,D2,D3是同步基站(Syn)与定位基站BSi(i=1, 2, 3)之间的传输时延(同步基站(Syn)与定位基站位置固定， 该时延可计算得到)； 则TDOA的值可由式(11)得到， 其中Tij表示信号从标签到定位基站BSi与定位基站BSj(i≠j)之间的TDOA值(时间差).

(11)

2.4　定位算法

目前国内定位算法大多数采用的是Taylor级数展开法和Chan算法[18]， 在其它方面如解混叠解交织等细节方面目前相关的跟踪研究都很少见到. 该算法采用二次估计方法实现对MS位置的估计， 计算简单、 定位精度高具有很大的实用价值[19]. 在二维定位中， 若要利用Chan算法进行定位， 则基站数目必须大于等于4个， 也即列出的方程粗个数必须大于未知数个数. 如此才能充分利用Chan算法的定位优势[20]. 但Chan算法在非视距传输及信道性能较差的情况下, 定位精度会下降[21]， 因此传统的定位方法会在Chan算法之后使用Taylor级数展开法[22]进行一次次递归来逐步比较真实值.

在本文系统中， 将时延信息经自适应卡尔曼滤波处理后， 使用Chan算法进行定位， 并将其与传统的定位方法进行对比.

2.5　定位服务器

定位服务器使用了4核8线程的英特尔i7-4790K处理器， 16 GB内存. 所使用的定位程序在Visual Studio2015的平台上开发， 使用了windows窗体控件及C#语言编写， 运行界面如图 4 所示. 定位开始前系统需要先输入基站坐标， 其中左下方显示标签坐标信息， 右下方可以显示运动轨迹， 可以直观地展示标签的位置信息.

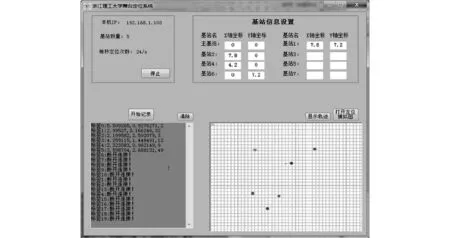
图 4　上位机界面Fig.4　The GUI of application system

3　系统测试与分析

3.1　实验设计

本实验在8 m×7 m大小的空旷室内场地中进行， 使用了4个定位基站， 放置在4个角落. 实验中将采用自适应卡尔曼滤波的改进定位方法与使用了Chan算法配合Taylor级数展开法的传统定位方法相比较， 分别测试了标签在固定位置时和在运动状态下不同定位方法的定位精度. 在自适应卡尔曼滤波算法的初始值设置中， 为了测试参数的校准能力， 将过程误差矩阵Qk、 测量误差矩阵Rk和误差协方差矩阵Pk的矩阵系数都设置为10. 状态变换矩阵Fx为[1,1;0,1]， 状态转移矩阵Hk为[1,0;0,0].

3.2　测试结果

3.2.1固定标签定位

实验测定了定位标签在场地中4个位置的定位信息， 定位结果为： 其中的平均位置偏差为测出的目标节点的位置与其实际位置的欧氏距离偏差, 每个位置分别测量了15次. 在标签静止时， 使用自适应卡尔曼滤波后的定位结果与传统定位方法的定位结果相比， 定位精度无太大变化， 但均方根误差有了很大的提高. 说明与传统定位方法相比， 使用自适应卡尔曼滤波算法优化后， 定位结果更为稳定.

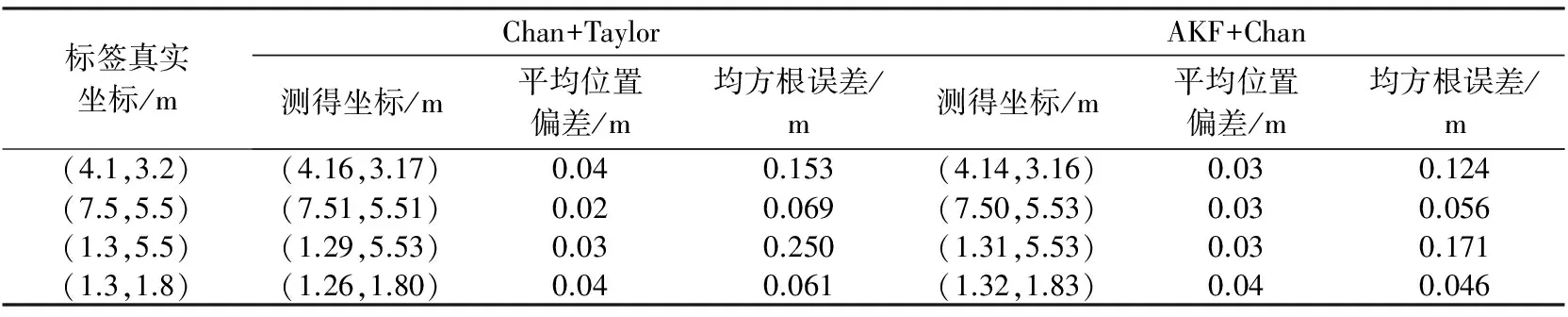
表 1　两种定位算法下的固定标签定位精度比较

3.2.2移动标签定位

本文同时测试了标签在移动状态下的定位结果. 其结果如图 5 所示， 其中粗线代表真实路径， 细线为传统的Chan算法与Taylor算法结合后测出的目标节点的位置后形成的路径， 点划线表示定位基站测得的TDOA值经自适应卡尔曼滤波处理后再由Chan算法测出的目标节点的位置后形成的路径.

图 5　定位系统轨迹图(m)Fig.5　The track of positioning system(m)

将采样点坐标与行走轨迹曲线之间的距离定义为测量偏差， 对比分析每一条行走路径的定位偏差， 结果如表 2 所示. 其中的平均位置偏差为测出的目标节点的位置与其实际位置的欧氏距离偏差.

表 2　两种定位算法下的移动标签定位精度比较

由此可以看出， 标签运动时使用了自适应卡尔曼滤波后的定位结果比传统的定位方法精度更高， 且提高了定位的稳定性.

4　结　论

本文采用了自适应卡尔曼滤波和 Chan算法结合的定位算法. 利用自适应卡尔曼滤波的参数自我调整的能力， 减少了环境变化和系统偏差所带来的定位误差， 极大程度地提高了定位性能. 实验中利用射频芯片 DW1000 作为脉冲超宽带技术的硬件基础搭建定位系统， 并在空旷环境下进行定位试验. 试验结果表明： 采用自适应卡尔曼滤波后的定位方法相比于传统的定位方法， 具有更高的定位精度和更好的稳定性， 在动态定位中平均偏差可以达到10 cm的误差， 而在静态定位中则可以达到5 cm以内.

参考文献：

[1]刘德亮. 室内环境下无线定位关键技术研究[D]. 天津： 天津大学, 2015.

[2]贺晶晶， 姜平， 冯晓荣. 基于UWB的无人运输车的导航定位算法研究[J]. 电子测量与仪器学报， 2016(11)： 1743-1749.

He Jingjing, Jiang Ping, Feng Xiaorong. Research on navigation and positioning algorithm for unmanned vehicle based on UWB[J]. Journal of Electronic Measurement and Instrumentation, 2016, 30(11)： 1743-1749. (in Chinese)

[3]Gezici S, Tian Z, Giannakis G B, et al. Localization via ultra-wideband radios： a look at positioning aspects for future sensor networks[J].IEEE signal processing magazine, 2005, 22(4)： 70-84.

[4]Shang F, Champagne B, Psaromiligkos I. Joint TOA/AOA estimation of IR-UWB signals in the presence of multiuser interference[Z]. 2014.

[5]Shang F, Champagne B, Psaromiligkos I N. A ML-Based Framework for Joint TOA/AOA Estimation of UWB Pulses in Dense Multipath Environments[J]. IEEE Transactions on Wireless Communications, 2014, 13(10)： 5305-5318.

[6]Hanssens B, Plets D, Tanghe E, et al. An indoor localization technique based on ultra-wideband AoD/AoA/ToA estimation[Z]. 2016.

[7]马丽， 张蕊萍， 杜国璋. 基于 TDOA 的列车无线定位方法研究[J]. 铁道标准设计， 2016, 60(7)： 154-158.

Ma li, Zhang Ruiping, Du Guozhang. Study on TDOA-based wireless train positioning method[J]. Railway Standard Design, 2016, 60(7)： 154-158. (in Chinese)

[8]仲江涛. 基于UWB室内定位算法的研究与实现[D]. 深圳： 深圳大学, 2017.

[9]倪磊磊， 杨露菁， 蔡时超， 等. 基于 TDOA 的 Chan 定位算法仿真研究[J]. 舰船电子工程， 2016, 36(5)： 92-95.

Ni Leilei, Yang Lujing, Cai Shichao, et al. Simulation of Chan positioning algorithm based on TDOA[J]. Ship Electronic Engineering, 36(5)： 92-95. (in Chinese)

[10]Huan L, Bo R. Wireless location for indoor based on UWB[Z]. IEEE, 2015.

[11]Li X, Yang S. The indoor real-time 3D localization algorithm using UWB[Z]. IEEE, 2015.

[12]Xu Y, Shmaliy Y S, Li Y, et al. UWB-based indoor human localization with time-delayed data using EFIR filtering[J]. IEEE Access, 2017(5)： 16676-16683.

[13]王长强， 徐爱功， 隋心. UWB测距的NLOS误差削弱方法[J]. 导航定位学报， 2017(3)： 24-27.

Wang Changqiang, Xu Aigong, Sui Xin. A method of NLOS error inhibition for UWB ranging[J]. Journal of Navigation and Positioning, 2017, 5(3)： 24-27. (in Chinese)

[14]Welch G, Bishop G. An introduction to the Kalman filter[EB/OL]. Dept.Comput.Sci.,Univ. North Carolina, Chapel Hill, Tech. Rep. TR95041, 2006、.

[15]Khan M, Kai Y D, Gul H U. Indoor Wi-Fi positioning algorithm based on combination of Location Fingerprint and Unscented Kalman Filter[Z]. 2017.

[16]孙小文， 张小超， 赵博， 等. 农资仓储脉冲超宽带室内定位系统设计与试验及误差分析[J]. 农业工程学报， 2017(S1)： 23-29.

Sun Xiaowen, Zhang Xiaochao, Zhao Bo, et al. Design, experiment and error analysis of impulse radio-ultra wide band indoor positioning system used in agricultural warehousing[J]. Transactions of the Chinese Society of Agricultural Engineering, 2017(S1)： 23-29. (in Chinese)

[17]Djaja-Josko V, Kolakowski J. A new method for wireless synchronization and TDOA error reduction in UWB positioning system[Z]. 2016.

[18]江凤， 吴飞， 王昌志. 基于CHAN与粒子群算法的协同定位研究[J]. 电子科技. 2017(08)： 1-5.

Jiang Feng, Wu Fei, Wang Changzhi. Research on collaborative localization based on CHAN and particle swarm optimization algorithm[J]. Electronic Science and Technology, 2017(08)： 1-5. (in Chinese)

[19]Liu J, Wu Z, Yin Z. An improved location algorithm in Wireless Sensor Network[Z]. 2013.

[20]朱彩杰. 基于UWB室内定位跟踪算法的对比分析[C]. 中国卫星导航学术年会， 上海： 2017.

[21]赵宏旭， 杨文帅. 基于TDOA的Chan算法和Taylor算法的分析与比较[J]. 电子世界， 2017(9)： 176-177.

Zhao Hongxu, Yang Wenshuai. Analysis and comparison of Chan algorithm and Taylor algorithm based on TDOA[J]. Electronics World, 2017(9)： 176-177. (in Chinese)

[22]王磊， 李鹏涛， 贾宗璞. 基于全质心-Taylor的UWB室内定位算法[J]. 传感器与微系统， 2017(6)： 146-149.

Wang Lei, Li Pengtao, Jia Zongpu. UWB indoor localization algorithm based on full centroid and Taylor[J]. Transducer and Microsystem Technologies, 2017(6)： 146-149. (in Chinese)