空沟对列车运行产生的环境振动隔振效果研究

姚锦宝，夏　禾，胡敬梁

(北京交通大学 土木建筑工程学院，北京　100044)

轨道交通以其客运量大、高速便捷、占地少等优点，在交通运输中起着越来越重要的作用，但是轨道交通也引发了越来越严重的环境振动问题，振害已经成为七大公害之一[1]。对轨道交通引起的环境振动隔振研究已引起了许多学者高度重视。

在以往的轨道交通隔振研究中，针对地表振动问题的研究较多，并且隔振的方式以屏障为主，常见的有空沟、填充沟以及结构隔振屏障等方式。Woods采用模型试验的办法，对空沟隔振进行了研究[2]。Adam等研究空沟对列车运行引起振动的影响时，借助有限元—边界元耦合法进行分析[3]。雷晓燕等研究了空沟尺寸和位置对空沟隔振效果的影响[4]。Jones C对铁路沿线空沟隔振效果进行了测试研究[5]。此外，巴振宁等在层状场地3维精确动力刚度矩阵和层状半空间中移动斜线荷载动力格林函数的基础上，采用移动间接边界元方法对隔振屏障和沉积谷地进行离散求解[6-7]。

瑞利波衰减梯度与体波相比要小得多，在列车引起的土体振动中，衰减较大的往往是体波。研究表明[5]，瑞利波成分占到环境振动的67%，剪切波和压缩波分别占26%和7%。因此，研究空沟对瑞利波隔振的衰减规律更具有实际意义。本文进行空沟对瑞利波隔振效果规律的理论推导，并将空沟隔振对运行列车引起的环境振动影响进行数值分析。

1　空沟对土体振动隔振的理论研究

运行列车引起的振动在土体表面常以瑞利波的形式向远处传播。

1.1　瑞利波的传播

瑞利波的传播有竖向和水平向2个方向，在均匀各向同性的自由半空间中，瑞利波引起的竖向和水平2个方向的位移振幅归一化值[8]可由式(1) 计算。

(1)

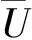
根据参考文献[9]，当拾振点与振源相距较大时，在原点处的集中简谐荷载f(t)=Peiωt(P为幅值、ω为荷载的圆频率)作用下，瑞利波在传播过程中，距荷载距离为r点的竖向位移uz和水平向位移uy分别为

(2)

(3)

其中，

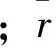
运行列车引起地表上一点的响应可以认为由多个集中简谐荷载叠加而成，需要考虑时间和位置2个因素引起的相位变化，如图1所示。图中d为列车前后轮对距离。

图1　多个竖向简谐荷载叠加

若激振点处作用力的时程曲线呈非周期性变化，可通过快速傅里叶变换转换成一系列周期性集中简谐荷载的组合。

波在传播过程中，在2种介质分界面上会产生反射和透射，如图2所示。图中：I，R和T分别代表入射波、反射波和透射波。

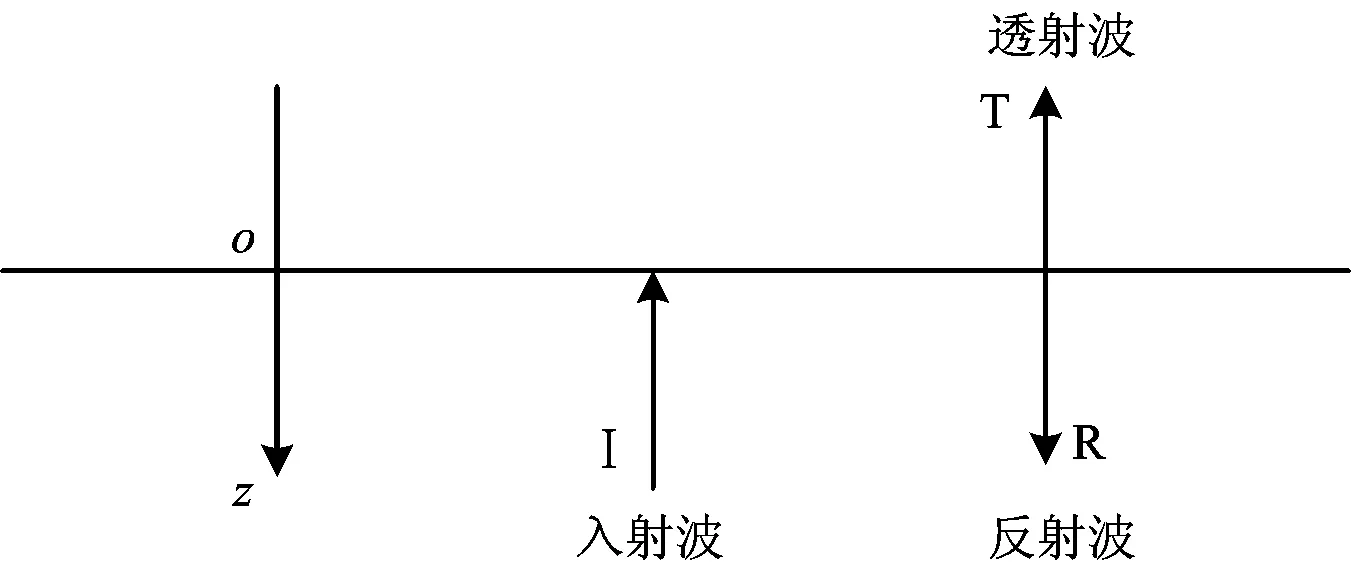
图2　入射波在2种介质分界面处的反射与透射

波的反射和透射系数R和T分别为

(4)

其中，

式中：uI，uR，uT分别为入射波、反射波、透射波的位移；α为阻抗比[10]；ρ2，ρ1，c2，c1，A2和A1分别为入射和投射介质的密度、波速和面积。

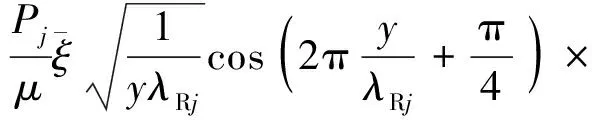
(5)

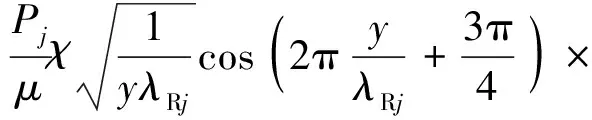
(6)

式中：Pj和θj分别为第j个竖向集中简谐荷载的幅值和相位；λRj和ωj分别为第j个瑞利波的波长和角频率。

1.2　瑞利波沿空沟传播路径及响应

位于远场的空沟的尺寸和位置如图3所示。空沟的截面为矩形，沟深为h，沟宽为w，空沟左侧边缘与振源距离为dR，则沟的截面边缘长度s为2h+w。

图3　位于远场的空沟的尺寸和位置示意图

瑞利波在土体自由表面以下大约1.5倍瑞利波波长范围内随深度快速衰减。远场的瑞利波沿地面及空沟自由表面传播路径及在空沟各转角处的反射与透射如图4所示。

oA段传播的波包括：①来自振源的入射瑞利波I1；②I1经过分界面AB反射后产生的反射波R1。

图4　瑞利波沿地面及空沟传播二维示意图

AB段传播的波包括：①根据分界面的连续条件，I1的透射波T1成为沿空沟AB段往下传播的入射波I2；② I2经分界面BE后产生的反射波R2。

BC段传播的波包括：① I2的透射波T2成为沿BC段传播的入射波I3；② I3经过分界面CF后产生的反射波R3。

CD段传播的波包括：①I3的透射波T3成为沿CD段传播入射波I4；② I4经过分界面DG后产生的反射波R4。

I4的透射波T4沿自由面上DG段传播，形成了空沟外侧土体自由表面的入射波I5。

经推导，o点的简谐荷载在DG段距沟右侧边缘距离为l处的竖向和水平位移为

(7)

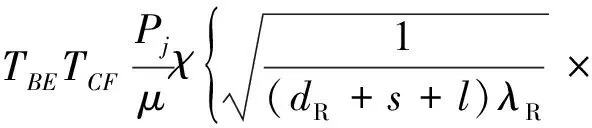
(8)

式中：TBE和TCF分别为空沟底部B和C转角处的透射系数。

由瑞利波沿自由表面的传播规律可知，振动随深度快速衰减；当深度大于1.5倍波长时，式(7)和式(8)中大括号里的第2项与第1项相比可忽略不计。

2　列车—轨道—土体—空沟隔振系统的有限元模型建立

列车—轨道—土体—空沟系统空间动力分析三维模型可分解成列车—轨道和土体—空沟2个二维子系统模型。

2.1　列车—轨道系统模型

列车—轨道系统模型是由车辆模型、轨道模型按照Hertz轮轨接触关系组成的系统。由于列车行进过程中，竖向作用力比横向力要大很多，因此仅考虑竖向作用力。

列车模型中每节车辆均是由车体、转向架、轮对、二系弹簧和阻尼器组成的多自由度振动系统。每个车体和转向架各考虑沉浮和点头2个自由度，每个轮对考虑沉浮1个自由度[11]。

将钢轨、轨枕、道床等参振质量都考虑在轨道系统模型内，用一个3层质量弹簧阻尼器系统表示。

列车—轨道系统二维模型如图5所示。图中:Mci，Jci，Zci和φci分别为第i节车辆质量、点头惯量、沉浮和点头位移；Mti和Jti分别为第i节车辆转向架的质量和点头惯量；Ztij和φtij分别为第i节车辆第j个转向架的沉浮和点头位移；kti和cti分别为第i节车辆二系悬挂弹簧刚度和阻尼系数；kwi和cwi分别为第i节车辆的一系悬挂弹簧刚度和阻尼系数；Mwi和zwij分别为第i节车辆轮对质量和第i节

图5　列车—轨道系统模型

车辆第j个轮对的沉浮位移；c1，c2，c3，m1，m2，m3，k1，k2和k3分别为轨道系统3层质量弹簧阻尼器的阻尼、质量和刚度。

单根钢轨的质量线密度取61.22 kg·m-1，弹性模量取30 G·m-2，单根钢轨绕垂直钢轨走向的水平轴截面惯性矩取4×10-5m4。

2.2　土体—空沟系统模型

土体—空沟系统模型的基底为固定约束，侧边界为线弹性约束，其刚度根据土层的特性选取。由于轨道交通系统引起土体的振动振幅不大，可近似假定地基土为线弹性体材料。模型沿轨道方向长度取120 m，与轨道中心线垂直的水平方向长度取80 m，深度取20 m，如图6所示。

图6　土体—空沟系统二维平面模型

将土体视为均匀半空间，故土层选用1种材料，其弹性模量取35 MN·m-2，质量密度取1 800 kg·m-3，泊松比取0.4，阻尼比取0.1。

3　空沟隔振数值分析

数值分析选取南京轻轨列车以速度90 km·h-1运行时在地基表面产生的竖向动荷载作为激励荷载，南京地铁列车参数见文献[12]，利用列车—轨道系统模型计算得到的竖向动荷载时程曲线，如图7所示。

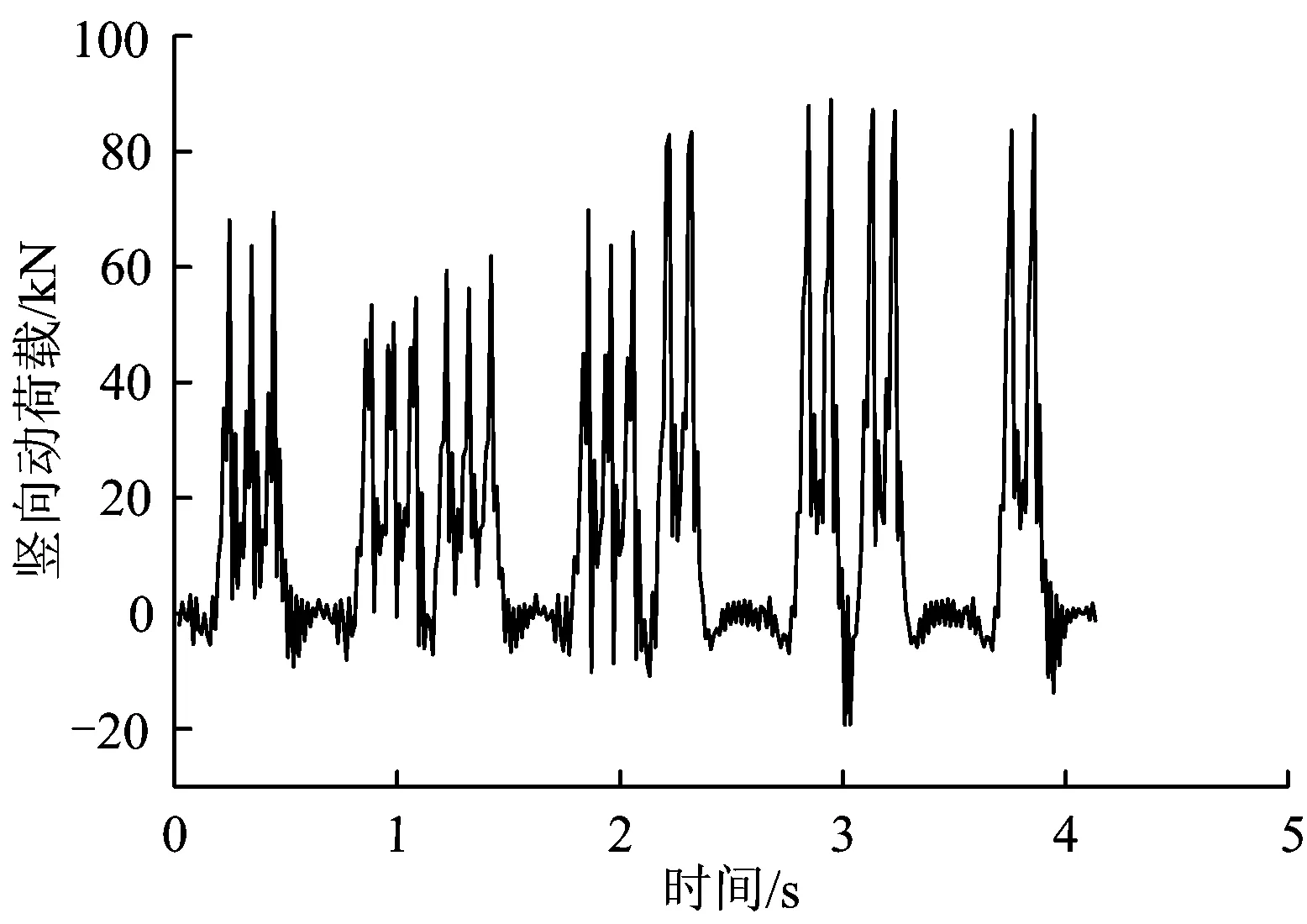
图7　竖向动荷载时程曲线

改变空沟的深度、宽度、与振源的位置以及拾振点距空沟右侧边缘距离等参数，进行运行列车引起的土体振动规律数值分析。

3.1 空沟深度的影响

取空沟宽1 m，动荷载加载点距空沟左侧边缘25 m，空沟深度分别取0，1，2，3，4，6和8 m，进行运行列车引起的土体振矾数值分析。图8为距空沟右侧边缘2 m位置处地表拾振点的水平向和竖向加速度频谱随空沟深度的变化图。

图8距空沟右侧边缘2 m处地表拾振点加速度频谱随空沟深度的变化图

从图8可以看出：随沟深增加，水平向及竖向振动的隔振效果均越明显；空沟对高频11～40 Hz的隔振效果较低频1～10 Hz的隔振效果明显；空沟隔振效果与瑞利波波长有关，大于瑞利波长时，隔振效果较好。

3.2　空沟宽度的影响

取空沟深4 m，动荷载加载点距空沟左侧边缘25 m，空沟宽度分别取0.5，1，1.5和2 m，进行运行列车引起的土体振动数值分析。图9为距空沟右侧边缘2 m位置处地表拾振点的水平向及竖向加速度频谱随空沟宽度的变化图。

从图9可以看出：空沟宽度的变化对高频11～40 Hz和低频1～10 Hz振动的隔振效果均不明显；空沟宽度的变化对水平向振动的隔振效果比竖向振动明显。

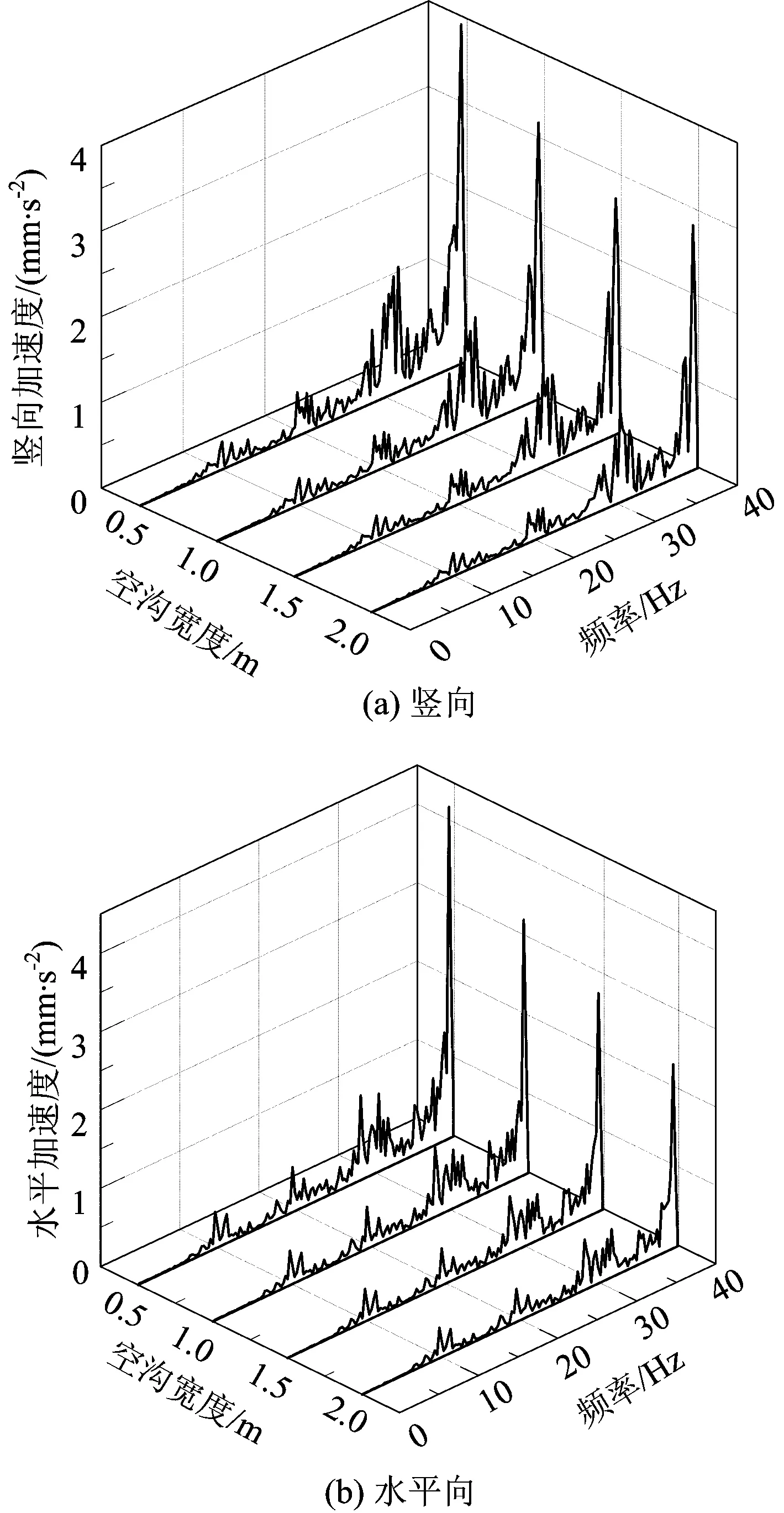
图9距空沟右侧边缘2 m处地表拾振点加速度频谱随空沟宽度的变化图

3.3　动荷载加载点距空沟左侧边缘距离的影响

取空沟宽度1 m、空沟深度4 m，动荷载加载点距空沟左侧边缘距离分别取16，20，24和28 m，进行运行列车引起的土体振动数值分析。图10为距加载点32 m位置处地表拾振点的水平向及竖向加速度频谱随动荷载加载点距离的变化图。

从图10可以看出：加载点距空沟左侧边缘距离的增加，水平向和竖向振动的隔振效果均不明显;加载点距空沟左侧边缘距离的增加，高频11～40 Hz振动的隔振效果比低振1～10 Hz振动明显。

3.4　拾振点距空沟右侧边缘距离的影响

取空沟宽度1 m、空沟深度4 m，动荷载加载点距空沟左侧边缘距离25 m，拾振点距空沟右侧边缘距离分别取4，6，8和10 m，进行运行列车引起的土体振动数值分析。图11为距空沟右侧边缘不同距离地表拾振点水平向及竖向加速度频谱的变化图。

图10距加载点32 m处地表拾振点加速度频谱随动荷载加载点距离变化图

图11距沟右侧边缘不同距离地表拾振点的加速度频谱图

从图11可以看出：随与距沟右侧边缘距离增大时，振动总趋势是降低的，水平向振动的降低值比竖向大。由于土体表面发生反射，在空沟外侧边缘附近区域会出现振动加强现象。

4　理论公式验证

为验证本文推导公式的有效性，选取仿真分析的空沟深度变化和拾振点距空沟右侧边缘距离变化工况用理论公式进行计算，将其计算结果与仿真结果进行对比。

图12为图7的列车激励荷载经过快速傅里叶变换(FFT)后，叠加得到时程曲线。将其代入式(7)，得到拾振点的振动响应时程曲线。

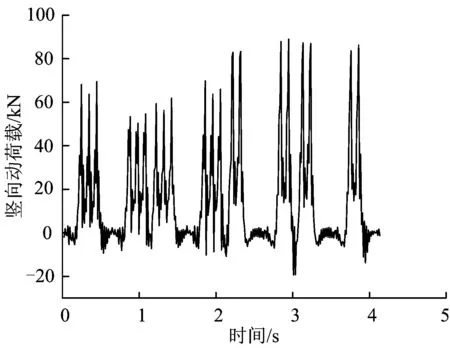
图12FFT变换后竖向动荷载时程曲线(v=90 km·h-1)

对比图7与图12发现，用于理论计算的经过FFT变换得到的激励荷载与用于数值分析输入的激励荷载相差较小。

图13给出了空沟宽1 m，动荷载加载点距空沟左侧边缘25 m，空沟深度分别为1，2，3，4，6和8 m时，由式(7)计算和数值分析得到的距空沟右侧边缘2 m处地表拾振点的竖向加速度频谱。

图14给出了空沟宽1 m，空沟深度4 m，动荷载加载点距空沟左侧边缘25 m，拾振点距空沟右侧边缘距离分别为4，6，8和10 m时，由式(7)计算和数值分析得到的地表拾振点的竖向加速度频谱。

从图13和图14中可以看出：公式计算和数值分析得到的地表拾振点的加速度均随着沟深的增加而减小，随拾振点距沟右侧边缘距离增大，竖向振动均有降低趋势，公式计算与数值分析结果的变化规律基本一致；理论计算与数值分析结果的量级相同，但由于理论计算时，振动响应叠加时是相互独立的，理论计算略高出数值分析结果。

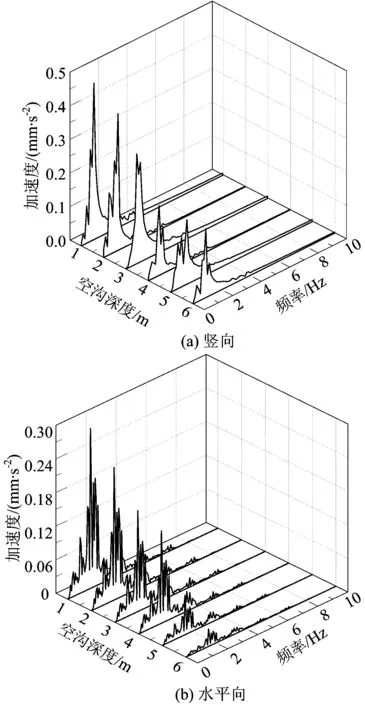
图13公式计算和数值分析得到的距空沟右侧边缘2 m处地表拾振点加速度频谱随空沟深度变化对比图

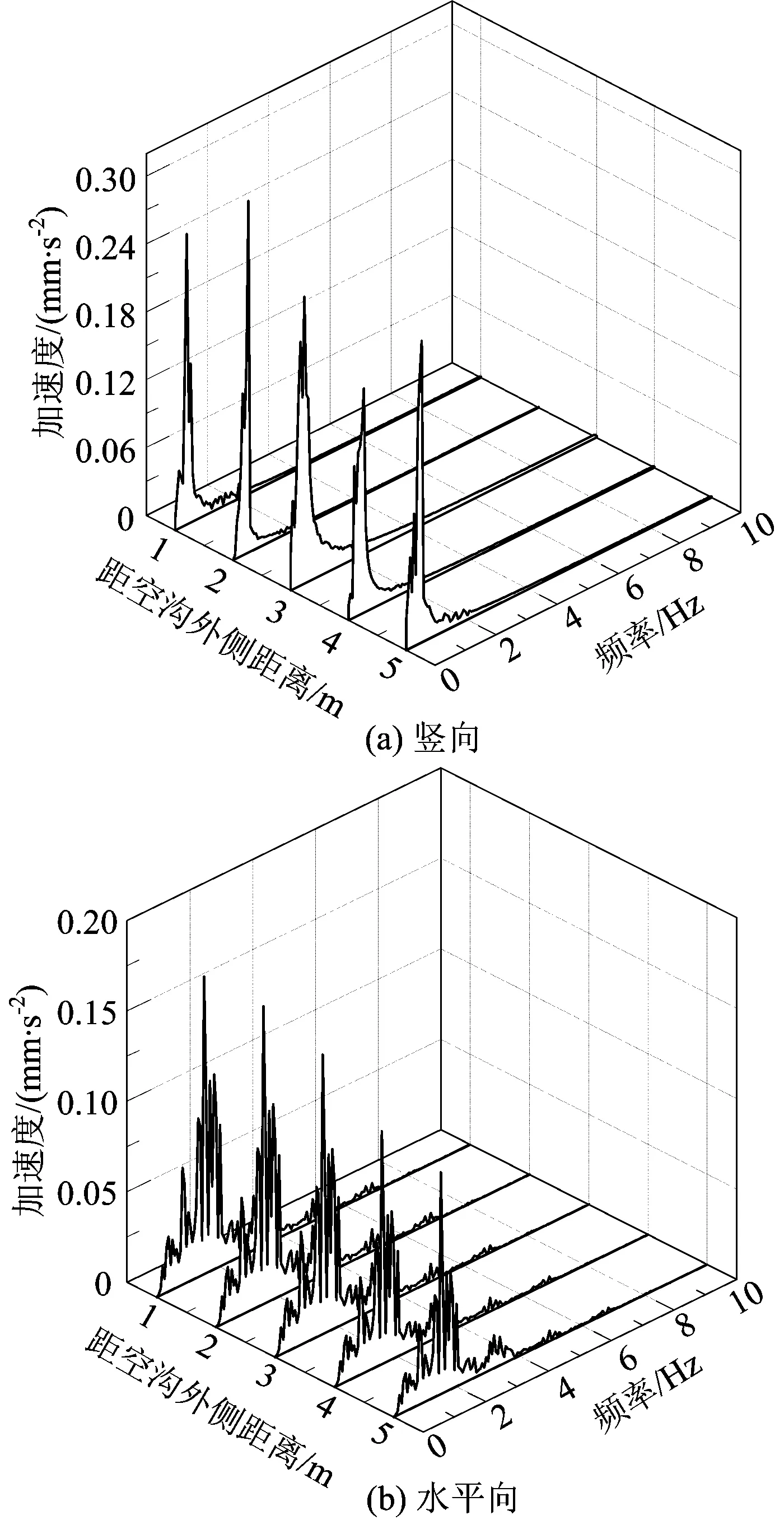
图14公式计算和数值分析得到的距沟右侧边缘不同距离地表拾振点的加速度频谱对比

5　结　论

(1) 理论公式计算结果与数值分析计算结果基本一致，表明本文理论推导的公式可以用于分析空沟对运行列车引起的环境振动影响。

(2) 随着空沟深度的增大，隔振效果均越明显；空沟对高频11～40 Hz的隔振效果比低频1～10 Hz明显。

(3) 空沟隔振效果与瑞利波波长有关，沟深大于瑞利敞长时，隔振效果较好。

(4) 空沟宽度、空沟位置以及拾振点距沟外侧的距离对隔振效果均不明显，但对水平向的隔振效果比竖向好。

[1]夏禾,曹艳梅.轨道交通引起的环境振动问题[J].铁道科学与工程学报,2004,1(1): 44-51.

(XIA He, CAO Yanmei. Problem of Railway Traffic Induced Vibrations of Environments [J]. Journal of Railway Science and Engineering, 2004, 1(1): 44-51. in Chinese)

[2]WOODS R D. Screening of Surface Waves in Soils [J].Journal of the Soil Mechanics and Foundations Division, ASCE,1968, 94(4):951-979.

[3]ADAM M, ESTORFF O V. Reduction of Train-Induced Building Vibrations by Using Open and Filled Trenches [J]. Computers and Structures, 2005,83(1):11-24.

[4]侯德军,雷晓燕,罗信伟. 铁路隔振沟减振的数值分析[J].铁道科学与工程学报,2006,3(2):48-52.

(HOU Dejun, LEI Xiaoyan. LUO Xinwei.The Numerical Analysis of Railway Vibration Reduction by Trenches[J].Journal of Railway Science and Engineering, 2006, 3(2): 48-52. in Chinese)

[5]THOMPSON D. Railway Noise and Vibration:Mechanisms,Modelling and Means of Control[M].Amsterdam:Elsevier Science, 2009:399-435.

[6]巴振宁,梁建文,金威.高速移动列车荷载作用下成层地基—轨道耦合系统的动力响应[J].土木工程学报,2014,47(11): 108-119.

(BA Zhenning, LIANG Jianwen, JIN Wei. Dynamic Responses of Layered Ground-Track Coupled System under the Moving Loads from High-Speed Train[J]. China Civil Engineering Journal, 2014, 47(11): 108-119. in Chinese)

[7]梁建文,巴振宁.三维层状场地的精确动力刚度矩阵及格林函数[J].地震工程与工程振动,2007,27(5):7-17.

(LIANG Jianwen,BA Zhenning. Exact Dynamic Stiffness Matrices of 3-D Layered Site and Its Green’s Functions[J].Journal of Earthquake Engineering and Engineering Vibration, 2007, 27(5): 7-17. in Chinese)

[8]杨天春,陈永贵.瑞利波勘探中波长深度转换系数的探讨[J].勘察科学技术,2008(2):26-30.

(YANG Tianchun,CHEN Yonggui. Discussion about the Wavelength-Depth Conversion Coefficient in Rayleigh Wave Exploration[J]. Investigation Science and Technology, 2008(2): 26-30. in Chinese)

[9]柴华友,吴慧明,张电吉，等.弹性介质中表面波理论及其在岩土工程中应用[M].北京:科学出版社,2008.

[10]黎在良,刘殿魁.固体中的波[M].北京:科学出版社,1998.

[11]夏禾，张楠.车辆与结构动力相互作用[M].2版.北京:科学出版社,2005.

[12]姚锦宝，夏禾，陈建国，等.列车运行引起高层建筑物振动分析[J].中国铁道科学，2009,30(2):71-76.

(YAO Jinbao,XIA He，CHEN Jianguo， et al. Numerical Analysis on the High-Rise Building Vibrations Induced by Moving Trains[J].China Railway Science, 2009,30(2):71-76. in Chinese)

[13]刘奉喜，刘建坤，防建宏,等.多年冻土区铁路隔振沟隔振效果的数值分析[J].中国铁道科学，2003,24(5):48-51.

(LIU Fengxi,LIU Jiankun，FANG Jianhong，et al. Numerical Analysis of the Vibration Isolation Effect of the Railway Vibration Isolating Cutting in Permafrost [J].China Railway Science, 2003,24(5):48-51. in Chinese)

[14]陈昆,贾霄，刘彬，等.高速铁路空沟隔振措施隔振效果的有限元分析[J].地震工程学报，2014,36(3):575-579.

(CHEN Kun, JIA Xiao，LIU Bin，et al. Finite Element Analysis of Reducing the High-Speed Railway Vibration Effect on the Environment Using Open Trenches [J].China Earthquake Engineering Journal, 2014,36(3):575-579. in Chinese)