考虑动态客流需求和大小交路模式的城市轨道交通列车开行方案优化

代存杰，李引珍，展宗思，柴　获

(1.兰州交通大学 机电技术研究所，甘肃 兰州　730070；2.兰州交通大学 交通运输学院，甘肃 兰州　730070；3.西安市地下铁道有限责任公司，陕西 西安　710016)

列车开行方案是城市轨道交通运营组织的重要工作，列车发车时刻表是开行方案设计的核心内容，需要根据客流需求的分布特征科学制订。由于列车运行路线上存在区段客流不均衡、客流断面突变现象，因此应基于不同的列车交路模式，设计合理的列车发车时刻表，对列车开行方案进行优化，以减少乘客等待时间、提高列车满载率。

国内外学者在列车发车时刻表优化方面做了诸多研究，Serafini等[1]建立了时间约束下周期性事件调度模型，并应用于列车发车时刻表的设计；Kwan等[2]考虑列车运营费用和乘客满意度，利用启发式算法对列车发车时刻表进行优化；Liebchen[3]在既有图解模型的基础上对柏林地铁系统的列车发车周期进行了优化；Kroon等[4]通过调整列车运行的补偿时间和相邻列车之间的缓冲时间，提高列车发车时刻表在随机扰动下的鲁棒性；廖勇[5]将客流到达车站的过程视为随机过程，据此对城际列车发车间隔进行优化。

在城市轨道交通的实际运营过程中，不同时段内不同车站的乘客到站数量存在差异，致使客流需求存在时间和空间上的不均衡性。若乘客到站数量服从均匀分布或泊松分布，则周期性的发车间隔时间可减少乘客等待时间[6]。在具有时变特征的客流需求下，固定发车间隔时间会导致部分乘客的等待时间过长[7]。

根据客流需求在时间上分布不均衡的特征，Cury等[8]以乘客满意度和列车运营成本为目标建立模型，得到非固定的列车发车间隔时间；Albrecht[9]根据列车运力确定最优发车频率后，设计了面向乘客需求的列车发车时刻表；Niu等[10]考虑拥挤情况下的客流时变特征，建立城市轨道交通列车发车时刻表的优化模型；Barrena等[11]以乘客平均等待时间最小为目标，对动态客流需求下的列车发车时刻表优化；Hassannayebi等[12]考虑客流需求和列车行程时间的不确定性，设计了两阶段模拟方法以生成鲁棒的列车发车时刻表。

针对客流需求空间分布的不均衡性，常采用不同的列车开行方案以适应客流空间分布特征[13]；程婕等[14]以列车输送能力与客流空间分布的最佳匹配为原则，建立了列车开行方案优化的多目标0-1规划模型；王媛媛等[15]以乘客出行成本及企业运营成本最小为目标，构建大小交路模式下列车开行方案的优化模型；凌俊等[16]根据城市轨道交通客流不均衡情况，对非高峰期列车开行方案进行研究。

但是，这些既有研究多从单一方面对城市轨道交通列车开行方案进行优化，没有同时考虑客流需求的时间和空间分布不均衡特征以及列车交路模式。为此，本文考虑客流需求的时间和空间分布特征，对大小交路模式下列车开行方案优化进行研究。

1　问题描述

1.1　动态客流需求分析

动态客流需求分析的核心工作是分析客流需求的时间和空间分布规律。影响客流在时间上变化的主要因素为乘客的出行行为，乘客的日常出行行为在1天内是不同的，导致1天内客流是动态变化的，但在1天内的出行行为又具有一定的规律性，所以，同一车站各时段内的客流密度基本是确定的，不同车站的客流变化规律不同。

影响客流在空间上变化的主要因素是车站覆盖的客流集散点的规模和数量不同，因而各车站的乘降人数不同，致使各断面客流空间分布的不平衡；同时，新的居民住宅区入住和新的轨道交通线路投入运营，也会使车站乘降人数发生较大的变化。

为表达不同时段内的动态客流需求特征，定义如下参数：U={1,2,…,2N}为车站序号集合，其中1,2,…,N为上行方向车站编号，N+1,N+2,…,2N为下行方向车站编号，且车站1与2N；2与2N-1；…；N与N+1分别共用同一个站台；T为城市轨道交通日运营时间长度，δ为单位时间，列车发车时间点t∈T，且t=nδ，n为正整数；u∈U和v∈U为单个车站的编号，且v>u；ρu,v(t)为时间点t从u出发前往v的客流密度，当u∈{1,2,…,N}且v∈{N+1,N+2,…,2N}时，ρu,v(t)=0；Πu,v(t)为列车开始运营时间点0到时间点t之间从u出发前往v的累计客流需求。

Πu,v(t)与ρu,v(t)的关系表达式为

(1)

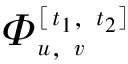
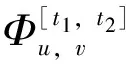
(2)

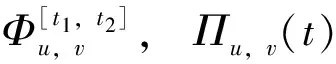
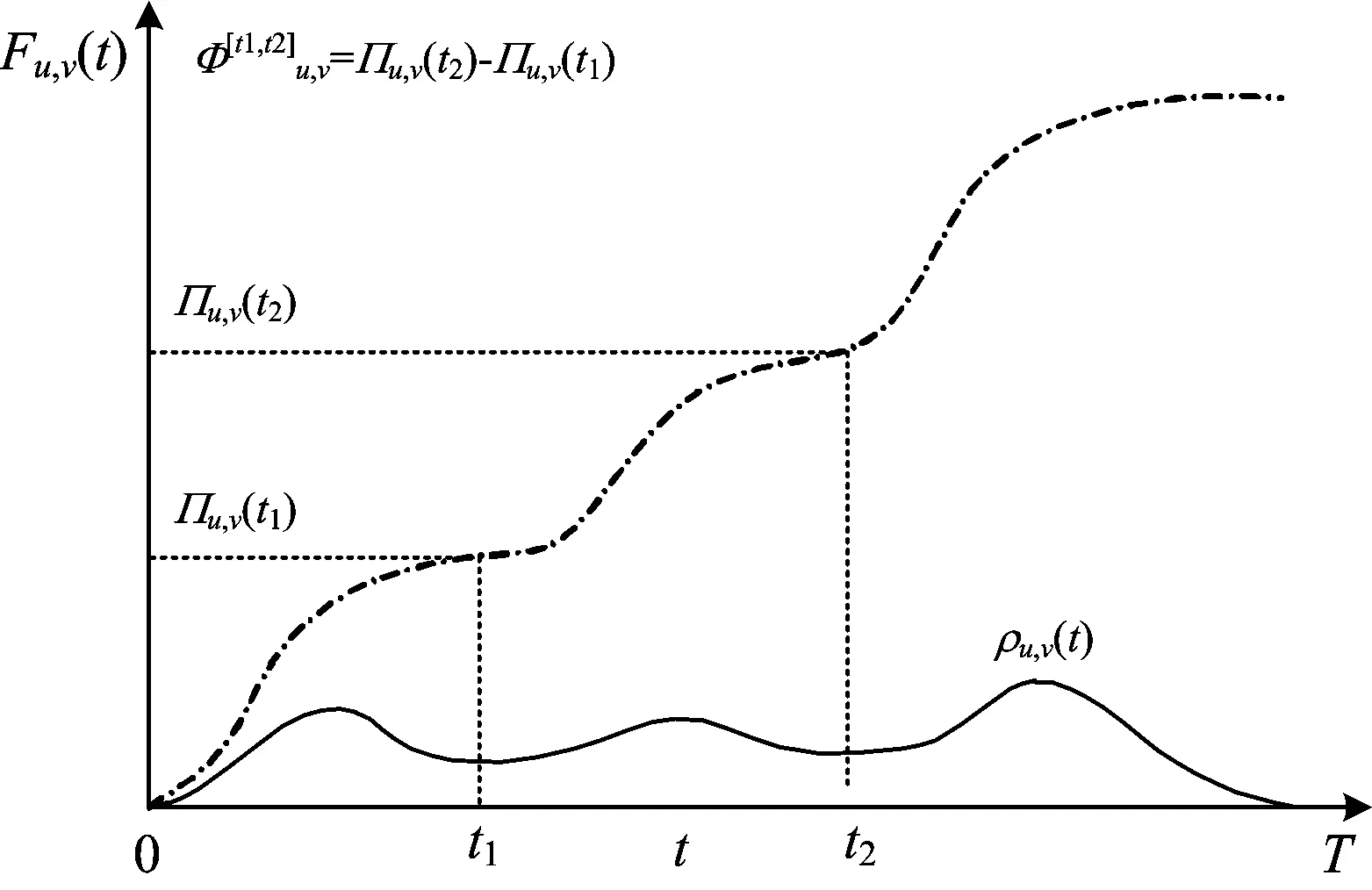
图1　车站u的累计客流需求

(3)

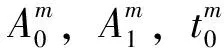
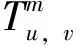
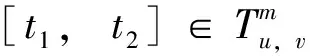
(4)

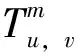
(5)

对式(5)求和可得时段[t1,t2]内从车站u出发的累计客流需求为

(6)

1.2　大小交路模式列车发车时间间隔分析

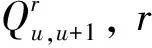
在大小交路模式下确定列车开行方案时，为避免列车在线路中的行车冲突，通常取固定发车间隔时间，不同交路列车的开行数量为严格的倍数关系，但这种固定发车间隔时间会导致客流需求低峰期时的运力浪费或客流需求高峰期时的运力不足[18]。在列车运行控制技术可行的前提下，大小交路列车的开行只要满足最大、最小追踪间隔约束，可根据客流需求特征动态设定非固定的发车间隔时间[20]，使列车交路方案确定的输送能力与客流需求空间特征达到最佳匹配。

2　多目标优化模型

2.1　假设条件

根据城市轨道交通实际运营情况首先作如下假设：①各站乘客服从“先到先服务”的原则；② 乘客不选择列车交路类型，即可能登乘时则登乘；③列车在各站停靠时间和站间行驶时间是确定的；④不存在列车越行和会让的情况。

2.2　参数定义

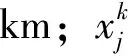
2.3　模型建立

根据假设条件和相关参数定义，计算模型的相关参数，具体如下。

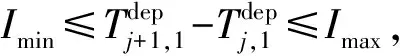
(7)

列车j从车站u的出发时间为

(8)

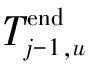
(9)

当车站u无滞站乘客存在时，可成功登乘列车j的乘客数量γj,u为

(10)

(11)

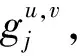
(12)

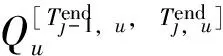
γj,u=A-(Cj-u-1-Oj,u)

(13)

此时，部分乘客需要等待列车j+1，则Bj,u为

Bj,u=Wj,u-γj,u

(14)

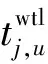
(15)

当列车为小交路运行时，列车需要在车站u′清客，则该部分乘客在车站u′的等待时间为

(16)

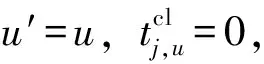
(17)

在整个日运营时间长度T内，根据式(6)可得车站u的累计客流需求为

(18)

由此可计算所有乘客的平均等待时间ћ，即

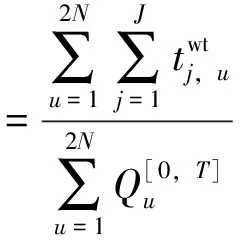
(19)

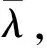
(20)

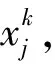
(21)

考虑客流需求的动态特征和大小交路模式特点，以减少乘客平均等待时间、提高列车平均满载率、减少列车总走行公里数为优化目标，建立城市轨道交通列车开行方案的多目标混合整数非线性优化模型为

(22)

s.t.

(23)

(24)

(25)

(26)

(27)

约束条件中：式(23)和式(24)分别为最小和最大发车间隔时间分别满足最小和最大追踪列车间隔时间约束；式(25)为车辆运力供需比约束，即开行列车的输送能力不小于客流需求量；式(26)和式(27)分别为列车j与相邻列车j-1和j+1在车站u′的追踪列车间隔时间不小于最小追踪列车间隔时间Imin，以保证小交路运行的列车j在折返站u′折返后的运行安全。

3　求解算法设计

在对模型求解时，需要根据客流特征动态安排列车的交路模式和发车时间，此问题属于组合优化问题，可用遗传算法有效地求解[10]。由于各求解目标并不统一，只能根据各目标的优化准则得到非支配解。因此，本文将快速非支配遗传算法NSGA-Ⅱ与自适应邻域搜索方法相结合对模型求解，并对遗传操作中的交叉和变异算子进行改进。

NSGA-Ⅱ为多目标进化算法，降低了非支配排序遗传算法的复杂性，具有运行速度快、收敛性好的优点，成为其他多目标优化算法的基准[21]。本文在标准NSGA-Ⅱ的基础上，设计多点动态交叉操作，并结合启发式邻域搜索机制，对染色体的变异操作进行改进，以产生性能更优的新染色体，加快算法的求解速度。

3.1　编码设计

考虑列车发车时间的离散性，对染色体采用0-1编码方式。染色体中的每个基因表示时段T内的单位时间点，对应编码0或1。基因值为1表示该时间点有列车出发，基因值为0表示在对应时间点无列车出发。设间隔时间基准δ=1(min)，Imin=3δ，Imax=10δ，染色体结构如图2所示。

二进制编码可表示单一交路模式的列车离散发车间隔时间，为适应大小交路模式，在设计染色体编码时需要考虑交路类型。在染色体的基因信息中加入开行列车的交路模式，0表示该时刻没有列车发出，1表示该时刻有交路类型1的列车发出，2表示该时刻有交路类型2的列车发出。大小交路模式的染色体结构在图2的基础上变为如图3所示。

图2　染色体结构

图3　大小交路模式的染色体结构

3.2　选择操作

针对染色体种群，利用快速非支配排序策略计算每条染色体的层级序号r(·)和拥挤距离d(·)。 根据r(·)和d(·)可以比较2条染色体的优劣。将染色体x1和染色体x2进行比较，如果x1优于x2，则x1至少满足下面2种条件之一：①r(x1)>r(x2)； ②r(x1)=r(x2),d(x1)>d(x2)。

3.3　交叉算子设计

在传统单点交叉的基础上，设计动态多点交叉操作。虽然这种交叉方式可能会破坏优秀染色体的结构，但会提高算法对整个解空间的搜索能力，比单点交叉表现出更好的收敛性能[22]。

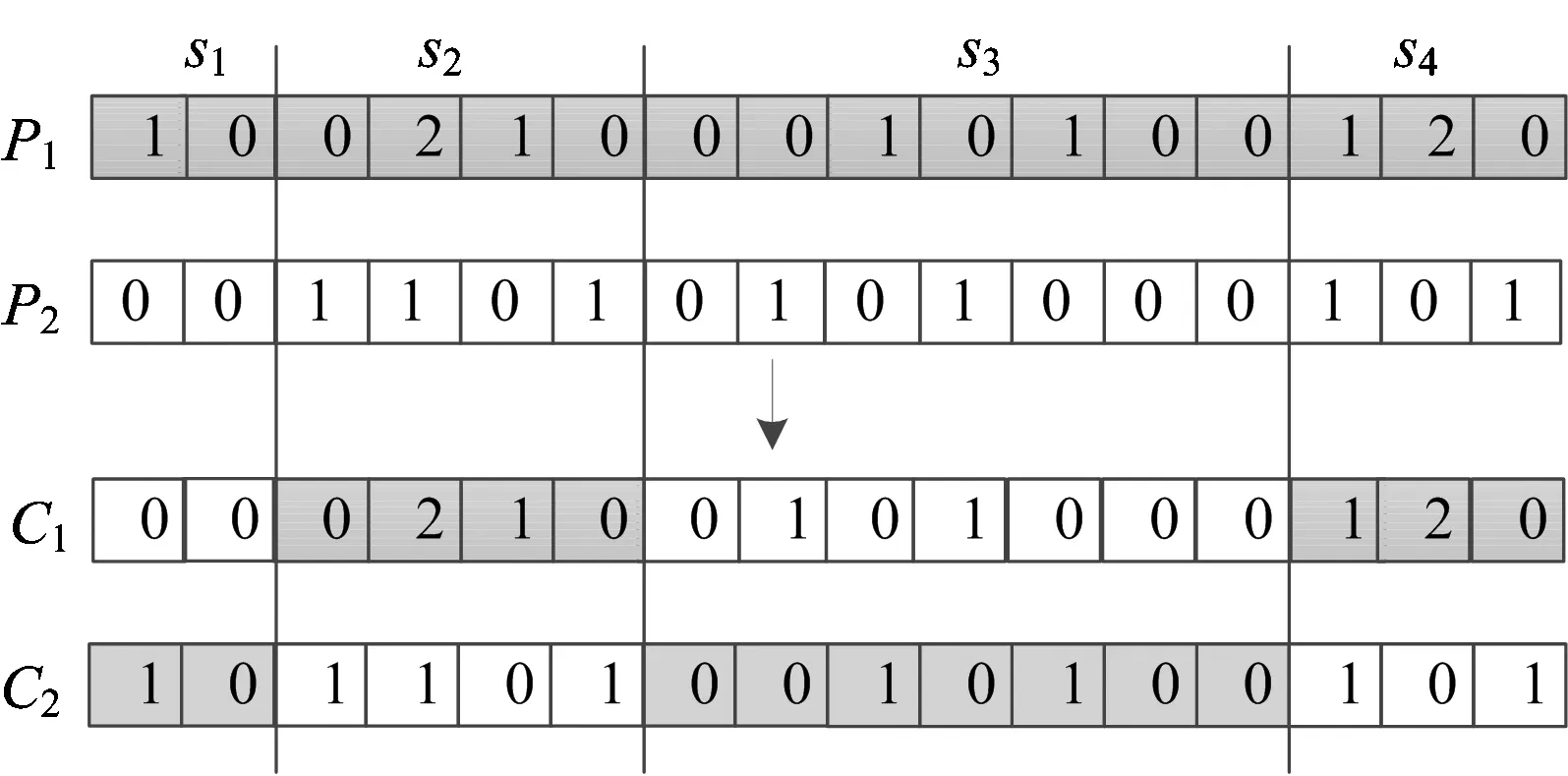
图4　动态多点交叉操作

在交叉操作后，只保留满足约束条件的子代染色体。将可行子代染色体放入新的种群，用来与父代染色体所在种群进行非支配比较，达到精英保留和种群优化的目的。

3.4　变异算子设计

在设计染色体变异算子时，结合自适应邻域搜索机制对染色体进行启发式变异，分为染色体破坏操作和染色体修复操作。

1)染色体破坏操作

破坏操作是用来减少开行的列车数量或将列车由大交路运行模式变为小交路运行模式，以提高列车的满载率，避免运力过剩，同时减少列车走行公里数。操作步骤如下。

2)染色体修复操作

修复操作是用于增加开行列车数量，或根据折返站前后连续客流断面的平均值，进行列车大小交路调整，以减少乘客的等待时间。操作步骤如下。

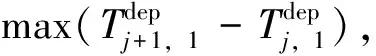
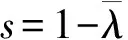
4　算例及结果分析

以西安地铁2号线为研究对象，此线路共设有21座车站，北客站至韦曲南站为方向上行。列车在各区间的运行时间、在各站的停靠时间见表1。

韦曲南站的停留时间为大交路列车在该站进行折返作业时间，会展中心站的停留时间分别为小交路列车的折返作业时间和大交路列车的停靠时间。大交路列车的走行公里数为L2=53.0 km，小交路列车的走行公里数为L1=39.8 km，日运营时间为06:10至23:15，即T=1 025 min。

地铁2号线的运营车辆采用B型车、3动3拖6辆编组方式，列车定员为1 468人，终点站均采用站后折返；北客站最小全折返时间为5.7 min，韦曲南站最小全折返时间为4.3 min。最小追踪列车间隔时间Imin=3 min，最大追踪列车间隔时间为Imax=10 min，大交路的运营周期时间为104.0 min，小交路的运营周期时间为82.6 min。

根据地铁自动售检票系统，可得到某日运营时间内地铁2号线各站累计到达客流需求变化曲线(以30 min为时间粒度提取)，如图5所示。

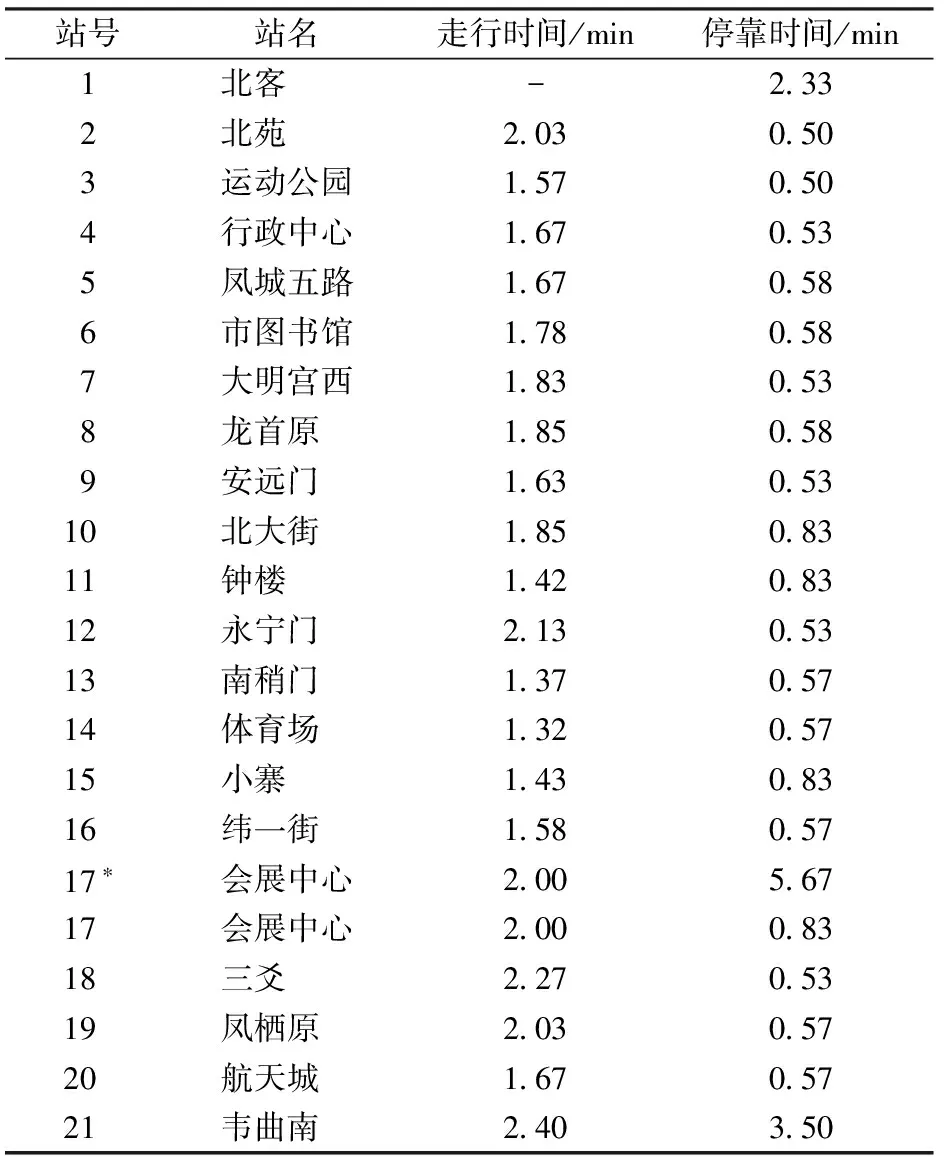
表1　列车站间运行时间和各站停靠时间

*为小交路折返站

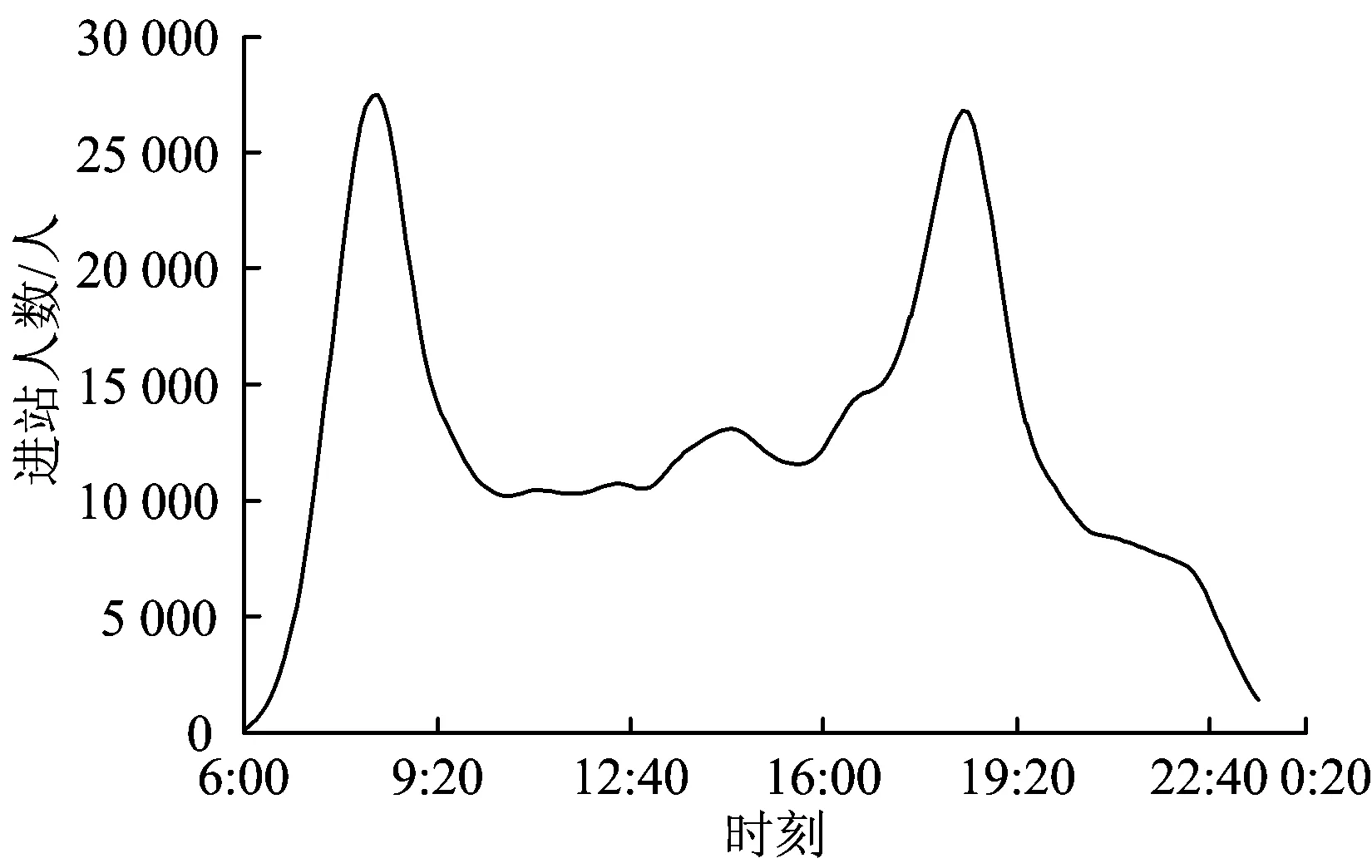
图5　累计到达客流需求变化曲线

设置染色体的种群规模为200，最大迭代次数为300，交叉概率为0.8，动态交叉点个数为5，变异概率为0.15。取ε=0.2；当s>ε时，d=rand(30,50)，m=rand(20,30)； 当s≤ε时，m=rand(30,50)，d=rand(20,30)。经过计算，可得到大小交路模式下列车发车时间优化结果。在生成的非支配解集中，解的空间分布如图6所示。

在非支配解集中，取各个目标函数的最优值时，对应的列车开行方案见表2。

解析非支配解集中的任一非支配解，都可得到列车在始发站出发时刻及对应的列车运行图。以解集中的非极值解(3.26,85.53%,8.63)为例，对应的开行列车总数为170列，其中大交路开行列车总数为142列，小交开行路列总数为28列，在u=1的列车发车时刻及运行情况如图7所示。

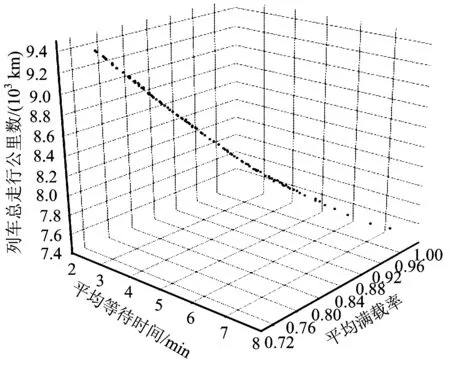
图6　非支配解的空间分布图

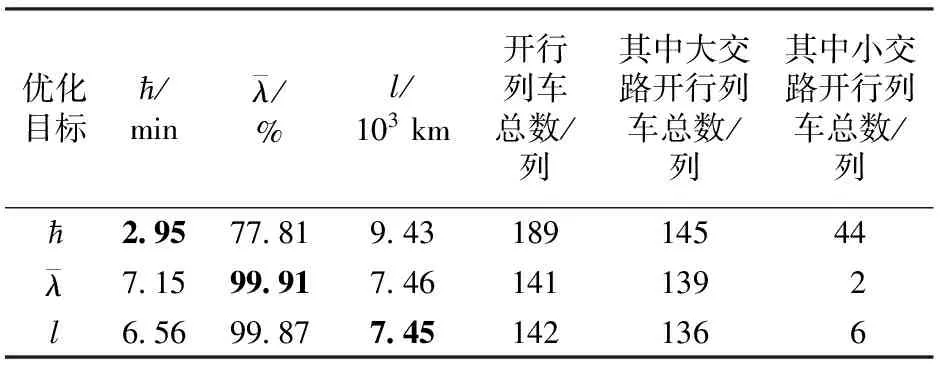
优化目标ћ/min λ/%l/103km开行列车总数/列其中大交路开行列车总数/列其中小交路开行列车总数/列ћ2 9577 819 4318914544 λ7 1599 917 461411392l6 5699 877 451421366

图7　列车发车时刻及运行图

分析图5和图7可知：列车开行方案中发车间隔时间的大小与客流需求的变化是吻合的，如早高峰和晚高峰时段，客流量较大，则列车发车间隔时间较小，并且同时开行大、小交路列车；在平峰或低峰时段，客流量较小，则列车发车间隔时间较大，且仅开行大交路列车。

将大小交路模式下的列车开行方案设置为固定追踪列车间隔时间，并设最小追踪列车间隔时间Imin=5 min，最大追踪列车间隔时间为Imax=10 min。对模型求解后生成非支配解集，当各目标函数分别取最优值时，得到固定追踪列车间隔时间条件下的开行方案见表3。

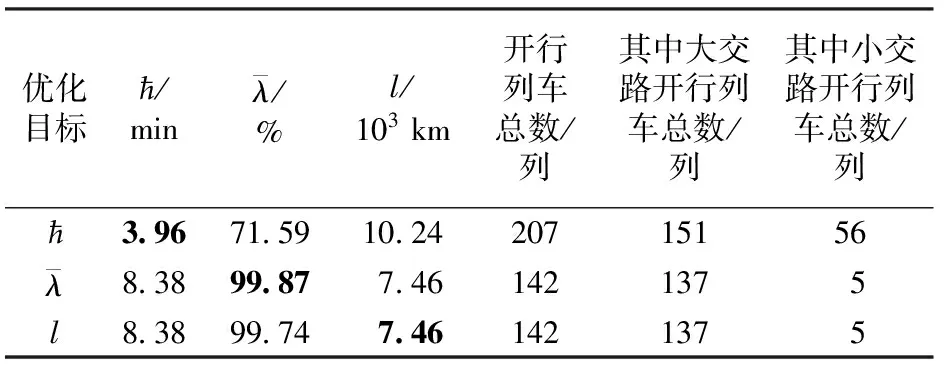
表3　固定追踪列车间隔时间的列车开行方案参数

对比表2和表3可知：固定追踪列车间隔时间与非固定追踪列车间隔时间条件下对各优化目标取极值时，乘客平均等待时间增加34.24%，列车平均满载率降低0.04%，列车总走行公里数提高0.13%。因此，根据客流的动态需求采用非固定列车追踪间隔时间，可以降低乘客的平均等待时间，减小列车开行总数，从而更好地满足乘客和运营企业双方的利益。

为了分析列车在大小交路模式与单一大交路模式下的运行方案差异，使用相同的客流数据和遗传操作参数，得到单一大交路模式下列车运行数据的非支配解。为使数据具有可比性，分别在生成的非支配解集中取近似相同的列车平均满载率，计算不同模式下乘客平均等待时间、列车总走行公里数和开行列车总数。并将其与大小交路模式下的结果进行对比，见表4和表5。

表4　单一大交路模式下不同时的列车开行方案参数

表5　大小交路模式下不同时的列车开行方案参数

注：()内为大交路开行列车总数

由表4和表5可知：当开行列车的平均满载率近似相等时，大小交路模式列车开行方案要明显优于单一大交路模式的列车开行方案；在开行列车总数相差无几的情况下，单一大交路模式下的乘客平均等待时间远高于大小交路模式下乘客平均等待时间。从计算过程的中间数据可知，在客流高峰时段，由于区段客流断面的分布不均，单一大交路模式下共线路段的滞站乘客数量较大，致使乘客等待时间的增加。因此，考虑乘客出行需求的时间依赖特征，以及客流断面分布不均的空间特征，开行大小交路模式列车，能够同时减少乘客等待时间和列车总走行公里数。

5　结　论

(1)通过分析乘客出行需求的时间、空间分布特征，采用4参数Logistic函数对累计客流曲线分段拟合，推导出各车站在任意时间段内客流需求量的计算公式。

(2)考虑运营企业和乘客双方的不同需求，以最大、最小追踪列车间隔时间和运力供需比为约束条件，以所有乘客平均等待时间最小、列车平均载客率最高、列车总走行公里最少为目标函数，建立城市轨道交通列车开行方案的多目标混合整数非线性优化模型；结合自适应邻域搜索策略，设计改进的NSGA-Ⅱ算法对模型求解，并根据大小交路模式的列车发车特点，设计特殊结构的编码方式。

(3)以西安地铁2号线某工作日的客流数据为例，对列车开行方案进行了优化。结果表明，根据动态客流需求对大小路模式下的列车开行方案优化，可有效减少乘客的平均等待时间，提高列车平均满载率并减少列车总走行公里数，从而更好地满足乘客和运营企业双方利益诉求。

[1]SERAFINI P, UKOVICH W. A Mathematical Model for Periodic Scheduling Problems [J]. Siam Journal on Discrete Mathematics, 1989, 2(4):550-581.

[2]KWAN C M, CHANG C S. Application of Evolutionary Algorithm on a Transportation Scheduling Problem: the Mass Rapid Transit[C]//The 2005 IEEE Congress on Evolutionary Computation. Edinburgh: IEEE, 2005:987-994.

[3]LIEBCHEN C. The First Optimized Railway Timetable in Practice [J]. Transportation Science, 2008, 42(4): 420-435.

[4]KROON L, MAROTI G, HELMRICH M R, et al. Stochastic Improvement of Cyclic Railway Timetables [J]. Transportation Research Part B Methodological, 2008, 42(6):553-570.

[5]廖勇.公交化城际列车开行间隔优化[J].铁道学报,2010,32(1):8-12.

(LIAO Yong. The Headway Optimization of Intercity Trains of Mass Transit Type [J]. Journal of the China Railway Society, 2010, 32(1):8-12. in Chinese)

[6]KROON L, HUISMAN D, ABBINK E, et al. The New Dutch Timetable: the OR Revolution [J]. Interfaces, 2009, 39(1):6-17.

[7]CANCA D, ZARZO A, ALGABA E, et al. Confrontation of Different Objectives in the Determination of Train Scheduling [J]. Procedia-Social and Behavioral Sciences, 2011, 20(6):302-312.

[8]CURY J, GOMIDE F, MENDES M. A Methodology for Generation of Optimal Schedules for an Underground Railway System [J]. IEEE Transactions on Automatic Control, 1979, 25(2):217-222.

[9]ALBRECHT T. Automated Timetable Design for Demand-Oriented Service on Suburban Railways [J]. Public Transport, 2009, 1(1):5-20.

[10]NIU H, ZHOU X. Optimizing Urban Rail Timetable under Time-Dependent Demand and Oversaturated Conditions [J]. Transportation Research Part C Emerging Technologies, 2013, 36(11):212-230.

[11]BARRENA E, CANCA D, COELHO L C, et al. Exact Formulations and Algorithm for the Train Timetabling Problem with Dynamic Demand[J]. Computers & Operations Research, 2014, 44(3):66-74.

[12]HASSANNAYEBI E, SAJEDINEJAD A, MARDANI S. Urban Rail Transit Planning Using a Two-Stage Simulation-Based Optimization Approach [J]. Simulation Modeling Practice & Theory, 2014, 49:151-166.

[13]TIAN Q, ZHANG J, WANG H. Equilibrium Properties of the Morning Peak-Period Commuting in a Many-to-One Mass Transit System [J].Transportation Research Part B, 2007,41(6):616-631.

[14]程婕,彭其渊,赵军. 城市轨道交通列车交路优化模型[J]. 西南交通大学学报, 2013, 48(6):1116-1121.

(CHENG Jie，PENG Qiyuan，ZHAO Jun. Train Routing Optimization Model for Urban Rail Transit [J]. Journal of Southwest Jiaotong University, 2013, 48(6):1116-1121. in Chinese)

[15]王媛媛,倪少权.城市轨道交通大小交路模式列车开行方案的优化[J].铁道学报,2013, 35(7):1-8.

(WANG Yuanyuan, NI Shaoquan. Optimization of Train Schedules of Full-Length Short-Turn Operation Modes in Urban Rail Transit[J]. Journal of the China Railway Society, 2013, 35(7):1-8. in Chinese)

[16]凌俊,胡雄,何红弟,等.城市轨道交通非高峰期列车交路方案优化[J].铁道科学与工程学报, 2015(1):190-195.

(LING Jun, HU Xiong, HE Hongdi, et al. Optimization of the Train Routing Scheme during the Off-Peak Period in Urban Rail Transit[J]. Journal of Railway Science and Engineering, 2015(1):190-195. in Chinese)

[17]CANCA D, BARRENA E, ALGABA E, et al. Design and Analysis of Demand-Adapted Railway Timetables [J]. Journal of Advanced Transportation, 2014, 48(2):119-137.

[18]江志彬,徐瑞华,吴强,等. 计算机编制城市轨道交通共线交路列车运行图[J].同济大学学报:自然科学版, 2010, 38(5):692-696.

(JIANG Zhibin, XU Ruihua, WU Qiang, et al. Shared-Path Routing Timetable Computer Designing in Rail Transit System[J]. Journal of Tongji University: Natural Science, 2010, 38(5): 692-696. in Chinese)

[19]王彦栋. 大小交路套跑条件下网络化城市轨道交通行车优化模型研究[J].物流技术,2011, 30(21):71-74.

(WANG Yandong. Study on Optimization Model of Urban Transit Network Organization and Coordination with Long and Short Routing [J]. Logistics Technology, 2011, 30(21):71-74. in Chinese)

[20]FU L, DESSOUKY M. Models and Algorithms for Dynamic Headway Control [J]. Computers & Industrial Engineering, 2017, 103:271-281.

[21]LIN C H, LIN P L. Improving the Non-Dominated Sorting Genetic Algorithm Using a Gene-Therapy Method for Multi-Objective Optimization [J]. Journal of Computational Science, 2014, 5(2):170-183.

[22]席裕庚,柴天佑,挥为民.遗传算法综述[J].控制理论与应用,1996, 13(6):697-708.

(Xl Yugeng, CHAI Tianyou, YUN Weimin. Survey on Genetic Algorithm [J]. Control Theory and Applications, 1996, 13(6):697-708. in Chinese)