基于优先权排队的顾客均衡行为

岳艳萍

（山西大学经济与管理学院，太原030006）

一、模型描述

本文就是否具有强占优先权的两类客户进行讨论。为了研究的方便，针对所研究的模型进行了一些假设。

（一）模型假设

（1）假设系统中存在两类潜在客户，即客户1和客户2，客户1是指具有优先权的客户，而客户2是指不具有优先权的客户。

（2）两类客户的平均到达率为λ1和λ2，总的到达率为λ1+λ2=λ。

（3）该排队模型为M/M/1模型。每个客户的服务时间是随机的，且都服从负指数分布。记每个客户的服务时间为S，平均服务时间为μ-1。

（4）记有优先权客户在系统中的平均排队等待时间为Wq1，平均逗留时间为Ws1；没有优先权的客户在系统中的平均排队等待时间为Wq2，平均逗留时间为Ws2。

（5）每类客户在服务完成后所获得的价值为vi，等待成本为di且d1＞d2；客户为拥有优先权所支付的价格为P，且P＜W1。

（二）模型分析

据上述假设可以求得有优先权的顾客在系统中的逗留时间Ws1以及没有优先权的顾客在系统中的逗留时间Ws2。此外，还可以推断出顾客选择进入系统的条件。

1.顾客的逗留时间

（1）当有优先权的顾客到达系统时，他所需的等待时间由两部分构成，一部分是正在排队等待服务的有优先权顾客的服务时间，另一部分是等待正在服务的服务窗空出来的时间（有优先权的顾客）。

(1)项目引导。本专业的人才培养通过三个递进式阶段项目进行贯穿。这三个阶段项目能更好地保证学生获得所需的专业基本能力、专业核心能力和专业综合能力。将项目贯穿到课堂教学中，以项目实施的过程为主线，把知识点分散到项目的各个任务中进行传授，培养学生的岗位技能并具有可持续职业发展潜力。

（2）当没有优先权的顾客到达系统时，若记Ws1～2表示有优先权和没有优先权顾客在系统中时每一名顾客的平均逗留时间，则：

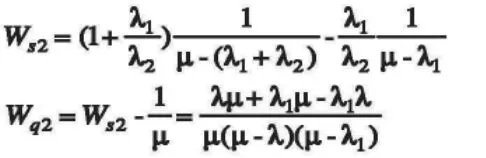
2.顾客进入系统的条件

根据上述假设，我们可以得到两类客户的预期效用值分别为：

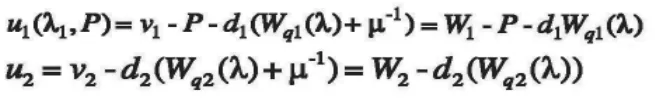
当ui≥0时，顾客选择进入系统，且当ui=0，顾客以任意概率进入系统。令ui（λi，p）时，所求得的λi（P）为第i类客户选择进入系统的最大到达率。因为第一类客户为有优先权的的客户，所以第二类客户是否选择进入系统受到第一类客户的影响。

对λ1（P）求一阶导数以及二阶导数可得λ′1（P）＜0，λ″1（P）＜0。故λ1（P）是严格递减的，且关于P是凹函数。

二、均衡客户行为

在这一部分中，主要探讨的问题是两类客户在不同的到达率以及效用情况下的进入概率。首先我们可以依据两类客户效用值的大小分为两种情况：u1＞u2和u1＜u2。本文中我们只考虑u1＞u2的情况。由于第一类客户是具有优先权的客户，因此，第二类客户是否选择进入与第一类客户的选择有很大的关系。

令 u1=u2，则：

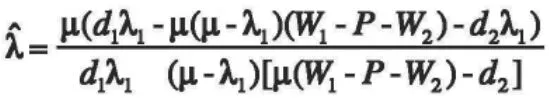
构造函数F（λ）=u1-u2，对F（λ）求导，可得F′（λ）＞0，由于λ＜λˆ且 F（λˆ）=0；又因为 F（λ）为增函数，因此可得 F（λ）＜0，也即u1＜u2。根据u1，u2之间的相对大小，可以判定两类客户选择进入系统的意愿的强弱。若u1＜u2，那么不具有优先权的顾客选择进入系统的意愿更强；反之，具有优先权的顾客选择进入的意愿更强。

因为u1（λ1，P）关于λ1递减且u1=0时，λ1=λ1（P）。根据u1和0之间的相对大小，我们可以判定λ1和λ1（P）之间的相对大小。当0＜λ1＜λ1（P）时，具有优先权的客户选择进入系统；反之，则不进入系统。

定理 当 λ＞λˆ，也即u1＞u2时，可以将两类客户的效用值大小分为三种情况：

（a）当 u1＜0，u2＜0 时，两类客户都不进入系统。

（b）当 u1＞0，u2＞0 时，第二类客户选择不进入系统，且当λ1≥λ1（P）时，客户的均衡进入率为（θEQ1（P），θEQ2（P））=（λ1（P）/λ1，0）；

当λ1＜λ1（P），客户的均衡进入率为（θEQ1（P），θEQ2（P））=（1，0）。

（c）当 u1＞0，u2≥0 时，第一类和第二类客户都可以选择进入，但第二类客户进入概率取决于第一类客户的进入率。

I.当λ1＜λmax＜λ1（P）或λ1＜λ1（P）＜λmax时，客户的均衡进入率为（θEQ1（P），θEQ2（P））=（1，（λmax-λ1）/λ2）。

II.当λmax＜λ1＜λ1（P）时，客户的均衡进入率为（θEQ1（P），θEQ2（P））=（λmax/λ1，0）。

当某类客户在完成服务后所得的效益值小于零时，该类客户没有进入系统的意愿。故（a）情况下两类客户都选择不进入系统。因为u1＞u2，故相较于第二类客户来说，第一类客户进入系统的意愿更强，所以应该首先考虑让第一类客户进入。在（b）情况下，因为第二类客户没有进入系统的意愿，故只需要考虑第一类客户的情况。当第一类客户的进入率大于系统可容纳的该类客户的最大进入率时，第一类客户部分进入；反之，则全部进入。在（c）情况下，第一类和第二类客户都有选择进入的意愿。当第一类客户的到达率没达到系统可容纳的该类客户的最大进入率时，或已到达系统可容纳的该类客户最大进入率，但未达到总的最大进入率时，也即系统仍有能力服务第二类客户时，再考虑让第二类客户进入。（c）I情况下，由于第一类客户的到达率既未达到系统可容纳的该类客户的最大进入率，又未达到总的最大进入率，所以第一类客户全部进入，第二类客户部分进入。（c）II情况下，第一类客户的到达率小于第一类客户进入的临界值而大于总的最大进入率，所以第一类客户部分进入而第二类客户不进入。

三、结论与扩展

从这项研究中所获取的信息是：潜在的市场结构对顾客的决定都起着关键的作用。因此，顾客在做出决定之前必须要充分研究潜在的市场结构。这是由于不同类别的消费者对于价格、等待时间、服务预期收益等的不同而导致的。

参考文献：

[1]Wenhui Zhou，Xiuli Chao，Xiting Gong．Optimal Uniform Pricing Strategy of a Service Firm WhenFacing Two Classes of Customers[J]．Productionand Operations Management，2014，（4）：676-688．

[2]陆传赉．排队论（第2版）[M]．北京：北京邮电大学出版社，2009．