深空探测天文测角测速组合自主导航方法*

张 伟

(1.上海卫星工程研究所·上海·200240;2.上海市深空探测技术重点实验室·上海·200240)

0 引 言

深空探测具有飞行距离远、飞行环境未知因素多、飞行程序复杂、器地通信时延与损耗大、存在跟踪盲区与天体遮挡、自主性要求高等特点,对导航能力提出了更高的要求[1]。为了确保未来深空探测重大工程任务的顺利实施,提高深空任务的成功率,降低工程技术风险,深空自主导航是必须且亟待突破的关键技术之一[2-3]。

当前深空自主导航技术大多通过天文测角或测距信息来实现导航状态的实时估计[4-5],受目标天体观测条件的约束,无法保证长期获取实时的、连续的导航信息[6-7]。然而,天文光学信息中蕴含的光谱特征及其频移量包含了探测器的速度信息,若能够充分利用空间天然资源,如直接获取光谱测速信息,可实现瞬时速度的高精度估计,进一步提高深空探测自主导航精度[8-9]。

利用天文恒星光谱测速方法瞬时速度精度高、位置精度随时间发散的特点,将其与测角导航方法相结合形成组合导航系统,可实现深空探测连续自主、实时高精度的导航。本文在组合导航系统建模的基础上,对系统的可观测性进行分析,并搭建了组合导航半物理仿真试验系统,结合火星探测工程任务背景开展仿真验证。

1 组合导航系统建模与算法

深空探测天文测角测速组合自主导航系统由三部分组成:

1)测角导航子系统:包括轨道动力学模型、测角导航敏感器和测角子滤波器;

2)测速导航子系统:包括轨道动力学模型、测速导航敏感器和测速子滤波器;

3)组合导航子系统:实现对2个子系统输出估计值的信息融合。

由于测角导航子系统的速度信息是通过位置差分获得的,其瞬时速度估计精度不高;测速导航子系统的位置信息通过速度积分获得,存在随时间发散的问题。通过对测角、测速信息的有效融合,可以避免测角、测速子系统的不足,实现对定位、定速信息的整体优化估计。

1.1 状态模型

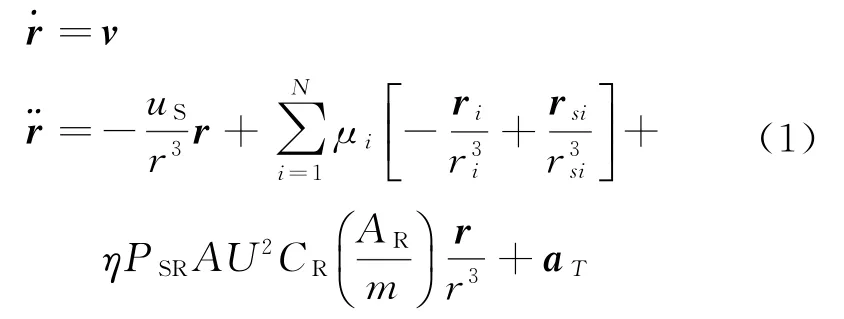
深空探测器自主导航系统的状态模型一般依据轨道动力学建立。在火星探测巡航段,主要考虑太阳、地球、火星等天体摄动,太阳光压摄动,探测器推力等因素[10]。设探测器在J2000日心黄道惯性坐标系下的位置矢量为r=[x,y,z]T,速度矢量为v=[v x,v y,v z]T,状态变量X(t)=[x,y,z,v x,v y,v z]T,则轨道动力学方程可以表示为:其中,第一项表示以太阳为引力中心的引力加速度项,uS为太阳引力常数;第二项表示考虑的行星第三体引力摄动加速度项,ri是第i个行星在日心黄道惯性系下的位置矢量,μi是对应的行星引力常数,N=1,2,3,…表示行星的编号,r si为行星相对探测器的位置矢量;第三项是太阳光压摄动加速度项,η是阴影因子,PSR是距离太阳1AU处的光压,CR为探测器的表面反射系数,AR是垂直于太阳光线方向的探测器横截面积,m是航天器的质量;最后一项表示探测器推力加速度项。

综上,探测器轨道动力学方程为

其中,W(t)是模型噪声,一般作高斯白噪声处理。

1.2 量测模型

1.2.1 测角量测方程

如图1所示,在巡航段末期,探测器将逐步靠近火星,火星的视星等逐步减小。探测器利用星上导航敏感器和太阳敏感器获得火星、太阳的光学图像,进而提取参考天体相对于探测器的视线方向矢量,然后结合导航滤波算法实现自主导航[11]。

图1 测角导航原理示意图

在日心惯性坐标系中,由几何关系有:

其中,l ps为太阳相对探测器的视线方向矢量,l pm为火星相对探测器的视线方向矢量,可通过导航敏感器测量获得;l sm为由太阳指向火星的方向矢量,可通过星历解算获得。

探测器在惯性系中的位置为

即

其中,l ps和l pm可通过导航敏感器及太阳敏感器获得,其观测量模型有:

其中,V ps、V pm为视线矢量观测噪声。

取r的观测值为Z,则观测方程有

对式 (7)在l ps和l pm处泰勒展开得

忽略观测量中的高阶小量,则

其中,观测误差

其中,V ps、V pm是量测噪声,一般作高斯白噪声处理。

1.2.2 测速量测方程

深空探测器在接收恒星光谱时,若深空探测器相对于恒星的位置是变化的,那么所接收的光谱和相对静止时相比就会有波长的漂移,波长的漂移表现在光谱上就是谱线的移动[12-13]。根据多普勒原理,波长的漂移量与探测器相对恒星静止时的波长之比等于视向速度与光速之比,即

其中,vr为视向速度,c为光速,Δλ为波长漂移量。

采用非对称空间外差干涉测速方法,仪器感知恒星辐射信号并获得干涉信号,其相位移动量δφ与相对视向速度的关系为[14]

其中,Δd为设计光程差,视为不变常量;σ为线心波数,是光波长λ的倒数。通过采集并反演干涉图像,可计算获得速度值。

从天文光谱测速导航仪解算得到相对运动速度的大小。假设探测器、恒星在日心黄道惯性坐标系下的运动速度为v、vStar,探测器相对恒星视线方向为lStar,那么探测器相对单颗恒星的运动速度大小为

其中,vStar、lStar是恒星在参考惯性坐标系下的速度和视线方向矢量,可由星表获得。

如图2所示,建立以探测器相对太阳及其他2颗恒星的视向速度为量测的观测方案,则

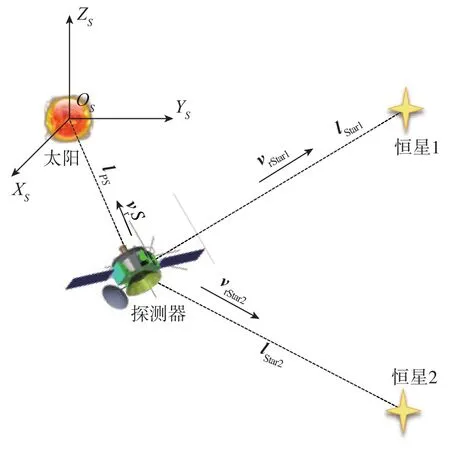
图2 测速导航原理示意图

分析式 (14)可知,为了能够完全反演得到探测器在惯性参考坐标系下的速度矢量,v的系数矩阵[lStar1lStar2lStar3]必须可逆,即探测器相对3颗恒星的视线方向必须非共面。

以探测器相对太阳及2颗恒星的视向速度大小为量测量,则量测方程为

其中,V是量测噪声,一般作高斯白噪声处理。

1.3 组合自主导航算法

与EKF相比,对于非线性很强的系统,UKF算法不需要计算雅可比矩阵,即不需对状态方程和量测方程线性化,因此模型高阶项的截断误差较小,可以获得更高的精度[15-16]。深空探测测角测速组合自主导航系统是典型的非线性系统,适合采用UKF算法。

2 组合导航可观测性分析

导航系统的可观测性反映了系统通过有限时间内的观测量确定系统状态的能力[17]。可观测矩阵是系统可观测分析的重要依据,针对强非线性系统,可以利用李导数求解系统的可观测矩阵。

忽略误差影响,导航系统方程可表示为:其中,状态矢量X∈X n⊂R n;状态方程f和观测方程h为C n内光滑的解析函数。

由微分几何理论,h沿f的各阶李导数为[18]:

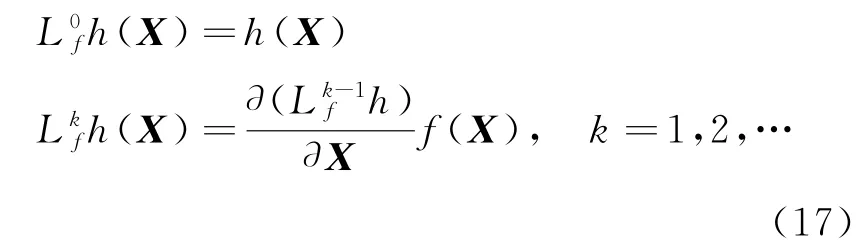
其中:

综上可得非线性系统的观测空间H。在观测空间H内,是包含状态变量和观测变量的最小线性空间。对X0∈X n,如果dH n满足可观测性秩条件,则称系统∑在X0点是局部弱可观测的。

由dH n定义的非线性系统的可观测矩阵Q(X)可以表示为[19-20]

可观测矩阵的条件数可以表征导航系统的整体可观测度[21-22],即

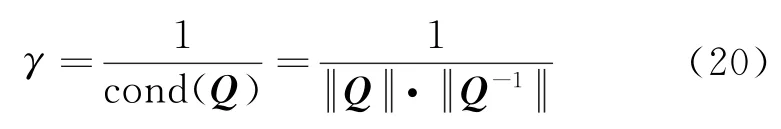
其中,σQ是Q的奇异值。分析可知,γ∈[0,1];当γ=0时,rank(Q)＜n,系统是不可观测的。该方法不依赖于观测数据,只与导航系统的模型有关,可以作为判断量测方案优劣的指标。

为了更好地对比分析系统的可观测性,本文定义系统可观测阶数:使系统可观测矩阵Q(k)满足可观测条件的最小观测次数。系统可观测阶数反映了系统状态与系统观测量之间的积分关系,可表征导航估计收敛速度和抗干扰能力。

针对测角导航及测角测速组合导航,分析导航系统的可观测性能,结果如表1所示。可以看出,视线矢量量测方案是2阶可观测,其可观测度比组合量测方案低1个数量级。

表1 可观测性分析结果

3 组合导航半物理仿真

3.1 仿真系统设计

根据测角测速组合导航总体设计,半物理仿真系统功能包括:1)模拟深空探测器不同飞行阶段的轨道与姿态动力学环境;2)为测角导航敏感器提供导航图像模拟信号;3)为测速导航敏感器提供导航光谱模拟信号;4)实现测角测速组合自主导航滤波估计,输出导航结果;5)对飞行全过程导航数据进行采集,实现性能评估。

实验系统由动力学宿主机、动力学目标机、火星模拟器、恒星光谱模拟器、测角导航敏感器、测速导航敏感器、测角导航计算机、测速导航计算机、组合导航计算机、数据存储与显示终端、性能评估计算机等组成,各部分连接框图如图3所示。

图4、图5所示为组合导航半物理仿真系统测试现场图及部分单机实物图。

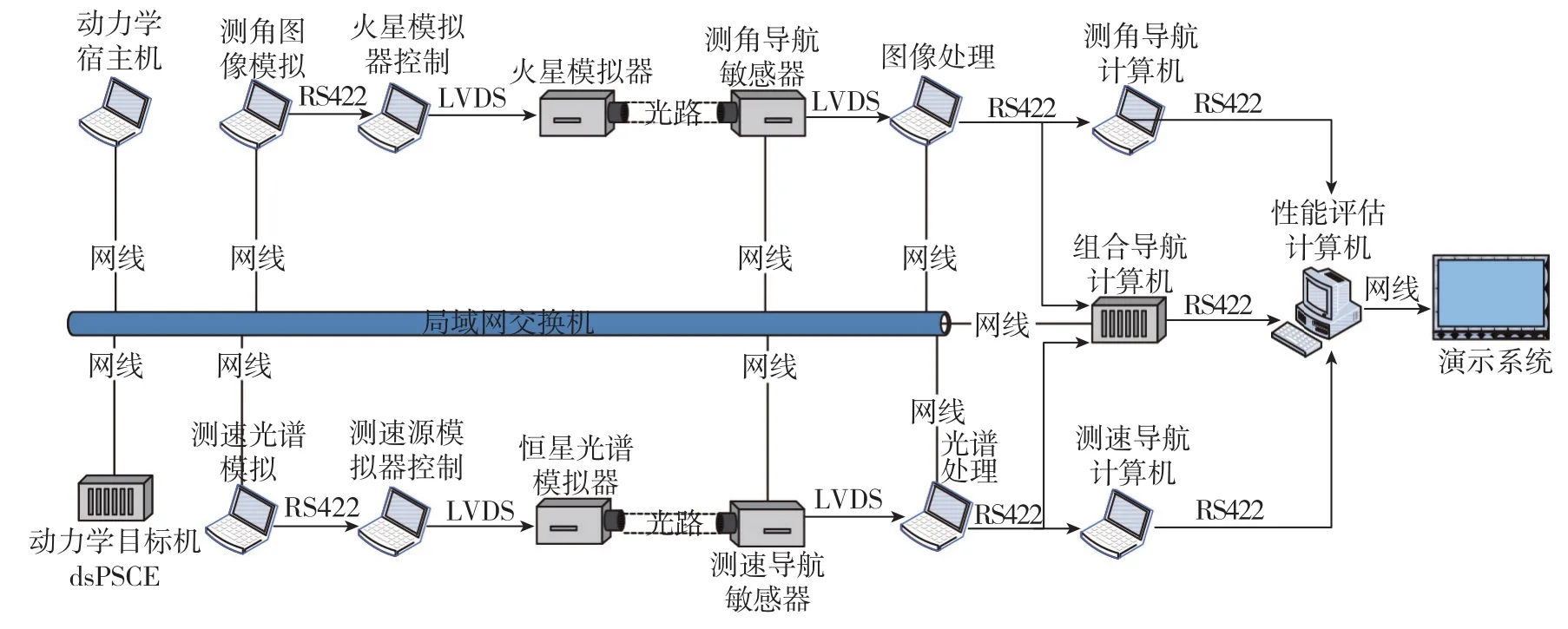
图3 组合导航半物理仿真系统连接图

图4 组合导航半物理仿真系统现场

图5 组合导航半物理仿真系统部分硬件实物图

3.2 仿真条件

探测器初始状态为:r=[60480784 216398917 6349369]km;v=[-20.2006 10.0324-0.4970]km/s。探测器初始位置偏差1000km,速度偏差100m/s。半物理仿真开始时间:2021-01-15 05:46:07 UTC,结束时间:2021-01-25 18:40:00 UTC。行星星历采用DE421;恒星数据由依巴谷星表提供,其中2颗恒星编号为45348和172167。

3.3 仿真结果分析

测角导航结果如图6所示,探测器的位置估计精度为455.7512km(3σ),速度估计精度为1.0592m/s(3σ)。在保证测角精度为2arc sec情况下,位置估计精度较高,速度估计精度较好。

图6 测角导航位置和速度估计结果

图7所示为加入3颗恒星的测速量测后的导航仿真结果,其中位置估计精度为291.1255km(3σ),速度估计精度为0.2156m/s(3σ),较测角导航精度有了明显的提升。

图7 测角测速组合导航位置和速度估计结果

对比分析上述2组仿真结果可知,由于天文光谱测速量测信息的加入,组合导航位置和速度的估计结果精度更高,收敛速度更快,有效地减弱了量测误差及星历误差等因素的影响。

4 结 论

本文针对现有深空探测自主导航方法的不足,基于天文恒星光谱测速方法的特点,将其与测角导航相结合形成组合导航系统,并给出了组合导航系统的模型及导航滤波算法。导航系统可观测度分析结果表明,组合导航系统较现有测角导航方法更优,导航估计收敛速度和抗干扰能力更强。基于火星探测工程任务,搭建组合导航半物理仿真试验系统。仿真结果表明,加入天文光谱测量信息后,有效抑制了量测误差的影响,进一步提高了导航估计精度,增强了导航系统可靠性,为实现深空探测高精度自主导航提供了新的技术途径。