交通事件下排队车辆数和总延误计算模型研究
董国华 左友兰


摘要:为描述交通事件后导致拥挤交通流中的排队现象,分析预测交通流的时空影响。根据流量守恒定律和交通波波速公式,提出了排队车辆数和车辆总延误定量计算的一个新模型。将事件后交通流的发展划分为三个时间阶段,推导出道路堵塞时各相应时间段交通变量动态计算公式。同时分析了交通事件影响因素除了事件本身的严重性外,事件的清理时间是决定事件瓶颈处车辆排队第二位的影响因素;以及交通事件时空发展模型与事件自动检测两者之间相互影响、互为因果的关系。最后用应用算例对该模型的有效性进行验证,结果表明,数据符合实际情况,排队车辆数随着事件持续时间增加呈分段线性变化,而所有排队车辆的总延误随着交通事件处理时间的增加呈二次平方变化。此模型可作为交通管理控制部门对交通事件发生后制定合理救援措施的理论依据。
关键词:交通事件;影响因素;交通流;排队车辆数;总延误;模型分析
中图分类号:TP399
文献标识码:A
1 引言
近年来,由于我国机动车越来越多,人、车、路等矛盾也越来越突出。在高速道路上,交通事故、车辆故障、货物散落、大货车占道、修路养路、路边停车、流量激增等交通事件是造成偶发性交通拥堵的主要原因,尤其是在节假日,事件发生后导致车辆排队现象在交通运输系统中随处可见。交通事件发生后,原交通流的车流量会发生改变,车流量的波动甚至会传播到其它相邻的道路上去。因此,交通事件对交通流的定量影响一直是一个倍受各方关注的问题。特别是事件发生后,排队车辆数和总延误随时间如何增长,与事件特性如交通流量、车道数、事件处理效率等有何关系,对交通流预测、事件预警以及交通管理和控制都有重大意义[1]。
国内外很多研究者一直致力于排队现象的分析和交通流参数预测。上世纪70年代,日本Akaike提出的Akaike信息准则(Akaike Information Crite-na,AIO经过各国大量实践证明,对交通流的预测精度在70%-800/0。阿里巴巴的Wanli Min[2]采用半鞅理论、网络交通模型、基于高德地图实时数据和历史数据对交通流预测准确率稳定在91010以上。Guo Huan[3]等人研究成果为基于灰色模型的短时交通流预测方法,充分考量了交通流的非线性以及延迟特征。Hani S.Mahmassani[4]等人研究探讨了在大规模复杂城市严重堵塞街道网中交通流极限关系性能,包括“死锁”的形成、传播、恢复、大小等。此拥堵现象的特点暂时很少人关注,是比较新颖的一个问题。Treiber M.、Kesting A[5]提出了一个新的跟车理论动力学模型,微观与宏观变量相结合,该模型可以很好地模拟交通流拥堵、拥堵疏散、走走停停现象和幽灵幻象等状况。王殿海[6]等人针对双向两车道路内停车路段,分流量较大和较小两种情况建立了相应的延误影响模型,并利用VISSIM仿真软件模拟数据对模型进行了验证。张晶晶[7]用交通波理论研究交通事故直接影响范围,用节点联系强度建立事故上游车辆绕行计算模型来研究间接影响范围。曹志远[8]等人基于交通事故下采取限、分流措施分析了交通波的影响,得到了交通流演变过程中的扩展时区、稳定时区、启动时区,三个时区的时空影响范围。胡继启等[9]利用海量收费数据有效计算出相邻两个收费站之间路段上的拥堵初发点位置和初发时刻,此文研究属于事件检测范畴,与本文交通事件时空发展模型相互影响、互为因果的关系。
综上所述,道路发生交通事件导致拥堵后,很多学者只是定性分析交通变量,而事件具体的发展过程如何,与事件特性、事件处理效率等因素有何关系,相关受影响的变量随时间变化的定量规律等很少有研究者关注,目前极其缺少此类问题的解决方案。因此,本文以道路公路基本路段(一條道路)和收费站匝道与一条主干道(两条道路)发生交通事件为例,分析事件具体的发展过程与影响,以及交通事件发生后不同时间段内事件点各交通变量动态计算模型,分析事件发生与事件检测两者之间有何关系,用于以后进一步的突发事件下交通流预测工作。
2 交通事件影响的三个时间阶段分析
由于交通事件的发生时间和发生地点是随机的、不可预测的,因此很难采取控制交通需求或提高道路通行能力等对策来处理,解决问题的重点在于及时发现事件,准确评估事件性质,迅速实施应对措施,并立即向其他司机通告事件情况,从而对事件实现快速、高效、恰当的处理[10]。
交通事件发生后,对于较小的事件,如只是轻微的刮擦,在不对交通运行造成影响的前提下可不进行处理,节约人力物力,以免在处理的过程中由于救援车辆的占道使事件影响更严重或增加车辆排队和延误。而对于较严重的交通事件可进行快速理赔的原则,确定责任后双方快速撤离现场,节约事件的清理时间,减小排队车辆数和车辆延误。而对于严重的交通事件可进行报案由交通管理部门处理,不过它可能需要耗费很长的处置时间,自报案到交警抵达事件现场,再到完成问题处理、恢复道路交通,不仅耽误双方时间,还会加大事件的影响力,增加车辆排队和延误。所以发生交通事件后,需要实施适当的救援措施,倘若方法不正确,很可能造成二次事件,加重交通拥堵状况。而倘若方法过当,那么极有可能产生交通资源浪费。通过以上分析可知,除了事件本身的严重性外,事件的清理时间也影响着车辆排队。
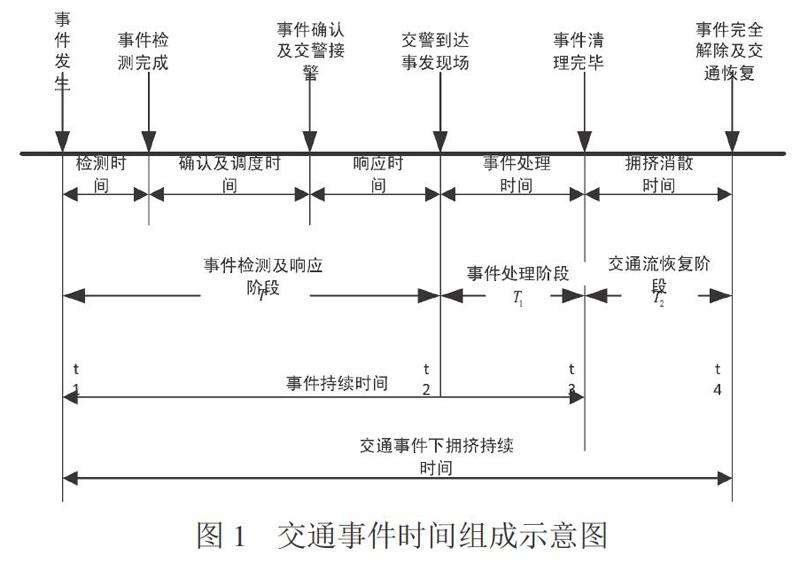
交通事件后,因为自发生交通事件开始,历经事件检测、核实情况、交警处置、清理结束、恢复交通、消除排队等环节,都要耗费相应时间。因而可将整个事件分为3个时间阶段:第一阶段时间指从事件产生至交警抵达现场进行时间处理这个期间,事件确认接警时间以T表示。第二阶段时间指从开始处理事件至交通开始恢复这一期间,对应的事件处理时间以T1表示。第三阶段时间指自现场交通恢复开始,直至事件上游车辆排队不继续增加,再到最后完全消散[11],对应的排队消散时间以T2表示。交通事件时间组成示意图如图1所示。
在T时间内,事件现场维持不变,尚未开始处理,此时可分成两中类型进行分析:(1)交通事件占据部分车道,事件位置的剩余通行能力Qs≠0,若交通事件愈重,那么Qs愈小。当上游的交通需求Q
T1时段里,当完成交通事件确认后,管理部门抵达现场开始处理,这期间事件点交通仍受持续影响,事件断面通行能力同步发生改变[13]通常会减小,甚至完全封闭。当拥挤严重时,则车辆排队加剧。在T和T1两个阶段,事件位置上游可能出现排队;如果无车辆排队,那么T2=0;如果存在车辆排队,那么要等到事件处置完成和道路交通恢复后,车辆排队状态才能逐步消除,那么T2≠0。T2可理解为交通事件的持续影响时间,具体指事故处理完成、道路恢复通行到车辆排队不继续增加这个期间,也能看成是消散波自队列首部传递到尾部所耗费的时间[14]。
由以上分析可知,交通事件发生的严重性、事件后所占用的车道数、上游交通需求以及事件清理时间等都是影响事件瓶颈处车辆排队的重要因素。而事件严不严重是事件发生时由事件本身决定的,事件后人为无法改变;而事件后所占用的车道数是由道路的物理结构和事件本身决定;而上游交通需求是由道路所在的位置和时间决定,若是处于交通运行的关键路段或节假日交通需求量大的时间段,则上游交通需求量增大,反之,上游交通需求量减小;而事件清理时间是人为决定的,是后续可控的事件影响因素。事件处理效率越高或清理时间越短,排队车辆数越少,则排队消散快些;事件处理效率越低或清理时间越久,导致排队车辆数越多,排队消散的时间也越慢。因此,交通事件众多影响因素中除了事件本身的严重性外,可控因素中只有事件的清理时间是最重要的。即事件的清理时间是事件瓶颈处决定车辆排队第二位的影响因素。
3 分时间段建立模型
根据上一部分分析可知,交通事件发生后事件演化的三个时间段中前两部分时间构成车辆排队形成阶段,到事件处理完毕恢复道路交通时,排队车辆数达到最大值,排队开始消散,即第三部分时间构成排队消散阶段。本文假设在事件处理过程中有车辆排队,即第二节中的第(1)种Q>Qs情况,则交通流可按事件点的剩余断面通行能力通过事件点,超过该通行能力的车流在事件点上游排队。由常规可知,排队车辆数和排队长度随时间线性增长,越晚加入排队,越晚离开,总延误等于所有排队车辆延误之和。
3.1 排队车辆数计算模型
通过以上分析,假设如图2所示发生交通事件的基本路段为单向三车道,设道路正常情况下通行能力为Q',在同级服务水平上,在α点发生交通事件后占用最右侧车道,而且事件处理过程中也只占用最右侧车道(即事件处理过程中事件点交通没有受到进一步影响),则道路通行能力会下降,变为剩余通行能力Qs。根据第二节分析,可设t=0时发生交通事件,即车辆开始排队,则每分钟内就有Q'-Qs辆车加入排队,t=T1时刻障碍清理完毕,下游开始疏散,疏散速度Q'> Qs,完全疏散时刻就是t=T2,根据车辆守恒定律,则有:
由于事件发生后从事件检测到事件接警处理过程中以及到事件处理完毕,这部分过程都假设交通流没有受进一步影响。而根据现实情况,在事件处理过程中,交通管理指挥者也会尽可能使交通流的影响降到最低。所以根据时间分段,可将事件检测响应阶段T与事件处理阶段T1合并。交通事件清理完毕后,道路交通恢复正常。事件下游开始消散,但由于消散波传到队尾时还需一定的时间,所以事件上游在完全消散前还在慢慢排队。则排队车辆数随时间的变化有:
3.3 延误时间动态计算模型
从3.1节可知,延误是理想行程时间和实际行程时间之差。由于没有实际的交通事件时空发展數据,本文由交通事件发展的三个时间段直接计算车辆延误,从事件发生到事件处理完毕,就是车辆的等待时间。但由于每辆车到达和离开的时间都是变化的,这里引入排队消散动态时间函数τ(t),根据每辆车到达和离开的时间不同,分别计算每辆车相应的延误,即每辆车排队等候的时间加上排队消散的时间就是每辆车所耽误的时间。通过计算出每辆车的延误,再把断面所有车辆延误之和即为总延误。
从计算公式中可知,排队车辆数随着排队形成时间和排队消散时间都是一个线性变化的关系。随着事件的发展,排队的车辆越来越多,排队车辆数随着交通事件持续时间增加呈分段线性变化。而排队车辆的总延误随着交通事件处理时间的增加呈二次平方变化。
3.4 交通参数计算步骤及算法实现
1)交通参数计算步骤
交通事件下对交通流的预测研究就是对交通流参数的预测研究。而本文中建立的模型,其实就是对交通流参数的计算预测。而基于湖南省道路交通的实际情况,湖南省交通厅的数据中心还在建设之中,目前还无法获取数据进行精确的实验,只能根据本文的实际情况,用简化假设的方法,拟确定如下方案得以实现。
首先简化交通事件实例,根据具体实例,如图2所示假设己知量,此模型中假设正常情况下,并在道路的同级服务水平条件下,假设在事件处理过程中交通流没有受到进一步的影响,则己知的量有:道路正常通行能力Q'、剩余通行能力Qs、事件清理完毕时刻T1、以及下游疏散速度Q'>Qs具体处理程序如下:
1)模型参数输入:Q'、Qs、T1;
2)根据流量守恒定律,得出T1和T2的关系;
3)根据时间分段,建立排队车辆数随时间变化的分段函数n(t);
4)以事件发生的起始位置为位置坐标原点,左边为负轴(事发地点上游),右边为正轴(事发地点下游),建立位置坐标轴x;以事件发生的起始时刻为时间坐标原点,右边为正轴建立时间坐标t;
5)根据流量密度的定义,分时间段建立下游前沿位置函数关系xdoun(t);
6)根据格林伯速度一密度模型结合交通波波速公式,得出排队车流速度Qs/ρmax
7)引入时间函数τ(t),记为消散波传输的时间。结合步骤五,再根据集结波与消散波传播的位置相等,得出消散波传输时间τ(t)函数;
8)求所有车辆的总延误D,即是对每一辆车的延误之和,利用积分法求出D;
9)模型参数输出:T2、n(t)、D。
根据以上步骤即是本文算法的实现。
2)算法实现
本文提出的交通事件后交通流参数计算算法
伪代码如下所示:
算法1.基于交通事件下排队参数计算算法
输入:Q'、Qs、T1
横坐标轴位置:x;纵坐标轴时间:t
最大密度:ρmax
阻塞密度: ρf
输出:T2、n(t)、D
4 模型分析
通过概括国内外学者的研究,交通流参数估计的模型有很多,如葛兴、王殿海等人的路内停车模型;经典红绿灯模型;姚荣涵、王殿海的拥挤交通流当量排队长度变化率模型等等。接下来主要分析经典红绿灯模型与本文提出的交通事件时空发展模型。
4.1 交通事件时空发展模型
道路发生交通事件后,人们通常关心事件发生的时间、地点,而很少有人关注事件的演化过程。事件发生持续多长时间,5 min、10 min后事件发生情况、严不严重。事件导致拥堵产生排队后,是否还能通行,车辆排队是否占据整条道,还是己蔓延到相邻路段上,如蔓延邻路段上,是否导致相邻路段也拥堵产生排队,进而波及相邻的一条道或几条道,导致整个路网产生拥堵,甚至“死锁”现象的发生。
根据谢立新[14]在2016年湖南省高速公路工作会议工作报告中的数据显示,到2015年底全省高速公路通车里程达到5653公里,这么多公里数分成多条高速公路并且有的相互互通,毋庸置疑收费站也不少。而高速道路收费站拥堵导致排队现象常有发生,节假日拥堵严重的时候在收费站排队花费5、6个小时是人们通常遇到的问题,那么如何快速准确地对拥堵情况、事件演变信息进行定位,及时发布相应的道路运行状态信息,是交通管理者和出行者最关心的问题。如图5所示为一个高速公路出口匝道。当人们在收费站口等候出行时,由于车辆过多产生排队,甚至一直排到匝道上去了,如果人工收费使车辆放行速度比车辆到达速度慢,排队将一直增加,可能蔓延到主干道,继而导致主干道也拥堵排队,继而发生交通事件。因而从一条道路发生交通事件,对事件进行检测以及对交通流参数进行评估分析,到波及相邻路段发生交通事件、对事件影响的交通变量又进一步进行分析预测。而事件检测的数据结果可以作为交通流参数估计的数据输入,进而对交通流进行预测;而对交通流预测的数据结果反过来又可以作为交通状态判别的数据输入。其实这就是从事件发生到事件检测再到对事件影响下交通流参数进行评估预测的一个闭环,这两者的研究结果相互影响、可相互作为各自模型的参数输入,即交通状态判别与交通量计算两个模块是相互耦合、串联的关系。
4.2 经典红绿灯模型
红绿灯模型中假设道路交通在开始时处于稳定状态,车流密度是常数,某个时刻路口的交通灯红灯突然亮了,于是交通灯前面的车辆继续行驶,而后面的车辆一辆一辆开始排队拥堵起来。经过一段时间后,绿灯亮了,排队的车辆开始消散。姜启源[15]等人用交通流的模型描述了这个过程,并且绿灯亮后对堵塞车辆多长时间能追上远离的车队进行了计算,以及多长时间排队能消散,使道路交通恢复正常。
由以上分析可知,(1)红绿灯模型与本文模型相似,也可看作一次交通事件的发生和解除的模拟。红灯开始时刻即为事件发生时刻,绿灯亮的时刻就是事件清理完毕、排队开始消散时刻;而整个事件持续5分钟后解除,即持续5分钟的交通事件要75分钟排队才能消散。(2)红绿灯模型中的红灯时间τ越短,道路交通恢复时间t1越短,这说明事件的清理时间影响着车辆的排队,与本文模型相一致,除了事件本身的严重性以外,事件的清理时间是决定排队第二位的影响因素。(3)红绿灯模型时间上具有周期性、地点也是固定的,而本文模型中交通事件发生的时间、地点都是随机的。本文模型或事件现象更复杂、更难描述,因此更有研究的价值。(4)红绿灯模型相当于道路封闭5分钟,道路完全不能通行,而本文模型在道路发生交通事件后还有剩余通行能力,不是完全封闭状态。红绿灯模型就是本文模型中的一个特例,即本文模型中剩余通行为零的极限情况,在日常生活中除了红绿灯之外是普遍存在的交通事件类型,适用性更广,更有实际应用价值。
5 应用算例
如图5所示,设某道路公路基本路段长度为500 m,单方向车道数为3,一个车道宽度为3.5 m。在道路上t=0时刻发生了一起交通事件,事件车辆占用一个车道6= 3.5 m,长度约为a=7m,事件點上游路段长度为300 m。假设道路正常情况下,单方向每分钟100辆车通过,在同级服务水平上,若事件导致流量下降40%,单方向每分钟只有60辆车通过,则单方向每分钟有40辆车加入排队,检测延误30秒的话,将影响到20辆车。
如图2所示发生交通事件的道路基本路,根据公式(1),设t=0时车辆排队开始,则有
分别设T1为5 min、30 min、60 min时刻,障碍清理完毕,根据公式(3)、公式(6)、公式(8),分别计算出排队消散时间、最大排队车辆数、总延误如表1所示。
从表1中可以看出,此文模型计算出的各个交通变量结果比较接近实际情况。从车辆的总延误时间来看,当T1=5 nun时,200辆车的车队总延误时间约为833 min,每辆车延误约为4 min。把道路上的车辆都折算成小汽车的长度,包括车辆前后间距,每一辆车折算6米长,则200辆车的最大排队长度约为1.2千米。当T1=30 min时,1200辆车的车队总延误时间约为30000 min,每辆车延误约25 min,而1200辆车的最大排队长度为7.2千米。此模型是在车流较大的情况下对数据拟合较好,要是高速道路严重堵塞、密度更大的情况下,如图4.1所示的收费站匝道,车辆排队7.2千米的话,匝道排队肯定溢出。如若收费站放行速度比车辆到达速度慢,相当于交通需求Q> Qs,又或许道路的通行能力变得更小,后来的车辆继续排队,而一般匝道都是几百米,所以排队肯定排到主干道上去了,导致主干道也拥堵排队甚至发生二次交通事件。则此情况属于拥堵在交通路网上的传播模式。
6 结束语
本文对道路交通事件影响下不同时间段内交通变量的动态变化进行了新的建模,较之经典红绿灯模型更有实际应用价值。(1)本文通过分析得出,除了事件本身的严重性外,事件的清理时间是决定事件瓶颈处车辆排队第二位的影响因素;(2)以高速公路出口匝道为例,用简化假设的方法分析了交通事件时空发展模型与事件检测两者之间的数据结果可以作为各自模型的数据输入,即两者研究的数据结果相互耦合、影响、串联的关系;(3)通过应用算例分析,在道路交通流量较小的情况下,排队车辆数随着交通事件持续时间增加呈分段线性变化,而所有排队车辆的总延误随着交通事件处理时间的增加呈二次平方变化。流量较大或者剩余通行能力变小的情况下,道路车辆排队溢出,使相邻路段也受到影响。(4)下一步计划是考虑动态瓶颈下交通事件影响模型、拥堵在公路网中的时空扩散,以及交通状态判别与交通量计算两个模块具体的耦合。
参考文献
[1]梅朵.基于云计算的交通瓶颈控制与诱导协同模型研究:[D].长春:吉林大学,2015.
[2]闵万里,劳拉.温特.实时道路交通预测与时空相关[J].交通研究C部分,2010,l9(2011):8-11.
[3]郭欢,肖新平,福雷斯特.基于延迟的城市道路短期交通流量预测模型[J].交通运输系统工程与信息技术学报,2013,l3(6):60-66.
[4]MAHMASSANI H S,SABER M,ZOCKAIE A.城市网络僵局:理论,特征和动态[J].运输研究C部分:2013,36:480-497.
[5] TREIBER M,KESTINC A.动态交通流[M].纽约,斯德哥尔摩柏林海德堡,2013.
[6]王殿海,葛兴,姜波.路内停车对交通流的延误影响模型U].城市交通,2009,7(2):1-5.
[7]张晶晶.路网环境下高速公路交通事故影响传播分析:[D].西安:长安大学,2010.
[8]曹志远,郭忠印,张起森,等.高速公路重大交通事故时空影响范围研究[J].公路工程,2011,36(6):56-58.
[9]胡继启,彭建,董国华,等.基于收费数据的交通拥堵出发点计算[J].计算机工程与应用,2015.15(1):l-7.
[10]邹力.物联网與智能交通[M].北京:电子工业出版社,2012.
[11]陈诚,谭满春.交通事故影响下事发路段交通流量变化分析[J].科学技术与工程.2011,11(28)1-2.
[12]张凡.典型交通事件下道路拥堵的网络化蔓延特性研究[D].北京:北京交通大学,2014.
[13] WACENINGEN -KESSELS F.多类交通流模型:分析与仿真方法[D].荷兰:荷兰研究学院T-RAIL:代尔夫特理工大学,2013 年.
[14]谢立新.努力实现“十三五”高速公路发展精彩开局[A].2016年全省高速公路工作会议工作报告[C].长沙:湖南省高速公路管理局,2016:1-2.
[15]姜启源.数学模型[M].北京:高等教育出版社,2011.

