级联多电平逆变器有限控制集模型预测控制
朱厚达 陈才学 刘凯 廖凯

摘要:针对传统级联多电平逆变器的有限控制集模型预测控制(FCS-MPO计算量随电平数增加而指数增长的缺点,本文提出了改进的级联多电平逆变器FCS-MPC控制算法。首先,分析级联多电平逆變器的数学模型,探讨了FCS-MPC控制策略在级联多电平上的应用原理,在传统FCS-MPC控制的基础上,对电流进行延时补偿、反馈补偿及参考电流校正,提高了系统的跟踪特性和减少了电流谐波畸变率;其次,将复杂分区内电压矢量的追踪计算简化至在单一分区内进行,优化开关冗余状态,减少计算量。最后搭建了MATLAB仿真实验,与传统FCS-MPC算法对比分析,证明了此方法的正确性和优越性。
关键词:级联多电平逆变器;有限控制集模型预测控制;简化分区计算
分类号:TP273
文献标识码:A
1 引言
与应用快速充电电容(FO、中性点箝位(NPO的多电平逆变器相比,级联多电平逆变器具有高扩展性、高可靠性、高功率因数等优点,是当前输配电系统中电力电子装置的主电路拓扑结构之—[1-4]。
目前有多种级联多电平逆变器控制方法,如PWM、PD-SPWM等[5-7],其中有限控制集模型预测控制(FCS-MPO因响应速度快、稳态误差小、算法构造灵活等特点备受青睐[8-11]。传统FCS-MPC通过遍历各个电压矢量来预测下一周期的电流,当电压矢量数较多时,计算结果在一个采样周期内难以应用;此外,传统FCS-MPC在实际应用中存在计算延时,使系统采样点与开关状态作用时刻不匹配。文献[12]对FCS-MPC进行延时补偿,系统整体表现达到预期,然而并未对补偿后的电流进行反馈校正,电机参数出现误差,系统在低速带载的情况下转速偏高;文献[13]令下一时刻的输出电流等于当前时刻的参考电流,将电流追踪转换为对电压的追踪,实现无差拍控制,然而参考电流在坐标系中旋转进而产生误差,使输出电流脉动;文献[14]介绍了一种只考虑临近向量分区的模型预测控制算法(MPC -adj),将电压矢量分为6个区域,并在上一时刻的最优电压临近的六边形区域内选择当前时刻的最优电压相量,系统的计算量显著减少,然而降低了系统的瞬时响应。
本文提出改进的级联多电平逆变器FCS-MPC控制算法,在传统FCS-MPC算法的基础上,对电流进行延时补偿、反馈补偿及参考电流校正,根据电压矢量空间分区的对称性对电压矢量进行简化,将复杂分区内电压矢量的追踪计算简化至在单一分区内进行。该算法提高了系统的跟踪特性和扩展性,减少了计算量和电流谐波畸变率。最后通过仿真实验证明该算法的正确性和可行性。
2 级联多电平逆变器的数学模型
2.1 拓扑分析
图1为三相级联逆变器拓扑结构。其中E为直流侧电压,L为并网电感,R为滤波电感电阻和线路等效电阻之和,ix为逆变器输出的各相电流,ex为电网各相电压,其中x={a,b,c}。
由图1可知,级联逆变器电压矢量数计算公式为
N= (2n+1)3 (1)
式中,n为一相桥臂上H桥单元的个数。
以逆变器中性点为参考地,级联逆变器的相电压计算公式为:
3 传统FCS-MPC原理
传统FCS-MPC开关函数选择过程如图2所示,其中N为多电平级联逆变器电压矢量数。由于级联逆变器的模块化结构,其开关器件数增减灵活,采用传统FCS-MPC所需要计算的电压空间矢量数变化大。
4 改进的FCS-MPC算法
本文提出的FCS-MPC算法是在对系统采样参数进行延时补偿、反馈补偿以及参数修正计算后,将所求得的参考电压向量所在三角区域内三个电压矢量纳入下一步计算,使得系统对下一参考电压向量所产生的系统瞬时响应保持较高的动态响应。
文献[16]中提到,当要考虑延时补偿时,采取2个采样周期进行预测,对式(8)运用延时补偿计算,可以得到预测电流iα(k+2)、iβ(k+2)。
4.1 电压矢量区间的简化与选择
为了简化电压矢量区间计算,如图3所示本文将电压矢量分为六大三角形分区,据式(13)求得最优的电压矢量后,将其转换至第一分区进行开关状态选择。分区判定公式如下:
综上所述,级联多电平并网逆变器控制框图如图4所示。
以图5作为分区依据,l区内三角区域的相邻电压相量以及参考相量所在三角区域的确定如表2所示。
5 仿真实验
为了证明本文提出方法的优越性和可行性,在Matlab14b中搭建了五电平的级联并网逆变器仿真实验,并与传统FCS-MPC分三个方面在同等条件下进行比较。主电路和其他仿真参数如表3所示。
5.1 稳态并网电流与THD
图6、图7分别为稳态时传统FCS-MPC与改进算法在级联五电平逆变器上的并网电流波形。
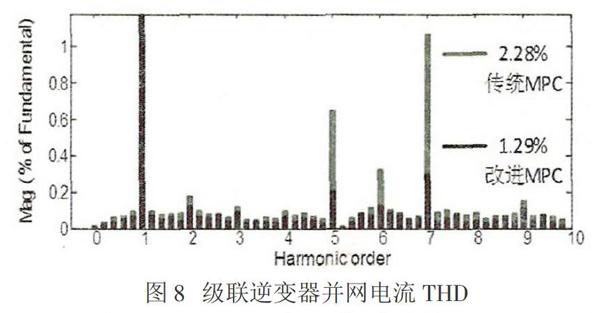
通过对比可知,稳态工作时传统FCS-MPC与本文提出的控制方法均能使系统稳定运行,然而在谐波控制方面,如图8所示,基于传统FCS-MPC算法的级联逆变器并网电流THD为2.28%,使用改进算法后的级联逆变器并网电流THD为1.29%,改进算法表现更加优异。
5.2 运算效率
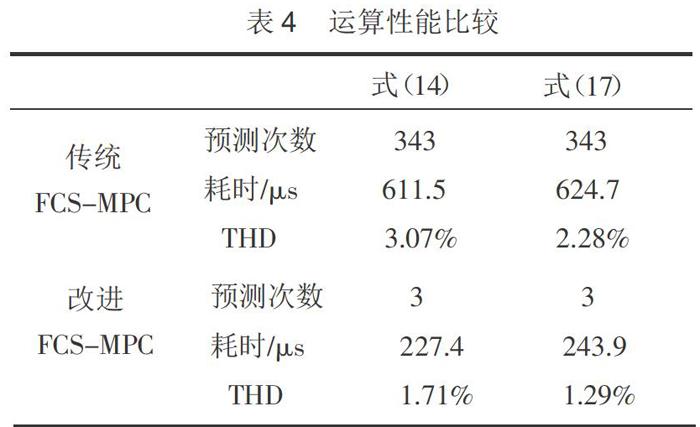
为了比较传统FCS-MPC与改进算法的运算效率,采用不同评估函数分为预测次数、耗时及THD三部分进行对比,结果如表4所示。
从表4可以看出,由于评估函数选取为给定值和预测值误差的平方项,能抑制高次谐波的产生,因此本文提出的改进算法在不同评估函数中的THD值均优于传统FCS-MPC,同时可以看出计算效率,且随着模块数的增多,效率更加明显。
5.3 电流动态性能
为了更好的验证本文提出方法具有很好的动态性能,使参考电流在O.ls处发生阶跃变化。由图9可知采用传统FCS-MPC并网电流跟踪有一定的迟缓,并且调节过程中超调量大。采用改进算法时,通过图10可以看出输出电流快速的追踪了参考电流,系统瞬态响应优異。
6 结论
在传统的FCS-MPC算法基础上提出一种基于FCS-MPC的级联多电平逆变器控制策略。与传统的FCS-MPC算法相比有如下优点:
(1)提高了系统的跟踪特性和减少了电流谐波畸变率;
(2)优化开关冗余状态,减少计算量;
(3)扩展性强,能适用于任意电平的级联逆变器。
最后通过仿真实验验证了本文方法的有效性和可行性。
参考文献:
[1] ACUILERA R P,LEZANA P,QUEVEDO D E.Switched ModelPredictive Control for Improved Transient and Steady -StatePerformance[J],in IEEE Transactions on Industrial Informatics,Aug.2015,11(4):968-977.
[2] ACUNA P,MORAN L,RIVERA M,et al.A Single-OhjectivePredictive Control Method for a Multivariable Single -PhaseThree-Level NPC Converter-Based Active Power Filter [J],inIEEE Transactions on Industrial Electronics,2015,62 (7):4598-4607.
[3]周飞,何维国,包海龙,等.适合城市电网的级联型统一潮流控制器[J].电网技术,2012,36 (03):174-178.
[4] Yu Y, KONSTANTINOU G,HREDZAK B,et al.Power Balanceof Cascaded H-Bridge Multilevel Converters for Large-ScalePhotovoltaic Integration [J].in IEEE Transactions on PowerElectronics, 2016, 31(1):292-3 03.
[5]顾春阳,郑泽东,李永东.用于机车牵引的新型级联H桥整流器电压平衡方法[J],电工技术学报,2013,28 (12):168-172.
[6] CHAVARRIA J,BIEL D,CUINJOAN F,et al.Energy- BalanceControl of PV Cascaded Multilevel Crid- Connected InvertersUnder Level- Shifted and Phase-Shifted PWMs [J],in IEEETransactions on Industrial Electronics, 2013, 60(1):98-111.
[7]刘云峰,何英杰,尹仕奇,等.基于空间矢量调制的星形级联H桥svc直流侧电压控制方法研究[J].电工技术学报,2015,30(5):23-32.
[8] KAKOSIMOS P,BAYHAN S,ABU -RUB H.Single -phasecascaded H -hridge neutral -point clamped inverter:Acomparison between MPC and PI control. IECON 2016 - 42ndAnnual Conference of the IEEE Industrial Electronics Society,Florence,2016:5983-5989.
[9] BOCKER J,FREUDENBERC B,DIECKERHOFF S.ExperimentlComparison of Model Predictive Control and Cascaded Controlof the Modular Multilevel Converter [J],in IEEE Transactionson Power Electronics, Jan. 2015,30(1).422-430.
[10] RIVERA M.A Comparative Assessment of Model PredictiveCurrent Control and Space Vector Modulation in a Direct MatrixConverter [J],in IEEE Transactions on Industrial Electronics,2013,60(2):578-588.
[11] AGHDAM M M,LI L,ZHU J,et al.Finite control set modelpredictive control -a powerful control algorithm for grid -connected power converters [C],2016 IEEE llth Conference onIndustrial Electronics and Applications (ICIEA) ,2016:2350-2355.
[12]张永昌,杨海涛.异步电机无速度传感器模型预测控制[J].中国电机工程学报,2014, 34 (15):2422-2429.
[13]曹晓冬,谭国俊,王从刚,等,三电平PWM整流器多模型预测控制方法[J].电工技术学报,2014, 29 (8):142-150.
[14] KWAK S,PARK J C.Predictive Control Method With FutureZero-Sequence Voltage to Reduce Switching Losses in Three-Phase Voltage Source Inverters [J].in IEEE Transactions onPower Electronics, 2015, 30 (3):1558-1566.
[15] VAZQUEZ S.Model Predictive Control: A Review of ItsApplications[J],in Power Electronics,in IEEE IndustrialElectronics Magazine, 2014,8(1):16-31.
[16]沈坤,章兢,王坚.一种多步预测的变流器有限控制集模型预测控制算法[J].中国电机工程学报,2012,32 (33):37-44.
[17] KWAK S,PARK J.C.Switching Strategy Based on ModelPredictive Control of VSI to Obtain High Efficiency andBalanced Loss Distrihution U], in IEEE Transactions on PowerElectronics, 2014, 29 (9).4551-4567.
[18]陆治国,王友,廖一茜.基于光伏并网逆变器的一种矢量角补偿法有限控制集模型预测控制研究[J].电网技术,2017,1-6.

