复杂网络视角下企业集群技术创新扩散仿真研究

卢燕群，何永芳

(西南财经大学工商管理学院，四川　成都　610031)

0　引言

企业集群是指在一个特定的区域内，企业通过水平或垂直层面所展开的经济技术合作和竞争所形成的空间邻近的产业群体[1]。随着国内外环境因素影响，传统企业集群发展面临着严峻的挑战。为了推动创新发展战略和适应经济发展新常态，企业集群需要加快科技创新、推动企业转型发展[2-3]。中关村国家高新技术园作为中国战略性新兴产业发源地，园区内互联网、大数据等创新型企业已率先改变传统行业，成为全国产业转型升级的引擎[4]。唐山高新区内创新型企业的研发成果直接带动了当地煤炭、钢铁等产业的转型升级；长沙凭借中联重科、三一重工、山河智能等企业的创新成果，带动当地其他企业实现转型升级[5]。企业集群中高新技术和先进适用技术通过技术创新扩散，对产业改造和提升具有重要作用，有利于经济结构高端化发展。因此，研究技术创新在企业集群中的扩散过程和规律，有针对性地提高技术创新扩散效果，具有非常重要的研究意义。

从研究视角来区分，创新扩散模型可以分为宏观扩散模型和微观创新扩散模型。宏观扩散模型主要集中于市场总体变量，包括市场占有率、营销行为、混合营销策略等对创新扩散的影响，主要代表是BASS模型及其衍生模型[6]。微观创新扩散模型主要从潜在的采纳者对创新采纳的微观层面的影响，基于微观的创新扩散研究模型认为潜在采纳者需要通过决策来决定是否采用创新，扩散模型重点在于考察创新扩散的规律和程度[7]。随着复杂网络技术的发展，基于复杂网络的创新扩散逐渐成为研究重点：Cowan等年基于复杂网络模型讨论了创新扩散和网络结构之间的关系，提出了基于复杂网络的知识扩散模型[8]。Andre等从复杂网络出发，构建扩散模型，并使用计算机仿真分析方法分析了知识、创新在网络中的扩散过程[9-10]。李志宏等研究探讨了网络中成员的特征关系长度和聚类系数对知识扩散的影响[11]。

传统的宏观和微观扩散模型难以解释在创新网络中技术创新的扩散行为和特征,而目前复杂网络上的创新扩散研究主要基于小世界网络、无标度网络等理想条件下的复杂网络模型，对于真实网络结构中的技术创新扩散研究相对较少。因此，本文在已有研究的基础上，基于真实数据创建合作专利创新网络并分析其结构特征，以创新网络作为创新扩散载体，结合传播动力学的相关理论和方法，构建企业集群中技术创新扩散模型。通过采用计算机仿真方法，分析和探索在企业集群技术创新扩散模型中网络结构、网络规模、节点属性和感染强度等因素对技术创新扩散的影响，为政策制定提供有益的借鉴。

1　企业专利合作关系的创新网络构建和分析

1.1　创新网络构建

在创新过程中企业主体由于受自身的研发能力、交易成本、管理水平等因素的影响，通常会自愿或者以其他互动方式构建协作研发网络。从网络视角来看，企业主体之间的知识、创新技术会随着主体间互动关系而发生流动，而创新主体之间通过互动关系形成的网络就是创新技术扩散的基础。作为衡量高新技术企业技术创新能力的重要指标，专利数据包含了关于技术创新发展和创新活动相关的各种有价值的信息。因此，本文在构建基于合作专利创新网络的基础上，研究技术创新扩散过程。

作为新兴的先进生产力代表，互联网技术是培育经济的新动力和新引擎，为传统企业转型升级提供了平台和技术支持；传统企业与互联网技术深度融合，可以更快速和高效地促进企业的转型升级。因此，本文以企业作为创新主体，研究基于企业关于互联网的专利联合申请数据构成的创新网络中技术创新扩散过程和规律。

根据复杂网络相关理论，网络拓扑结构可表示为G=(V,E)，V表示网络中节点或者顶点的集合，E为边的集合，表示顶点之间的连接关系[12]。根据上述定义，本文将V定义为创新网络中企业个体的集合，E定义为联合申请专利中企业个体关系的集合，利用联合申请专利数据构建企业基于专利合作关系的创新网络。

1.2　数据来源

本文的数据来源于“中国专利数据库”，在“中国专利数据库”对企业基于互联网进行创新发明的专利数据进行检索。步骤如下：①设置专利关键字包含“互联网”；②在获得初步的搜索结果以后，过滤申请者为个人的数据，仅保留申请人为公司的专利数据；③随后对数据再次进行筛选，保留专利申请人为至少两个以上的公司、企业、研究所。近年来，互联网成为最为活跃的创新领域之一，基于互联网创新的专利数据明显增加。企业间的联合创新互动更为活跃，合作创新网络结构也越来越复杂。为了更明显地体现这种变化趋势，本文选取2008年企业合作创新网络和2015年企业合作创新网络进行分析。

本文使用UCINET软件，基于上述合作专利数据，分别构建了如图1和图2所示的企业合作创新网络。从网络拓扑结构来看，基于2015年合作专利数据的创新网络相对于2008年数据的创新网络，网络结构由松散转向集聚，并且存在明显的大度节点。

图1　基于2008年合作专利数据的创新网络

图2　基于2015年合作专利数据的创新网络

1.3　合作创新网络结构分析

与规则网络和随机网络不同，真实网络具有明显不同于前述两者的统计特征[12]。通常情况下，真实网络也被称为复杂网络。在复杂网络中，最明显特点就是复杂网络通常具有无标度特性和小世界性。已有研究表明，网络是否是无标度网络、是否具有小世界网络的特性,可以从网络中节点的度分布、平均路径长度以及网络的聚类系数这三个指标进行判断[13]。

大量已有的研究表明，与规则网络相比，复杂网络的节点度服从明显的幂率分布[12,14-15]。网络节点的度分布函数为P(k)，表示任意选择的节点恰好有k条边的概率，等于网络中度数为k的节点的个数与网络节点的总数的比值[16]。

图3为基于2015年合作专利数据的创新网络中各节点的累计度分布曲线图,从图中可以看出,合作创新网络的度分布服从明显的幂率分布，且下降幂指数为1.13，即P(k)=k-1.13,度分布曲线表明合作创新网络具有较为明显的无标度特征，说明在合作创新网络中存在明显的大度节点。

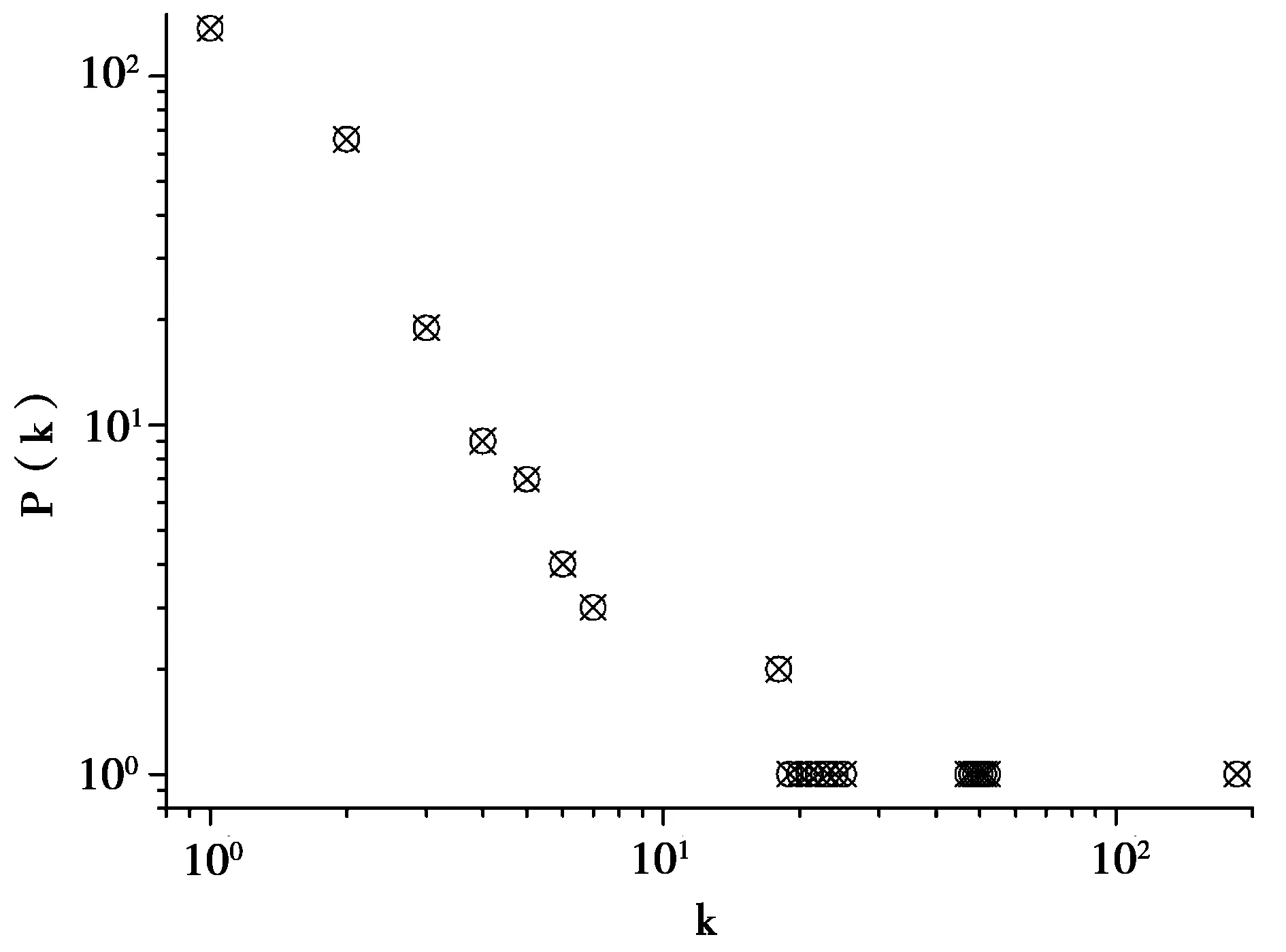
图3　合作专利网络的度分布

在网络中平均路径长度表示为所有节点对距离的平均值，而聚集系数主要用于衡量网络中节点的聚集程度，主要用于表示网络的密度和连通性。已有研究表明，随机网络具有较大的聚类系数和较大的平均路径，而小世界网络具有较短的平均路径长度和较大的聚类系数[17]。

聚类系数C的取值范围为[0～1]，当C=0时，表示网络中所有节点均为孤立离散的节点，而C=1时，表示网络中所有节点都互相连接。聚类系数越大，表明网络中节点之间的合作关系越紧密[16]。

通过计算，本文构建的2008年合作创新网络平均路径长度为2.618，2015年网络的平均路径长度为1.835。在2015年的合作创新网络中，由于存在较短的平均路径长度，各节点间能以更快的速度和更低的交流沟通成本进行知识扩散和传播。2008年的创新网络的聚类系数为0.394，2015年为0.785，不同的聚类系数说明2015年网络中各节点间的关联性在加强，合作关系更加紧密，有利于知识和技术扩散。

合作创新网络具有较短的平均路径长度和较大的集聚系数，较短的平均路径长度保证网络中个体能以较低的成本互相获取知识或接收新的技术；较高的集聚系数保证节点间的合作关系更为紧密，有利于技术创新在网络中快速扩散。此外，网络的度分布服从幂率分布，具有无标度网络的特征，合作创新网络中的大度节点和Hub节点加速了技术创新扩散的速度。

2　复杂网络背景下企业集群技术创新扩散模型

2.1　企业集群技术创新扩散过程

在经济社会的不同环境中都有扩散现象的发生，虽然产生扩散的原因、扩散行为的载体不同，但这类扩散现象的本质可用“传染”模型进行描述[18]。本文以传染病传播模型(SIR)的基础构建技术创新扩散模型，研究技术创新扩散过程和规律。首先对企业集群技术创新扩散过程做出以下假设：

(1)企业组成的创新产业集群是一个相对开放的环境，企业进入和退出不依赖于创新的扩散过程，仅与企业自身情况有关。假定在某个时间段内进入和退出的企业均相等，企业集群数量将稳定为常数N。企业通过合作研发行为形成创新网络，网络中的节点表示企业个体，节点和节点之间边表示企业之间的关于技术创新的合作行为。

(2)每个企业在集群中存在三种状态：“缺乏创新能力”状态S，表示不具备某类技术创新，但时刻准备通过合作研发的方式来获取掌握该技术创新；“具备创新能力”状态I，表示已掌握并在企业运营中熟练应用某类技术创新，同时企业也有意愿以合作的方式将该技术创新转让给其他处于S状态的企业；“升级创新能力”状态R，表示处于I状态的企业从实际情况出发，将转向更高层次技术创新的攻关和研究。企业一旦转变为R类，则该企业将会退出本轮的创新扩散过程，失去对创新或知识的传播能力。同时，定义在t时刻，S(t)、I(t)、R(t)分别表示上述三类企业个体的概率密度。

在完成上述假设的基础上，结合传统的SIR模型，企业集群技术创新扩散过程可以进行以下描述：节点i处于S状态且与处于I状态的节点j相连，则处于S状态的节点i转换为I状态的概率为φ(i)。同时规定，处于I状态的节点j在下一个时间步将以一定的概率转换为“升级创新能力状态”R。其中，φ(i)=pwijβ，wij为节点i、j之间边的权重，β为感染率，p为创新扩散的感染强度。

在现实网络中，感染强度p通常与市场机制、政策等影响因素相关。在市场机制的影响下，感染强度通常与企业接受创新扩散的成本(采纳创新技术后设备、技术、人力方面的投入)以及企业接受创新扩散后增加的收益相关；同时，从政策影响来看，对于不同的行业政策支持的力度不同，例如对于传统制造业，由于正处于转型升级的关键时期，对于关键设备、关键技术可能需要依赖于国外进口，为了加速企业的转型升级，政府可能会从政策上对于这类企业进行支持(补贴、税收、惩罚力度)，激励和引导这类企业加速接受和采纳创新技术。为简化考虑，本文在后续的研究中将市场机制和政策影响等因素统一定义为感染强度p。

2.2　基于复杂网络环境的企业集群创新技术扩散模型

在对企业集群创新技术扩散过程进行定义以后，为了进一步在企业合作创新网络中研究技术创新扩散过程和规律，可根据平均场理论，构建企业技术创新扩散模型[19-21]：

S(t)=e-λkφ(t)

(1)

在式(1)中：

(2)

将式(2)对t求导可得：

(3)

又因为S(t)+I(t)+R(t)=1，将式(1)(2)带入式(3)可得：

(4)

(5)

要得到式(5)的非零解，需满足：

(6)

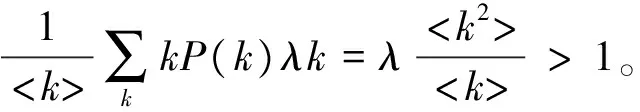
(7)

对于度分布函数为P(k)=k-γ，γ≤3的网络，有=∞[10-12]。企业合作专利创新网络的度分布为P(k)=k-1.13，因此无论设置的传染概率多小，创新合作网络中创新扩散都会存在。

3　实验过程与结果分析

企业合作专利关系形成的创新网络具有小世界性网络的特点，同时也具备无标度网络的特性。为了确定企业集群中技术创新扩散影响因素，本文通过Matlab仿真实验的方式，讨论网络结构、节点属性、网络规模、感染强度等参数变化对技术创新扩散的影响。仿真实验所涉及的网络类型包括随机网络、小世界网络、无标度网络和实际的创新网络。随机网络基于ER随机网络模型生成，无标度网络基于BA无标度网络模型生成，小世界网络基于SW小世界网络模型生成。

3.1　不同的网络结构对创新扩散过程的影响

在随机网络、小世界网络和无标度网络上进行创新扩散过程仿真时，为了更客观地体现技术创新在不同网络结构中的扩散情况，首先将不同类型网络的基本参数都设置为相同。其中，网络节点的数量N=497，网络节点的平均度d=4，感染率设置为λ=0.025，感染强度p=1。为了更清楚地显示创新活动在创新网络中的扩散，本文引入扩散比例φ(t)=I(t)/N，用于描述创新活动扩散的范围。

在每种类型网络随机选取一个节点Si，修改其状态为Ij。在参数固定的情况下，进行200次独立的扩散实验。实验结束以后取处于I状态个体数量的均值，可得到如图4所示的不同网络下技术创新扩散规律。

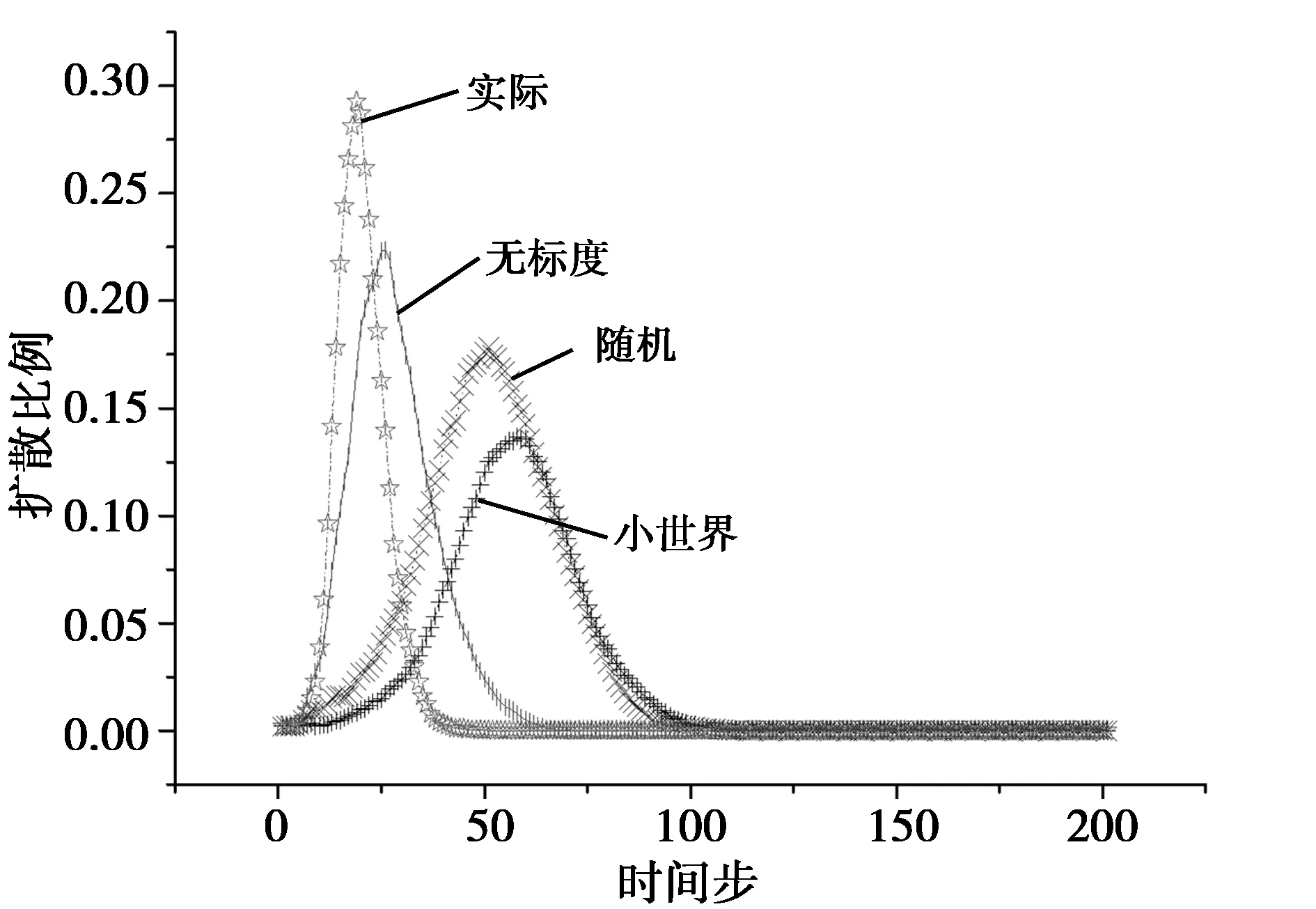
图4　不同网络结构创新扩散过程

通过对创新扩散模型中创新活动扩散比例变化曲线进行分析，可以看出，在三种理想的网络模型中，无标度网络中创新的扩散速度和规模都要大于随机网络和小世界网络。但是与实际网络相比，实际网络的传播速度和扩散范围大于无标度网络，其主要原因是Hub节点强大的传播能力。

为了考察技术创新与节点属性间的关系，在参数固定的情况下，分别选取最大度节点和度为1的随机节点独立进行了200次实验。对实验结果取均值，得到图5所示的节点属性与创新扩散的关系。图5的大图为技术创新从最大度节点发起的情况，小图为创新扩散从最小度发起的情况。

图5　最大度和最小度扩散

从图4和5可以看出，创新技术扩散无论由随机节点、最大度节点发起或者由最小度节点发起，都会在网络中进行传播，节点的属性仅仅只影响扩散的速度和程度，不会影响阻止网络中的技术创新的扩散过程。

3.2　感染强度对创新扩散过程的影响

为了研究感染强度对技术创新扩散过程的影响，在网络结构参数固定的情况下，分别设置感染强度p为0.3、0.5、0.7、0.9，在不同的感染强度下进行独立的200次仿真实验，实验结果如图 6～9所示。从图中可以看出，在实际网络、无标度网络中，感染强度不会影响创新行为扩散的过程，感染强度的变化仅仅只对创新行为扩散的速度和范围造成影响。这与创新扩散的阈值λc有关，在无标度网络或真实的创新合作网络中，λc->0[15]，在这两种网络中，只要存在状态为I的个体，技术创新就会进行扩散。但是对于小世界网络和随机网络，当感染强度小于0.5时，将会影响小世界网络中创新行为的扩散，而在随机网络中，感染强度低于0.5时，创新行为的扩散过程和扩散范围明显低于感染强度为0.7和0.9的情况。图10～12详细展示了不同感染强度下四种网络结构的创新技术扩散情况。

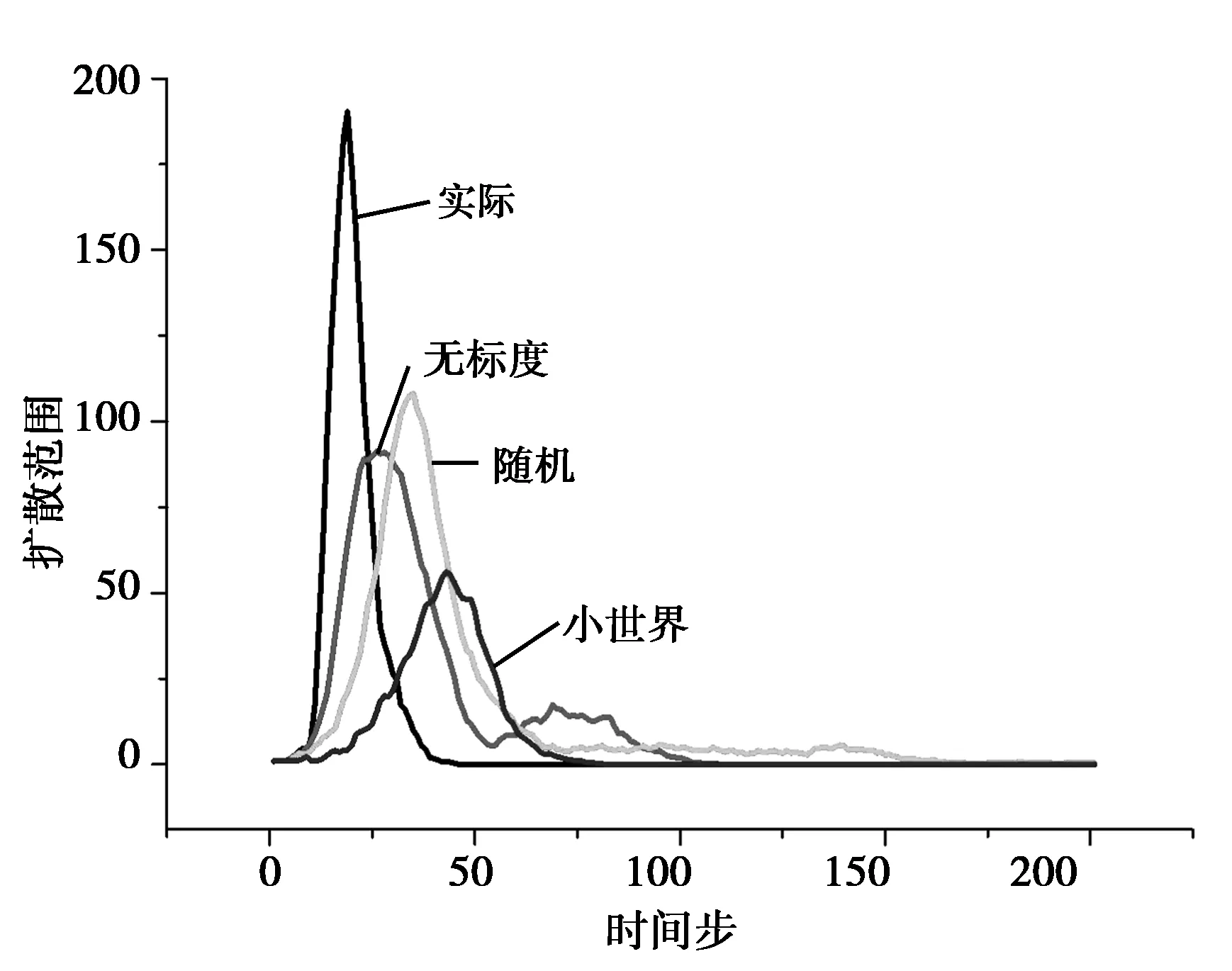
图6　p=0.9的扩散过程

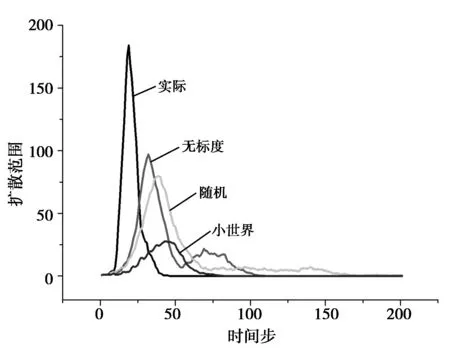
图7　p=0.7的扩散过程

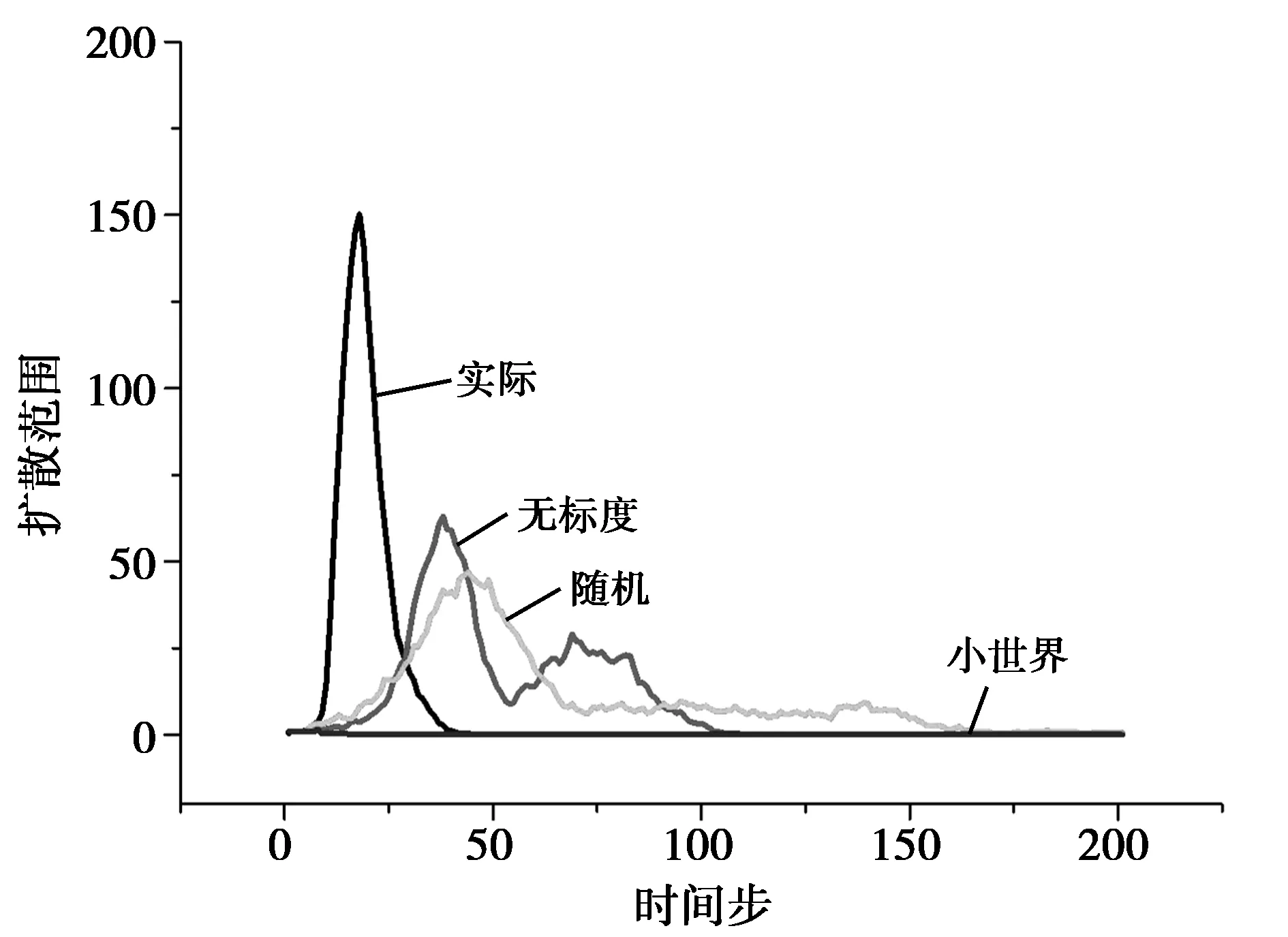
图8　p=0.5的扩散过程

3.3　网络规模对创新扩散过程的影响

上述讨论和实验均是在网络中节点数量固定的情况下进行的，但在真实创新网络结构中，网络的规模是不断变化的，随着节点的加入和退出网络规模将会发生一定的变化。由于数据获取原因，本节中只选取在无标度网络、小世界网络、随机网络三种网络结构进行仿真。网络节点的数量设置范围为50、100、200、400、800、1600，设定感染强度p=1。

为了更精确地测量扩散速度，本文参考文献22的方法，引入扩散时间尺度(Scale)描述创新在网络中扩散的速度，扩散时间尺度T定义为：

(8)

式中，t表示时间步，NI(t)表示在t时刻处于I状态的个体数量。T值反映了创新扩散的速度，T越小表明创新扩散速度越快。

图9　p=0.3的扩散过程

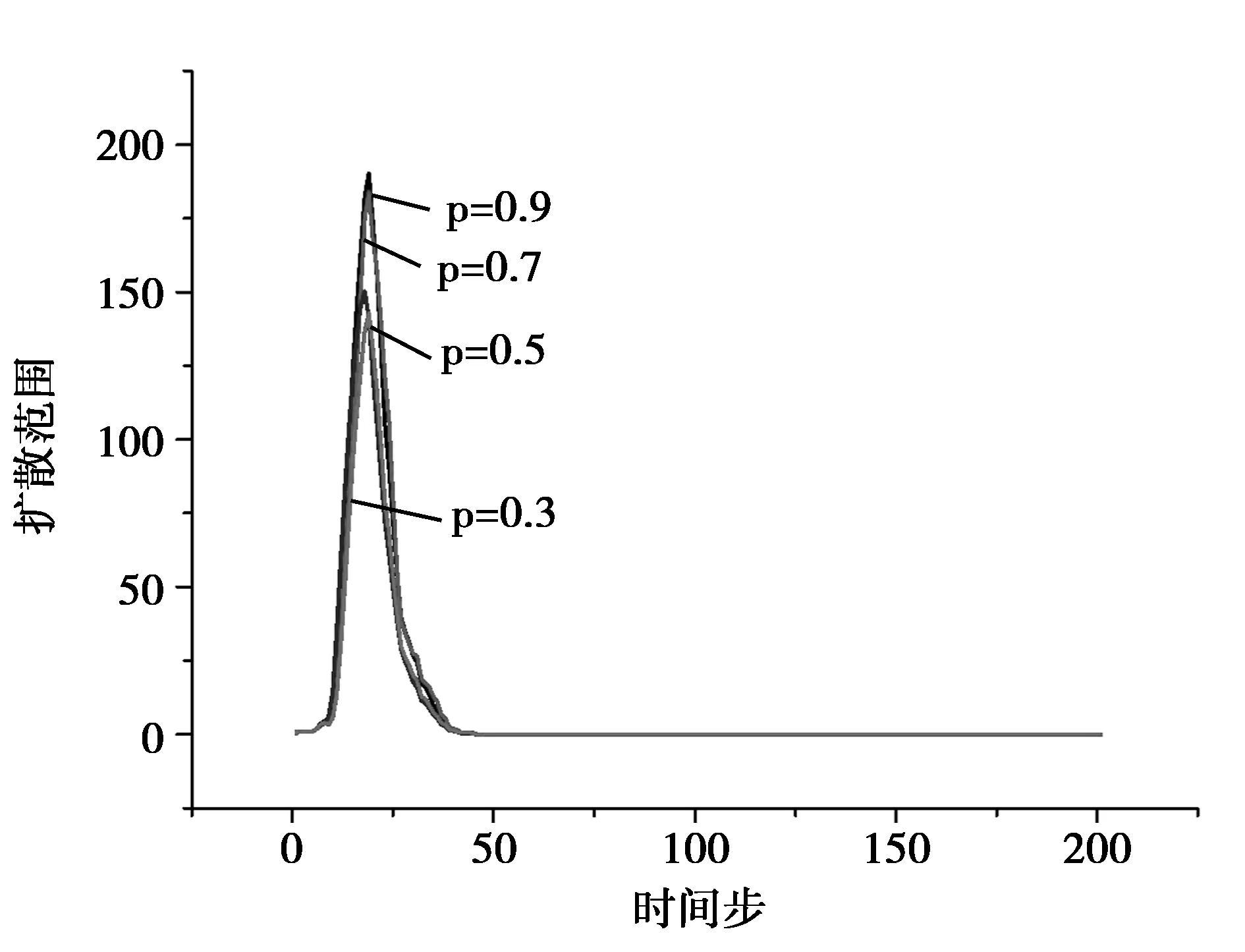
图10　实际网络中不同感染强度下的创新扩散

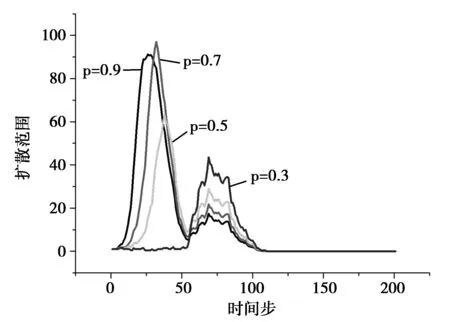
图11　无标度网络中不同感染强度下的创新扩散

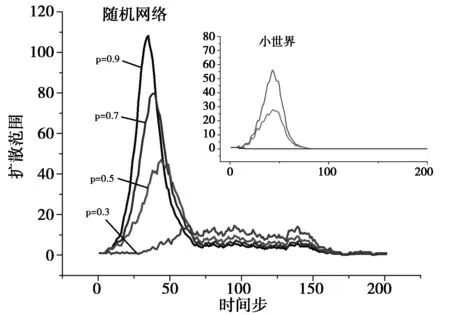
图12　小世界网络和随机网络创新扩散过程

在固定网络参数的情况下，通过独立的100次实验，可以得到技术创新扩散与网络规模之间的关系，实验结果如图13～15所示。

从不同规模网络的创新扩散过程来看，创新扩散尺度随着网络规模的扩大而增加。但在无标度网络中，由于大度节点和Hub节点强大的转发作用，网络规模对创新扩散速度影响较低。因此，可以增加具有无标度网络特性的网络中大度节点和Hub节点的支持力度，以确保技术创新在网络中的快速传播。

4　结论与展望

本文从构建企业集群基于合作专利的创新网络出发，探讨了企业集群中创新技术的扩散过程和规律。研究表明：创新网络具有较大的聚类系数和较小的平均路径长度，较高的聚集系数意味着网络中节点间的关系更为紧密，而较短的平均路径长度则标志着节点之间能以较低的成本完成信息传递。同时，从创新网络的度分布曲线来看网络具有无标度性，网络中存在的大度节点，对于提升企业集群整体竞争力起着极其重要的作用。通过对创新技术扩散的影响因素研究，得出以下结论：①网络结构和网络规模都会对创新扩散过程产生影响，真实的网络由于具有小世界网络和无标度网络的特点，有利于技术创新的快速扩散和传播；②感染强度会影响创新行为的扩散速度和扩散范围，通过对感染强度的控制，可以提高创新扩散的速度和增大其影响范围。通过实验可以看出，本文所建立的基于企业合作专利关系的技术创新扩散模型具有一定的通用性，对研究企业集群中技术创新扩散规律具有一定的理论价值和意义。如何将感染率和感染强度与企业内部因素以及市场、政策因素相结合，预测技术创新扩散路径，将是下一步的研究重点。

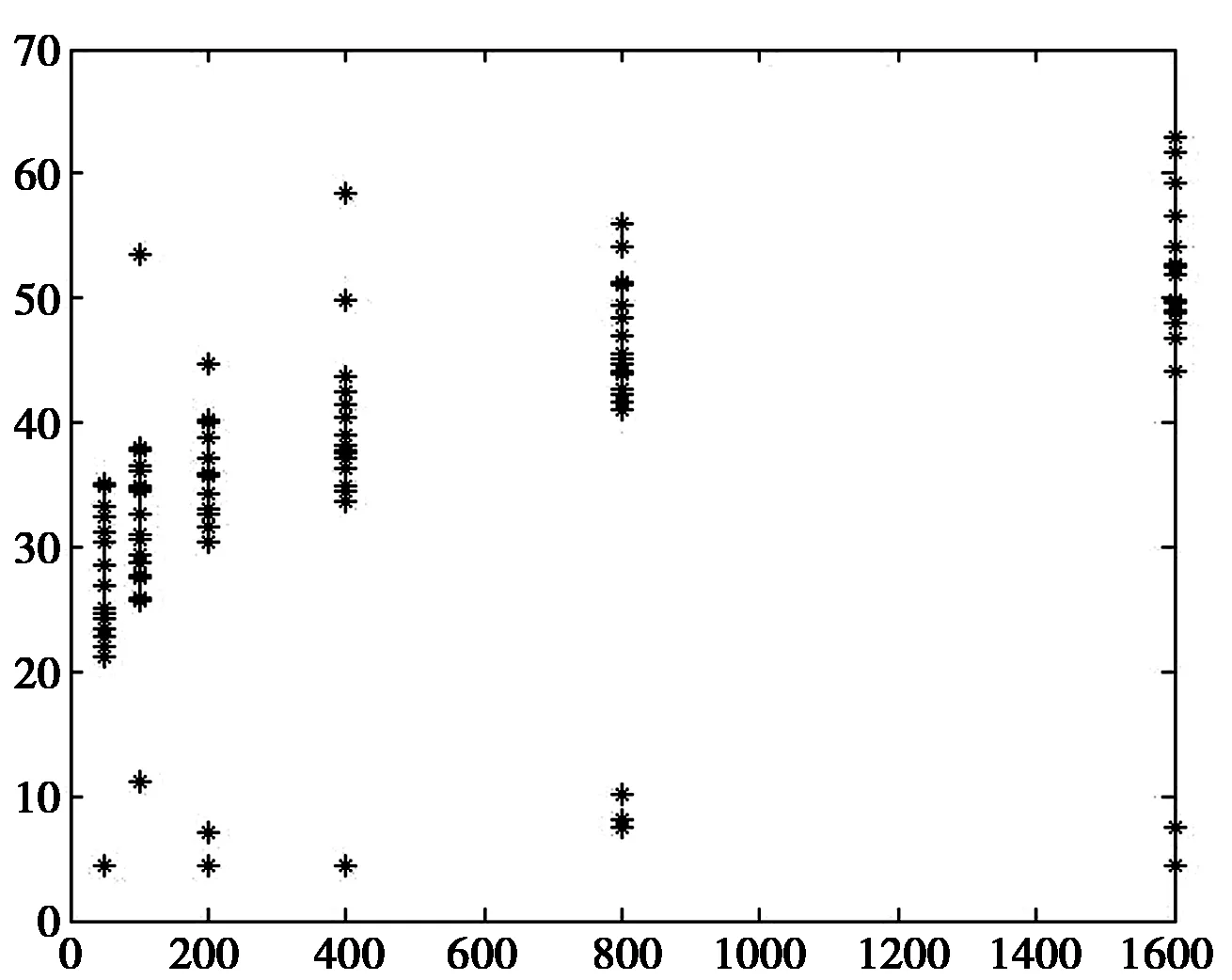
图13　随机网络

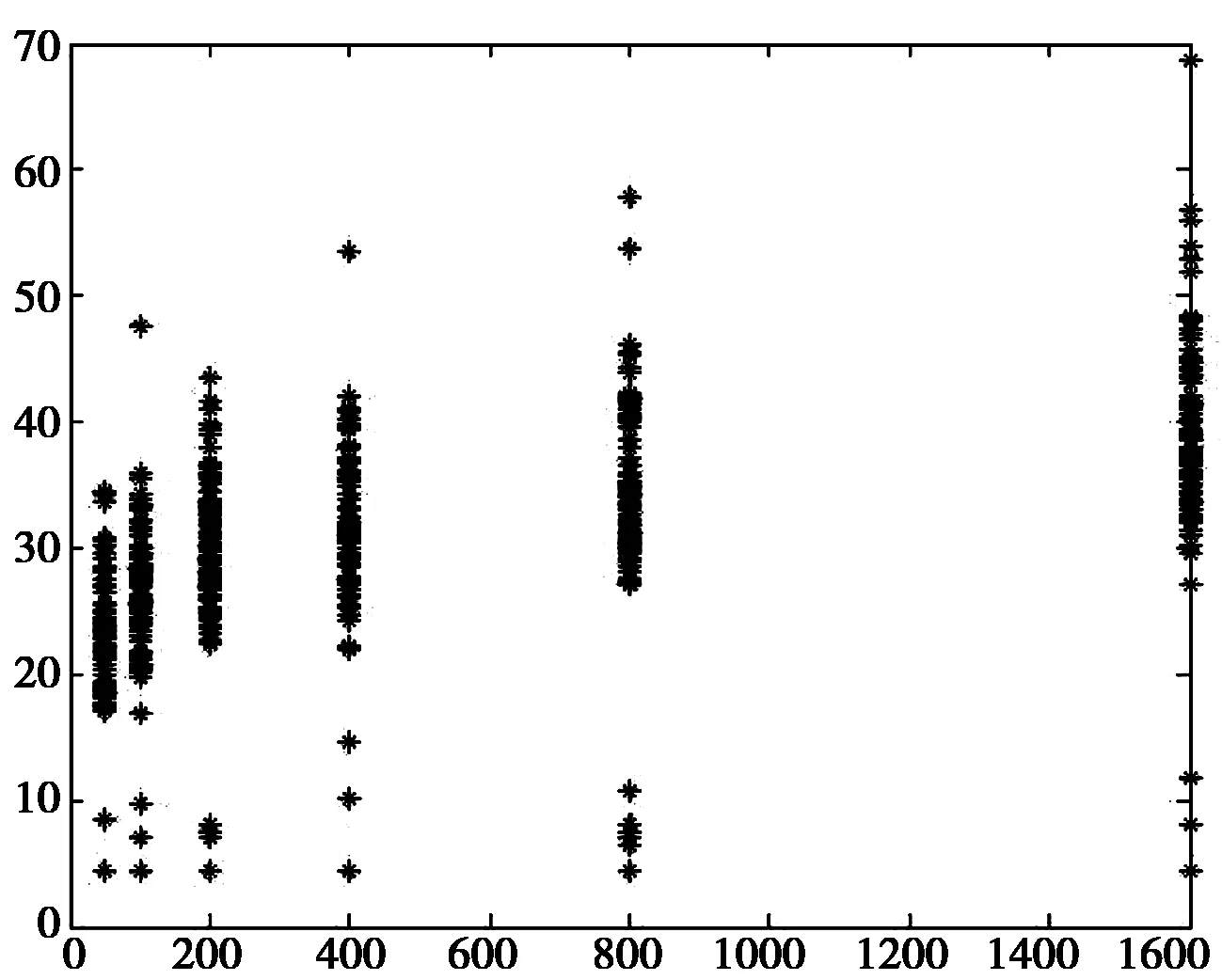
图14　无标度网络

图15　小世界网络

参考文献：

[1]雷志梅,王延章,司雨昌.基于知识的产业关联网络模型分析[J].系统工程,2014(12):46-54.

[2]董慧梅,侯卫真,汪建苇.复杂网络视角下的高新技术产业集群创新扩散研究——以中关村产业园为例[J].科技管理研究,2016,36(5):149-154.

[3]王珊珊,王宏起.技术创新扩散的影响因素综述[J].情报杂志,2012(06):197-201.

[4]陈国宏,王丽丽,蔡猷花.基于Bass修正模型的产业集群技术创新扩散研究[J].中国管理科学,2010(05):179-183.

[5]李永周,桂彬,姚婳,等.基于网络组织的国家高新区企业创新能力评价研究[J].中国科技论坛,2008(8):63-67.

[6]赵维双,刘涛.基于技术创新扩散环境的Bass扩散模型修正研究[J].经济问题,2008(12):67-69.

[7]华锦阳.技术创新扩散决策模型:综合回顾及新模型构建[J].科技进步与对策,2015(5):5-10.

[8]COWAN R,JONARD N.Network structure and the diffusion of knowledge[J].Journal of economic dynamics & control,2004,28(8):1557-1575.

[9]ANDRE,et al.An opinion dynamics model for the diffusion of innovations[J].Physica A,2009,388:3225-3232.

[10]于同洋,肖人彬,龚晓光.组织网络隐性知识扩散及学习策略分析[J].管理科学,2009,22(6):21-28.

[11]李志宏,朱桃.基于加权小世界网络模型的实践社区知识扩散研究[J].软科学,2010,24(2):51-55.

[12]NEWMAN M E J.The structure and function of complex networks[J].Siam review,2003,45(2):167-256.

[13]ALBERT R Barab’asi.Statistical mechanics of complex networks[J].Rev.mod.phys,2002,74(1):2002.

[14]WATTS D J,STROGATZ S H.Collective dynamics of‘small-world’networks[J].Nature,1998,393(6684):440.

[15]周涛,傅忠谦,牛永伟,王达,曾燕,汪秉宏,周佩玲.复杂网络上传播动力学研究综述[J].自然科学进展,2005(5):513-518.

[16]汪小帆，李翔，陈关荣.复杂网络理论及其应用[M].北京：清华大学出版社,2006.

[17]BARABASI A L,ALBERT R.Emergence of scaling in random networks[J].Science,1999,286(5439):509.

[18]陈柏彤,张斌.产业集群知识扩散动态演化分析[J].情报科学,2016,34(9):150-154.

[19]倪顺江.基于复杂网络理论的传染病动力学建模与研究[D].北京：清华大学,2009.

[20]李光正,史定华.复杂网络上SIRS类疾病传播行为分析[J].自然科学进展,2006(04):508-512.

[21]李恒毅.基于系统动力学模型的创新网络技术扩散模拟仿真研究[J].系统工程,2014(03)：87-91.

[22]廖列法,孟祥茂.复杂网络上具有多感染阶段的传染病传播模型[J].计算机应用,2014,34(11):3254-3257.