K-近邻矩阵分解推荐系统算法

郝雅娴，孙艳蕊

(东北大学 理学院，沈阳 110819) E-mail：Hao_yaxian@163.com

1 概 述

近几年来，随着Internet的发展以及电子商务网站迅速崛起，推荐系统[1]广泛应用于电子商务网站，为网站用户进行商品智能推荐，大大提高了电子商务网站的商业效益.因此，如何提高推荐算法的推荐结果准确性成为电子商务网站的目标追求.协同过滤算法[2]是目前应用最广泛且效果最好的推荐系统算法.但是，随着电子商务网站不断增加的用户量与商品量，大数据下导致的数据稀疏性使得协同过滤算法已经远远不能正确对用户的评分值做出准确的预测.所以，在协同过滤算法基础上进行改进的算法不断出现.例如：基于项目的协同过滤算法及其算法改进[3-5]，基于神经网络的协同过滤算法[6]以及基于矩阵降维的协同过滤算法[7，8]，基于邻域的协同过滤算法改进[9]等.

本文算法是在基于邻域的协同过滤算法与基于矩阵分解的协同过滤算法[10]两方面基础上提出的.主要贡献是解决了大数据导致的极大稀疏性问题，并且能很好的找到与目标用户对目标项目的评分相关性较大的用户与项目，使得评分值更加精确，算法主要包括三个方面的内容：一、分别对目标用户u与目标项目i寻找其最近邻，这一部分在4.2与4.3详细给出，二、建立近邻矩阵并对近邻矩阵进行矩阵分解，三、预测评分值，二、三部分在4.4中给出.

2 传统的矩阵分解

2.1 矩阵分解模型

矩阵分解算法具有伸缩性好，灵活性高等特点.最早的矩阵分解算法为奇异值分解算法(Singular Value Decompostion，SVD)，但是SVD有两方面的缺点：一是在算法执行之前必须补全原始评分矩阵中的缺失值；二是算法执行效率太低.在SVD算法之后Simon Funk将随机梯度下降算法应用在推荐算法中，他利用随机梯度下降算法高效的实现了评分值的预测.此后，利用随机梯度下降算法的矩阵分解被应用于各大电子商务网站，成为了经典的推荐系统算法.

Simon Funk提出的矩阵分解算法是将用户与项目映射到隐语义空间上，因此该算法也被称作隐语义模型.以电影为例，影响用户对电影评分值的隐语义可能是电影的类型：悲剧、喜剧、爱情片等等.矩阵分解算法进行商品推荐的前提是对原始评分数据矩阵的学习，设原始评分矩阵有m个用户，n个项目，记原始评分矩阵为Rm×n=(rui)m×n.f表示隐语义的个数.每个用户u对应一个隐语义向量(用户因子向量)pu∈Rf，每个项目i对应一个隐语义向量(项目因子向量)qi∈Rf.算法通过将用户因子向量与项目因子向量做内积来对未知评分项做预测[10].

(1)

2.2 随机梯度下降算法

(2)

1)已知rui-qTpu～N(0，δ2)

3)最大化p(rui)，等价于最大化lnp(rui)，由(2)得：

4)观察lnp(rui)可知，在等式右边的两项中，只有∑∑(rui-qTpu)2为变量，所以最大化lnp(rui)，等价于最小化∑∑(rui-qTpu)2.

(3)

(4)

(5)

其中γ控制迭代的步长，不宜太大，通常利用交叉验证得到.通过等式(4)的计算分别得到项目因子向量(6)与用户因子向量(7)参数更改的定义式[10].

qi=qi+γ·(eui·pu-λ·qi)

(6)

pu=pu+γ·(eui·qi-λ·pu)

(7)

利用随机梯度下降算法得到能够使等式(3)最优的参数qi∈Rf与pu∈Rf，从而得到预测评分值.Simon Funk提出的矩阵分解算法提高了算法的执行效率，但是在大数据背景下，这一经典算法已经不能够很好的反映原始数据的真实性，因为原始评分矩阵极大的稀疏性对实验结果准确造成很大影响.所以在该算法上建立了很多混合算法与改进算法来提高推荐结果的准确性.本文提出了一个基于矩阵分解与最近邻的混合协同过滤算法，该算法充分利用了矩阵分解算法与最近邻算法的优点，实验证明本文算法有较好的推荐效果.

3 传统的最近邻算法

基于最近邻算法(K-Nearest Neighbor algorithm，KNN)是最常用的协同过滤算法，最先提出的是基于用户的协同过滤算法[12].其基本思想是利用目标用户近邻用户的评分值去估计目标用户对项目的评分预测值.随后基于项目的最近邻算法被提出[13，14]，因为基于项目最近邻算法比基于用户最近邻算法具有更好的合理性与高效性，被广泛应用.在这里只介绍基于项目最近邻算法的基本思想，对于目标项目i的最近邻寻找，首先定义最近邻个数k，将计算所得的相似度按从大到小的顺序排列，选取前k个作为目标项目i的k个最近邻用户.寻找项目最近邻算法的关键问题是通过计算相似度来寻找最近邻，计算相似度的方法常用的有欧氏距离、余弦相似度以及皮尔逊相似度，本文采用欧氏距离方法计算相似度，计算公式如下：

(8)

公式(7)中的i与j分别表示原始评分矩阵中的任意两个项目，Ri与Rj分别表示项目i与j对应的评分向量，Sij表示项目i与j之间的相似度大小.将计算所得的相似度大小保存到相似度向量矩阵中，预测评分值由评分值与相似度的加权平均值得到，记Nk(i；u)为项目i的最近邻集合，j∈Nk(i;u)表示用户u评过分的项目i的近邻项目j[11]则：

(9)

基于最近邻算法是最早期的协同过滤算法，当在原始评分矩阵具有极大的稀疏性时，利用相似度计算目标项目的最近邻会出现误差.因此许多学者在KNN算法执行之前会首先对原始评分矩阵进行预处理，从而使算法的准确性提高.本文在对原始数据处理之后，同时对目标用户与目标项目查找最近邻，并建立近邻评分矩阵，对新的评分矩阵进行矩阵分解，实验证明本文算法提高了推荐结果的精确度.

4 K近邻矩阵分解算法

为了更好的解决原始评分矩阵稀疏性与推荐结果的准确性，许多学者建立了协同过滤算法的混合型算法，例如Yehuda Koren等人提出的混合算法[14].本文在最近邻算法与矩阵分解算法的基础上提出了一个新的混合算法——K近邻矩阵分解算法，(A K-Nearest Neighbor Matrix Factorization for Recommender systems)简称KNNMF.

4.1 初始化评分矩阵

因为原始评分矩阵极大的稀疏性，会影响算法实验结果的准确性，所以在算法执行之前首先对原始评分矩阵进行初始化，本文采用文献[14]中的公式(10)对原始评分矩阵进行数据预处理.

(10)

图1 k=2时RMSE随参数α、f的变化分布Fig.1 DistributionofRMSEwithα、fbasedonk=2图2 k=5时RMSE随参数α、f的变化分布Fig.2 DistributionofRMSEwithα、fbasedonk=5

图3 k=7时RMSE随参数α、f的变化分布Fig.3 DistributionofRMSEwithα、fbasedonk=7图4 k=10时RMSE随参数α、f的变化分布Fig.4 DistributionofRMSEwithα、fbasedonk=10

5,7,10，固定f，参数α的改变对RMSE的值影响不大，如图1-图4.因此本文取α=500作为实验数据量(见图1-图4).

4.2 基于用户最近邻计算

本文算法首先计算用户最近邻，针对目标用户u寻找其前k个最近邻，v∈Nk(u;i)表示对商品i评过分的用户u的近邻用户v，建立用户u的近邻集合U={v|v∈Nk(u;i)}.例如表1给出了五个用户对五个商品的评分情况，如果计算用户User3对目标项目Item1的评分(在这里取k=2).需首先寻找对项目Item1评过分的用户，即表1中User1,User2,User3，利用欧氏距离计算目标用户与以上用户之间相似度分别为：S13=2.2361，S23=5.8130，S53=4.5826.由欧氏距离的大小可知User1与User5为目标用户User3的k最近邻用户，此时目标用户的近邻集合U={User1,User5}.

表1 用户-商品评分矩阵Table 1 Users- items rating matrix

4.3 基于项目最近邻计算

将目标用户k的最近邻保存于集合U中，接下来对目标项目i寻找其前k个最近邻，j∈Nk(i；u)表示用户u评过分的项目i的近邻项目j，建立项目i的近邻集合J={j|j∈Nk(i;u)}.计算表1中用户User3对目标项目Item1的评分(在这里取k=2)，首先寻找用户User3评过分的项目，即表1中Item2，Item3,Item4,Item5利用欧氏距离计算目标项目与以上项目之间的相似度，分别为S12=3.4641，S13=6.7832，S14=6.4807，S15=5.6569.显然Item2与Item5为目标项目Item1的k最近邻用户，此时目标项目的近邻集合J={Item2,Item5}.

4.2与4.3主要计算目标用户与目标项目的前k个最近邻，并将计算所得的目标用户与目标项目的最近邻分别保存到目标用户近邻集合U={v|v∈Nk(u;i)}与目标项目集合J={j|j∈Nk(i;u)}，在数据集中，每一个用户与项目均有最近邻，所以可以得到用户近邻矩阵UKm×k=[U1,U2，…，Um]T与项目近邻矩阵JKn×k=[J1,J2,…,Jn]T.用户近邻矩阵与项目近邻矩阵为接下来建立近邻评分矩阵做准备.

4.4 矩阵分解与评分预测

预测评分值rui，目标用户u的k最近邻对目标项目i的k最近邻的评分值构成的矩阵，称为近邻评分矩阵，记为KR，则

这是一个k阶方阵，rviji表示目标用户近邻对目标项目近邻的评分值，其中vi∈U，ji∈J，I=1,2,…,k.

例如在4.2的例子中，要预测User3对目标项目Item1的评分，根据定义可以建立如下近邻评分矩阵.本算法提出的近邻评分矩阵有效的提取了目标用户对目标项目评分值相关性最大的近邻用户与近邻商品的信息，从而降低了稀疏性对实验结果的影响，提高了算法的推荐精度.

DRk×k=PQT

(11)

本文提出了计算未知评分值rui的新方法.在公式(11)中，|DRk×k|表示矩阵DRk×k的行列式值，行列式的值是矩阵特征值的乘积，特征值反映了矩阵本身的性质.因为每一个用户与项目作为目标用户与目标项目的最近邻的概率均为1/k，所以rui的值由分解之后矩阵的行列式值乘以1/k.

(12)

对矩阵KR进行分解时需要考虑因子个数对推荐准确度的影响.本文以MovieLine数据集为实验数据，在参数α=500的条件下，寻找矩阵分解实验的最优隐因子个数f，如图5，图中iterlatent为隐语义个数f，通过实验可知，当因子个数为5与2时推荐结果的准确度几乎相近.所以当因子个数取5与2时，推荐结果是最好的，从而下面的实验中均取f=5.

5 实验结果与分析

5.1 评价标准

本算法利用均方根误差(RMSE)验证实验结果的准确性，以RMSE值作为实验准确性的评价指标，RMSE的值越小算法实验结果越优.计算公式如下：其中TestSet表示测试集[15].

(13)

5.2 实验结果

本文实验所采用的数据集为MovieLens数据集，MovieLens数据集是包含943个用户与1682部电影的评分矩阵.本文算法与三种算法进行比较：

图6为本文提出的K近邻矩阵分解算法(K-Nearest Neighbor Matrix Factorization，KNNMF)与原始矩阵分解算法(Matrix Factorization，MF)的实验结果对比图，由图可知，对k=2,5,7,10时，随着隐因子个数的变化，KNNMF算法所得的RMSE值低于MF算法的RMSE值，所以本文算法的实验结果更加精确.

图5 RMSE随参数的f变化分布Fig.5 DistributionofRMSEwithf图6 原始矩阵分解与K近邻矩阵分解算法RMSE比较Fig.6 RMSEcomparisonofmatrixfactorizationandKNNMF

图7为本文提出的KNNMF算法与Y.Koren等人提出的联合近邻插值算法[14]的实验结果对比，由图中数据可知，取相同的k近邻时，本文算法KNNMF的RMSE值远远的小于KNNw的RMSE值，所以，本文算法极大的提高了推荐结果的精确度.

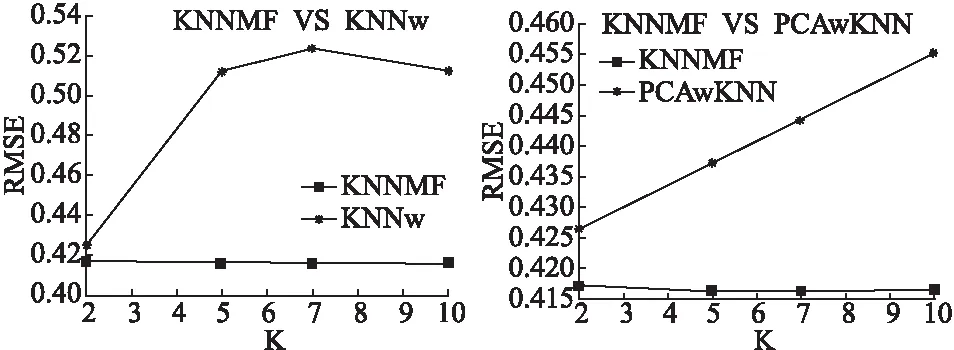
图7 联合近邻插值算法与K近邻矩阵分解算法RMSE比较Fig.7 RMSEcomparisonofKNNwandKNNMF图8 基于PCA与联合近邻权值的协同过滤算法与基于近邻与矩阵分解混合算法RMSE比较Fig.8 RMSEcomparisonofPCAwithjointlyderivedneighborhoodandKNNMF

图8为本文提出的KNNMF算法与基于PCA与联合近邻权值的协同过滤算法(PCAwKNN)的实验结果对比，PCAwKNN算法是将主成分分析(Principal Component Analysis，PCA)与文献[14]中的近邻插值算法混合，从数据中可知，KNNMF算法的精确度远远高于PCAwKNN算法的精确度.

从三组实验结果的实验数据对比中可知，本算法极大的剔除了与目标用户以及目标项目无关的数据影响，不仅降低了原始评分矩阵的稀疏性影响，而且有效的提高了算法的准确性.

6 总 结

本文提出的K近邻矩阵分解推荐算法，结合了经典矩阵分解算法与最近邻算法的优点.在对未知评分项预测时，同时考虑目标用户与目标项目的最近邻，大大减少了无关用户与项目的相关评分值影响.并提出了新的近邻评分矩阵，对近邻评分矩阵进行矩阵分解，给出了计算未知评分项的新方法.实验结果证明，本文提出的算法对比传统的协同过滤推荐算法得到更准确的推荐结果.

[1] Schafer J B，Konstan J A，Riedl J.E-commerce recommendation applications[J].Data Mining and Knowledge Discovery，2001，5(1)：115-153.

[2] Adomavicius G，ATuzhilin.Towards the next generation of recommend systems：a survey of the state-of-the-art and possible extensions[J].IEEE Transactions on Knowledge and Data Engineering，2005，17(6)：734-749.

[3] KaryPis G.Evaluation of item-based top-n recommendation algorithms[C].Proceedings of the 10th International Conference on Information and Knowledge Management，New York：ACM Press，2001：247-254.

[4] Sarwar B，KaryPis G，Konstan J，et al.Item-based collaborative filtering recommendation algorithms[C].Proceedings of the 10th International Conference on World Wide Web,New York：ACM Press，2001：285-295.

[5] Wu Yan-wen,Wang Jie,Wang Fei.Collaborative filtering recommendation model based on hybrid particle swarm optimization and genetic algorithm[J].Journal of Chinese Computer Systems，2017，38(3)：527-530.

[6] Zhang Feng，Chang Hui-you.Employing BP neural networks to alleviate the sparsity issue in collaborative filtering recommendation algorithms[J].Journal of Computer Research and Development，2006，43(4)：667-672.

[7] Sarwar B M，Karypis G，Konstan J A，et al.Application of dimensionality reduction in recommender system-a case study，TR 00—043 [R].Minneapolis，USA：Department of Computer Science and Engineering，University of Minnesota，2000.

[8] Zhao Liang，Hu Nai-jing，Zhang Shou-zhi.Algorithm design for personalization recommendation systems[J].Journal of Computer Research and Development，2002，39(8)：986-991.

[9] Bell R，Koren Y，Volinsky C.Modeling relationships at multiple scales to improve accuracy of large recommender systems[C].Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining(KDD′07)，2007：95-104.

[10] Koren Y，bell R，Volinsky C.Matrix factorization techniques for recommender systems[J].IEEE Computer Society，2009，42(8)：30-37.

[11] Hu Yi-fan，Yehuda Koren，Chris Volinsky.Collaborative filtering for implicit feedback datasets[C].IEEE International Conference on Data Mining(ICDM′08)，2008：263-272.

[12] Herlocker J L，Konstan J A，Riedl J.An algorithmic framework for performing collaborative filtering[C].Proceedings of the 22nd Annual International ACM SIGIR Conference on Research and Development in Information Retrieval，1999：230-237.

[13] Linden G，Smith B，York J.Amazon.com recommendations：item-to-item collaborative filtering[J].IEEE Internet Computing，2003，7(1)：76-80.

[14] Bell and Koren Y.Scalable collaborative filtering with jointly derived neighborhood interpolation weights[C].IEEE International Conference on Data Mining(ICDM′07)，2007：43-52.

[15] Koren Y.Factorization meets the neighborhood：a multifaceted collaborative filtering model[C].Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD′08)，2008：426-434.

附中文参考文献：

[5] 吴彦文，王 洁，王 飞.混合粒子群遗传算法的协同过滤推荐模型[J].小型微型计算机系统，2017，38(3)：527-530.

[6] 张 锋，常会友.使用BP神经网络缓解协同过滤算法的稀疏性问题[J].计算机研究与发展，2006，43(4)：667-672.

[8] 赵 亮，胡乃静.张守志.个性化推荐算法设计[J].计算机研究与发展，2002，39(8)：986-991.