结合高斯混合模型的关联分类离散化算法研究

吴辰文,郭叔瑾,李晨阳

(兰州交通大学 电子与信息工程学院,兰州 730070) E-mail:2356162345@qq.com

1 引 言

运用规则归纳算法提取的规则可以用于分类,这被称为以规则为基础的分类.在以规则为基础的分类器中使用简单的if-then规则,可以提高分类过程的解释性,并帮助领域专家了解将某一观测值分到某一类别背后的逻辑[1,2].在医疗领域,基于规则的分类器特别重要,它们可以被用于设计临床决策支持系统以提高医疗诊断[3-5].医生可以使用提取的规则来验证分类结果并降低错误分类的可能[6].

虽然它们有优势,但大多数以规则为基础的分类只能处理分类数据,不能直接应用于连续数据[7].然而,大多数数据中包括连续变量,如肿瘤大小,身体质量指数等.因此,需要一个预处理步骤将连续变量转换成离散格式.此预处理步骤被称为离散化,并涉及到使用一组分割点,将连续变量划分为不同的区间.最佳的分类性能,必须选择这样的分割点,即在离散化的数据集上保持原始数据集的模式不变.因此,离散化算法应考虑到多峰分布的连续变量,以保持原始模式.然而,大多数离散化算法的结果并不能反映原来多模态分布的连续变量.它是改变了原来数据的分布且降低了生成规则可靠性的规则归纳算法[8].此外,目前大多数的离散化算法要么集中在最小化间隔数,要么最大化分类准确度.然而,这两个准则都和生成的规则数不直接相关.生成的规则数是基于规则分类器系统的一个重要性能指标,但是目前基于规则分类器的离散化算法忽略了生成规则数目的重要性.

高斯混合模型已被证明是一种有效的工具,用于估计多模态密度的连续变量[9].考虑到这一事实和现有离散化方法的局限性,我们提出了一种有监督离散化算法,称作基于高斯混合模型的离散化算法DAGMM(Discretization Algorithm based on Gaussian Mixture Model).DAGMM算法运用每一个特征的多模态分类密度来确认分割点.运用高斯混合模型捕获多模态密度,高斯分量数由贝叶斯信息准则(Bayesian Information Criterion,BIC)确定.

我们通过DAGMM算法的离散化结果来测试该算法的性能.实验结果表明,已训练的关联分类器的性能在少量规则的生成和高分类精度之间达到了平衡.此外,和6个静态离散化算法的比较表明,DAGMM算法优于其他离散化算法.

2 相关理论

2.1 离散化方法

离散化是将连续特征F映射到m个区间U={[d0,d1],…,[dm-1,dm]}的过程.在本文中,将6个静态离散化算法和DAGMM算法进行比较.这6个算法包括等宽(Equal Width,EW)算法,等频(Equal Frequency,EF)算法,1R算法,类-属性相依系数离散化(Class-Attribute Contingency Coefficient discretization,CACC)算法,基于有效信息比率的离散化算法(EIRDC)和正则化高斯混合模型离散化(Regularized Gaussian Mixture Model discretization,RGMM)算法.在EW算法中,每个区间长度是固定的,而EF算法每个区间的频数是固定的.1R离散化算法对每一个区间和值,都是基于最优分类概念的有监督离散化方法[7].CACC算法使用变量之间的相互依存离散化连续数据[8],EIRDC算法在信息熵的基础上,定义了离散化区间上的有效信息比率[10],RGMM使最优高斯混合模型符合数据集,并根据最大概率准则给每一个高斯混合分量分配一个新样本[11].

2.2 高斯混合模型及其在离散化算法中的应用

高斯混合模型(Gaussian Mixture Model,GMM)是连续型随机变量参数的概率分布,其中密度函数被定义为多个高斯密度加权和[9].在GMM中,高斯函数的离散集合提供更好的建模能力.GMM的数学公式在方程1中被提供[12]

(1)

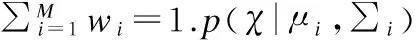
(2)

其中D是χ的维数.

估计GMM的参数最常用的一种方式是最大似然估计(Expectation Maximization,EM)[13].通过优化方程3中定义的对数似然函数的参数,来找到最大似然的迭代方法.

(3)

优化处理包括初始化Θ值(通常是随机的)和迭代更新Θ直到收敛.循环变量j,GMM的参数Θ更新如下:

(4)

(5)

(6)

(7)

运用EM算法从训练集中估计GMM的参数,已成功地应用于各个方面,如在计算视觉中的目标跟踪,在音频处理中说话者的识别和在生物识别技术中的个人身份验证.考虑到高斯混合模型的继承性,将数据分为不同的组,GMM是理想的离散化过程.RGMM适合基于熵和信息损失的最优高斯混合模型,并根据最大概率准则给每一个高斯混合分量分配一个新样本.RGMM是无监督离散化算法,在离散化过程中不考虑类标签.无监督算法的性质限制了它的分类能力,所以进行有监督学习是必要的.因此,为了运用算法RGMM离散化一个新的数据点,对所有已确定高斯分量的新数据点计算其条件概率,并选择高斯分量结果标签中的最大概率值作为新的离散值.这种离散化新值的方法难以解决没有提供用于追踪离散化过程中实际间隔的问题.本文提出的DAGMM算法解决了此限制.

图1 DAGMM算法的5个步骤Fig.1 Five steps of DAGMM algorithm

3 DAGMM算法

3.1 基于高斯混合模型的离散化DAGMM

DAGMM算法包括5个步骤,如图1所示.

步骤1.以类标签C为基础,将数据集分割成不同的子集.

步骤2.运用EM算法,得到符合每一个子集特征的高斯混合模型.这一步需要的两个主要参数包括迭代次数和高斯分量数.迭代次数依经验来定义,高斯分量数由BIC准则来确定的.用一个简单的迭代搜索来识别分量具有最小BIC值的个数.最小BIC准则根据4.3部分的实验测试结果来选择.采用最小BIC有助于避免GMM的过拟合,DAGMM算法平衡了复杂性的降低和信息的损失.

步骤3.在步骤2中使用适当的高斯分量确定每个特征的初始间隔.对于每个高斯分量,定义区间为|μ-3σ,μ+3σ|,其中μ和σ表示相应的高斯分量均值和标准差.初始区间可能包含一些重叠,这些重叠在DAGMM算法接下来的步骤中被移除.

图2 重叠部分的两个处理步骤Fig.2 Two processing steps for overlapping parts

步骤4.使用类比率(Class Ratio,CR)删除初始区间的重叠.CR的定义如下:

(8)

其中Ne是属于类e的观测总量,N是数据集中的观测总量.

阶段1.如果一个区间完全在另一个区间内,并且它们属于同一类,删除位于其它区间有限范围内的区间.如果它们属于不同的类,检查相应的高斯分量的权重,删除属于高斯分量较小的区间(权重×CR)(见图2).

阶段2.运用下列规则删除确定间隔之间剩余的重叠部分:

1)如果两个区间属于同一类.通过设置前区间的上限到处理区间的上限(Upper Limit,UL)来合并两个区间.

2)如果两个区间属于不同的类,检查相应的高斯分量的权重.如果处理区间的(weight×CR)大于前区间的(weight×CR),则前区间的上限UL等于处理区间下限(Lower Limit,LL).如果处理区间的(weight×CR)小于前区间的(weight×CR),则处理区间的下限等于前区间的上限(如图2).删除所有间隔之间的重叠后,给每一个区间分配一个唯一的标识符.

步骤5.运用下列步骤离散化一个新值:

1)如果数据点在任何区间的边界内,则将该区间的标识符作为该数据点的新值.

2)如果数据点在任意区间的边界外,计算所有区间从质心((UL+LL)/2)到数据点的距离,并指定最近的标识符作为数据点的新值.例如,图1中的步骤5中的数据点不属于任何区间.因此,从三个剩余区间的质心计算距离.考虑到距离值(d1>d2>d3),3被分配作为该数据点的新值.

3.2 关联分类

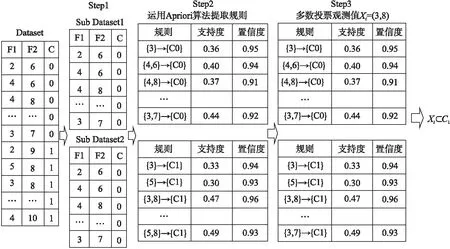
图3 基于简单多数投票的关联分类器Fig.3 Association classifier based on simple majority voting

关联分类是结合关联规则挖掘和分类的一种新的分类方法[14].本文运用一个基于简单多数投票的关联分类器[15]来测试DAGMM算法的性能.简单的关联分类器(如图3)由以下三部分组成:

步骤1.基于每个观测值的类标签,将离散的输入分割成多个子集.对于二进制类标签的数据,分割的结果是两个子数据集.

步骤2.运用Apriori算法从每个子集中提取关联规则.Apriori算法是最受欢迎的关联规则挖掘算法之一,它有两个主要步骤.第一步叫做自连接,满足最小支持度阈值的k-项集需要自连接产生(k+1)-项集[16].第二步叫做剪枝,基于最小支持度准则剪枝(k+1)-项集.使用最小置信度阈值进行过滤,Apriori算法迭代的最终结果项集称为关联规则.

步骤3.一个简单的无加权投票的方法,即多数投票,用于分类一个新的观测值.在投票方案中,一个新的观察值不能测试提取的所有关联规则,把满足规则的多数类标签作为新数据点的类标签.

4 实验及分析

实验平台采用64位的Windows7操作系统,处理器为Intel(R)Core(TM)i5-3210M,内存为4G.实验数据来自UCI机器学习库.实验在MATLAB R2014a平台中实现.

4.1 数据集

在实验中使用四个医疗数据集作为研究对象(如表1 所示).这些数据集包括连续和分类的特征.连续特征归一化到[0,1]范围,把含有缺失值的观测值从数据集中删除.这项研究中数据集中的大多数变量服从非正态分布.

4.2 DAGMM算法性能评价

使用在第三部分引入的关联分类来评价DAGMM离散化算法的性能.关联分类的最小支持度和最小置信度分别设置为0.3和0.9.设置高支持度和置信度阈值,以确保从数据集的频繁模式中提取规则,而不是由罕见的模式所造成的异常提取.在医疗领域设置高支持度和置信度是特别重要的,因为想提取可靠的规则,更广泛地应用于患者.提取具有高支持度和置信度的规则,需要在连续数据集中保持原始模式,是一个很好的评价离散化算法的指标.

运用5折交叉验证评价关联分类性能.在5折交叉验证方法中,数据集被等分成5组.接下来,4组用于训练集,剩下的1组作为测试集.此过程被重复5次直到每组都被选作为测试集.整体性能,即分类准确度和规则数目,计算5次迭代过程中所有记录性能的平均值作为整体性能.一种排序方法用于简化结果的比较.排序工作是通过分配从一到最佳性能(最大分类准确度或最少规则数)的排序,并逐步增加排名,直到达到最坏的性能.N/A表示关联分类情况下没有产生任何结果,最后给出了最大排名.整体的排名是计算分类准确度平均排名的数目和产生规则的数目.应当指出的是,区间数量只供参考,并没有用于整体排名的计算.原因是,我们的研究结果和以前的研究结果表明,确定的区间数目和分类性能之间没有直接的关系.

表1 UCI中的四个医疗数据集
Table 1 Four medical data sets in UCI

数据集样本数(正/负)特征数连续特征数帕金森氏症195(48/147)2222乳腺癌569(357/212)3030糖尿病768(268/500)82肝脏病583(167/461)105

4.3 敏感性分析

DAGMM算法的一个关键参数是高斯分量数.选择大量的高斯分量可能导致过拟合,而少量的高斯分量可能不足以捕捉到数据的多模态密度.可以使用统计选择模型选择高斯分量的数目.两大统计选择模型包括赤池信息准则(Akaike Information Criterion,AIC)和BIC.AIC和BIC通过引入一个惩罚项来平衡复杂性和模型的拟合优度[17].

表2 五折交叉验证的结果
Table 2 Result of 5-CV

模型选择标准数据集帕金森氏症乳腺癌糖尿病肝脏病平均排名总体排名分类准确度min(AIC+BIC)/279.7561.12N/A57.503.438.25min(AIC)N/A64.98N/AN/A6.6113.08min(BIC)84.1168.1673.1262.081.496.26min(AIC*BIC)N/A61.8250.0351.857.0111.51min(AIC+BIC+(AIC*BIC))N/A60.7750.0351.857.1811.51产生规则的平均值min(AIC+BIC)/231.8877.62N/A21.824.84min(AIC)N/A59.02N/AN/A6.51min(BIC)33.2189.8813.0222.614.84min(AIC*BIC)N/A16.6217.0116.454.33min(AIC+BIC+(AIC*BIC))N/A17.2517.0116.454.50区间总数min(AIC+BIC)/2152205N/A804.33min(AIC)N/A263N/AN/A7.35min(BIC)13717859601.16min(AIC*BIC)N/A78051907.00min(AIC+BIC+(AIC*BIC))N/A76751906.82

因此,我们为确定最佳模型选择标准进行了敏感性分析,即在DAGMM算法中确定高斯分量的数量.每个候选标准被用来确定在DAGMM算法中分量的数量.接下来,关联分类被应用到离散化的数据集.表2提供了运用5折交叉验证方法产生的详细结果.根据整体排名,min(BIC)提供最好的结果,因此被用来在DAGMM算法中确定高斯分量数.其中,N/A表示在支持度和置信度分别设置为0.3和0.9时关联分类器无法提取任何规则.

4.4 DAGMM算法的性能

把六个静态离散化算法与DAGMM算法进行比较.离散化算法的参数根据经验或根据现有的文献进行设置.将1R算法的每个区间数据点的最小数目设置为6.EW算法储存数量和EF算法每一个箱中储存的数据点设置为5.最后,用30个分量的最大值设置迭代45000次,得到DAGMM算法和RGMM算法的EM参数.图4和表3展示了把关联分类应用于离散化数据集得到的详细结果.

从图4可以看出,DAGMM算法在生成较少的规则时,就可以达到较高的分类准确度.同一种疾病中的空白间隔代表未生成规则.根据总体排名,和其他静态离散化算法相比,DAGMM算法产生了更好的结果.此外,只有四个离散化算法(DAGMM,1R,EW,EIRDC)能够以高支持度和置信度在测试集上提取规则.以高支持度和置信度值提取规则意味着这四种算法都能保持原始连续数据集的最频繁模式,而其它两种方法(CACC,EF)是无法保持此模式的.

图4 DAGMM算法和六个静态离散化算法在四个数据集上执行结果的比较Fig.4 Comparison of the results of the DAGMM algorithm and six static discretization algorithms on four datasets

表3 离散化数据集得到的详细结果
Table 3 Results obtained by a discreting datasets

离散化方法分类准确度平均排名产生规则的平均值平均排名区间总数平均排名总体排名DAGMM1.162.493.003.65RGMM4.674.672.679.33EF5.515.165.5010.671R3.331.504.174.83EIRDC3.084.764.197.52CACC3.174.604.337.67EW4.003.502.167.50

实验结果表明,所测试数据集的基本分布不影响DAGMM算法的性能,而它对其他测试离散化算法的性能有显著影响.特别是,EIRDC 算法和CACC算法的性能相差不大,但CACC算法在含有很多异常值的数据集中不能很好地执行.通过运用关联分类器产生大量的规则来看,1R算法执行的很好.然而,对不平衡数据集的分类准确度不好.在EF算法中,两种观测得到的同一个值可能被分到不同的区间,这会导致数据集的原始分布发生相当大的改变.初始分布的变化改变了连续数据集的模式和,并使关联分类器的性能变差.RGMM算法适合基于熵和信息损失的最优高斯混合模型,并根据最大概率准则分配给每一个高斯混合分量一个新的样本.RGMM算法利用信息理论拟合最优高斯混合模型,而DAGMM算法使用BIC准则确定最优的高斯混合模型.RGMM算法和DAGMM算法之间的另一个主要区别是,RGMM是无监督离散化方法而DAGMM是有监督的离散化方法.根据等式(1-7),用∑i|C代替∑i,其中C指类标签.因此,DAGMM算法考虑在离散化过程中的类标签信息.然而,运用∑i|C也意味着每一个变量必须符合C高斯混合模型,这就增加了DAGMM算法的计算时间.最后,RGMM和DAGMM之间的其他区别是新数据点的离散方式不同.更具体地说,RGMM算法的新数据点xt被分配到高斯分量Gi,其满足arg maxip(xt|Gi).而在DAGMM算法中,新数据点被分配到最近的间隔arg minint‖χt-γint‖,在每个区间(int)对应[μ-3σ,μ+3σ]适合于高斯混合模型分量,γ代表每个区间的中点值.因此,DAGMM算法比RGMM算法更容易理解.

5 结 论

离散化是现代专家系统设计不可分割的一部分,也是从大量的数据中提取逻辑规则必不可少的.可在临床专家系统中运用DAGMM算法,有潜力提高以规则为基础的分类器的性能.DAGMM算法的潜在应用是设计临床决策支持系统,为医生提供可解释的结果.本文提出的DAGMM算法,它考虑了原始连续变量的多模态分类密度.DAGMM算法使用统计模型选择准则平衡离散化过程中的信息损失和复杂性的降低,从而转化为更高的分类精度,和更低的以规则为基础分类的规则数目.高斯混合模型的局限性之一是确定高斯分量的最佳数量.在本文中,使用了一个启发式方法,适合不同数量分量的高斯混合模型,并根据BIC准则选择最好的分量数目.然而,这种方法的计算是耗时的,我们仍然需要为高斯分量的最大数量提供一个上限.假设最佳分量数是已知的,使用EM算法拟合高斯混合模型的计算仍然是耗时的.因此,需要进一步分析确定DAGMM算法的复杂性和提高计算效率.最后,DAGMM算法没有考虑到在离散化过程中变量之间的相互关系,而是考虑了数据集中独立变量之间的相互关系,可以提高离散化算法的性能,并在离散化过程中提供新的见解.针对DAGMM算法的不足,需在未来对其复杂度和计算时间方面进一步进行研究.

[1] Kononenko I.Machine learning for medical diagnosis:history,state of the art and perspective[J].Artificial Intelligence in Medicine,2001,23(1):89-109.

[2] Zhou Zhi-hua,Jiang Yuan.Medical diagnosis with C4.5 Rule preceded by artificial neural network ensemble[J].Information Technology in Biomedicine,IEEE Transactions on,2003,7(1):37-42.

[3] Nura Esfandiari,Mohammad Reza Babavalian,Amir-Masoud Eftekhari Moghadam,et al.Knowledge discovery in medicine:current issue and future trend[J].Expert Systems with Applications,2014,41(9):4434-4463.

[4] Peter B Jensen,Lars J Jensen,Søren Brunak.Mining electronic health records:towards better research applications and clinical care[J].Nature Reviews Genetics,2012,13(6):395-405.

[5] Maslove,David M,Podchiyska,et al.Discretization of continuous features in clinical datasets[J].Journal of the American Medical Informatics Association,2013,20(3):544-553.

[6] Paul R,Harper.A review and comparison of classification algorithms for medical decision making[J].Health Policy,2005,71(3):315-331.

[7] Huan Liu,Farhad Hussain,Chew Lim Tan,et al.Discretization:an enabling technique[J].Data Mining and Knowledge Discovery,2002,6(4):393-423.

[8] Cheng-Jung Tsaia,Chien-I.Leeb,Wei-Pang Yangc.A discretization algorithm based on class-attribute contingency coefficient[J].Information Sciences,2008,178(3):714-731.[9] Reynolds D.Gaussian mixture models[J].Encyclopedia of Biometrics,2009,3(4):93-105.

[10] Zhu Wen-zhi,Wang Jing-cheng,Zhang Yan-bin,et al.Discretization algorithm based on effective information ratio[J].Xi′an Jiaotong University Xuebao,2011,45(4):12-18.

[11] Cai Rui-chu,Hao Zhi-feng,et al.Regularized gaussian mixture model based discretization for gene expression data association mining[J].Applied Intelligence,2013,39(3):607-613.

[12] Xu Lei,Jordan.On convergence properties of the EM algorithm for gaussian mixtures[J].Neural Computation,1996,8(1):129-151.

[13] Qiao Shao-jie,Jin Kun,Han Nan,et al.Trajectory prediction algorithm based on gaussian mixture model[J].Journal of Software,2015,26(5):1048-1063.

[14] Sun Yan-min,Andrew K C Wong,Yang Wang.An overview of associative classifiers[C].International Conference on Data Mining,2006.

[15] Pan Xiao-chuan,Sidky,et al.Advanced signal processing handbook:theory and implementation for radar,sonar,and medical imaging real-time systems[J].Medical Physics,2003,30(5):234-240.

[16] Wang Wei-ping,Zhou Zhong-mei,Zheng Yi-feng,An improved associative classification approach based on support and enhancement ratio[J].Computer Engineering&Science,2016,30(2):370-375.

[17] Byram G M,Nelson,et al.Multimodel inference:understanding AIC and BIC in model selection[J].International Journal of Wildland Fire,2012,21(2):261-304.

附中文参考文献：

[10] 诸文智,王靖程,张彦斌,等.应用有效信息比率的离散化算法[J].西安交通大学学报,2011,45(4):12-18.

[13] 乔少杰,金 琨,韩 楠,等.一种基于高斯混合模型的轨迹预测算法[J].软件学报,2015,26(5):1048-1063.

[16] 王卫平,周忠眉,郑艺峰.基于支持度和增比率的改进关联分类算法[J].计算机工程与科学,2016,30(2):370-375.