一种简单的基于事件触发的时间同步算法

唐 波,孙 超,彭 力

(江南大学 物联网工程学院,江苏 无锡 214122) E-mail:tangb1992@foxmail.com

1 引 言

无线传感器网络节点具有廉价、能量有限和无线通信等特点,节点的信息交互、数据分析都与时间顺序信息密切相关,涉及到的应用包括定位、休眠以及数据融合等,因此时间同步技术是无线传感器网络中的一项基础支撑技术[1].随着研究的深入,提出的算法从集中式[2]的算法如RBS(Reference-Broadcast Synchronization)算法和TPSN算法(Timing-sync Protocol for Sensor Networks)演变到分布式[3]的GCS(Global Clock Synchronization)算法、ATS(Average TimeSync)算法以及Gossip算法,近年来时间同步的研究热点从提高同步算法的精度延伸的同步服务的性能方面.

分布式时间同步算法强调参考节点无关性,每个节点利用与周围邻居节点的消息交换,进而实现全网的时间同步.在分布式算法中,迭代轮次的控制通常根据设定好的时间间隔依次执行,虽然传感器节点的时钟频率不一致,但是执行同步过程是有序执行的,这样保证能实现一致性.在上述分布式同步的过程中,每个节点按照一定的时间间隔询问周围节点的时间信息并更新自身的时间,这样的过程重复若干次之后全网节点的时间达到同步.分布式时间同步算法有效地提高了算法的可扩展性和鲁棒性,但是明显会带来通信量的增加,并且随着精度要求越高、网络规模越来越大,能耗会显著增加.

事件的概念由来已久,最早在控制系统中事件指代实际的输入、输出和期望的输入、输出的不同.文献[4]提出的事件触发控制系统中控制输入只在状态量超过某个阈值的时候加入,基于这样的设计使得控制器具有更少的状态变化.文献[5]提出了一种能有效减少反馈通信的事件触发控制器,事件触发器负责状态值的采样更新,使得系统能够有效的节省资源尤其是通讯资源.基于分布式算法的现状和事件触发的应用,事件触发方式的时间同步算法被提了出来,这种算法执行同步先后顺序不依赖各个节点的时钟快慢和同步间隔,而是依赖于指定的事件,进一步的说依赖于阈值,各个节点在阈值被满足时触发自身时间同步过程,通过这种方式可以有效的降低时间同步算法执行的次数即通信量的降低.文献[6]提出的事件驱动时间同步算法在分布式算法的基础上,针对虚拟时钟模型的漂移量补偿更新和偏移量补偿更新加上事件驱动模型,有效的降低了同步算法同步消息交换的次数,并且实现了虚拟时钟的同步.文献[7]提出的算法将时间同步过程看成二阶状态模型并设计了事件触发函数,通过理论和仿真实验证明了算法的有效性.

本文研究了基于事件触发的时间同步算法,针对绝对时间的更新加上事件触发策略,同时对事件触发函数的设计做了改进,提出了一种简单的基于事件触发的时间同步算法,通过理论和仿真实验证明了算法的有效性和优势.

2 事件触发基础知识

为了更好的理解事件触发机制,本节主要介绍在多智能体领域内事件触发机制的应用作为基础知识.

针对一阶多智能体系统,智能体i的动态方程如下

(1)

其中xi(t)表示智能体i的状态,ui(t)表示智能体i的控制输入.考虑如下简单的控制输入

(2)

类似于Tabuadad[8]的思想,对每个多智能体引入一个状态测量误差ei(t),那么整个系统的状态测量误差向量为e(t)=(e1(t),e2(t),…,en(t))T,事件触发的具体时间由下式(3)决定.

f(e(t))=0

(3)

根据事件触发函数可以得到一系列时间触发时刻{tk},k=0,1,…,在每个触发时刻均有f(e(tk))=0,k=0,1,…,对应的控制输入为u(t0),u(t1),….当事件触发时更新控制输入,两个触发事件中间的控制输入不变,满足下式(4).

u(t)=u(tk)t∈[tk,tk+1),k=0,1,…

(4)

系统状态测量误差具体的定义如下

e(t)=x(tk)-x(t)t∈[tk,tk+1),k=0,1,…

(5)

再由式(2)可知,实际的事件触发下的控制输入如下

(6)

其向量形式为

u(t)=-Lx(tk)t∈[tk,tk+1)

(7)

其中L表示网络拓扑的拉普拉斯矩阵,那么系统的闭环形式如下

(8)

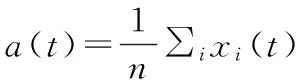
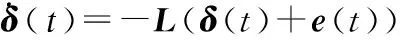
(9)

对式(9)选取李雅普诺夫函数证明稳定性,并由此推导得到满足系统稳定性的事件触发函数.证明推导过程见文献[10],求得的触发函数如下

(10)

其中λ2(L)表示图对应的拉普拉斯阵的第二小特征值.从式(10)我们看出事件触发函数中需要知晓图拉普拉斯阵的特征值和分歧向量,所以这种触发方式也被称为集中式事件触发方式.

3 事件触发在时间同步中的应用

由第2节关于事件驱动机制的介绍我们了解了事件触发的控制输入、测量误差和触发函数等基本知识.在多智能体系统中基于连续时间系统的事件触发算法[5]与时间同步迭代算法离散时间模型不符合,因为对于时间同步算法而言理想时间是未知的,也不能直接使用.文献[11]的多智能体事件触发虽然是基于离散时间模型,但是触发函数是集中式的对于分布式时间同步算法而言不适用.文献[12]提出的多智能体采样事件触发算法有适用时间同步算法的触发函数,但是采样的假设前提是多智能体具有相同的时间系统.综上所述虽然事件触发算法应用广泛,但是对于时间同步而言适用性不强.

文献[6]最早提出了基于事件触发的时间同步算法,文献[7]提出了基于二阶状态模型的时间同步算法.本章提出的算法在这两篇文献的基础上,受文献[5]提出的触发函数启发,提出了一种针对绝对时间的基于事件触发的时间同步算法,算法折中了时变触发函数和固定阈值触发函数,有效的避免了固定阈值触发函数前期频繁触发和时变触发函数后期频繁触发的负面影响.

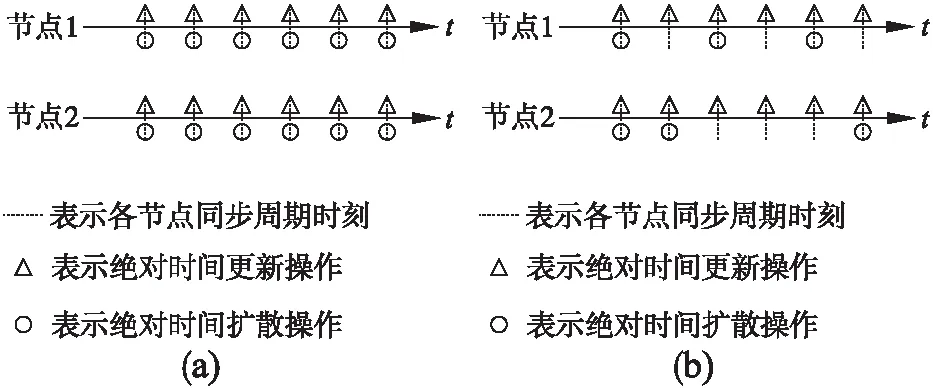
图1 分布式和事件触发式时间同步示意图Fig.1 Distributed and event triggering time synchronization diagram

类似文献[6]的事件触发策略,本章提出事件触发机制如图1(b)所示,图1(a)表示一致性时间同步示意图,按照各个节点的同步周期进行绝对时间的更新和扩散操作,图1(b)表示本章的事件触发事件同步示意图,在各个节点的第一个同步周期进行绝对时间的更新和扩散操作,在接下来的时间里按照同步周期进行绝对时间的更新操作,按照事件触发函数进行绝对时间的扩散操作.这里指的扩散和广播、消息交换指的同一个概念.为了更好的说明同步算法,假设本地时钟的更新对绝对时间没有影响,也就是说在整个时间同步算法执行开始到实现时间同步,绝对时间不是连续的.

3.1 绝对时间更新模型及事件触发函数设计

对节点i,假设节点的绝对时间更新时刻为k,k=1,2,…,事件触发的绝对时间扩散时刻为kl,l=1,2,…,kl集合是k集合的子集,每个节点的第一次更新时刻和触发时刻重合.设节点i的绝对时间为τi,类似文献[11]的状态更新模型,绝对时间更新如下：

(11)

其中ε∈(0,1/Δ)为统一权重常数,Δ为节点的最大度.记测量误差ei(k)=τi(kl)-τi(k),绝对时间扩散的事件触发函数如下：

fi(ei(k))=δk+ξ=0,δ∈(0,1)

(12)

其中δ表示0到1之间的常数;ξ表示与绝对时间同步精度相关的常数,数量级为同步精度要求的数量级.

记τ(k)=(τ1(k),…,τn(k))T,τ(kl)=(τ1(kl),…,τn(kl))T,e(k)=(e1(k),…en(k)),那么式(11)可写成如下形式：

τ(k+1)=τ(k)-εLτ(kl)=τ(k)-εL(e(k)+τ(k))=

(I-εL)τ(k)-εLe(k)

(13)

类似文献[9]将式(13)中的I-εL看成具有ε参数的培龙矩阵P,经过M次更新之后绝对时间表达式如下：

(14)

与文献[6]证明过程类似,需要用到的定义和引理如下：

定义1[13].对于随机矩阵F∈n×n,矩阵的遍历性系数(Coefficient of Ergodicity)为

引理1[13].对向量υ∈n,S(υ)定义为向量υ中元素的最大差值,S(υ)=maxi,j|υi-υj|,且S(υ)具有如下加性和乘性的性质

1.对向量υ和ω,S(υ+ω)≤S(υ)+S(ω)

2.对随机矩阵F和向量υ,S(Fυ)≤γ(F)S(υ)

证明过程如下,对式(14)求取向量元素的最大差值得到

(15)

其中S(PMτ(0))部分,根据培龙矩阵P的性质和文献[9]的证明可知,S(PMτ(0))=0,M→∞.再根据S(εLe(q))≤2ε‖Le(q)‖∞≤4εΔ‖e(q)‖∞,结合公式(12)事件触发函数得到S(εLe(q))≤4εΔ(δq+ξ),当q→∞时,S(εLe(q))→4εΔξ.根据这两部分,式(15)的极限进一步放缩如下

(16)

根据文献[6]可知γ(P)∈(0,1),那么

(17)

3.2 仿真实验

使用Matlab进行仿真实验,传感器节点的拓扑结构为环形拓扑结构,节点的数量为8个,如图2所示.

如图3(a)所示时间触发下的绝对时间值随着更新次数的增加趋于一致;图3(b)展示了各个节点广播自身绝对时间值的时刻,从图中可以看出广播时刻密集,引起大量的通信消耗.

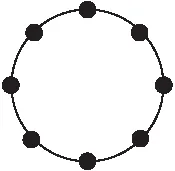
图2 8节点环形拓扑示意图Fig.2 8-node ring topology diagram

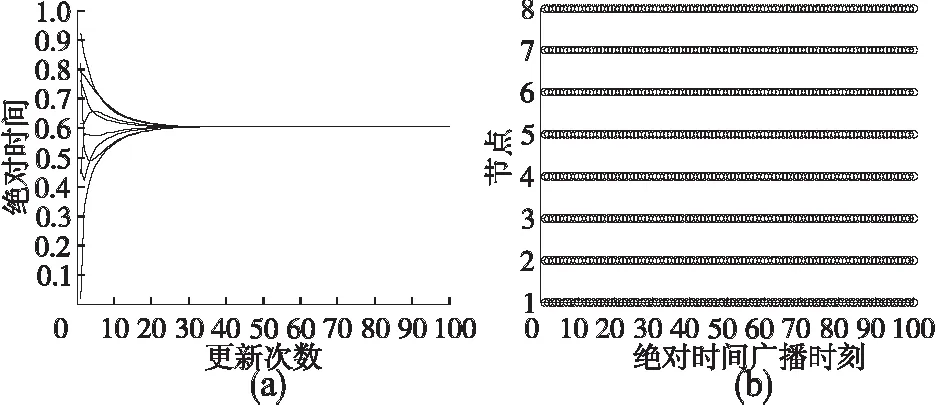
图3 时间触发下绝对时间状态图和节点的广播时刻图Fig.3 Absolute time state and the node′s broadcast time diagram under time triggerring

相比于图3(a),图4(a)在更新次数靠前的时刻存在较大震荡,但是绝对时间也是收敛的.时间触发方式在第68次更新时达到同步精度要求,事件触发方式在第67次更新时达到同步精度要求.对比图3(b)和图4(b)可知,以事件触发方式广播绝对时间实现同步的方式具有更少的广播时刻,也就意味着是节省能量的.说明了针对绝对时间以指数函数和固定阈值的和作为触发函数的时间同步算法的可行性和节省能量的优势.

图4 事件触发下绝对时间状态图和节点的广播时刻图Fig.4 Absolute time state and the node′s broadcast time diagram under event triggerring

将文献[6]提出的时变阈值算法触发函数和固定阈值触发函数用本文的简化模型做对比,如图5(a)和图5(b)所示.对比图4(b)和图5(a)、图5(b)可见,本章提出的触发函数取得了折中的效果,避免了前期频繁触发和后期频繁触发的负面影响,在绝对时间广播时刻上分布更加均匀,相比两者来说取得了更少的广播次数,为时间同步算法节省了能量消耗.

4 结束语

本文研究了一种基于事件触发的时间同步算法.为了减少分布式时间同步算法在迭代过程中大量通信广播带来的能量消耗,将事件的概念引入时间同步算法中.提出的算法利用事件触发的方式取代时间间隔触发同步消息广播的方式,改进了触发函数,在保证分布式同步算法的收敛性的同时避免了同步消息广播的频繁触发,降低了同步算法通信能量消耗.

图5 时变阈值算法和固定阈值算法绝对时间广播时刻示意图Fig.5 Node′s broadcast time diagram under time varying threshold and fixed threshold

[1] Swain A R,Hansdah R C.A model for the classification and survey of clock synchronization protocols in WSNs[J].Ad Hoc Networks,2015,27(C):219-241.

[2] Benzaïd C,Bagaa M,Younis M.Efficient clock synchronization for clustered wireless sensor networks[J].Ad Hoc Networks,2016,56(C):13-27.

[3] Luo B,Cheng L,Wu Y C.Fully distributed clock synchronization in wireless sensor networks under exponential delays[J].Signal Processing,2016,125(C):261-273.

[4] Astrom K J,Bernhardsson B M.Comparison of riemann and lebesgue sampling for first order stochastic systems[C].The 41st IEEE Conference on Decision and Control,2002:2011-2016.

[5] Seyboth G,Dimarogonas D V,Johansson K H.Control of multi-agent systems via event-based communication[C].Proc.Ifac World Congress,2011:10086-10091.

[6] Kadowaki Y,Ishii H.Event-based distributed clock synchronization for wireless sensor networks[C].IEEE Conference on Decision and Control,2013:6747-6752.

[7] Chen Z,Li D,Huang Y,et al.Event-triggered communication for distributed time synchronization in WSNs[C].Chinese Control Conference,2015:7789-7794.

[8] Tabuada P.Event-triggered real-time scheduling of stabilizing control tasks[J].IEEE Transactions on Automatic Control,2007,52(9):1680-1685.

[9] Olfati-Saber R,Murray R M.Consensus problems in networks of agents with switching topology and time-delays[J].IEEE Transactions on Automatic Control,2004,49(9):1520-1533.

[10] Zhou Y,Hu J.Event-based bipartite consensus on signed networks[C].IEEE International Conference on Cyber Technology in Automation Control and Intelligent Systems,2013:326-330.

[11] Chen X,Hao F.Event-triggered average consensus control for discrete-time multi-agent systems[J].Iet Control Theory & Applications,2012,6(16):2493-2498.

[12] Cao J,Wu Z,Peng L.Distributed event-triggered average consensus of multi-agent systems[J].International Journal of Computer Science,2015,10(3):5-11.

[13] Hartfiel D J.Markov set-chains[M].Heidelberg:Springer,1998.