结合分区和改进ICP的三维颅骨自动配准算法

史重阳,刘晓宁,罗星海,胡晓静,耿国华

(西北大学 信息科学与技术学院,西安 710127) E-mail:xnliu@nwu.edu.cn

1 引 言

颅面复原是对未知颅骨根据统计先验知识恢复其生前面貌的一种技术[1].为此需要建立科学、有效的参考颅骨与所有样本颅骨形状关系的统计计算模型,即颅骨形态学统计.为了对颅骨形态进行统计分析,在建立颅骨数据库时,需要对所有样本颅骨点云数据与参考颅骨进行配准,将它们统一到一个坐标系下,从而对颅骨形态进一步分析.此外,面对一个未知颅骨,基于配准的颅骨复原方法也需要从颅骨数据库中检索出最相似的颅骨.因此,颅骨配准是颅面复原的一个关键步骤.

由于获取的颅骨是三维的,因此三维颅骨配准属于三维模型配准的具体应用.目前,常用的三维配准算法是由Besl等提出的迭代最近点(Iterated Closest Point,ICP)算法,该方法本质是基于最小二乘法的最优配准方法,运用Euclidean距离计算得到与特征点最近的匹配点,估算最优的变换矩阵参数,直到满足正确配准的收敛精度要求[2].但是该算法对初始位置和匹配点对的要求比较高,容易形成局部迭代收敛,造成迭代收敛速度低.为此,国内外学者对此算法进行了改进.文献[3]提出了一种基于点到平面的改进ICP算法,改进了ICP算法中点对点欧氏距离的评价函数.文献[4]提出了对点云对应点赋予权重,剔除权重大于阈值的匹配点对,通过对目标函数引入M-估计(M-estimation),剔除异常点,有效的确定了初始位置和匹配点对.liu等提出了基于遗传(Genetic Algorithm,GA)算法和ICP的配准算法[5],GA是一种全局的搜索算法,很好的解决了ICP容易形成局部迭代的问题,但是GA算法时间复杂度较大.KO等提出基于曲面几何特征性质的配准算法[6],与迭代配准算法相比,该算法的配准时耗明显降低.文献[7]提出采用几何哈希方法找出使得最多数量的点对法矢一致的变换,运用该变换对散乱点云作初始配准,再运用ICP算法进行精确配准.文献[8]提出了一种基于曲率特征的配准算法,该方法根据曲率相似度约束进行配准.文献[9,10]提出一种基于有界旋转角的配准算法,该方法在ICP算法的基础上通过设置旋转角度的边界来改进算法,从而提高了配准的准确度.

也有很多学者对三维颅骨配准进行了研究.Du等提出了一种基于ICP和薄板样条函数(Thin-plate Spline,TPS)的三维颅骨配准算法[11],该方法引入积分不变量的多尺度约束,选定最佳匹配点,然后采用ICP实现初始配准,利用TPS实现精确配准.该方法提高了配准的准确度,但是ICP和TPS都是迭代算法,因此增加了配准的时间复杂度.He等提出了以TPS算法实现颅骨的初始配准,然后根据欧氏距离与局部几何特征的加权距离实现颅骨的精确配准的自动配准算法[12].M.Berar等提出了一种新的3D网格弹性配准方法[13],该方法是基于多分辨率,对定义顶点的两个网格实现对称距离最小化.该方法有效的提高了配准的准确度,但是对于多顶点的网格模型,实现对称距离最小化,使得计算量过大,从而增加了配准的时耗.Yusuf Sahillioglu等提出了一种基于三维立体形状体积的配准算法[14],该方法根据颅骨四面体网格模型,获取数据的体积性质进行配准.与网格模型相比,能更好的捕获数据的体积性质,利用体积性质进行配准,对于畸形的颅骨具有一定的鲁棒性.但是该方法在网格划分的过程中,会丢失一些数据,从而降低配准的准确度.

综上所述,目前颅骨配准具有配准效率不高,配准准确度低,对缺损或者畸形颅骨没有一定的鲁棒性等问题.本文针对配准效率和准确度不高等问题,提出一种在区域划分的基础上,引入动态估计(Destimation)的ICP配准算法.该算法避免的点云数据量过大而导致的计算量过大的问题,为精确配准阶段提供了良好的初始值,根据引入的Destimation有效剔除了误匹配点对,降低了匹配点对的数量,有效提高了配准的准确度以及效率,使得迭代收敛性更快.

2 RANSAC算法

随机抽样一致(Random Sample Consensus,RANSAC)算法思想是从一组包含局外点的观测数据集中,通过迭代的方法计算出数据的数学模型参数,产生最大一致性数据集.该算法的基本假设是样本中包含正确数据(inliers,可以被模型描述的数据),也包含异常数据(outliers,偏离正常范围很远,无法自适应数学模型的数据),即数据集中含有噪声.这些异常数据产生的原因是错误的测量、假设或计算等.本文数据集中的异常数据是在初始配准中寻找匹配点对时产生的误匹配点对.该算法通过反复选择样本数据中的一组随机子集来达成目标[15].

RANSAC基本思想描述如下:

1)存在一个最小抽样集,其个数为n(n为初始化模型参数所需的最小样本数)和一个样本集N,其中|N|>n,从N中随机抽取n个样本,构成N的子集S,用来初始化模型W.

2)余集SC=NS中与模型W的误差小于某一设定阈值ε的样本集合和集合S构成集合S′.S′是内点集,它们构成S的一致集.

3)若内点集的个数大于样本集N的个数,则得到正确的模型参数,并根据内点集S′,采用最小二乘等方法重新设计新的模型W′.重新随机抽取新的样本子集S,否则返回步骤1)进行迭代.

4)在完成一定的抽样次数后,若未找到一致集,则算法失败,否则选取抽样后得到的最大一致集判断内外点,算法结束.

3 颅骨区域划分

根据基于Euclidean距离的Voronoi图对待匹配点集P和参考点集Q进行区域划分.首先对颅骨数据进行随机均匀采样,得到采样点集{v1,v2,v3,…,vn}和{u1,u2,u3,…,um}.然后以采样点为初始聚类点,得到每个采样点的划分区域.如公式(1)所示:

(1)

其中,vi属于P,uj属于Q;n表示待匹配点集P得到的采样点集元素的个数,即P的区域数目;m表示参考点集Q得到的采样点集元素的个数,即Q的区域数目.区域的数目由颅骨的五官和点云数目决定,在实际应用中通常设置为1～9.当颅骨点云数目比较多时,区域数目需要设置大一些.当区域数目取1时,算法退化为全局配准算法.

4 颅骨自动配准算法

经典ICP算法对两个输入颅骨数据的初始相对位置要求较高,若两个数据相对位置较大则易陷入局部最优,得到错误的配准结果.算法时间复杂度较大,为O(NpNq),其中Np和Nq分别是待匹配点集和参考点集的点云个数.该算法中使用Euclidean距离作为唯一约束,约束条件单一,配准准确度不高.

本文提出的算法在初始配准中,运用区域划分思想,有效缩小配准规模,极大缓解了时间复杂度大的问题,为精确配准阶段提供了有效的初始值,本文借助的RANSAC算法,对噪声具有较高的鲁棒性,提高了配准的准确度[16].在精确配准中,采用kd树(kd-tree)算法加快搜索速度,引入Destimation来剔除误匹配点对,有效提高了配准的准确度,降低了配准的时耗.

4.1 初始配准

4.1.1 区域配准

两个区域的配准是两个更小规模的点云数据的配准.首先计算区域Vk和区域Ut的质心,如公式(2)所示:

(2)

然后,根据Euclidean距离相似度和K近邻(k-Nearest Neighbor,KNN)算法,对每一个区域Vk,在待匹配区域Ut中搜索与Vk的质心之间Euclidean距离最近的K个相似区域Ua(a=1,2,3,…,K),如公式(3)所示:

‖o(pk)-o(qt)‖≤ξ1

(3)

其中,ξ1为大于0的实数.

(4)

(5)

其中,ξ2为大于0的实数.

(6)

图1(a)、(b)中左图为颅骨扫描数据集中待匹配点集的鼻子和下颚区域,图1(a)、(b)中右图表示鼻子和下颚区域与参考点集相似区域的配准结果,区域配准的匹配程度对应φ的取值.可以看出,对于2个部分重叠区域进行配准能够有效的得到精确的配准结果.

4.1.2 求解全局刚体变换

(7)

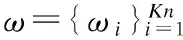
(8)

图1 区域配准结果示意图Fig.1 Result of Region registration

E(ω)=ωTAω
‖ω‖2=1,ω≥0

(9)

为了得到全局刚体变换矩阵T,首先假设将T分解为一个旋转矩阵R和一个平移矩阵t,然后将线性变换矩阵T′分解为一个旋转矩阵R′和平移矩阵t′.令t=t′,根据四元素法求得旋转矩阵R.最后,用T对P和Q完成初始配准.

4.2 引入动态估计的ICP算法

在点云数据配准的研究中,经典ICP算法是最基础、最广泛使用的配准算法[19,20].该算法针对点集中的每个点,在目标点集中全局搜索与其Euclidean距离最近的匹配点,然后估计变换矩阵参数,反复迭代,直到迭代的目标函数值小于等于预设的阈值为止.

在经典ICP算法中,利用Euclidean距离计算每个点的最近点,容易出现误匹配点对,并且匹配点对数量大,这是配准准确度低和配准时耗高的瓶颈所在.如果提前删除误配的匹配点对,在迭代过程中将显著的减少算法的计算量,有效提高配准的准确度,降低了配准的时间复杂度.

在统计学中,均差和标准差是判定样本的有效性和无偏性的标准,因此本文提出Destimation思想,匹配点对之间距离在一定范围内与均差越近似,正确率就越大,由此标准来有效剔除误配或错配的匹配点对.计算均差μd和标准差δd如公式(10)所示:

(10)

其中,di表示匹配点对之间的距离‖pi-qj‖,Np表示根据kd-tree算法求得的匹配点对数.

根据(10)式计算Destimation,如公式(11)所示:

(11)

其中,λ为动态参数,为大于0的实数.

根据(11)对每个匹配点对设置一个动态估计Destimation.根据给定阈值ξ3,如果匹配点对的Destimation<ξ3,则删除该匹配点对,ξ3为大于0的实数.

本文采用均方根误差RMSE作为配准误差[21].此度量方法直观、严谨,有效的弥补了经典ICP误差函数的缺陷.如公式(12)所示:

(12)

其中Np表示待匹配点集P的元素个数,即匹配点对数.pi为待匹配点集P中的点,qj为参考点集Q中与pi相匹配的匹配点.

4.3 三维颅骨配准算法

本文将颅骨配准算法分两阶段进行:

1)初始配准.给定待匹配点集P和参考点集Q,初始配准步骤如下:

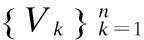
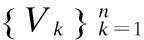
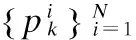
Step5.根据E(ω)求得最优变换矩阵的线性组合T′,易得平移矩阵t,由四素法求得旋转矩阵R,继而得到刚性变换矩阵T,完成初始配准.

2)精确配准.输入初始配准的结果,初始化迭代次数η=0.步骤如下:

Step2.由公式(11)得到Destimation,删除Dη(i)中Destimation<ξ3的匹配点对.

Step3.根据四元素法计算得到旋转矩阵R和平移向量T.

Step4.根据R,T更新Dη(i),即Pη+1=RηPη+Tη,Dη+1(i)=qj,由公式(12)得到误差函数RMSEη.

Step5.计算2次迭代之间的估计误差,如果|RMSEη+1-RMSEη|≤χ,就终止迭代;否则返回步骤(1)进行迭代.

5 实验结果与分析

本文实验采用的是西北大学可视化研究所采集的颅面样本数据.为了验证本文算法对属性相似颅骨的配准准确度以及效率,本文用文献[22]提到的方法,在颅骨数据库中检索到38套属性相近的颅骨组成测试数据集.算法中基本参数设置如下:ξ1=0.05,ξ2=0.02,ξ3=0.01.

实验采用的PC配置为3.50GHz、内存为8GB,操作系统为Windows 7.在Matlab R2014a平台上实现了结合颅骨分区的初始配准算法和改进的ICP算法.

5.1 初始配准结果分析

本文对基于区域的自动配准、基于曲率图的配准和本文算法三种算法进行初始配准对比实验. 其中2组不同点云数据实验结果如图2和图3所示. 图2为第一组颅骨点云配准结果,图2(a)左侧为参考颅骨(13201个点),右侧为待匹配颅骨(11282个点).图3为第二组颅骨点云配准结果,图3(a)左侧为参考颅骨(102905个点),右侧为待匹配颅骨(92837个点).实验分析可知,本文算法与其他两种算法相比,本文初始配准获得的初始结果比较好.

图2 第一组数据初始配准结果Fig.2 Initial registration results of the first set of data

图3 第二组数据初始配准结果Fig.3 Initial registration results of the second set of data

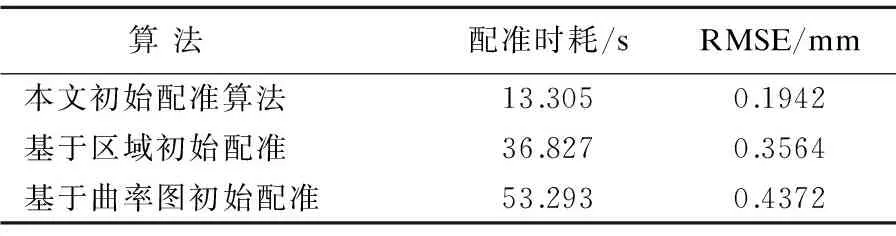
将本文中所提的RMSE作为配准准确度的评判标准.表1为图2初始配准结果的配准时耗及准确度分析,由表1和表2可知,基于区域的自配准算法和基于曲率图配准算法得到的初始配准误差比较大,第一组数据RMSE分别为0.3564mm和0.4372mm,第二组数据误差分别为0.3950mm和0.4028mm.而本文算法的到的初始配准结果比较好,第一组和第二组RMSE仅为0.1942mm和0.2184mm.基于区域的自动配准算法初始配准阶段,需要将每一个区域与剩余所有区域进行初始配准;基于曲率图的配准算法初始配准阶段,在应用曲率相似度求解匹配点对的基础上,再计算每个点的曲率图;而本文算法初始配准阶段应用Euclidean距离相似度和KNN算法求解相似区域与匹配点对,只需要将一个区域与相似的几个区域进行配准即可.因此,本文算法与其他两种算法相比,有效的降低了初始配准阶段的时间复杂度.

表1 第一组数据初始配准算法对比
Table 1 Comparison of the first set of data registration algorithm

算法 配准时耗/sRMSE/mm本文初始配准算法13.3050.1942基于区域初始配准36.8270.3564基于曲率图初始配准53.2930.4372

表2 第二组数据初始配准算法对比
Table 2 Comparison of the second set of data registration algorithm

算法 配准时耗/sRMSE/mm本文初始配准算法31.9380.2184基于区域初始配准69.5710.3950基于曲率图初始配准74.9050.4028

5.2 精确配准结果分析

在初始配准算法的基础上,对基于区域中的稀疏ICP算法、基于曲率图中的经典ICP算法和本文算法的配准准确度和配准时耗,做了对比实验,实验结果如图4-图5所示.

图4 第一组数据精确配准结果对比Fig.4 Comparison of accurate registration results from the first set of data

由图4(a)和图5(a)分析可知,基于曲率图中的经典ICP算法,可以大幅度提高配准的准确度,但是该算法的配准结果出现了局部最优的现象.由图4(b)和图5(b)显示,基于区域中的稀疏ICP算法的精确配准,大部分区域有效的提高了配准的准确度,但是部分区域(下颚、脸颊)出现了误配或错配的现象.

图4(c)显示,在Destimation不同取值的情况下,当λ=3时,配准的准确度平均达到了89.83%;当λ=2时,配准的准确度平均达到了82.71%,额头和脸颊部分出现错配;当λ=1时,配准的准确度平均达到了73.63%,但是基于区域中的稀疏ICP与本文算法相比,配准效果更好,由图可知,眼睛和下颚部分出现错配以及误配.由图4(c)可知,在λ=3时,本文算法与基于区域中的稀疏ICP和基于曲率图中的经典ICP算法相比,配准的准确度平均提高了15.26%和19.13%.图5(c)显示,在Destimation不同取值的情况下,当λ=3时,配准的准确度平均达到了91.70%;当λ=2时,配准的准确度平均达到了80.95%,下颚区域出现错配;当λ=1时,配准的准确度平均达到了72.43%,右眼及下颚部分出现错配以及误配.由图可知,在λ=3时,本文算法与基于区域中的稀疏ICP和基于曲率图中的经典ICP算法相比,配准的准确度平均提高了16.82%和20.01%.由此说明本文提出的算法是有效可行的,在Destimation不同取值情况下,灵活有效的提高了配准的准确度,降低了配准时间复杂度.

图5 第二组数据精确配准结果对比Fig.5 Comparison of accurate registration results from the second set of data

表3和表4分别为图4和图5的配准时耗和配准的RMSE,由表3和表4可知,基于曲率图中的经典ICP的配准算法耗时较大,配准的RMSE分别为0.0829mm和0.0764mm.基于区域中的稀疏ICP,配准时耗与本文算法相比,配准时耗比较大,配准准确度比本文算法λ=1时好,但当λ=2和λ=3时,本文算法比基于区域中的稀疏ICP好.因此可知,与前两种算法相比,本文配准效率整体得到了进一步提高,本文提出的算法有效的提高配准的准确度.

为了验证本文算法的有效性和可行性,在初始配准的基础上,对基于曲率图中的经典ICP算法、基于区域中的稀疏ICP和本文改进ICP算法(λ=3)三种算法,在不同迭代次数下进行了误差统计分析.实验结果如图6所示.

表3 第一组精确配准算法对比
Table 3 Comparison of the first set of data Accurate registration algorithms

算法RMSE/mm配准时耗/s基于曲率图经典ICP0.0829135.574基于区域稀疏ICP0.0453105.570λ=30.0237本文算法λ=20.042671.968λ=10.0489

表4 第二组精确配准算法对比
Table 4 Comparison of the second set of data Accurate registration algorithms

算法RMSE/mm配准时耗/s基于曲率图经典ICP0.0764173.293基于区域稀疏ICP0.0372146.827λ=30.0261本文算法λ=20.0354λ=10.0493109.736

由图6看出,当iteration>35时,本文算法的RMSE趋于稳定,而基于区域中的稀疏ICP算法和基于曲率图中的经典ICP算法,当iteration≥45时才趋于稳定.因此,本文改进的ICP算法与稀疏ICP算法和基于曲率图中的经典ICP算法相比,收敛速度更快,配准的时间复杂度大大减小.当iteration=45时,本文改进的ICP算法的配准误差比基于区域中的稀疏ICP算法提高了很多,与基于曲率图中的经典ICP算法相比,配准的准确度大大提高.说明本文用提出的Destimation来剔除误匹配点对的方法有效可行.本文算法不仅有效降低了配准的时间复杂度,还提高了配准的准确度.

图6 不同迭代次数下的RMSE分析Fig.6 RMSE analysis of different iteration times

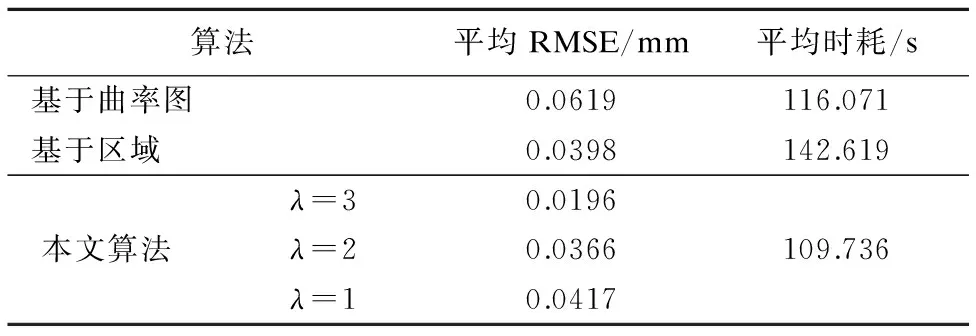
为了更加直观的对比这三种方法,表5显示,在38套属性相近的颅骨测试数据集上,分别采用基于区域配准算法、基于曲率图的配准算法和本文算法进行配准,并根据实验结果,统计三种算法的平均配准误差以及平均配准时耗.

分析图4-图5和表5可知,基于曲率图的的配准算法寻找匹配点对的过程比较简单,此方法主要是计算曲率,根据每个点的曲率值构造曲率图,并根据曲率图寻找匹配点,即需要计算颅骨模型中的所有点的曲率构造曲率图以及待匹配颅骨中点到参考颅骨中所有点的曲率图的加权距离,然后取距离最短的m个点作为潜在匹配点,这个计算过程十分费时,大大增加了算法的时间复杂度,又由于几何约束条件太少,导致此方法配准的准确度降低,该方法精确配准部分应用经典ICP算法,即采用基于Euclidean距离的最近点对应方法寻找匹配点,而且对匹配点对没有进行筛选,容易出现错配现象,导致配准准确度大大降低.采用基于区域的自动配准算法,该方法首先需要将颅骨样本进行区域划分,然后对待匹配颅骨

表5 不同配准算法的平均误差
Table 5 Average error of different registration algorithms

算法平均RMSE/mm平均时耗/s基于曲率图0.0619116.071基于区域0.0398142.619λ=30.0196本文算法λ=20.0366109.736λ=10.0417

中的区域与参考颅骨中所有区域进行配准,这个过程计算复杂,使得配准的时间复杂度大大增加,精确配准阶段采用稀疏ICP算法,该算法采用稀疏诱导范式代替经典ICP算法中的二范式,虽然使得匹配点对的准确度增加,但是依旧没有进行误匹配点对的筛选,而且还需要计算待匹配颅骨中的点到参考颅骨中所有点的稀疏诱导范式,这个计算过程,大大增加了配准的时间复杂度,降低了配准的准确度.本文算法采用Euclidean距离相似度等几何特征作为约束条件,根据KNN算法以区域质心作为配准单位减少待匹配颅骨中区域与参考颅骨区域配准的区域数目,减少了计算量,大大提高配准效率,精确配准阶段,采用kd-tree算法,有效的缩小了待匹配颅骨在参考颅骨中寻找匹配点的范围,并且提出Destimation对匹配点对进行筛选,有效剔除了误匹配点对,减少了计算量,降低了配准的时间复杂度,提高了配准的准确度.实验表明,分别采用这三种方法进颅骨配准,本文算法的配准时耗是基于曲率图配准算法的20%,是基于区域配准算法的16%,配准配准的准确度是其他两种方法的2倍之余.

6 总 结

本文提出了结合分区和改进ICP的颅骨自动配准算法.首先在初始配准阶段,进行颅骨分区,有效避免了特征点的标定以及曲率等几何特征的计算,并运用基于质心的区域匹配得到相似的区域对,运用RANSAC算法得到最优变换矩阵.然后进行精确配准,初始配准为此阶段提供了良好的初始值,避免了算法陷入局部最优,运用kd-tree算法寻找匹配点,并提出Destimation来剔除误配的匹配点对.实验表明,本文算法能有效缓解颅骨配准过程中出现的效率低和准确度不高的问题,满足颅面复原中的颅骨形态统计要求.

[1] Shui Wu-yang,Zhou Ming-quan,Wu Zhong-ke,et al.An approach of craniofacial reconstruction based on registration [J].Journal of Computer-Aided Design & Computer Graphics(CAD&CG),2011,23(4):607-614.

[2] Besl P J,Mc Kay N D.A method for registration of 3-D shapes[J].IEEE Transactions on Pattern Analysis and Machine Intelligence(PAMI),1992,14(2):239-256.

[3] Medioni G,Chen Y.Object modeling by registration of multiple range images[J].Image & Vision Computing,1992,10(3):145-155.

[4] Wang Xin,Zhang Ming-ming,Yu Xiao,et al.Point cloud registration based on improved iterative closest point method[J].Opticsand and Precision Engineering,2012,20(9):2068-2077.

[5] Liu Chun-guo,Liu Chang,An Bai-ling.Three dimensional surface registration on the basis of genetic algorithm[J].China Metal Forming Equipment & Manufacturing Technology,(CMET),2009,44(4):110-113.

[6] Ko K H,Maekawa T,Patrikalakis N M.An algorithm for optimal free-form object matching [J].Computer-Aided Design,2003,35(10):913 -923.

[7] Zhu Yan-juan,Zhou Lai-shui,Zhang Li-yan.Registration of scattered cloud data[J].Journal of Computer-Aided Design & Computer Graphics(CAD&CG),2006,18(4):475-481.

[8] Ge Bao-zhen,Peng Bo,Tian Qing-guo.Registration of three-dimensional point-cloud data based on curvature map [J].Journal of Tianjin University,2013,46(2):174-180.

[9] Zhao Fu-qun,Zhou Ming-quan,Geng Guo-hua.Point cloud registration algorithm based on bounded rotation angle[J].Microelectronics & Computer,2017,34(3):46-49.

[10] Zhang C,Du S,Liu J,et al.Robust 3D point set egistration using iterative closest point algorithm with bounded rotation angle[J].Signal Processing,2016,120(C):777-788.

[11] Du H,Geng G,Li K,et al.3D skull registration based on registration points automatic correspondence[C].International Conference on Virtual Reality and Visualization(ICVRV),IEEE,2013,8768 (12):293-296.

[12] He Yi-yue,Ma Zi-ping,Gao Ni,et al.Local craniofacial morphological relationship modeling based on physiological registration of vertices[J].Computer Engineering and Applications(CEA),2016,52(13):19-24.

[13] Berar M,Desvignes M,Bailly G,et al.3D meshes registration:application to statistical skull model[J].Lecture Notes in Computer Science(LNCS),2004,3212(1):100-107.

[14] Sahilliog?Lu Y,Kavan L.Skuller:a volumetric shape registration algorithm for modeling skull deformities[J].Medical Image Analysis,2015,23(1):15-27.

[15] Song Wei-yan.RANSAC algorithm and its application in remote sensing image processing[D].Beijing:North China Electric Power University,2011.

[16] Papazov C,Burschka D.An efficient RANSAC for 3D object recognition in noisy and occluded scenes[C].Asian Conference on Computer Vision(ACCV).Springer-Verlag,2010,6492:135-148.

[17] Han Bao-chang,Cao Jun-jie,Su Zhi-xun.Automatic point clouds registration based on regions [J].Journal of Computer-Aided Design & Computer Graphics(CAD&CG),2015,(2):313-319.

[18] Brandes U,Cornelsen S,Pampel B,et al.Blocks of hypergraphs:applied to hypergraphs and outerplanarity[C].International Conference on Combinatorial Algorithms,Springer-Verlag,2010:201-211.

[19] Bouaziz S,Tagliasacchi A,Pauly M.Sparse iterative closest point[J].Computer Graphics Forum,2013,32(5):113-123.

[20] Li W,Song P.A modified ICP algorithm based on dynamic adjustment factor for registration of point cloud and CAD model[J].Pattern Recognition Letters,2015,65(1):88-94.

[21] Senin N,Colosimo B M,Pacella M.Point set augmentation through fitting for enhanced ICP registration of point clouds in multisensor coordinate metrology[J].Robotics and Computer-Integrated Manufacturing,2013,29(1):39-52.

[22] Wang Meng-yang.Research and implementation of partition-interpolation craniofacial reconstruction method based on knowledge base[D].Xi′an:Northwest University,2010.

附中文参考文献：

[1] 税午阳,周明全,武仲科,等.数据配准的颅骨面貌复原方法[J].计算机辅助设计与图形学学报,2011,23(4):607-614.

[4] 王 欣,张明明,于 晓,等.应用改进迭代最近点方法的点云数据配准[J].光学精密工程,2012,20(9):2068-2077.

[5] 刘纯国,刘 畅,安百玲.基于遗传算法的三维曲面配准[J].锻压装备与制造技术,2009,44(4):110-113.

[7] 朱延娟,周来水,张丽艳.散乱点云数据配准算法[J].计算机辅助设计与图形学学报,2006,18(4):475-481.

[8] 葛宝臻,彭 博,田庆国.基于曲率图的三维点云数据配准[J].天津大学学报,2013,46(2):174-180.

[9] 赵夫群,周明全,耿国华.基于有界旋转角的点云配准算法[J].微电子学与计算机,2017,34(3):46-49.

[12] 贺毅岳,马自萍,高 妮,等.生理点配准的颅面局部形态关系建模[J].计算机工程与应用,2016,52(13):19-24.

[15] 宋卫艳.RANSAC算法及其在遥感图像处理中的应用[D].北京：华北电力大学,2011.

[17] 韩宝昌,曹俊杰,苏志勋.一种区域层次上的自动点云配准算法[J].计算机辅助设计与图形学学报,2015，(2):313-319.

[22] 王孟阳.基于知识库的分区插值颅面复原方法研究与实现[D].西安：西北大学,2010.