一种低信噪比条件下的调制识别方法

王 灿，范晓光，谷琼琼，张一凡

(上海无线电设备研究所，上海201109)

0 引言

通信信号调制方式识别主要通过不同调制方式之间的差异，提取信号的特征参数，进而实现信号的调制方式识别。在复杂的电磁环境下，传统的通信侦查手段已经难以满足现代战场的需求，为了及时、准确、全面地获取战场的技术情报，以确保在关键时刻对关键的通信设备及载体进行监视和干扰，传统的采用简单的特征参数调制方式识别技术，如调制参数、载频、带宽、码元速率、电平，已经无法适应实际情况的需求。因此，如何在复杂的、低信噪比的电磁环境下有效的识别出信号调制方式，无论在军事或民用领域，都具有重要的意义。

目前，在调制方式识别领域，在信噪比大于5 d B的条件下，分类方法较多。但是在低信噪比下，信号特征的鲁棒性较差，特征距离较小，目前已有的方法难以取得令人满意的分类效果。1995年，文献[1-2]通过提取信号在时域和频域上的七个瞬时特征参数作为信号的识别参数，算法虽然简单，但是在低信噪比下，特征距离小，达不到预期的效果。2000年，文献[3]提出提取数字信号的累积量特征，构造四阶矩类实现信号分类，但是该算法在低信噪比下可识别的信号类型少，且鲁棒性差。

分类器设计主要是对提取的调制特征，通过阈值设定、关联计算、训练测试等过程，来判断特征所属的类别。常见的分类器有假设检验分类器[4]、模式识别匹配分类器和人工神经网络分类器等[5，6]。证据理论是一种关于不确定性推理的重要方法，它可用于目标检测、分类和识别[7-8]。

本文针对低信噪比下数字信号调制识别问题，提出了一种多维融合熵的分类方法，通过算法设计与仿真，实现2FSK、4FSK、8FSK、BPSK、QPSK、MSK信号在低信噪比下的分类与识别。

1 熵值特征提取算法

特征提取是调制识别的关键步骤，通过对接收信号的变换，使信号之间特征区分明显，尽可能集中表征显著类别差异的模式信息。信息熵能定量描述信号的不确定性，在各个交叉领域应用广泛，如故障诊断、信号识别等。从微观上看，一个系统有序程度越高，则熵就越小，所含的信息量就越大[9，10]。

1.1 信息熵算法

设一个有n个随机事件的概率系统X=(X1，X2，…Xn)，第i个随机事件Xi出现的概率为Pi(i=1，2，…n)，且满足∑ni=1Pi=1，第Xi事件出现可以提供的信息量为H(Xi)=-Pilog2Pi，单位为bit，那么n个随机事件产生的平均信息量，即信息熵为

1.2 信息熵算法

信号的频率结构往往体现了信号丰富的内部特征和状态变化。因此将时域信号变换到频域，分析其频谱的细微特征可以更好的体现信号的信息量。常用的频谱分析方法有两种：一种是先计算信号的自相关函数，由自相关函数估计频谱;另一种是先对信号进行傅里叶变换，由傅里叶变换序列估计频谱。

信号用{xi，i=1，2，…，N}表示，经过离散傅里叶变换后，可以得到信号的离散傅里叶变换X(ωi)，ωi为第i个频率点，则信号的功率谱密度为

将功率谱密度归一化，得到功率谱密度的分布函数为

则信号的功率谱熵为

1.3 奇异谱熵算法

奇异谱熵是一种典型的时域信息熵[11]，它从信号奇异性角度分析信号的局部细微特征。设某时刻接收端同时采集到L个通道传来的信息，用Xt={x1(t)，x2(t)，…xL(t)}来表示接收信息序列。对于某个通道的信号，采样后的信号为{xi，i=1，2，…N}，采样点数为N。

为了全面分析奇异性信息，先用长度为M的分析窗口对采样信号序列进行分析。假定分析窗口的时延参数为l，则分析窗可将信号序列xi分为N-M段数据，形成(N-M)×M维的轨迹矩阵A。

i时刻所有L个通道数据的轨迹向量为

对矩阵A进行奇异值分解，设分解后得到xi的奇异值谱为{δi，1≤i≤N-M}。各个奇异值δi的大小体现了对应的模式在总模式中的比例。时域信号的奇异谱熵为

式中：pi为第i个奇异值在整个奇异值谱中所占的比重。

1.4 小波熵算法

小波是分析非平稳信号的一种工具[12]。与传统的傅里叶分析不同，小波分析可以自适应地调整分析窗口的大小，实现对信号的多分辨率分析。

对于待分析的信号f(t)，其连续小波变换表示为

相应的小波逆变换为

实际应用中，小波变换采用Mallat快速算法，它是一种既能快速实现小波变换，又能完全重构信号的方法。选取小波变换尺度为j，信号分解为低频部分cj和高频部分d1，d2，…dj共(j+1)个分量，利用式(1)对每个小波分量系数进行傅里叶变换

其中

每一层小波系数的功率谱{sk，k=1，2，…，j+1}可由式(3)估计得

因此，第k(k=1，2，…，j+1)个分量的小波熵为

1.5 信号熵值提取仿真

仿真信号类型分别是2FSK，4FSK，8FSK，BPSK，QPSK，MSK。仿真参数如下：信号长度x(t)选取2 048个点，码元速率fd=1 000 Sps，载波频率fc=4 MHz，采样频率fs=16 MHz，传输信道噪声为加性高斯白噪声。对信号进行离散傅里叶变换，奇异值变换以及Mallat小波变换，分别计算出信号在不同信噪比下的功率谱熵，奇异谱熵以及小波熵。图1是六种数字信号的熵值特征随信噪比变化曲线图。

从图1可以看出，不同信号的熵值特征不同，但是变化趋势都是相似的。在信噪比大于10 d B情况下，信号熵值曲线趋于稳定。在-5 d B＜SNR＜10 dB区间内，虽然数字信号熵值特征随信噪比增加而下降，但是其特征距离以及鲁棒性都很好，可以作为低信噪比下数字信号的识别特征。对比图1(a)、图1(b)、图1(c)，可以看出不同熵值对不同数字信号的特征距离不同。

功率谱熵对2FSK，MSK和8FSK信号有较好的区分能力。奇异谱熵值特征能将8FSK，4FSK和信号QPSK分离，并且可以将MSK和BPSK归为一类。而小波熵对MSK和2FSK信号有较好的区分能力。因此，可以对这三种熵值特征进行组合，实现对这几种数字信号调制方式的分类识别。

2 分类器设计

分类器设计主要是对提取到的调制特征，通过阈值设定、关联计算、训练测试等过程，判断特征所属的类别。证据理论是一种关于不确定性推理的重要方法，它可用于目标检测、分类和识别，本文通过证据理论设计了一种多维融合熵的分类方法。

2.1 证据理论

1967年，Dempster给出了用概率区间描述信息不确定性，以及证据之间的融合表达算法。之后，Shafer进一步完善，建立了命题和集合之间的对应关系，将命题的不确定问题转化为集合的不确定问题。证据理论在专家系统、特征识别等方面具有广泛的应用，在多传感器信息融合领域已经成为了一种重要的方法[13-15]。

完备集Θ又称作识别框架，即Θ={θ1，θ2，…，θN}，在完备集Θ下，BPA函数m幂级2Θ到[0，1]的映射，用A表示Θ的任意子集，即A⊆Θ，则m满足条件：

式中：m(A)为命题A的BPA函数，它描述了证据对命题A的支持概率权值。如果m(A)＞0，则称A为焦元。

在识别框架Θ={θ1，θ2，…，θN}下，用E1和E2表示两个证据，其相应的BPA为m1和m2，焦元为Ai和Bj。

如果

则D-S合成规则为

其中：

称为冲突系数，体现了证据之间的冲突程度。

对 于 多 组 证 据{m1(A)，m2(A)，…，mK(A)}，其融合式为

2.2 决策规则

决策需要根据融合分类器输出的融合概率赋值函数。设存在A1，A2⊂U且满足：

若有

则A1为判决结果，其中ζ为设定的阈值。

2.3 基本概率赋值函数获取

基本概率赋值函数的获取是证据理论在目标识别领域的关键步骤。在提取了数字信号熵值特征的基础上，本文获取基本概率赋值函数方法如下：

a)求取信号熵值特征向量Hi×j，i=1，2，3代表不同的熵值特征，j=1，2，…6代表信号类型2FSK，4FSK，8FSK，BPSK，QPSK，MSK;

b)求熵值特征的均值μi×j=MEAN(Hi×j)，方差σi×j=var(Hi×j);

c)输入一个待识别信号x(t)，并提取信号熵值特征hi，i=1，2，3代表不同的熵值特征;

d)根据待识别信号的熵值特征与熵值库的特征距离可以计算出不同熵值的权值矩阵m(pi)。

由此可得

通过归一化，可以得到信号的BPA函数

3 仿真实验

仿真过程中选取6种常见的数字调制信号，分别 是2FSK、4FSK、8FSK、BPSK、QPSK、MSK，仿真参数不变。在不同的信噪比下，提取信号的功率谱熵，奇异谱熵以及小波熵，并用本文的证据理论分类器进行分类识别。仿真过程中，在每个信噪比下，每个信号做500次的蒙特卡洛实验，D-S决策阈值ε=0.1，计算不同信噪比下信号的识别性能如表1所示。由表1可见，在SNR＞-5 d B时，信号识别能达到78%以上，在SNR＞0 dB时，信号识别率能达到97%以上。实验结果表明，本文提出的多维融合熵识别方法可以在低信噪比下对多种数字信号进行有效的识别。

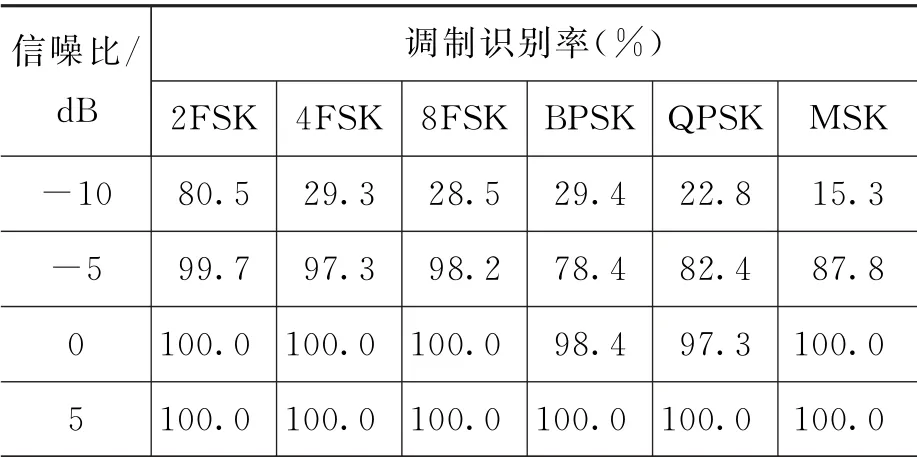
表1 数字信号调制识别率

4 结论

在低信噪比条件下，本文通过提取信号的功率谱熵，奇异谱熵以及小波熵值特征，验证了熵值特征作为数字信号特征分类的有效性。通过设计一种融合分类器，提出一种多维融合熵分类方法，实现了低信噪比下多种数字调制信号的分类识别。仿真结果表明，在SNR＞-5 dB时，信号识别能达到78%以上，在SNR＞0 d B时，信号识别率能达到97%以上。