三角波调频雷达频谱配对新方法

宋卫东，李 松，尹 辉，史方明

(上海无线电设备研究所，上海201109)

0 引言

三角波调频雷达又称为三角调频连续波雷达，是工程上应用非常广泛的一种线性调频连续波雷达。在三角波雷达信号处理流程中，传统的频谱配对方法由于存在FFT栅栏效应，差频信号的频率估计并不准确，进而影响到测量精度[1-3]。本文将能量重心频谱校正算法引入到雷达信号处理流程中，提出新的频谱配对方法即能量重心配对法，并针对能量重心配对法存在的估计值浮动较大的问题，进一步提出了优化的能量重心配对法，更适用于要求雷达系统测量精度较高，误差浮动较小的应用场合。

1 离散频谱校正技术

根据理论分析，差频信号可以近似为单频正弦信号，而当前离散频谱校正技术的研究主要集中在单频信号以及频率间隔较大的多频信号中[4]，所以可以将离散频谱校正技术引入到雷达信号处理中，用于校正差频信号频谱的特征参数(幅值、频率)，进而提升测距测速的精度。

当前主流的三种频谱校正技术，分别是插值校正法、相位差校正法和能量重心校正法。将离散频谱校正技术与频谱配对算法相结合，有很多种可选的组合。由于噪声和杂波具有随机性，一般情况下可认为不会引起能量重心的偏移，幅值上的叠加也是均匀的。所以，能量重心法最适合引入到雷达信号处理流程中，与频谱配对算法最为契合。

能量重心校正法又称为能量重心法。能量重心校正法的工作原理是根据加窗FFT时所选的窗函数的频谱(功率谱)的能量分布特性来推导相对频偏值和归一化的频率值。

由公式(1)可知，加窗后直接FFT法得到的频谱的最高峰谱线幅值为，最高峰谱线幅值求平方即可得到其能量为[5]

式(2)表明，离散窗谱的能量重心无穷趋近于坐标轴的原点。

在实际的工程应用中，不可能采用无限数目的频谱(功率谱)的谱线用于频谱校正，因为大多数窗函数的旁瓣都比较小，能量大多数集中在主瓣内，旁瓣的功率谱的幅值很小，所以选用主瓣内的功率谱(幅值)较大的若干条(通常选3～5条)谱线就可以使能量重心落在频谱(功率谱)的主瓣中心或者主瓣中心附近[6]。

当选用主瓣内M条谱线做频谱校正时，由式(2)可得

整理可得

另外，计算频谱(功率谱)最高峰谱线附近的几条次高峰谱线的能量和，得到

代入式(2)可得

整理式(6)，可得到相对频偏δ和归一化频率值λ^的表达式如下

由式(7)可知，最高峰谱线附近的几条谱线的能量重心即为校正后的归一化频率，即能量重心校正法的校正公式[7-8]。

2 能量重心配对法

为了提高雷达测量精度，本文将能量重心校正法与频谱配对法相结合，提出了能量重心配对法。能量重心配对法的简要原理：差频信号FFT频谱经过能量重心校正法处理后，得到的差频信号频谱的能量重心的频率和幅值，然后依据能量重心的频率和幅值，利用频谱峰值配对法的原理进行频谱配对。

为使能量重心校正法应用到雷达信号处理流程中，应充分研究能量重心校正法的性能，并对能量重心校正法在雷达信号处理中的不足提出优化的方案。

由前文知差频信号本质上是正弦信号，而正弦信号是窄带信号，其频谱的能量主要集中在真实频率频谱的主瓣内，常用的能量重心法选取主瓣内若干条幅值较大的谱线进行频谱的精确估计，下面给出常用窗函数的特性[9]。

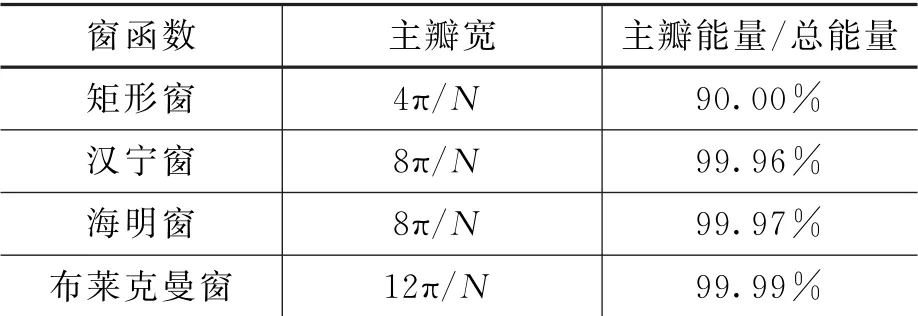
表1 常用窗函数的特性

工程上，能量重心法常常使用旁瓣衰减较快的汉宁窗，以频谱最高峰谱线为基准，取附近的3条或者5条谱线参与能量重心法运算。采样3条谱线的参与运算的方法称为3点能量重心法，同理，采样5条谱线的参与运算的方法称为5点能量重心法[10-12]。

理论研究中，通常采用频率估计误差曲线来反映频谱校正算法的性能，其横轴为相对频偏δ，纵轴为经过校正算法而得到的归一化频率与真实的归一化频率的误差，称为归一化误差[13]。

频率估计误差曲线的仿真参数：单频正弦信号，幅值A=1，数据长度N=4 096，采样频率为fs=1 024 k Hz，则谱线间隔(频率分辨率)为Δf=fs/N=0.25 k Hz。

设信号频率fb在一个频率分辨率区间[50 k Hz，50.25 k Hz]上等间隔取21个频率点，就是将相对频偏δ(FFT频谱最高峰谱线与真实频率的频率偏差)等分为21个点。分别计算在不同的相对频偏δ的情况下，频谱校正算法在这些位置进行频谱校正得到的结果与真实频谱的误差。这样我们就能得到频谱校正算法在不同的相对频偏段对频率(或幅值)校正的性能。为了分析频谱校正算法的统计特性，在每一点进行500次仿真，计算平均的归一化频率的误差，记录仿真结果并画图。

经过仿真得到了能量重心法的频率估计误差曲线，如图1所示。

可以看到，当相对频偏为零的时候，能量重心就在真实频率处，所以使用能量重心法得到的频率估计误差理所当然的也为零，当相对频偏较小时，即在[-0.25，+0.25]区间上时，能量重心靠近真实频率，频率估计误差较小;当相对频偏更大时，能量重心逐渐远离真实频率，得到的频率估计误差很快增大。但是频率估计误差仍然控制在了较小的范围内，最大归一化频率误差为0.08。分析造成这种现象的原因，是因为在相对频偏较小时，能量重心靠近真实频率，所以使用能量重心法效果很好，但是当相对频偏增大时，能量重心逐渐远离真实频率，校正效果出现下降。

3 优化的能量重心配对法

分析能量重心校正法频率估计误差的曲线特性，当相对频偏位于[-0.25，+0.25]区间上时，信号能量相对集中，频率校正算法的性能较高;而当位于[-0.5，-0.25]或[0.25，0.5]区间上时，信号能量相对扩散，性能下降很多。

为了得到更适合雷达信号处理的离散频谱校正算法，本文提出调整相对频偏的能量重心法，本文将其称为优化的能量重心法。简要叙述优化的能量重心法的工作原理：单频信号FFT频谱经过能量重心法处理后，得到相对频偏值δ，如果相对频偏δ落在能量重心法性能较好的相对频偏段则计算结束;如果相对频偏δ落在能量重心法性能较差的相对频偏段，则通过对单频信号进行频移实现相对频偏的调整，使相对频偏δ落到能量重心法性能较好的相对频偏段。

优化的能量重心法具体实现方法：先由能量重心法得到相对频偏δ1，当相对频偏δ1位于[-0.25，+0.25]区间上时，获得的信号频率λ^=l+δ1可认为是精确的频率;否则，将信号x(n)进行频移sΔδ，得到新的相对频偏δ2，使得相对频偏δ2落到[-0.25，+0.25]区间上，即校正算法性能较高的相对频偏段，然后再用能量重心法进行频率估计，得到的校正频率减去频移sΔδ。

取Δδ=0.25，就可以将位于[-0.5，-0.25]或[0.25，0.5]区间上的δ1频移到[-0.25，0.25]区间上得到δ2。具体操作：当δ1∈[-0.5，-0.25]时，s=+1，δ1+Δδ=δ2∈[-0.25，0.25];当δ1∈[0.25，0.5]时，s=-1，δ1-Δδ=δ2∈[-0.25，+0.25]。

信号的频移公式为[8]

选择汉宁窗，5条谱线的能量重心法，则仿真算法流程设计如下：

a)对差频信号x(n)做加窗(汉宁窗)FFT运算;

b)根据能量重心校正法的原理，利用式(8)计算相对频偏δ1，若δ1∈[-0.25，+0.25]，则直接利用式(7)计算差频信号频率精确值，校正结束;

c)若δ1∈[-0.5，-0.25]或δ1∈[0.25，0.5]，则利用频移公式(9)对信号进行频移，对频移后的信号xT(n)再次做加窗(汉宁窗)FFT运算，利用能量重心校正法公式计算频移后的差频信号中心频率fb0，则准确的差频信号频率为fb=fb0-sΔδ。

利用仿真可分析优化的能量重心校正法的性能，仿真参数如前文，仿真结果如图2所示。仿真结果显示，算法效果符合优化方案的初衷，改进方法有效，可以有效的弥补能量重心校正法的不足。优化的能量重心法得到的频率估计误差浮动较小，平均的归一化频率误差约为0.02。

4 新方法流程仿真及性能分析

4.1 仿真流程设计

为了验证本文提出的能量重心配对法和优化的能量重心配对法这两种新方法的性能，需要将新方法应用到具体的雷达信号处理流程中，模拟真实的雷达信号处理过程，然后通过检验最终的测距、测速结果来进一步验证新方法的效果。所以，在本节设计了信号处理流程仿真，分别将传统的频谱配对方法和两种新方法应用到雷达信号处理流程中，通过模拟真实的信号处理流程，得到测试结果，并进行比较，分析算法性能。

能量重心配对法以及优化的能量重心配对法实现方案，就是在差频信号FFT处理和频谱配对处理中间，加上一步能量重心校正法(优化的能量重心校正法)，对差频信号的FFT频谱进行校正，得到校正后的精确的目标差频信号的频率和幅值，这一步处理称为目标特征参数校正。

所以，雷达信号处理仿真流程的设计从回波信号混频开始，接着差频信号做加窗FFT，再经过CFAR、质心凝聚、目标特征参数校正，然后频谱配对，到最后测距测速结束，得到雷达信号处理流程图如图3所示。

根据工程的实际情况选择仿真参数，使信号处理流程仿真能够在一定程度上反映工程中的情况。 仿真参数设置如下：发射信号中心频率f0=9 GHz;调制带宽B=75 M Hz;扫频周期T=4 ms;系统采样率fs=1 024 k Hz。选取5个具有代表性的仿真目标，设置每个目标的参数如表2所示。

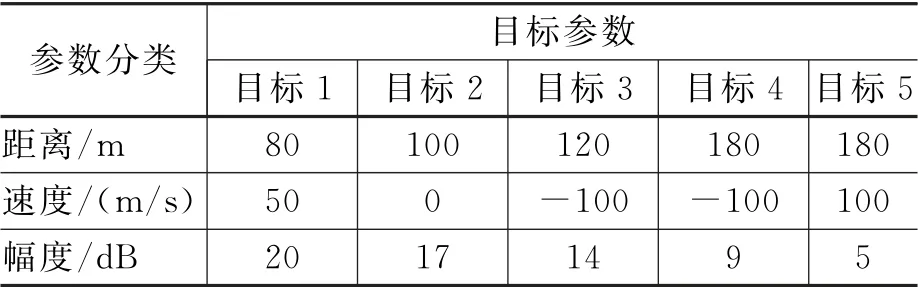
表2 目标特征参数

4.2 仿真结果及性能分析

分别执行FFT频谱峰值配对法、能量重心配对法、优化的能量重心配对法进行流程仿真，对目标1进行单次流程仿真得到的测试结果如表3所示。

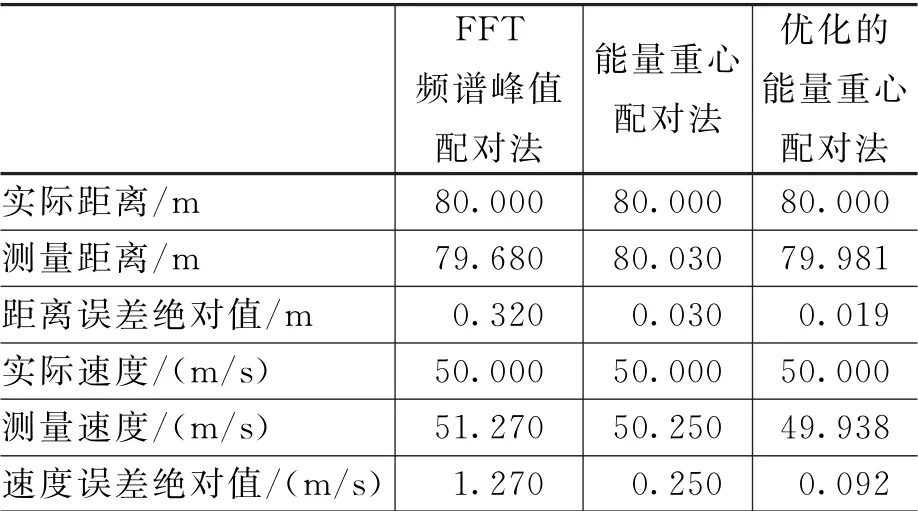
表3 三种频谱配对法对目标1单次仿真结果

单次流程仿真的结果可以看出新算法能够提升探测精度，但是每次探测结果的数据有较大波动，为了更全面的分析新算法的性能，需要做多次流程仿真，总结探测结果的统计特性。

保持雷达系统参数和目标参数不变，分别使用FFT频谱峰值配对法、能量重心配对法、优化的能量重心配对法进行仿真实验，每种方法进行20次仿真。对每一种方法得到的测试结果，计算其距离误差和速度误差的平均值和最大值，结果如表4所示。

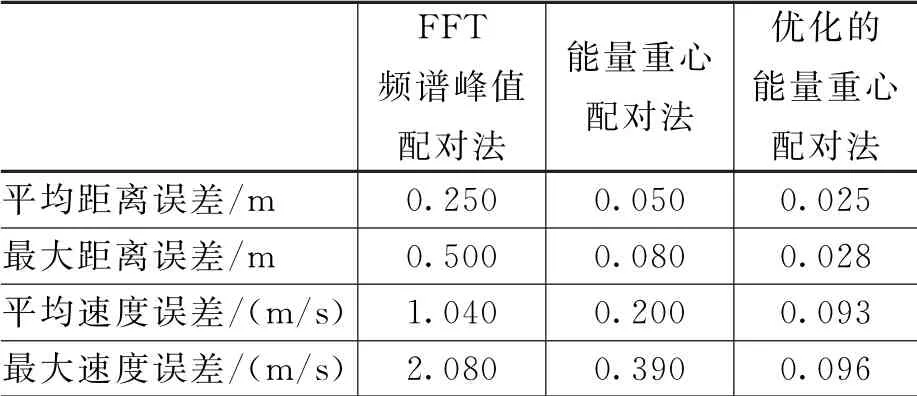
表4 测试结果统计结果

观察三种频谱配对法测距测速误差的曲线，分析测试结果的统计结果，可以得到以下结论。由于能量重心法校正了差频信号频率的精度，相比FFT频谱峰值配对法，能量重心配对法的测距最大误差下降到了原来的约16%。由于优化的能量重心法修正了能量重心法在不同相对频偏段校正性能起伏较大的缺陷，所以能量重心配对法得到的测量误差浮动较小，测距测速的最大误差接近平均误差。

算法的配对性能体现在频谱配对出现错配的概率，在一定条件下，配对性能越好，配错的概率越低，由此出现虚警的概率越低。

噪声和杂波的随机性会引起频谱幅值的随机起伏，所以，依据一条谱线的幅值信息进行频谱配对的算法，配对性能会低于依据多条谱线的幅值信息配对的算法。因此，之前的学者们在已有的最简单的依据一条谱线配对的频谱峰值配对法的基础上，进一步开发出了依据多条谱线配对的均方差法和频谱面积法。

能量重心配对法是在FFT频谱峰值配对法的基础上，增加一步能量重心法校正的处理。能量重心配对法在频谱配对处理时利用的是频谱峰值配对法的原理，表面上依据的是一条经过校正后的谱线幅值信息进行配对，但是，本质上是依据多条谱线信息进行配对。因为在使用能量重心法对差频信号FFT频谱进行校正时，依据的是信号频谱中最高的若干条(3条～5条)谱线幅值信息进行运算。而优化的能量重心配对法的原理，本质上是在能量重心配对法的基础上，多做一次能量重心法的校正处理，依据的谱线数目和能量重心配对法的一样，但是校正效果更好，更接近真实值，更利于提高配对性能。

能量重心配对法或优化的能量重心配对法这两种新方法的优势在于，同样是利用多条谱线信息进行频谱配对，两种新方法并不像均方差法和频谱面积法一样，仅仅将多条谱线的幅值信息用于频谱配对处理，新方法还同时将多条谱线的幅值信息用于校正差频信号的频率，提高频率估计精度，进而提高测量精度。

算法复杂度体现在实现算法需要的加法和乘法的次数。假设目标个数为M，配对算法依据的谱线条数为N，那么各种频谱配对算法所需运算量：频谱峰值法，需要M×M次加法;均方差法，需要N×N次加法，M×M次乘法，M×M次加法;频谱面积法，需要M×N次乘法，M×N次加法，M×M次加法;能量重心配对法，需要N×N次乘法，2 N次加法，M×M次加法;优化的能量重心配对法，需要2×N×N次乘法，4 N次加法，M×M次加法。

综上可知，能量重心配对法和优化的能量重心配对法，在并不增加太大的运算量的条件下，能够提高频谱配对性能，提高测量精度。在某些较为苛刻的探测场景中，或者是追求很高的探测效果的情况下，能量重心配对法和优化的能量重心配对法是一种不错的选择。

5 结论

本文将能量重心校正算法引入到雷达信号处理流程中，提出新的频谱配对方法即能量重心配对法，并针对能量重心配对法存在的估计值浮动较大的问题，进一步提出了优化的能量重心配对法。信号处理流程仿真证明，能量重心配对法和优化的能量重心配对法在并不增加太大的运算量的条件下，能够提高频谱配对性能，提高雷达测量精度。