基于双轴各向异性磁阻传感器电流测量系统的研究

尹 栋 ，张秀峰 ，Kian Hoong KWAN，王谷城

（1.磁浮技术与磁浮列车教育部重点实验室（西南交通大学），成都 610031；2.新加坡淡马锡理工学院清洁能源中心，新加坡529757）

近年来，工业和家庭对使用的电流传感器小型化和智能化要求越来越高，大大加快了电流传感器的升级和发展[1，2]。电流测量的主要方法包括：互感器法、罗氏线圈法、霍尔效应传感器法、磁通门传感器法和磁阻传感器法[3]。使用互感器测量电流是如今使用最多的方法，但是其体积较大，精度较低，灵敏度较低，会发生铁磁谐振，而且短路电流较大[4]；罗氏线圈与传统电流互感器CT（current transformer）相比，其体积小、不易饱和、频带宽、频率响应快、安装及维护方便、没有二次开路危险等优点，因此在现代电流及电能测量中广泛应用，但是其测量精度受导线的位置影响[5-8]；霍尔效应传感器是典型的固态元件，其寿命长，可以实现高速操作（大于100 kHz），可以工作在－40～150℃）的温度范围，但是灵敏度低，有温漂需要温度补偿，对外部压力比较敏感，大量应用于分布系统中的交流电流测量[9,10]；电阻式电流传感器具有高精度和低补偿的特性，但是当较大的尖峰电流通过采样电阻时，采样电阻可能会被烧毁[11]。磁通门传感器铁磁芯会饱和，测量磁感应强度时会产生2次谐波，要借助磁通集中器或其他补偿措施来完善，而且价格昂贵[12,13]；磁阻传感器具有体积小、灵敏度高、价格便宜等优势，随着半导线技术的发展，基于磁阻效应的各向异性磁阻AMR（anisotropic magnetoresistive）传感器被广泛应用于数字罗盘、交通状况检测系统和电流测量[14,15]中。

文献[16]中应用AMR传感器阵列建立一种基于位置估计的电流测量方法，即在1/4圆、水平和垂直方向的顶点分别放置2个正交AMR传感器；当半径为25.4 mm时，其测量精度可达到99%,但其精度受放置导线离圆心距离的影响，而且使用8个AMR传感器成本相对较高；文献[17-18]将4个具有排除周围干扰的霍尔效应传感器分别放置在对称的1/4大电缆上，用于测量三相电流，解决了传统电流传感器磁饱和的问题；文献[19]中采用3个霍效应传感器构成等边三角形，应用三角形的位置估计算法，得到接近99%的精度。

本文提出一种测量同心导线电流的新方法，整个系统仅需要两个双轴AMR传感器，更加简单可靠，不需要复杂的校准。首先建立一种新结构的传感器单元,并提出一种精确计算位置的算法，仅使用2个双轴AMR传感器。相对文献[16-19]的方法，成本较低，由于体积小可以应用于更多的场合。然后设计了适合该类传感器的输出信号的处理算法和卡尔曼滤波器，最后搭建实验平台验证了所提结构和算法的正确性。

1 电流测量系统理论模型

1.1 基本原理分析

由磁场毕奥-萨伐尔定律，一根长直导线产生同心磁力线的理论分析[20]表达式为

式中：B为磁感应强度；u0为真空磁导率；I为电流单位方向矢量；r为导线和AMR传感器之间的距离；θ为I矢量与 r矢量夹角；θ1为 I矢量与 r初始位置矢量夹角；θ2为I矢量与 r末尾位置矢量夹角。

当导线无限长时，θ1趋近-π/2，θ2趋近 π/2，则无限长导线产生的磁场强度为

可知，磁场强度与电流成正比关系,与导线到测量点的距离成反比关系。

1.2 测量模型的建立和求解

在实际测量中，测量单个导线流过的电流十分常见，在单导线电流测量的建模中通常采用单导线模型。传感器单元原理如图1所示。以O点为原点，建立笛卡尔坐标系，由原点O和A、B组成一个以O点为直角的等腰直角三角形模型，在D点放置一根穿过OAB等腰直角三角形面的长直导线，D点为等腰三角形OAB中的任意一点，则通过D点长直导线的电流在A、B分别会产生垂直和平行的磁场。

图1 传感器单元原理Fig.1 Principle ofsensor unit

式中，θa和θb分别为a点和b点磁场角度。根据θa、θb定义及位置定位算法，导线在坐标中的位置可表示为

那么通过导线在坐标的位置可以计算出导线到传感器A、B的距离分别为

则通过位置估计得到的电流为

式中：I为通过位置估计得到的电流；Voav和Voap分别为电流在a点产生的垂直电压和平行电压；Vobv和Vobp分别为电流在b点产生的垂直电压和平行电压。

2 AMR电流测量系统

2.1 传感器单元

传感器单元由分别放在A、B点的2个传感器和原点O在笛卡尔坐标系中建立一个等腰直角三角形，将传感器焊在 PCB（printed circuit board）板上进行精确定位，实现位置精确估计。传感器单元模型如图2所示。

图2 传感器单元模型Fig.2 Model of sensor unit

A、B两个传感器都是双轴传感器，分别测量由导线D中流过电流产生的磁场强度在平行于斜边和垂直于斜边的磁场强度分量。

2.2 电流估计

传感器的输出电压与其灵敏度方向产生的磁场强度成线性关系为

式中：Voi为传感器i输出电压；Bi为导线电流产生的磁场强度；si为传感器i的灵敏强度，是传感器的固有特性常数。

所以求解的电流函数可以表示为

由于采用HONEYWELL公司生产的相同型号AMR传感器，所以sa=sb=s。在实际中测得的磁场强度包含其他非导线产生的磁场强度，所以导线电流在双轴传感器上产生的电压分别为

式中：Bav、Bap和 Bbv、Bbp分别为长直导线分别在传感器 A 和 B 产生的磁场强度；Bavζ、Bapζ和 Bbvζ、Bbpζ分别为其他外部干扰磁场和噪声在传感器A和B产生的磁场强度；Vavζ、Vapζ和 Vbvζ、Vbpζ分别为其他外部干扰磁场和噪声在传感器A、B产生的输出电压。

利用角度的位置计算算法可得到实际测得电流值和由其他外部影响引起的误差项，即

2.3 信号处理算法

为了达到电流测量高精度的要求，清除Vavζ，Vapζ，Vbvζ，Vbpζ对电流测量结果的影响， 同时考虑算法的复杂性和可操作性，对于单一长直导线的测量系统，AD采样时可能发生在截取非整周期信号时发生频谱泄露和栅栏效应，影响信号分析精度，采用一些基本的窗函数（如三角窗，矩形窗）对信号加权可减少非整数周期截断造成的频谱泄漏和栅栏效应的影响，但其效果固定旁瓣比重的制约，而Kaiser-Bessel窗函数可以调整主瓣宽度和旁瓣高度间的比重，可以避免截取非整周期信号时发生频谱泄露和栅栏效应[20]。

时域内，Kaiser-Bessel窗函数可表示为

式中：N为序列的长度；I0为0阶第1类修正的Bessel函数；πα为窗函数的形状参数，πα越大衰减速率也越大。当电压频率为50 Hz，采样频率为12.5 K/s，截断信号的长度为1 375时，选用N=11，πα=5，其旁瓣衰减速率为18 dB/s，可满足精度要求。用于信号预处理的Kaiser窗函数的频域信息如图3所示。

图3 Kaiser窗函数（N=11，πα=5）Fig.3 Kaiser window function（N=11，πα=5）

2.4 卡尔曼滤波

为了达到电流测量高精度的要求，清除Vavζ，Vapζ，Vbvζ，Vbpζ对电流测量结果的影响， 同时考虑算法的复杂性和可操作性。卡尔曼滤波器用于噪音控制系统，卡耳曼滤波器也被称为线性二次估计，通过系统输入输出观测数据，对系统状态进行最优估计的算法[21,22]。根据卡尔曼滤波假设，ξ表示白噪和高斯噪声，可以得到最优的估计值。在实际情况下，如果选择合适的参数，在相似的情况下仍然可以得到较好的结果，为了设计卡尔曼滤波器，首先需要知道系统的状态空间方程，采用算法估计电流作为测量方程（15）。估计电流作为状态变量，导体与传感器的距离作为常数（当导体在虚拟三角形中时），用（n+1）和n的比率作为预测变量，电流误差作为估计误差，则信号处理的卡尔曼滤波器设计表示为

式中：Voa为传感器A的输出电压；P（n|n-1）为估计误差，ξ由外部的干扰磁场和噪声决定。则卡尔曼的更新方程为

式中：I（n|n-1）为基于（n-1）的估计值；I（n|n）为基于第n个输出变量的更新估计值；Kn为系统的设计卡尔曼增益；η为环境的测量噪声。其中I（n|n-1）可表示为

通过理论分析，得到精确的估计模型，卡尔曼滤波参数设置如表1所示。通过位置估计算法得到的估计电流为EC，经过卡尔曼滤波得到的电流为FC。其二者波形如图4（a）所示。图中，估计电流含有大量异常的高频电流，而经过卡尔曼滤波器后，这些高频电流都被移除。通过与参考电流（由霍尔传感器LEMS-LTS 25-NP测得）比较可分别得到估计电流误差（EE）和滤波电流误差（FE），二者与迭代次数的关系如图4（b）所示。

表1 卡尔曼滤波参数Tab.1 Parameters used in Kalman filter

图4 EC和FC比较及EE和FE与迭代次数关系Fig.4 Current comparison between EC and FC and their corresponding errors EE and FE

3 传感器单元与测试

3.1 传感器单元

AMR传感器单元包括AMR传感器和外围电路，如图5所示，在设计的等边直角三角形中，斜边为36 mm，2个传感器分别放在斜边的2个端点，根据设计需要采用Honeywell的双轴磁阻传感器HMC1022，其具体参数如表2所示。

图5 AMR传感器单元Fig.5 AMR sensor unit

表2 Honeywell HMC1022传感器参数表Tab.2 Specifications of honeywell HMC1022

AMR传感器外围电路包括可编程放大器PGA和置位复位电路。PGA的放大倍数选择由测量的实际磁场决定；如果磁场较小，选择较大的PGA倍数，使得输出的电压信号最佳。当AMR传感器受到强磁场干扰和温漂的影响时，通过置位复位电路可以清除这些影响。在实际的测试环境中由于电源开启的过程中产生较大磁场使传感器测得的磁场发生混乱，导致初始测试电流发生畸变，通过复位电路产生的复位电流使初始测量传感器输出电流恢复在零状态，提高抗干扰能力。

3.2 测试平台

为了验证AMR传感器单元，搭建了测试平台，如图8所示。测试平台由3个部分组成：Part 1包括传感器单元和参考电流传感器（霍尔传感器LEMSLTS 25-NP），其中参考电流传感器精度可以达到99.8%,可满足设计要求，传感器单元是用于测量电流产生磁场的原始电压信号，传感器单元上的3个测试孔，代表等边直角三角形内的任意位置方便测试导线的放置；Part 2包括测试板，主要包括导线的走线，即参考电流传感器和信号线的规划；Part 3包括常用家用电器。PC+LABVIEW包括NIc RIO-9074集成化系统，将实时处理器、可重新配置的现场可编程门阵列（FPGA）机箱和具有16位分辨率、250 kS/s总采样速率的NI 9205 AD采样模块。

3.3 实验结果与分析

所有测试电器的估计电流都含有大量的高频电流和奇异值，这些误差不仅影响电流的有效值，而且还会影响波形的傅里叶分析等。运用设计的卡尔曼滤波器对Kaiser窗和位置算法得到的电流进行处理，可得运用滤波器清除后的高频电流和奇异值。实验结果表明运用Kaiser窗、位置算法和卡尔曼滤波器可以实现电流的精确估计。在得到精确估计电流基础上，在传感器单元上的3个不同位置测试实验中每一种电器的稳态电流，测试结果如表（3）～表（5）所示。

图6 传感器单元测试平台Fig.6 Test platform of prototype sensor unit

精度定义为

式中：IF为通过卡尔曼滤波得到的电流。IR为参考电流。

由表3～表5表结果显示，在没有任何校准情况下，通过位置算法和卡尔曼滤波可以得到高精度滤波电流，这表示在虚拟的等腰直角三角形中任意点位置使用本文方法可以得到高精度的电流估计值，解决了在磁传感器应用中需要每次校准的问题。

表3 位置1的测试结果Tab.3 Results at position 1

表4 位置2的测试结果Tab.4 Results at position 2

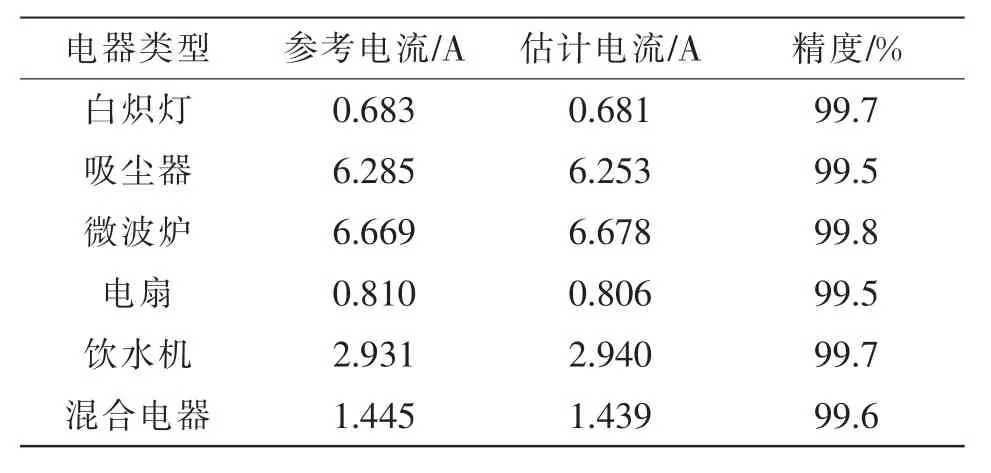
表5 位置3的测试结果Tab.5 Results at position 3

4 结语

本文提出一种新的测量电流的传感器单元结构和定位算法，仅需2个双轴各向异性磁阻AMR传感器。通过测得磁场强度之间角度和导线位置进行准确定位，根据传感器输出电压信号的特性运用Kaiser窗函数对信号进行预处理，设计卡尔曼滤波器对预处理的信号进行滤波处理,减小外部干扰磁场和噪声的影响，得到误差低于1%的电流波形。通过测量传感器单元上的不同位置流过导线的电流，验证了定位算法在测量中不需要校准结论。通过测量一些常用电器工作电流大小，考虑参考电流传感器 （霍尔传感器LEMS-LTS 25-NP）的测量精度，AMR传感器电流测量系统的精度可以达到95%以上。后续工作将提高其在电力系统大电流导线产生强磁场影响下的抗干扰处理能力，将传感器单元、MPU（microprocessor unit）处理单元，显示单元集成在PCB上，开发出一款新的便携式电流传感器。提出的位置算法还可应用对导线位置要求严格的其他场合。

参考文献：

[1]Zhang Ruihua,Du Yumei,Liu Yuhong.New challenges to power system planning and operation of smart grid development in China[C].Power System Technology（POWERCON）,2010 International Conference on,2010:1-8.

[2]Wang Jifeng,Zhou Huafeng.Conceptual design and the future development for operation smart system in china southern power grid[J].IEEE Transactions on Smart Grid,2013,4（3）:1621-1629.

[3]Vopalensky M,Platil A.Temperature drift of offset and sensitivity in full-bridge magnetoresistive sensors[J].IEEE Transactions on Magnetics,2013,49（1）:136-139.

[4]Cataliotti A,Cara D D,Emanuel A E,et al.Current transformers effects on the measurement of harmonic active power in LV and MV networks[J].IEEE Transactions on Power Delivery.,2011,26（1）:360-368.

[5]Ward D A,Exon J L T.Using Rogowski coils for transient current measurements[J].Engineering Science and Education Journal,1993,2（3）:105-113.

[6]Barber J P.The use of rogowski coils in current measurement[C].2014 17th International Symposium on Electromagnetic Launch Technology（EML）,2014:1-4.

[7]Abdi-Jalebi E,McMahon R.High-performance low-cost Rogowski transducers and accompanying circuitry[J].IEEE Transactions on Instrumentation&Measurement,2007,56（3）:753-759.

[8]Chiampi M,Crotti G,Morando A.Evaluation of flexible Rogowski coil performances in power frequency applications[J].IEEE Transactions on Instrumentation&Measurement 2011,60（3）:854-862.

[9]Ramsden E.Hall Effect Sensor:Theory and Application[M].2nd ed.Burlington,MA,USA:Newnes,2006.

[10]Sriratana W,Murayama R.Application ofhall effect sensor:A study on the influences of sensor placement[C].Industrial Electronics（ISIE）,2013 IEEE International Symposium on,2013:1-5.

[11]Nakanishi M,Kinoshita J,Sakamoto Y,et al.Current dependence measurement of 1 Ω standard resistors using a cryogenic current source with linear output[J].IEEE Transactions on Instrumenta-tion and Measurement,2001,50（2）:255-258.

[12]Pollarolo A,Jeong T,Benz S P,et al.Johnson noise thermometry measurement of the boltzmann constant with a 200Omega sense resistor[J].IEEE Transactions on Instrumentation and Measurement,2013,62（6）:1512-1517.

[13]Emerging Technologies Working group,Power systems instrumentation and measurements committee,Fiber optic sensors working group,et al.Optical current transducers for power systems:A review[J].IEEE Transactions on Power Dilivery,1994,9（4）:1778-1788．

[14]Roumenin C S.Magnetic sensors continue to advance towards perfection[J].Sensors and Actuators A Physical,1995,46（1）:273-279．

[15]Ramon V C G.Antonio G C,Marta P C,et al.Improving similarity measures for re-identification of vehicles using AMR sensors[C].2013 9th International Conference on Information,Communications and Signal Processing（ICICS）,2013:1-5.

[16]Li Xisheng,You Jia,Shu Xiongying,et al.Electric current measurement using AMR sensor array[C].International Conference on Mechatronics and Automation,ICMA 2009.2009:4085-4089.

[17]Chen Kunlong,Chen Nanming.A new method for power current measurement using a coreless hall effect current transformer[J].IEEE Transactions on Instrumentation and Measurement,2011,60（1）:158-169.

[18]Ajbl A,Pastre M,Kayal M.A fully integrated hall sensor microsystem for contactless current measurement[J].IEEE Sensors Journal,2013,13（16）:2271-2278.

[19]Chan J Y C,Tse N C F,Lai L L.A coreless electric current sensor with circular conductor positioning calibration[J].IEEE Transaction on Instrumentation and Measurement,2013,62（11）:2922-2928.

[20]George K,Chen C I H,Tsui J B Y.Extension of two-signal spurious-free dynamic range of wideband digital receivers using kaiser window and compensation method[J].IEEE Transactions on Microwave Theory and Techniques,2007,55（4）:788-794.

[21]Kalman R E.A new approach to linear filtering and prediction problems[J].Journal of Basic Engineering Transactions,1960,82:35-45.

[22]Simon D.Kalman filtering with state constraints:a survey of linear and nonlinear algorithms[J].IET,Control Theory&Applications,2010,4（8）:1303-1318.