一种新型无电解电容Buck-Boost正反激LED驱动电路的研究
曾怡达,朱仁伟,唐 丽,李 宝
(西南交通大学电气工程学院,成都 610031)
传统照明一般采用白炽灯、荧光灯等照明器材,但是白炽灯效率低且能耗高,荧光灯寿命短且存在环境污染等问题。近年来,LED照明技术得到了迅速发展,在使用寿命、节能环保和应用条件等方面均大大优于传统照明器材。
相对于两级式LED驱动电路而言,单级LED驱动电路由于其结构简单、效率高和成本低等优点更适合作为LED照明应用。传统Buck-Boost反激式PFC变换器[1,4]的PFC级和DC/DC级同时在DCM模式下工作时,其电路具有本质的PFC特性,功率因数高,并且中间级储能电容只与输入电压、输入电感和变压器原边的电感相关,与开关频率、占空比、负载无关。加入漏感回馈回路可以将漏感能量回馈到输入端,提高了变换器的工作效率。其去除电解电容的设计理论基础为
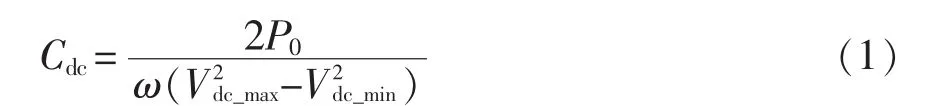
式中:P0为变换器的输出功率;Cdc为变换器的中间级电容;Vdc_max、Vdc_min分别为中间级电容电压的峰值和谷值;ω为电网角频率。
变换器的输出电压电流纹波依赖于中间级电容输入纹波Vdc的大小,即Vdc_max-Vdc_min不能过大。可以看出在限制了中间级电容的情况下,输出电压电流纹波只依赖于输出电容进行滤波,导致其输出功率不能太大。因此此电路拓扑只适用于很小功率的场合。在文献[4]中,实验样机只做到了5 W,输出纹波率已经有20%。所以传统单极Buck-Boost反激变换器只能用于小功率场合,不适合应用于对输出电压的质量要求较高的场合。
本文中研究的一种将正反激电路[3]应用于传统单级Buck-Boost反激变换器,提出了一种单级无电解电容Buck-Boost正反激PFC变换器。它继承了传统电路中漏感回馈电路的优点,并且PFC级和DC/DC级均存在中间级电容进行能量的传递,变压器工作在正反激的模态,其磁芯利用率较高[6-7],此电路拓扑实现无电解电容的原理和传统拓扑一致,由于DC/DC级存在续流电感和滤波电容共同进行滤波,通过增大中间级电压纹波,增大了输出功率,其输出电压的纹波率较小。
1 工作原理
局限于中间级电容大小的影响,传统无电解电容Buck-Boost反激PFC变换器只能应用于功率很小的场合,本文中改变了变压器反激式拓扑结构,将正反激电路应用于这种PFC变换器拓扑中,提出了如图1所示的单级无电解电容Buck-Boost正反激式PFC变换器。为了简化理论分析,对电路拓扑提出以下假设:

图1 单级无电解电容Buck-Boost正反激变换器Fig.1 Single-stage electrolytic-capacitor-free Buck-Boost forward-flyback converter
(1)除了变压器存在漏感以外的其他元件均是理想的,不存在寄生参数,因此可以理解其不存在损耗,效率为100%。
(2)Vrec表示经过整流桥整流过后的电压,其表达式 Vrec=Vm|sin(ωt)|,Vm是交流输入电压的峰值,ω是电网角频率,ω=2πf。
(3)因为开关频率远大于电网的角频率,故在一个周期内可以视为电网输入电压是恒定值,即输入电容Cin的电压是不变的。
(4)假设中间级电容C1、C2和滤波电容C0足够大,即在中间级电容和滤波电容两端电压均为恒定值。
如图2所示,变换器在一个开关周期内分为4个工作模态,各个模态的关键波形如图3所示。
模态 1[t0,t1]:开关管 Q1、Q2导通,变压器工作在正激方式下,等效工作模式如图1(a)所示,此种模态下有3种回路:①电感La充电回路,该回路由Cin、VD0、La、Q1组成,在 Vrec的作用下,电感电流 iLa线性增长;②励磁电感Lb充电回路,该回路由电容C1、开关管Q1、变压器原边电感组成,中间级电容C1为原边电感充电,励磁电感Lb上的电流线性增长;③副边正激模态电路,副边二极管VD2关断,副边感应电压和电容C2的电压进行叠加共同为负载进行供电,iL0线性增长。模态对应于图3(a)所示为D1Ts阶段,D1为开关的占空比,Ts为开关周期。
模态 2[t1,t2]:开关管 Q1、Q2同时关断,该阶段下有4条回路:①电感La放电回路,该回路由La、C1、VD0、VD1组成,电感 La通过 VD0和 VD1向 C1进行充电iLa线性下降;②漏磁电感Lbk放电回路,该回路由变压器原边电感、Cin组成,漏磁能量通过二极管VD3反馈到输出端,漏电感与输入电容Cin发生谐振,iLbk呈非线性减少,在t2时刻,漏感能量放电完毕;③副边电感反激回路,该回路由副边电感、VD2、Q3、C2组成,变压器中的反激能量为 C2进行充电,反激电流iLbs下降;④续流电感L0续流回路,续流电感L0对负载进行续流,iL0线性减少。由于副边也存在漏感,漏感与C2和副边开关Q2寄生电容发生谐振作用,在关断的瞬间Q2两端出现尖端电压。
模态 3[t2,t3]:开关管 Q1、Q2继续关断,漏电感已经放电完毕,同模态2工作模式相似,电流iLa与iLbs继续下降,无论哪种先行减少到0,因为不影响整体电路的工作模态,故t3即指代两种电流最后下降到0的时刻。
模态 4[t3,t4]:开关管 Q1、Q2继续关断,并且 iLa与iLbs均已经放电结束,由于励磁电感电流逐渐降为0,在这一时期副边等效励磁电感Lbs、C2和Q2寄生发生谐振,开关管Q2上的电压将发生振荡电压,最终Q2两端的电压与Vc2大小相等。电感L0继续为负载进行续流,续流电感L0工作在CCM模态。t4时刻整个开关周期结束。

图2 各阶段等效拓扑Fig.2 Equivalent topological of stages

图3 工作模态及关键波形Fig.3 Operating modal and key waveforms
2 变换器特性分析
2.1 功率因数及占空比D1的计算
交流端输入电压设为 Vin=Vmsin(ωt);Vm为输入电压的峰值。经过整流桥后输入电压Vrec=Vm|sin(ωt)|。电路工作在DCM状态,电感La的峰值电流iLa_p为

由电路的工作模态可知,输入电流的平均值为

可知,在DCM工作模态下,输入电流与电压呈完全的正弦函数关系。
在一个工作周期内,输入功率Pin为

式中,fs为开关频率。
控制电路进行快速的电压调节,占空比可以近似为

2.2 中间级电容电压Vc1、Vc2的计算
变换器工作在正激模态时,变压器与中间级电容电压C2叠加共同为后级进行能量传递。续流电感L0上在[0,D1Ts]输入电流的平均值为

在一个工作周期Ts内变压器与中间级电容C2为负载提供的能量为

基于输入输出的功率平衡,即P0=Pin,得到
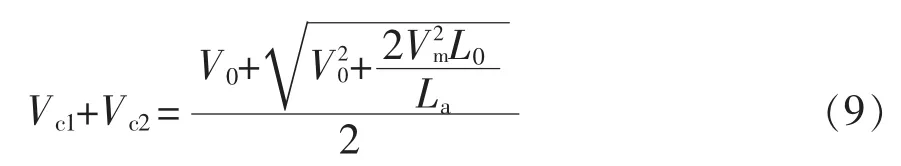
由式(9)可知:①中间级电容C1与C2上的电压之和与负载没有关系,一旦确定了输出电压V0和输入电压峰值Vm,Vc1+Vc2只和L0和La存在关系;②如果L0和La的比值确定,Vc1+Vc2是Vm的非线性函数关系。
变压器工作在励磁电流断续模态,副边的中间级电容C2与反激式变换器工作在励磁电流断续模态相同,其电压Vc2与Vc1满足的关系式为

式中,k为变压器工作在断续模式下的不连续度,取值范围为0<k≤1,k=1时,代表工作在励磁电流连续模式,k的表达式为
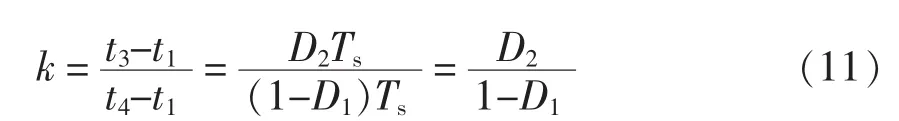
式中,D2为变压器副边反激电流下降到0时对应的占空比。则有

由式(9)和式(12)可得

根据方程式(13),电感 La=660 μH、L0/La=1.8、输入电压为220 V、输出电压为50 V时,Vc1在不同k值下与占空比D1的关系曲线如图4所示。从中可知在同一占空比下,不连续度k越小,中间级电容Vc1越小。

图4 在不同k下Vc1与D1的关系曲线Fig.4 Curves of Vc1vs D1with different values of k
输出侧等效电路如图5所示。从等效电路可知,输出侧是一个受控Buck电路,则输出电压V0的表达式为

关于K值的解释:K值的选取和前级的电感La以及变压器的励磁电感的选取以及工作模态等等都有直接的联系,这里面K值的使用旨在于理解中间级电容上的电压大小,更好的理解输出电压和中间级电容上电压之间的联系。

图5 输出侧等效电路Fig.5 Equivalent circuit of output side
由式(14)可知,输出电压V0与前级中间级电容电压Vc1成的关系,因为具有很好的宽范围输入特性,这样可以通过增大中间级电容C1的纹波来提高变换器的输出功率,并且由于副边通过续流电感和滤波电容共同进行滤波,这样可以在增加功率的条件下并不需要很大的滤波电容,续流电感的存在也使得输出的高频纹波变得很小。
3 实验结果
为了验证所提出电路的正确性,制作完成了一台30 W原理样机,如图6,该样机设计指标为:输入线电压 Vac:130~260 V,60 kHz,输出 50 V/625 mA,效率为85%,无电解电容。

图6 主电路实验样机Fig.6 Experimental prototype of main circuit
根据设计指标,结合以上的分析,本文设计的满足上述指标的驱动电路参数如下:共模电感10 mH,输入电容 0.1 μF/500 V,输入电感 La=660 μH,前级薄膜电容C1=10 μF,一次侧电感Lb=440 μH,变压器一、二次侧匝比为1,后级薄膜电容C2=10 μF,输出滤波电感L0=1.2 mH,输出滤波电容为薄膜电容 C0=20 μF,二极管均选用 MUR840G,前级开关管为IXFH11N80,后级开关管为IRFP340,控制芯片采用TL494CJ,驱动芯片采用A3120。
图7为输入220 V时输入电压电流波形,可以发现在额定功率下,输入电流iin很好地跟随了输入电压的波形,实现了功率因数校正。
图8为220 V额定功率下中间级电容C1、C2的波形,中间级电容Vc1峰值为200 V,纹波大约为80 V,Vc2峰值为150 V左右,其纹波大约为25 V。两者同相位。
图9为220 V额定功率下开关管两端电压波形,VQ1不存在由于变压器漏感而产生的峰值电压,说明漏感回馈电路很好地吸收了漏感电流。

图7 输入端电压、电流波形Fig.7 Waveforms of input voltage and input current

图8 中间级电容电压波形Fig.8 Voltage waveforms of center capacitances
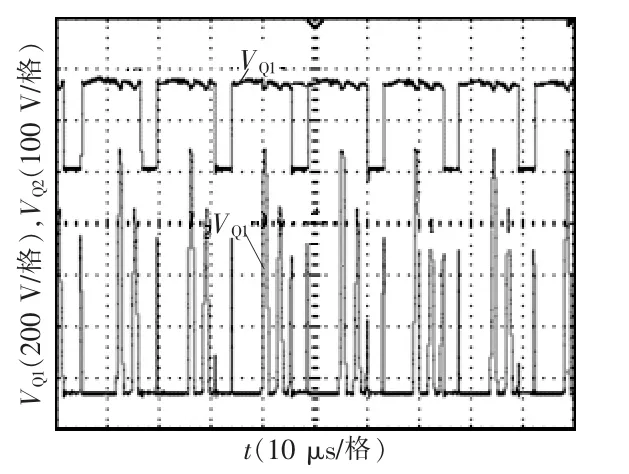
图9 开关管Q1、Q2两端电压波形Fig.9 Voltage waveforms at two terminals of switch tubes Q1and Q2
在开关管Q2关断的瞬间,由于副边漏电感的作用,瞬间Q2两端的电压上升到300 V,随后在副边反激电流的作用下很快下降至0。副边反激电流下降到0后,副边励磁电感、副边电容C2与开关管Q2发生谐振,开关管两端的电压发生振荡,由于在实际参数选择中,实验中的振荡时间过长,Q2两端的电压没有稳定至VC2之前,下个开关周期已经来到,出现如图9所示的电压波形。
图10为输出电压波形,输出电压稳定在50 V,输出电流平均值在700 mA左右,达到了预期设定值。由于存在续流电感和滤波电容的作用,其高频纹波很小,2倍频纹波峰峰值在2 V,纹波率4%,说明其控制性能良好。

图10 输出电压和输出电流波形Fig.10 Waveforms of output voltage and output current
图11给出了在额定功率下该PFC变换器输入电压、功率因数随输入电压的变化曲线。在图中可以看出,随着输入电压的增大,功率因数在逐渐的减小,效率在逐步的增大,相对于传统Buck-Boost反激试变换器,因元件数目应用的增多,并且工作功率的增大,对其效率有一定的影响,但是最低都能保证有82%的效率,且在最大输入电压下效率接近90%;PF值都能在0.95以上。

图11 效率、功率因数和输入电压的关系曲线Fig.11 Relationship curves of input voltage vs efficiency and power factor
4 结语
目前,大容量电解电容的应用已经大大影响了LED驱动照明驱动的使用寿命,成为其应用推广的阻碍。本文提出了一种无电解电容的LED驱动电路,在继承了传统驱动电路漏感能量反馈至输入端的优点,将正反激电路成功应用于DC/DC级,通过两级中间级电容与续流电感的使用,在提高输出功率的同时,输出纹波率大幅下降,磁芯利用率得到提高。
参考文献:
[1]Li Y C,Chen C L.Single-stage electrolytic-capacitors-free AC-to-DC LED driving circuit with high-power-factor[J].IEEE Trans.Ind.Electron,2012,59(2).
[2]张能,张波,丘东元.无电解电容LED驱动电路现有研究技术剖析[J].电工电能新技术,2014,33(2):44-51.Zhang Neng,Zhang Bo,Qiu Dongyuan.Analysis of cureent research technology about LED driver circuit without electrolytic capacitor[J].Advanved Technology of Electrical Engineering and Energy,2014,33(2):44-51(in Chinese).
[3]何林,曾怡达,朱仁伟,等.一种新型正-反激变换器的研究[J].电源学报,2015,13(1):87-93.He Lin,Zeng Yida,Zhu Renwei,et al.Study on a novel forward-flyback converter[J].Journal of Power Supply,2015,13(1):87-93(in Chinese).
[4]曾怡达,何林,杨岳毅,等.一种单级无电解电容LED驱动电路[J].电源学报,2014,12(3):47-51.Zeng Yida,He Lin,Yang Yueyi,et al.Study of a singlestage electrolytic-capacitor-free LED driving circuit[J].Journal of Power Supply,2014,12(3):47-51(in Chinese).
[5]Ma Hongbo,Yu Wengsong,Zheng Cong,et al.A universal-input high-power-factor PFC preregulator without electrolytic capacitor for PWM dimming LED lighting application[J].2011 IEEE Energy Conversion Congress and Exposition,2011:2288-2295.
[6]Billings K,Morey T.开关电源手册[M].3版.张占松等,译.北京:人民邮电出版社,2012.
[7]Sanjaya.精通开关电源设计[M].王志强等,译.北京:人民邮电出版社,2008.

