基于自适应下垂控制的柔性能源变换器

华磊杰 ，江 峰 ，赵 斌 ，陆 翌 ，陈 敏

（1.浙江大学电气工程学院，杭州 310027；2.国网浙江省电力公司，杭州 310007）

下垂控制最初被应用于独立交流系统中逆变器的并联控制[1]，由于其不需要通讯即可进行功率均分，具有良好的模块化和扩展性，适用于孤岛运行[2，3]。近年来随着分布式能源的大力发展，常规的并网逆变器大量接入电网。在具有下垂控制的逆变器之间加入低频通讯,通过上位机的信号传输可以很好地实现并联和均流，同时使其能够在并联情况下对并离网过程实现无缝切换，从而建立了柔性能源变换器 FEC（flexible energy converter）的概念[4-6]。该方法不仅在孤岛运行时能够对微电网提供电压支撑，在并网时可以对电网起到电压稳定作用，而且在电网故障时能够实现无缝切换。然而随着分布式能源比例的不断增加，电网结构逐渐从具有少量大功率同步发电机的集中式结构向具有大量小功率分布式能源的分散式结构变化。集中式结构中同步发电机转子存储的动能在电网负载突变时能提供短时的能量支撑，而分布式能源中的电力电子变换器往往缺乏惯性支撑。为了改善具有大量分布式能源变换器并网的电网稳定性，“虚拟同步机”的概念被提出[7-9]，随后国内外很多高校都对其进行了研究和改进[10-22]。虚拟同步机一方面模拟同步发电机特性从而引入同步发电机的稳定性问题，一方面底层由电力电子器件和相应控制实现因此兼有传统逆变器的特点。研究表明在虚拟同步机中惯性过大将使系统失稳[15，16]，因此开展了一系列对虚拟同步机振荡的研究。文献[17]提出采用有源阻尼控制策略可以抑制同步频率谐振；文献[18]研究提出保证两台虚拟同步机并联时参数相等也可以保证负载变化时输出功率不发生振荡；文献[19]用一阶滞后环节实现VSG对同步发电机的模拟可以有效抑制负荷变化时引起的系统频率振荡；文献[20]针对虚拟同步机多机系统提出一种基于粒子群算法的控制参数优化；文献[21，22]通过判断暂态时刻的不同状态来调整惯性可以减小达到稳定状态的时间并对其稳定性进行了证明，但是其系统暂态能量分析时忽略了阻尼能量。

比较下垂控制和“虚拟同步机”，其在稳态时的等效性得到了验证[23,24]，但是当输出功率指令突变时下垂控制中角频率的突变易造成系统的不稳定。对下垂控制法进行改进并和“虚拟同步机”进行了比较得到低通滤波器LPF（low pass filter）具有“虚拟同步机”中惯性的效果[25，26]，但是未对实际逆变器主动控制输出功率导致的突变情况以及暂态能量进行分析。

本文对基于下垂控制的FEC增加了惯性，通过推导得到下垂控制中加入LPF具有和同步机转动方程一样的效果并得到LPF中时间常数T与同步机惯性常数H的对应关系。同时将文献[21，22]中提出的惯性控制引入到下垂控制并针对下垂控制中的参数对暂态振荡能量进行完善分析（包括暂态动能、暂态势能以及增加了阻尼能量），对各个阶段的能量变化进行了简明清晰的公式表示。把下垂控制与同步发电机的转动方程更紧密的结合，提出当输出功率指令突变时低通滤波器进行自适应变换的下垂控制，使逆变器在暂态过程中既能够具有较大的惯性，同时可以减小功率过冲，从而更快地达到新的稳态。随后把并网前同步过程与功率指令突变过程进行分析比较，得出其相似性，并将自适应下垂控制应用于逆变器的并网同步，使其既能够保证孤岛系统的频率稳定，又能够加快同步速度。最后对并网同步和并网状态的自适应下垂控制进行了仿真，并实验验证了并网下自适应下垂控制的有效性。

1 基于自适应下垂控制的FEC

本文采用自适应下垂控制的逆变器控制框图如图1所示。首先对逆变器的输出电压和输出电流采样后进行功率计算，功率进行自适应下垂控制（本文主要关注有功控制），再经过电压和电流双环控制得到控制逆变器输出的SPWM波，最终实现控制逆变器输出的目的。

1.1 对FEC增加惯性

基于下垂控制的FEC采用低频通讯线实现与上位机的通讯[4-6]，在并、离网运行时都采用下垂控制，从而能够实现并离网的无缝切换，且在并、离网运行时都可以很好地实现负载功率均分以及系统功率平衡。但是采用传统下垂控制的FEC缺乏惯性，在输出功率指令突变时容易导致频率突变。

图1 采用自适应下垂控制的逆变器控制框图Fig.1 Control block diagram of inverter based on adaptive droop control

传统下垂法有

式中：ω为参考角速度；ω0为额定角速度（或电网角速度）；Pout为逆变器输出功率；Pref为输出功率指令；m为下垂系数。在式（1）中增加LPF，可得

对式（2）进行移项和反拉普拉斯变换，可得

式中：T为LPF的时间常数；PD为阻尼功率PD=Δω/m；Δω为逆变器输出频率与额定角速度（电网角速度）的差，Δω＝ω-ω0。

同步机的转动方程[20]为

式中：J为同步发电机的转动惯量；ωm为同步发电机的机械角速度，在极对数为1的情况下为电气角速度[28,29]；ωg为电网角速度；D为阻尼因子。

假设电网频率不变，并网条件下下垂控制中的ω0等于ωg为常量；逆变器的参考角速度ω即等效同步发电机的机械角速度ωm。将式（5）中ωg和ωm分别用ω0和ω替代，可得

对比式（4）和式（6），两者具有相似的结构。当满足

时，两者相等。在同步发电机中，J表示为

式中：H为同步机惯性常数，通常在2～10 s之间；Sbase为额定功率。根据式（7）和式（8）可得

上述推导可得，传统下垂控制加入LPF后，与同步发电机的转动方程具有相同的表达式。将所需的惯性常数代入式（9）即可得到对应LPF的时间常数T，因此对FEC的下垂控制进行改进即可使其具有同步机的惯性效果。

1.2 自适应下垂控制暂态能量分析

FEC在大惯性下动态响应变慢，当输出功率指令突变时容易造成功率过冲。然而电力电子设备的耐冲击能力远远小于同步发电机，因此本文对输出功率指令突变时变换器的暂态能量进行分析，提出一种抑制频率振荡并减小功率过冲的自适应下垂控制。

参考电机动力学中的能量函数[27]，将其用到下垂法中。将式（4）移项得

对式（10）两边乘以Δω再积分，可以得到

式中：V为总暂态能量；Ek为暂态动能；EP为暂态势能；ED为阻尼能量。

图2是下垂控制中模仿同步发电机的功角曲线，图3是功角曲线下功率波动时的功率与相位差在阻尼情况下的振荡波形。因为下垂控制中加入了LPF模拟惯量，所以当输出功率指令变化时实际输出功率必然存在振荡。当功率发生波动时，如图2中输出功率指令从P0变为Pref时，逆变器输出点将会沿着功角曲线从点a滑动到c，再从c滑动到a（若考虑阻尼，则无法再次达到最高点a）。图3中的曲线1-2-3对应图2中从a到c的（Pout+PD）曲线，其中 Δδ=δ-δ0。

图2 逆变器输出的功角曲线Fig.2 Power-angle curve of inverter

图3 阻尼情况下功率与相位差的振荡波形Fig.3 Oscillations waveforms of power and phase difference with damping

在式（4）中，当 Pref、Pout和 PD为确定值，m 为常数时，T越大则频率变化越慢但达到稳态时间越长；相反，T越小则达到稳态时间变短但是频率变化越快。为了实现小的频率变化且快速达到稳态，本文提出带自适应LPF的下垂控制。

设area 1-2-7表示点1、点2、点7围成的面积，其他类同。图3中当振荡1点开始时，可以看出此时 Δω=0，Δδ最大。由式（11）可以得到点 1时的暂态能量为在振荡从点1到点2过程中，大Tbig能够模拟大惯性去抑制角速度偏离额定值，此过程中有

在点 2 处，Ek=area 1-2-7，达到最大（此时|Δω|达到最大）。此时将T从Tbig变成Tsmall，Ek变化为

式中：Ek2-为T变换前暂态能量；Ek2+为T变换后暂态能量。Ep和ED在这一瞬间保持不变，因此总暂态能量V减小。从点2到点3的过程类似，则有

由于总暂态能量V在点2减小，所以最低点3比不改变Tbig时离Pref更近（能量过冲减小），则area 2-3-8的面积从左边等式变成右边等式，即

在点 3处，Ek=0（Δω=0），因此在该点将 T 从 Tsmall变成Tbig不影响各个暂态能量。3-4-5的过程如1-2-3，变化T并且不断循环，直到Ek+Ep=0（即总暂态能量都变成阻尼功率）。由于在变化过程中总暂态能量V不断减小，因此系统再次达到稳定所需时间也变短。

表1 每个振荡周期LPF时间常数T的变化Tab.1 Variation of LPF time constant T during each cycle of oscillations

在每个振荡周期内，LPF中的时间常数值T改变4次，其变化规律如表1所示。

通过分析不同时刻变换器暂态能量的变化过程，对调整LPF时间常数T所起的作用进行分析，验证了所提自适应下垂控制在保持所需大惯性情况下能够减小功率过冲，以及缩短再次达到稳定状态的时间。考虑到实际测量环节及执行过程中的误差，可对Δω设定为一个小阈值，避免T的振荡（本文中阈值设为0）。

1.3 自适应下垂的并网同步分析

孤岛运行时逆变器Pref为0，则运行公式为

当并网同步时，逆变器控制方程变为

式中：θ为逆变器输出电压相位角；θg为电网相位角；Pmax为图2功角曲线中的功率最大值。

在并网同步时，假设本地负载不变，因此Pout为常数（若本地负载变化，Pout-Pref仍不影响）。与并网时相反，此时通过调节逆变器角频率，使Pref在功角曲线上向Pout滑动，使孤岛母线电压与电网电压相位差为0（并网时，Pout向Pref滑动，使相位差达到满足功角曲线的点）。将并网前同步与并网时刻输出功率跟随进行对比，结果如表2所示。

表2 并网前同步过程与并网功率跟随对比Tab.2 Comparing synchronous before grid-connected and power following in grid-connected

由表2可知，并网前同步与并网时的功率跟随除了不变量和暂态过程调节量互换，具有相同的控制方程表达式，目标都是将相位差调至一个常量。因此第1.2节中的暂态能量分析也完全适用于并网前同步分析，只是同步中调节的功率Pref为虚拟功率，而并网调节的Pout是实际逆变器输出功率，但对控制而言并不影响。因此将自适应下垂控制应用于并网前同步，即能够在并网时模拟转子的转动惯性，防止孤岛电网频率突变而导致系统不稳定，又能够加快同步速度。

2 仿真验证

为验证所提的自适应下垂控制在FEC中的可行性，本文在PLECS中搭建了图4所示的仿真拓扑。仿真中主要参数如表3所示，其中下垂系数的取值参考文献[5]。

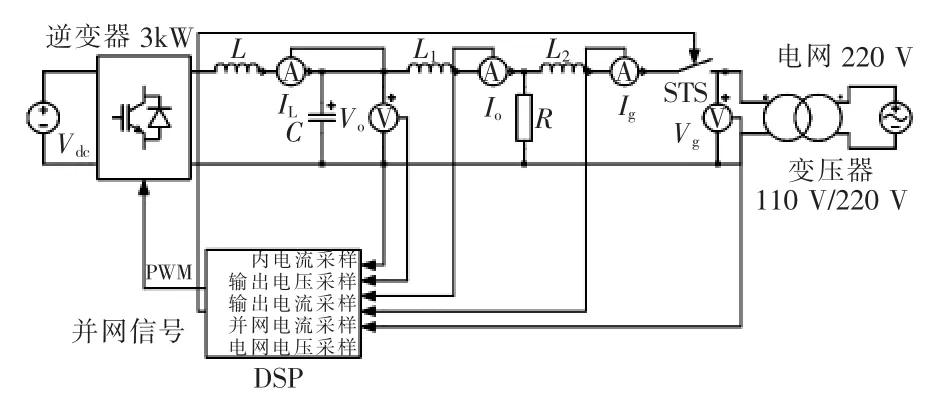
图4 仿真电路原理Fig.4 Principle of simulation circuit

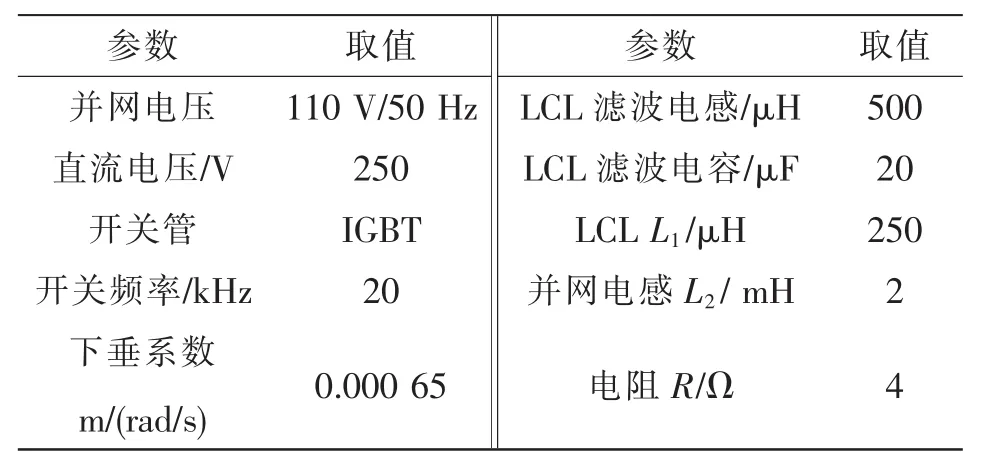
表3 仿真与实验主要参数Tab.3 Main parameters in simulation and experiment

图5为采用固定LFP的下垂控制与采用自适应LPF的下垂控制仿真波形比较，其中根据式（7），Tbig=0.025 s（H=10 s），Tsmall=0.005 s（H=2 s）。在 t=5 s时，系统的输出功率指令从3 kW减小为1.5 kW；t=8 s时，系统的输出功率指令从1.5 kW减小为0.5 kW；t=11 s时，系统的输出功率指令从0.5 kW增大为2 kW。图5可见，在输出功率指令突变时，输出频率都有相同的缓慢变化过程，体现了两者相同的惯性。然而当频率降到最低点以后，图5（b）中的频率较快恢复到额定值50 Hz，而图5（a）中的频率仍然缓慢地恢复，可见，图5（a）中功率下降波动大于图5（b）。同时，采用自适应LPF的下垂控制能够更快地再次达到稳定状态。

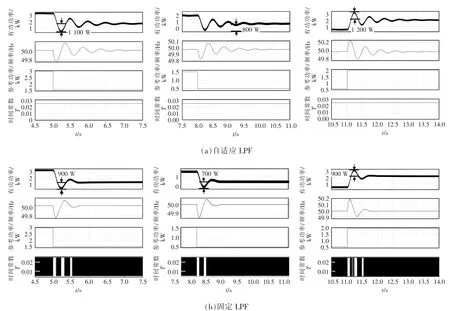
图5 固定LPF（T=0.025 s）与自适应LPF（Tbig=0.025 s and Tsmall=0.005 s）的下垂控制仿真比较Fig.5 Comparison of simulation between the droop control with fixed LPF(T=0.025 s)and that with alternating LPF(Tbig=0.025 s,Tsmall=0.005 s)

图6为自适应LPF的下垂同步和固定LPF的下垂同步（相位差范围在[-π，π]之间），仿真比较，其中，图6（a）中同步前逆变器相位落后于电网相位，图6（b）中同步前逆变器相位领先于电网相位。由图可见，采用自适应LPF的下垂在同步开始时能够保持大惯性，防止频率突变，同时能够较快地完成同步过程。

图6 固定LPF的下垂与自适应LPF的下垂并网前同步仿真比较Fig.6 Comparison synchronous of the droop with the fixed LPF and the droop with alternating LPF before grid-connected

综上所述，采用自适应LPF的下垂控制在输出功率指令突变时具有抑制频率波动所需要的大惯性环节（时间常数都是0.025 s），而且能够更快地再次达到稳定状态，具有更小的功率过冲；在并网前同步过程中也能够在保持大惯性情况下快速完成同步过程。同时并网前后控制方程实现了统一，有利于后期并网过程的研究。

3 实验验证

为了验证理论分析和仿真的准确性，搭建了如图7所示的实验平台。实验平台与仿真平台参数设置一致，由1台全桥LCL单相逆变器、工频110 V/220 V变压器、带labview的上位机（通过CAN通讯来控制逆变器并离网切换以及输出功率控制）、示波器及各种配件组成。

图8和图9是用8通道示波器（TELEDYNE LECROY HD 4096）测试得到，自上而下依次是：逆变器稳态输出电压电流、暂态输出电压电流、输出有功功率以及输出波形的频率。图8是固定LPF（T=0.025 s）条件下不同输出功率指令切载时的输出波形；图9是自适应LPF（Tbig=0.025 s and Tsmall=0.005 s）条件下不同输出功率指令切载时的输出波形。

图7 实验平台Fig.7 Experiment platform

图8 固定LPF（T=0.025 s）下逆变器切载波形Fig.8 Waveform of inverter during power switching with fixed LPF（T=0.025 s）

由图9和图8可见，在稳态时自适应下垂控制和固定LPF的下垂控制的输出电压和电流都具有很好的波形，可见自适应LPF不影响稳定状态。在暂态过程中，由于无功输出的波动，电压电流有一定相位差。比较图8和图9的角频率波动，两者在参考功率突变时都能够平滑过渡，体现了惯性环节。根据图9中的标识可知自适应下垂控制的功率波动在两次功率指令突变时都偏离额定值更小（小了近100 W），而且更快地再次达到稳定状态（快了近1 s）。

图9 自适应LPF（Tbig=0.025 s和Tsmall=0.005 s）下逆变器切载波形Fig.9 Waveform of inverter during power switching with the alternating LPF（Tbig=0.025 s和 Tsmall=0.005 s）

4 结语

本文对基于下垂控制的FEC通过增加LPF增加了其惯性特性，同时针对其大惯性下动态响应变慢而提出了自适应下垂控制。两个不同时间常数T的LPF在输出功率指令突变后进行自适应变化：当暂态势能转变为暂态动能和阻尼功率时，使用大的时间常数T来抑制角速度的改变；当暂态动能转变为暂态势能和阻尼功率时，使用小的时间常数T来加快角速度回归标准值。同时将该方法应用于并网前同步，不仅改善了并网稳定性和快速性，又实现了并网前后控制方程的统一性。提出的方法在仿真和实验中得到验证，为解决FEC输出功率指令突变时即需要保持大惯性的同时又要具有快速响应的矛盾提供了解决思路，增加了电力电子变换器对电网的友好性和可靠性。本文虽然对并网前后控制方程的统一性进行了分析，但是对并网过程还欠缺理论分析和实验验证，有待进一步深入研究。

参考文献：

[1]Chandorkar M C,Divan D M,Adapa R.Control of parallel connected inverters in standalone AC supply systems[J].IEEE Transactions on Industry Applications,1993,29（1）:136-143.

[2]De Brabandere K,Bolsens B,Van d K J,et al.A voltage and frequency droop control method for parallel inverters[J].IEEE Transactions on Power Electronics,2007,22（4）:1107-1115.

[3]Wallace K,Mantov G.Wireless load sharing of single phase telecom inverters[C]//The 21st International Telecommunication Energy Conference,1999.INTELEC'99.Copenhagen,Denmarlc,1999:7.

[4]Gao Mingzhi,Zhang Canhui,Qiu Maohang,et al.An accurate power-sharing control method based on circulatingcurrent power model for voltage-source-inverter parallel system[C]//2015 IEEE Applied Power Electronics Conference and Exposition.Charlotte,NC,USA，2015:1815-1821.

[5]Gao Mingzhi,Zhang Yuru,Jin Cheng,et al.An improved droop control method for parallel operation of distributed generations in microgrid[C]//2013 Twenty-Eight Annual IEEE Ap-plied Power Electronics Conference and Exposition.Long Beach,CA,USA,2013:3016-3020.

[6] Jin Cheng,Gao Mingzhi,Lü Xiaofeng,et al.A seamless transfer strategy of islanded and grid-connected mode switching for microgrid based on droop control[C]//2012 IEEE Energy Conversion Congress and Exposition.Raleigh,NC,USA,2012:969-973.

[7]Beck H P,Hesse R.Virtual synchronous machine[C]//International Conference on Electrical Power Quality and U-tilisation.IEEE,2007:1-6.

[8]Driesen J,Visscher K.Virtual synchronous generators[C]//2018 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century.Pittsburgh,PA,USA,2008:1-3.

[9]Loix T,Breucker S D,Vanassche P,et al.Layout and performance of the power electronic converter platform for the VSYNC project[C]//2009 IEEE Bucharest Power Tech,Bucharest,Romania,2009:1-8.

[10]石荣亮,张兴,徐海珍,等.基于虚拟同步发电机的微网运行模式无缝切换控制策略[J].电力系统自动化,2016,40（10）:16-23.Shi Rongliang,Zhang Xing,Xu Haizhen,et al.Seamless switching control strategy for microgrid operation modes based on virtual synchronous generator[J].Automation of Electric Power Systems,2016,40（10）:16-23（in Chinese）.

[11]孟建辉,王毅,石新春,等.基于虚拟同步发电机的分布式逆变电源控制策略及参数分析[J].电工技术学报,2014,29（12）:1-10.Meng Jianhui,Wang Yi,Shi Xinchun,et al.Control strategy and parameter analysis of distributed inverters based on VSG[J].Transactions of China Electrotechnical Society,2014,29（12）:1-10（in Chinese）.

[12]吴恒,阮新波,杨东升,等.虚拟同步发电机功率环的建模与参数设计[J].中国电机工程学报,2015,35（24）:6508-6518.Wu Heng,Ruan Xinbo,Yang Dongsheng,et al.Modeling of the power loop and parameter design of virtual synchronous generators[J].Proceedings of the CSEE,2015,35（24）:6508-6518（in Chinese）.

[13]佘洪伟,刘进军,刘增,等.一种改进型虚拟同步发电机控制方法研究[J].电力电子技术,2015,49（11）:63-65.She Hongwei,Liu Jinjun,Liu Zeng,et al.Research on an improved control method of virtual synchronous generator[J].Power Electronics,2015,49（11）:63-65（in Chinese）.

[14]王金华,王宇翔,顾云杰,等.基于虚拟同步发电机控制的并网变流器同步频率谐振机理研究[J].电源学报,2016,14（2）:17-23.Wang Jinhua,Wang Yuxiang,Gu Yunjie,et al.Synchronous frequency resonance in grid-connected VSCs with virtual synchronous generator technology[J].Journal of Power Supply,2016,14（2）:17-23（in Chinese）.

[15]颜湘武,刘正男,张波,等.具有同步发电机特性的并联逆变器小信号稳定性分析[J].电网技术,2016,40（3）:910-917.Yan Xiangwu,Liu Zhengnan,Zhang Bo,et al.Small-signal stability analysis of parallel inverters with synchronous generator characteristics[J].Power System Technology,2016,40（3）:910-917（in Chinese）.

[16]Liu Jia,Miura Y,Ise T.Comparison of dynamic characteristics between virtual synchronous generator and droop control in inverter-based distributed generators[J].IEEE Transactions on Power Electronics,2015,31（5）:3600-3611.

[17]李武华,王金华,杨贺雅,等.虚拟同步发电机的功率动态耦合机理及同步频率谐振抑制策略[J].中国电机工程学报,2017,37（2）:381-390.Li Wuhua,Wang Jinhua,Yang Heya,et al.Power dynamic coupling mechanism and resonance suppression of synchronous frequency for virtual synchronous generators[J].Proceedings of the CSEE,2017,37（2）:381-390（in Chinese）.

[18]Liu Jia,Miura Y,Bevrani H,et al.Enhanced virtual synchronous generator control for parallel inverters in microgrids[J].IEEE Transactions on Smart Grid,2017,8 （5）:2268-2277.

[19]Hirase Y,Noro O,Sugimoto K,et al.Effects of suppressing frequency fluctuations by parallel operation of virtual synchronous generator in microgrids[C].2015 IEEE Energy Conversion Congress&Exposition,Montreal,QC,Canada 2015:3694-3701.

[20]Alipoor J,Miura Y,Ise T.Stability assessment and optimization methods for microgrid with multiple VSG units[J].IEEE Transactions on Smart Grid,2016,99:1-10.

[21]Alipoor J,Miura Y,Ise T.Distributed generation grid integration using virtual synchronous generator with adoptive virtual inertia[C]//Energy Conversion Congress and Exposition.IEEE,2013:4546-4552.

[22]Alipoor J,Miura Y,Ise T.Power system stabilization using virtual synchronous generator with alternating moment of inertia[J].IEEE Journal of Emerging&Selected Topics in Power Electronics,2015,3（2）:451-458.

[23]D'Arco S,Suul J A.Equivalence of virtual synchronous machines and frequency-droops for converter-based microgrids[J].IEEE Transactions on Smart Grid,2014,5 （1）:394-395.

[24]D'Arco S,Suul J A.Virtual synchronous machines—Classification of implementations and analysis of equivalence to droop controllers for microgrids[C]//Powertech.IEEE,2013:1-7.

[25]Liu Jia,Miura Y,Ise T.Comparison of dynamic characteristics between virtual synchronous generator and droop control in inverter-based distributed generators[J].IEEE Transactions on Power Electronics,2015,31（5）:3600-3611.

[26]Guan Minyuan,Pan Wulue,Zhang Jing,et al.Synchronous generator emulation control strategy for voltage source converter（VSC） stations[J].IEEE Transactions on Power Systems,2015,30（6）:3093-3101.

[27]Machowski J,Bialek J W,Bumby J R.Power system dynamics:stability and control[M].2nd ed.New Jersey:Wiley,2008:128-227.

[28]石荣亮,张兴,徐海珍,等.基于虚拟同步发电机的微网运行模式无缝切换控制策略[J].电力系统自动化,2016,40（10）:16-23.Shi Rongliang,Zhang Xing,Xu Haizhen,et al.Seamless switching control strategy for microgrid operation modes based on virtual synchronous generator[J].Automation of Electric Power Systems,2016,40（10）:16-23（in Chinese）.

[29]吕志鹏,盛万兴,钟庆昌,等.虚拟同步发电机及其在微电网中的应用[J].中国电机工程学报,2014,34（16）:2591-2603.Lyu Zhipeng,Sheng Wanxing,Zhong Qingchang,et al.Virtual synchronous generator and its applications in micro-grid generator[J].Proceedings of the CSEE,2014,34（16）:2591-2603（in Chinese）.