云计算下基于改进遗传算法的聚类融合算法

徐占洋，郑克长

(南京信息工程大学 计算机与软件学院，南京 210044)(*通信作者电子邮箱983119701@qq.com)

0　引言

随着数据量的日益增长，要处理的数据信息规模也随之增大，传统模式的大数据挖掘处理技术已经无法满足现在对于算法效率和准确度的要求。云计算为大数据的挖掘与处理提供了便利的服务，而Hadoop则为大数据处理技术提供了很好的解决方案。对于无监督数据聚类，不同的数据集需要选择不同的、合适的聚类算法，这无疑增加了工作量与工作难度。为了解决上述问题，Strehl等[1]提出了合并独立聚类算法的思想，这就是聚类融合的由来。相比单一聚类算法，聚类融合具有以下优点：

1)鲁棒性。许多研究实验表明，聚类融合在不同领域和不同数据集上的表现都优于独立的聚类算法。也就是说，聚类融合的算法性能，即最终划分的准确度优于单一聚类算法。

2)稳定性。单一聚类算法大多受噪声数据、异常值、数据分布等影响，而聚类融合对于这些因素则不敏感。

3)可并行性和可扩展性。并不是每个聚类算法都可以并行，但聚类融合可以并行；同时，聚类融合可以从多个分布式数据源上集成基聚类。

遗传算法(Genetic Algorithm, GA)[2]是受自然选择过程启发设计的一种进化算法，它通常依靠交叉、变异和选择等操作优化和搜索问题。在实际应用中，遗传算法经常被用来解决全局优化问题。在处理大量的多维数据集时，时间和空间的高复杂度是串行聚类融合算法的一个不足之处。本文主要从以下两个方面设计实现云计算下基于改进遗传算法的聚类融合算法(Clustering Ensemble algorithm based on Improved Genetic Algorithm, CEIGA)：

1)聚类融合要求基聚类具有多样性，基于此本文设计了新的选择算子用于遗传算法。同时，本文将改进后的遗传算法作为聚类融合的一致性集成函数，合并基聚类生成最终聚类结果，从而提高一般聚类融合算法的性能，降低算法的空间复杂度。

2)本文采用Hadoop分布式框架实现基于改进遗传算法的并行聚类融合算法。MapReduce编程模型是Hadoop框架中的一个核心部分，它能够提高基于改进遗传算法的并行聚类融合算法的计算效率，降低算法的时间复杂度。

1　相关工作

由于不同的聚类算法在同一个数据集上会得到不同的聚类结果，Strehl等[1]提出了聚类融合这一概念，并对其进行了定义：对同一数据集进行聚类得到多个有差别的基聚类划分，再将其进行合并以得到一个统一的改进的共识划分，并且不使用数据集原有的属性特征。聚类融合的出现在数据挖掘领域也掀起了研究热潮。近年来,学者们从不同方面进行探索，如基聚类的生成机制(同一种算法不同参数、不同算法、不同数据子集、不同特征子集等)[1,3-5]，一致性集成函数(投票法、基于矩阵的方法、基于图的方法等)[1,6-9]，基聚类的评估与选择(聚类评价函数和成员选择等)[9-10]和聚类融合的应用(图像视频识别、医学诊断、入侵检测等)[8,11-12]。

遗传算法是由Turing[2]根据生物学的优胜劣汰、适者生存进化机制发展而来的用于解决多目标优化问题的方案，目前已被应用于组合优化、机器学习和人工智能等领域。文献[13-15]将遗传算法用于聚类融合，并将基聚类划分作为目标，进行优化得到全局最优的共识划分。遗传算法虽然可以有效地解决聚类融合中的全局优化问题，但是如何构造简单有效的编码方式,如何选择合适的适应度函数,如何设计恰当的选择、交叉和变异算子等是改进基于遗传算法的聚类融合算法的关键。

随着时代的发展，数据量越来越大，传统的数据挖掘算法执行起来费时耗力。Hadoop平台上的MapReduce框架经常用于解决大数据集的分布式存储的并行计算问题[16]。一个MapReduce程序由一个map函数进行过滤和排序操作，一个reduce函数进行汇总操作。吴晓璇等[17]将数据空间中的分形维数用于聚类融合，同时在云计算环境下实现了其并行化；Benmounah等[18]提出了一个聚类融合并行分布式系统用于医疗疾病的诊断。

本文针对无监督聚类缺少先验信息以及聚类融合要求基聚类具有高准确性的问题，提出了基于改进遗传算法的聚类融合算法(CEIGA)。针对聚类融合算法时间复杂度高的问题，利用Hadoop设计实现了基于改进遗传算法的并行聚类融合算法(Parallel Clustering Ensemble algorithm based on Improved Genetic Algorithm, PCEIGA)。

2　基于改进遗传算法的聚类融合算法

2.1　基聚类生成机制

本文选择K-Means算法作为基聚类生成机制的主要算法，它是数据挖掘领域非常流行的一种聚类方法。给定一个数据集X={x1,x2,…,xn}，数据集中的每条数据都有d个属性，K-Means算法的目标是把数据集中的n个对象划分成k(k≤n)个簇同时使得簇内平方和最小、簇间平方和最大。

首先，K-Means算法会从原始数据集中随机选择k个数据作为初始簇中心；接着根据欧几里得公式计算每个数据到当前k个簇中心的距离，并根据计算得到的欧几里得距离将每个数据分配到离它最近的簇中心所在的簇。由于这一步操作会导致簇的分布发生变化，进而引起簇中心变化，因此，需要重新计算簇中心。簇中心的计算公式如下所示：

(1)

其中|Ci|是簇Ci内数据的数量。最后，计算出新的簇中心后，判断前后两次簇中心是否变化，如果没有变化，则K-Means算法停止；否则继续迭代。重复上述K-Means算法m次，就会得到关于原始数据集X的m次聚类划分，即m个基聚类。

2.2　基聚类簇标签转化

在采用遗传算法得到最终结果之前，必须解决基聚类的簇标签不一致问题。对于聚类划分{1,1,1,2,2,3,3,3}和{2,2,2,3,3,1,1,1}，虽然它们的表达方式不一样，但是表示的却是同一个划分。聚类融合的基聚类之间必须通过匹配建立相互的对应关系。

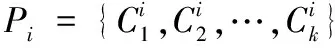
2.3　改进遗传算法

传统的聚类融合算法一般采用基于相似性矩阵的聚类算法作为一致性集成函数，但是一般的聚类算法容易陷入局部最优，同时在算法应用前需要创建关于数据或基聚类的相似性矩阵，空间和时间复杂度高。针对上述问题，本文利用改进的遗传算法作为一致性集成函数。遗传算法作为一致性集成函数的优点主要有：1)遗传算法通过进化迭代地寻找全局最优解；2)通过改进遗传算法的选择算子，选择合适的染色体进行交叉和变异操作，能使基聚类满足多样性和准确性；3)遗传算法的可并行特点是其作为一致性集成函数的重要因素之一。

遗传算法主要包括基因编码、适应度函数、选择算子、交叉和变异操作和精英策略五部分。

2.3.1基因编码

本文采用字符串编码策略。每一个基聚类会编码成一个整数字符串，其中字符串中的每一个整数表示的是当前位置的数据所被分到的簇的标签。例如，对于有5个数据的数据集，染色体(12221)表示的数据的划分是{{x1,x5},{x2,x3,x4}}。

2.3.2适应度函数

聚类融合的目标是找到一个划分使得簇内数据的相似性较高，而簇与簇之间的数据相似性较低。基于上述目标，本文提出使用平均簇内适应度和平均簇间适应度的差值表示每条染色体的适应度:

(2)

式(3)和式(4)分别计算了簇Ck的簇内适应度和Ca与Cb的簇间适应度:

(3)

(4)

其中：coij是数据xi和xj在所有划分中一起出现的频率，|Ck|是第k个簇的数据的数量，|P|是基聚类P中的簇的数量。

2.3.3选择算子

选择算子用于选择进行交叉和变异的个体。一般遗传算法采用轮盘赌作为选择算子，但是轮盘赌根据适应度随机选择染色体进行交叉变异操作，具有不确定性。针对轮盘赌的不确定性，本文根据聚类融合对于基聚类多样性的要求提出使用最多重叠数量作为选择算子。其主要思想是：对于两个基聚类，如果两者重叠元素越多，则选中进行交叉变异操作的概率越大；反之，重叠元素越少，选中进行交叉变异操作的概率越小。聚类融合对于基聚类生成机制产生的基聚类的要求是多样性和准确性，即基聚类之间互相不同且准确度高。本文提出的选择算子根据基聚类之间的重叠元素数量选择出重叠元素最多的两个基聚类进行交叉操作，生成不同的后代染色体，满足了聚类融合的多样性；选出上述两个基聚类中的适应度低的基聚类进行变异操作，满足了聚类融合的准确性。

图1　选择算子运算实例Fig. 1　Example of selecting operator

2.3.4交叉和变异操作

通过选择算子选择出用于交叉的染色体子集后，接下来会对选中的两个染色体进行交叉操作。由于种群中的每个染色体所表示的划分的簇的个数都相同，本文选用单点交叉的方法。单点交叉是在两个父母染色体的基因上随机选择一个位置点i，从位置点i以后的基因进行交换产生两个后代染色体，并加入当前种群中。

通过选择算子选择出染色体子集后，会从中选择适应度较低的一个染色体进行变异操作。在要变异的染色体上，随机选择一个位置点i突变为：

其中d(xi,Cj)是数据xi到簇Cj的欧几里得距离。

2.3.5精英策略

精英策略用于从当前种群及其交叉变异产生的后代中选择优良染色体生成下一代种群。过高的交叉率可能导致遗传算法过早收敛，如果不采用精英选择，那么变异率过高会导致好的解决方案的丢失。本文所使用的精英策略是在适应度函数(详见式(2))的基础上，选择前m个适应度高的染色体作为下一代种群进行下一步操作。

2.4　CEIGA

CEIGA主要包括三部分：1)采用不同初始中心的K-Means算法生成m个不同的基聚类；2)以其中一个基聚类作为基准基聚类，将其他基聚类与其建立对应关系，解决簇标签不一致问题；3)将解决标签不一致问题后的基聚类进行基因编码，作为改进遗传算法的初始种群输入，并且利用改进遗传算法的选择算子选择染色体进行交叉和变异保证基聚类的多样性和准确性，进而得到最优的解决方案，即聚类融合对于数据集的最终划分。其伪代码如算法1所示。

算法1CEIGA。

输入有n个数据的数据集X，基聚类数量m，最大进化次数tmax，交叉变异率α。

输出关于数据集X的划分。

1)运行K-Means算法m次生成m个基聚类；

2)解决m个基聚类的标签不一致问题。

3)根据字符串组编码策略对基聚类进行基因编码，得到初始种群并设置当前种群代数t=1。

4)计算每个染色体子集的重叠元素，选出m×α个染色体子集。

5)将步骤4)选择的染色体子集进行交叉操作得到染色体后代，加入当前种群。

6)根据式(2)计算当前种群中每个染色体的适应度值。

7)将步骤4)选择的每个染色体子集中适应度低的染色体进行变异操作得到后代，计算其适应度值并加入当前种群。

8)从当前种群中选择适应度最高的m条染色体生成下一代种群，t=t+1。

9)判断t是否等于tmax，如果满足，则选择当前种群中适应度值最高的染色体输出,否则返回步骤4)。

3　基于改进遗传算法的并行聚类融合算法

纵观大数据领域的发展可知，当前的大数据处理一直在向着近似于传统数据库体验的方向发展。云计算及其Hadoop平台的产生使得普通机器能够建立稳定的处理TB级数据的集群，从而实现并行计算。Hadoop平台上的MapReduce编程模型是并行、分布式计算的发展。MapReduce采用“分而治之”的思想，把对大规模数据集的操作派发给一个主节点管理的各分节点共同完成，然后在主节点上整合分节点的结果得到最终结果。MapReduce就是任务的分解与结果的汇总,这两个阶段分别由map函数和reduce函数完成：map函数负责把一个大型任务分解成若干个小任务，而reduce函数则负责把每个小任务的结果汇总起来。基于改进遗传算法的聚类融合算法通过改进的遗传算法对基聚类进化得到比单一聚类算法结果更准确的聚类划分,这一思想符合云计算环境下MapReduce“分而治之”的思想，因此，在基于改进遗传算法的聚类融合算法基础上，本文利用MapReduce模型设计了云计算下基于改进遗传算法的聚类融合算法(PCEIGA)。如何在云计算环境下利用MapReduce模型实现PCEIGA的并行聚类、提高算法聚类结果的准确性是本文的研究重点。

图2是PCEIGA在Hadoop平台上并行实现的框架图，主要包括两个MapReduce过程：基聚类的并行和改进遗传算法的并行。本文第一个MapReduce过程完成基聚类的生成。首先，每个节点上的map()函数将原始数据集复制到该节点上，使得每个节点上都有一份数据，然后reduce()函数对节点上的数据集进行K-Means聚类得到基聚类。在本文中有m个节点并行地执行此过程，产生m个基聚类P={P1,P2,…,Pm}；接下来，随机选择一个基聚类作为基准基聚类对其他基聚类标签转化，使得m个基聚类簇标签对应；然后将标签转化后的m个基聚类进行基因编码，产生初始种群，作为第二个MapReduce过程的输入。第二个MapReduce过程主要完成改进遗传算法的并行。首先，对基因编码得到的种群进行数据分片，分配给s个节点；然后，节点上的map()函数会读取数据获得染色体相关信息，计算每条染色体的适应度值，输出〈key(染色体id),value(适应度值)〉对。为了提高算法效率，本文在第二个MapReduce过程中加入了Combine操作。Combine的作用是对Mapper2的输出数据进行处理，降低〈key,value〉对的数量，减少节点之间要传输的数据，减少网络流量，从而达到降低节点通信的目的。第二个MapReduce过程的combine()函数根据选择算子和适应度值将染色体分为保留、交叉和变异三类，每个reduce()函数在收到关于染色体的信息后会根据相关信息对染色体进行相应的保留、交叉或变异操作后输出〈key(染色体id),value(适应度值)〉对。将reduce()函数的〈key(染色体id),value(适应度值)〉对合并形成下一代种群，如此迭代重复直至满足最大进化次数后停止，选择当前种群中适应度最高的染色体作为最终聚类结果输出。

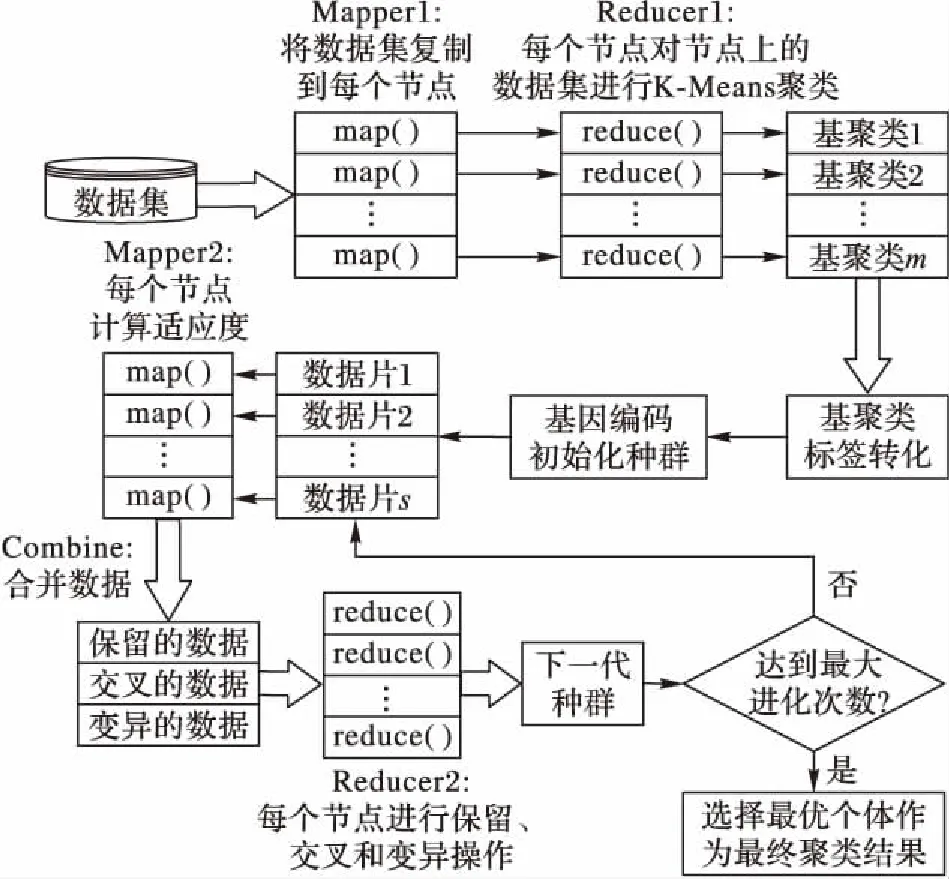
图2　云计算下PCEIGA框架Fig. 2　Framework of PCEIGA algorithm in cloud computing

4　实验与分析

本文实验的Hadoop平台是自行搭建的，采用完全分布式模式。在Windows 7(64位)操作系统上，用VritualBox软件创建6台虚拟机搭建Hadoop平台，其中1台虚拟机作为MasterNode(JobTracker)节点用于维护和管理集群中各节点，其余5台作为DataNode(TaskTracker)节点用于存储数据。各节点通过定义主机名与IP地址之间的对应关系，配置SSH(Secure Shell)，实现相互通信。节点的硬件环境是AMD FX- 6300 CPU 3.50 GHz，4.00 GB内存，200 GB硬盘，每个节点装有Ubuntu- 14.04.4-desktop-amd64操作系统，其中Hadoop版本为hadoop- 2.6.0 binary，Java版本为Java- 1.7.0_101，Eclipse版本为Juno Service Release 2。

实验数据选取的是6个常用UCI数据集，详细信息如表1所示。本文选取了不同数量大小的数据集以测试数据集大小对CEIGA和PCEIGA的影响。UCI数据集有数据的真实划分信息可以利用，但本文只将数据集的真实划分信息用于最后算法性能分析，算法本身并没有使用到这些信息。

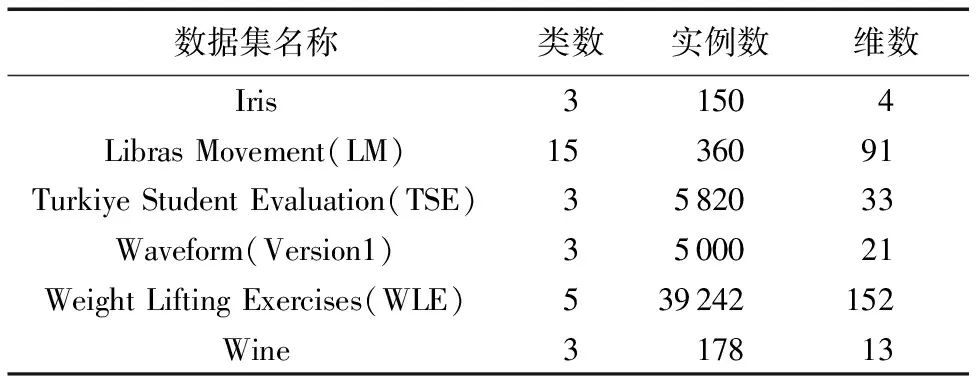
表1　实验中使用的UCI数据集Tab. 1　UCI datasets used in experiment

为了对算法的聚类结果进行有效评价，计算算法的最终结果与数据集真实划分之间的ARI(Adjusted Rand Index)值来评价算法性能。ARI的计算公式如下：

ARI(A,B)=

(5)

其中：nij是划分A的第i个簇和划分B的第j个簇的重叠元素的个数，ai是划分A的第i个簇内元素的个数，bj是划分B的第j个簇内元素的个数，n是数据集的数据个数。ARI值越大表示划分A和B的相似性越高。

4.1　CEIGA性能分析

选择与CEIGA进行对比的先进聚类融合算法包括：文献[19]的基于投票法的聚类融合(Clustering Ensemble based on Voting, CEV)、基于CSPA的聚类融合(Clustering Ensemble based on Cluster-based Similarity Partitioning Algorithm, CECSPA)、基于平均链的聚类融合(Clustering Ensemble based on Average Linkage, CEAL)和文献[20]中的基于Dempster-Shafer证据理论的聚类融合(Clustering Ensemble based on Dempster-Shafer, CEDS)。图3记录了上述算法的结果与数据集真实划分的ARI值。

图3　五种算法的ARI值对比Fig. 3　ARI value comparison of five algorithms

从图3可以看出，五个算法中表现最好的是CEIGA：在Iris、TSE、Waveform和WLE数据集上，CEIGA明显优于其他四个先进聚类融合算法；在LM和Wine数据集上，CEIGA以微弱优势胜出CEDS算法。五个算法中表现最差的是CEV算法；CECSPA和CEAL表现旗鼓相当；CEDS算法表现最不稳定，在Iris、LM、WLE和Wine数据集上表现极好，但在TSE和Waveform数据集上表现较差。分析产生上述现象主要是因为作为基聚类生成机制的K-Means算法极易陷入局部最优，故而生成的基聚类大部分会受这一现象影响而产生局部较优的结果，因此在使用投票法、CSPA、平均链凝聚层次聚类和Dempster-Shafer证据理论作为一致性集成函数时，得到的最终聚类结果是局部最优的结果。本文提出的CEIGA使用改进遗传算法作为共识函数，通过交叉和变异操作对基聚类进化得到适应度值高(簇内更近和簇间更远)的基聚类从而达到全局最优、避免局部最优。这也是CEIGA明显优于其他四个先进聚类融合算法的主要原因。

4.2　PCEIGA性能分析

为了比较云计算下PCEIGA的性能，将不同规模的Hadoop集群上并行运行PCEIGA的加速比进行了比较。加速比的计算公式如下：

(6)

加速比越大，算法运行时间越少，则算法性能越好。不同规模Hadoop集群上PCEIGA的加速比如图4所示，测试所用Hadoop集群除主节点外并行节点数从1到5。

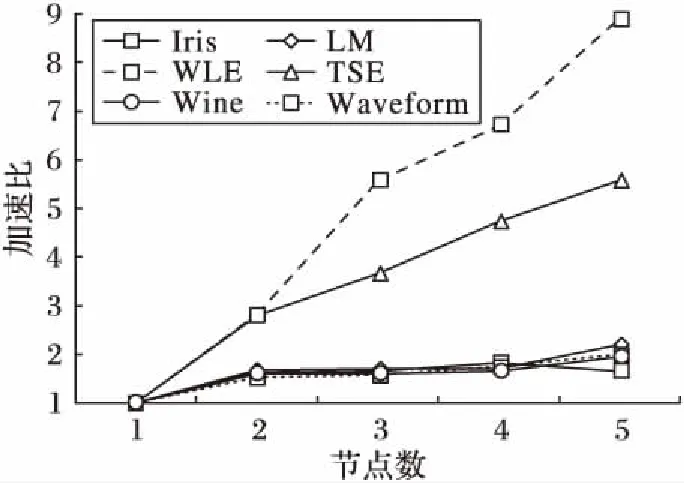
图4　不同规模Hadoop集群上PCEIGA的加速比对比Fig. 4　Speedup comparison of PCEIGA on Hadoop platform with different cluster size

从图4可以看出，在WLE和TSE数据集上，PCEIGA的运行加速比随着机器节点数的增加而快速上升，表明算法运行时间逐渐减少。主要是因为，PCEIGA的两个MapReduce过程中设计的〈key,value〉键值对合理，使算法能够高效运行；PCEIGA在对改进遗传算法进行MapReduce并行时使用combine函数合并map函数的输出，减少了写入磁盘以及通过网络传输到reduce函数的数据量，从而能提高算法运行速度，提高算法加速比。在Iris、LM、Waveform和Wine数据集上，随着节点数的增加，PCEIGA的加速比上升比较缓慢。主要是由于对于数据量较小的数据集采用并行框架会增加时间开支和节点间的通信开销，从而降低算法效率。相比小型数据集，采用Hadoop并行框架运行PCEIGA更适合于大型数据集。但受Hadoop的MapReduce本身开销的影响，加速比的提升是有上限的。为了进一步分析PCEIGA的性能，计算不同规模Hadoop集群并行运行PCEIGA的聚类结果与数据集真实划分的ARI，结果如图5所示。

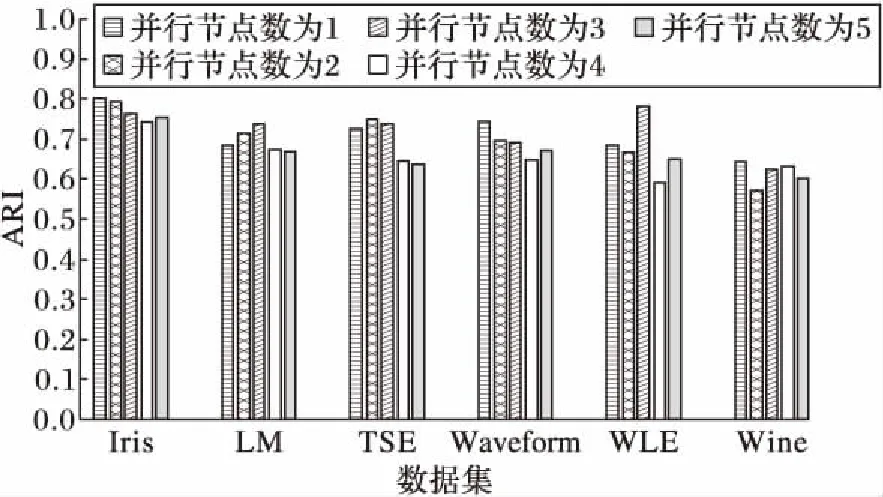
图5　云计算下Hadoop框架运行PCEIGA准确度分析Fig. 5　Accuracy analysis about PCEIGA algorithm on Hadoop platform in cloud computing

由图5可知，PCEIGA在LM、TSE和WLE数据集上多个节点的算法ARI值并不低于单个节点的ARI值，甚至在LM和TSE数据集上，节点数据为2和3时算法的聚类质量明显高于单个节点的PCEIGA的结果质量；在WLE数据集上，节点数据为3时算法的聚类质量明显高于单个节点的PCEIGA的结果质量。在Iris、Waveform和Wine数据集上，单个节点上PCEIGA的ARI值以0.04的优势胜于多个节点的PCEIGA。出现这种现象的原因是，与单个节点的算法运行相比，多个节点并行时，节点之间的通信产生的误差也会导致最终聚类结果质量的下降，但这个误差在可控范围内。因此，可以看出，随着节点数的增加，PCEIGA的聚类准确度会轻微上下浮动，但是在提高运行速度的前提下，这一现象是可以接受的。

综上所述，随着Hadoop框架下节点数的增加，PCEIGA聚类性能并不会明显降低，同时算法运行的加速比明显提升。

5　结语

本文结合聚类融合的特点提出了CEIGA，设计了基于重叠元素数量的选择算子。对遗传算法选择算子的改进优化使得遗传算法作为聚类融合的一致性集成函数不仅保证了基聚类的多样性，还使得最终聚类结果达到全局最优。

根据聚类融合和改进遗传算法的可并行性提出了PCEIGA，设计了云计算下PCEIGA的Map-Reduce并行模型,通过对基聚类生成机制和改进遗传算法的并行处理，以及Combine过程的加入，能有效提高算法运行效率。

最后在自行搭建的Hadoop分布式平台上完成了CEIGA和PCEIGA的性能分析。实验结果表明，CEIGA在准确度和稳定性上都明显优于CEV、CECSPA、CEAL和CEDS算法，而PCEIGA也能在不影响算法质量的情况下缩短算法运行时间，有利于进行海量数据挖掘。

使用MapReduce模型实现PCEIGA的结果表明，随着节点数的增加，PCEIGA运行加速比的提升会减弱甚至下降，因此，Hadoop中并行节点的数量选择会是一个重要的研究方向。而遗传算法作为一致性集成函数，除了受选择算子影响外，适应度函数的设计也很重要。适应度函数很复杂时，会对算法复杂度产生影响；反之，适应度函数很简单时，会影响最终结果准确度。因此，后续工作将研究设计一个恰当的适应度函数，以进一步提高算法运行速度和准确度。

参考文献(References)

[1]STREHL A, GHOSH J. Cluster ensembles: a knowledge reuse framework for combining multiple partitions [J]. Journal of Machine Learning Research, 2003, 3(3): 583-617.

[2]TURING A M. Computing machinery and intelligence [J]. Mind, 1950, 59(236): 433-460.

[3]WANG D X, LI L, YU Z W, et al. AP2CE: double affinity propagation based cluster ensemble [C]// Proceedings of the 2013 International Conference on Machine Learning and Cybernetics. Piscataway, NJ: IEEE, 2013:16-23.

[4]YU Z W, HAN G Q, LI L, et al. Adaptive noise immune cluster ensemble using affinity propagation [C]// ICDE 2016: Proceedings of the 2016 IEEE 32nd International Conference on Data Engineering. Piscataway, NJ: IEEE, 2016: 1454-1455.

[5]KAO L J, HUANG Y P. Ejecting outliers to enhance robustness of fuzzy cluster ensemble [C]// Proceedings of the 2013 IEEE International Conference on Systems, Man, and Cybernetics. Piscataway, NJ: IEEE, 2013: 3790-3795.

[6]IAM-ON N, BOONGOEN T, GARRETT S, et al. A link-based approach to the cluster ensemble problem [J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2011, 33(12): 2396-2409.

[7]ZHONG C M, YUE X D, ZHANG Z H, et al. A clustering ensemble: two-level-refined co-association matrix with path-based transformation [J]. Pattern Recognition, 2015, 48(8): 2699-2709.

[8]WANG L, ZHANG G Y. Cluster ensemble based image segmentation algorithm [C]// ICICSE 2015: Proceedings of the 2015 Eighth International Conference on Internet Computing for Science and Engineering. Piscataway, NJ: IEEE, 2015: 68-73.

[9]YU Z W, LUO P N, YOU J, et al. Incremental semi-supervised clustering ensemble for high dimensional data clustering [J]. IEEE Transactions on Knowledge & Data Engineering, 2016, 28(3): 701-714.

[10]ZHANG S H, YANG L, XIE D Q. Unsupervised evaluation of cluster ensemble solutions [C]// ICACI 2015: Proceedings of the 2015 Seventh International Conference on Advanced Computational Intelligence. Piscataway, NJ: IEEE, 2015: 101-106.

[11]BANERJEE B, BOVOLO F, BHATTACHARYA A, et al. A new self-training-based unsupervised satellite image classification technique using cluster ensemble strategy [J]. IEEE Geoscience & Remote Sensing Letters, 2015, 12(4): 741-745.

[12]YU Z W, CHEN H T, YOU J, et al. Hybrid fuzzy cluster ensemble framework for tumor clustering from biomolecular data [J]. IEEE/ACM Transactions on Computational Biology & Bioinformatics, 2013, 10(3): 657-670.

[13]GOSWAMI J P, MAHANTA A K. A genetic algorithm based ensemble approach for categorical data clustering [C]// INDICON 2015: Proceedings of the 2015 Annual IEEE India Conference. Piscataway, NJ: IEEE, 2015: 1-6.

[14]ALFRED R, CHIYE G J, OBIT J H, et al. A genetic algorithm based clustering ensemble approach to learning relational databases [J]. Advanced Science Letters, 2015, 21(10): 3313-3317.

[15]刘朋欢.基于生成模型的聚类融合算法[D].青岛：中国海洋大学,2014. (LIU P H. Generative approaches for ensemble clustering [D]. Qingdao: Ocean University of China, 2014.)

[16]DEAN J, GHEMAWAT S. MapReduce: simplified data processing on large clusters [C]// Proceedings of the 6th Conference on Symposium on Operating Systems Design & Implementation. Berkeley, CA: USENIX Association, 2008: 10-10.

[17]吴晓璇,倪志伟,倪丽萍.云计算环境下基于分形的聚类融合算法研究[J].计算机工程与应用,2015,51(14):1-6. (WU X X, NI Z W, NI L P. Research on fractal clustering ensemble algorithm based on cloud computing environment [J]. Computer Engineering and Applications, 2015, 51(14): 1-6.)

[18]BENMOUNAH Z, BATOUCHE M. A parallel distributed system for gene expression profiling based on clustering ensemble and distributed optimization [C]// ICA3PP 2013: Proceedings of the 13th International Conference on Algorithms and Architectures for Parallel Processing, LNCS 8285. Cham: Springer, 2013: 176-185.

[19]IAM-ON N, BOONGOEN T. Comparative study of matrix refinement approaches for ensemble clustering [J]. Machine Learning, 2015, 98(1/2): 269-300.

[20]LI F J, QIAN Y H, WANG J T, et al. Multigranulation information fusion: a Dempster-Shafer evidence theory based clustering ensemble method [C]// Proceedings of the 2015 IEEE International Conference on Machine Learning and Cybernetics. Piscataway, NJ: IEEE, 2015: 58-63.