基于反向学习的自适应差分进化算法
李龙澍,翁晴晴
(安徽大学 计算机科学与技术学院,合肥 230601)(*通信作者电子邮箱ahuwqq@126.com)
0 引言
1997年,Storn等[1]提出了一种简单且高效的差分进化(Differential Evolution, DE)算法。该算法具有良好的收敛性及简单易懂的特性,在解决全局优化问题中受到越来越多研究者的青睐,被广泛应用于解决工程设计优化[2]、人工神经网络[3]等问题。
但是,标准差分进化算法需要设计者根据先验知识提前设置缩放因子F和交叉概率Cr,在算法进化过程中无法根据进化方向和优化问题的复杂性动态地改变控制参数的取值,致使在处理高维问题及多峰值问题时算法易陷入局部最优而过早收敛[4-5];另外在算法后期时,种群往往集中于最优值附近,导致种群的多样性减少,无法产生更好的个体。因此,许多研究者集中于差分进化算法自适应方面的研究[6-8]。其中,SaDE(Self-adaptive Differential Evolution)算法[9]首次实现动态调整缩放因子F及交叉概率Cr,其通过高斯分布动态地调整F和Cr的取值。另外一种是由Brest等[10]提出的自适应参数差分进化jDE(self-adapting control parameters in Differential Evolution)算法,利用均匀分布调整相关的控制参数,并采用启发式规则为每一个体赋予不同的值。最经典的自适应差分进化算法是由Zhang等[11]提出的自适应差分进化JADE(Adaptive Differential Evolution with optional external archive)算法,其采用了一种全新的current-to-pbest/1变异策略,即在每一次迭代过程中,从100*p(p为概率)种群中随机选取一个个体作为当前最优个体,并应用于变异策略中;另外利用柯西分布和标准正态分布动态地更新F和Cr,提高了种群向最优值聚拢的速度。Tanabe等[12]在JADE的基础上提出了SHADE(Success-History based parameter Adaptation for Differential Evolution)算法,其利用每一代控制参数的平均值来引导控制参数动态调整,提高了算法的鲁棒性,使得该算法运行更加稳定。Yi等[13]在JADE的基础上提出了pbest-JADE算法,该算法在100*p种群中使用轮盘赌的方式选择最优个体,进一步提高了算法的收敛性和精确性。
以上研究主要集中于自适应差分进化算法的控制参数调整和变异策略的改进,并没有考虑到每代种群中单个个体的局部开发能力。研究表明在进化算法迭代过程中引入机器学习能够获得更高的收敛精度和收敛速度[14]。这是因为机器学习通过对进化算法迭代搜索过程中所存储的搜索空间、问题特征和种群信息等大量数据进行分析,即在全局优化过程中,通过特征提取等方式提取有用信息引导种群的搜索方向。许多应用领域通过引入机器学习的进化算法都使得收敛速度与问题收敛精度有所提高。
由Tizhoosh[15]提出的反向学习的机器学习方法通过同时对当前解集与其反向解集进行适应度评估,选择更优的解集,用以进行下一迭代过程,以期提高算法整体搜索能力,现已被广泛应用于各智能搜索算法,如差分进化(DE)算法[16]、粒子群优化(Particle Swarm Optimization, PSO)算法[17]、智能蜂群(Artificial Bee Colony, ABC)算法[18]等,以提高算法的收敛速度。 Rahnamayan等[19]首次提出了基于反向学习的差分进化算法,在该算法中,采用基于反向学习的机制来初始化种群。之后越来越多的研究学者提出改进后的基于反向学习的差分进化算法。Omran等[20]结合反向学习、差分进化算法并引入混沌搜索策略提出了CODEQ(Chaotic search, Opposition-based learning for Differential Evolution and Quantum mechanics)算法,较好地解决了种群易陷入局部最优的问题。 Wang 等[21]改进了基础的反向学习的机制,提出了一种基于GOBL(Generalized Opposition-Based Learning)的差分进化算法。实验结果表明,以上改进后的反向学习机制应用于差分进化算法中不仅提高了算法的寻优能力,而且能够保证在较短的时间内收敛到最优值附近。
因此,本文在已有JADE算法的基础上,提出一种增强型反向学习的自适应差分进化(Opposition-based Learning of Adaptive Differential Evolution, OL-ADE)算法,通过反向精英学习,增加种群的局部搜索能力,获取更加精确的最优个体;同时,采用高斯分布随机性提高单个个体的开发能力;提高了种群的多样性,避免算法进入早熟,从而实现整体上平衡全局与局部的搜索能力。为了验证本文OL-ADE算法的性能,采用CEC(Congress on Evolutionary Computation)2014中的6个基准测试函数进行仿真实验,实验结果表明OL-ADE算法具有较高的精确性、收敛性和可靠性。
1 基础概念
1.1 差分进化算法
按照进化过程中控制参数能否根据当前种群进化信息进行动态调整,可将差分进化算法分为普通差分进化算法和适应性差分进化算法。差分进化算法属于贪婪性进化算法,其主要有三个操作,即变异、交叉和选择;算法利用种群中多个个体的差异性作为个体的扰动量,使得算法在跳跃距离和搜索方向上具有自适应性。在标准及其改进的差分进化算法中,变异操作对种群的进化方向起着决定性作用。因而现有的改进方法都是在原有变异策略基础上加入新的选择或评判标准,以期提高算法整体性能。以下列举了应用较广泛的适应性差分进化算法的几种变异策略[13]:
DE/best/1:
vi(t)=xbest(t)+Fi(xr1(t)-xr2(t))
(1)
DE/current-to-best/1:
vi(t)=xi(t)+Fi(xbest(t)-xr1(t))+
Fi(xr1(t)-xr2(t))
(2)
DE/current-to-pbest/1:
vi(t)=xi(t)+Fi(xpbest(t)-xr1(t))+
Fi(xr1(t)-xr2(t))
(3)
其中:Fi为适应性差分进化算法中随迭代次数增加而动态调整的缩放因子,取值范围为(0,1);xr1(t)、xr2(t)和xr3(t)是从当前代数种群集合{1,2,…,NP}{i}中随机选择的互不相同的个体;xpbest(t)为当前种群中最优个体;NP表示种群规模大小。
1.2 反向学习
Tizhoosh[15]提出的反向学习是用于机器学习的一种优化策略,即在算法每一次迭代时,同时检测这些当前解的所有反向解,并从当前解集合与反向解集合中选择更利于算法进化的解,从而减少算法的盲目性。随着反向学习的发展,越来越多的研究学者开始关注这一机器学习算法,并在改进反向学习方法的工作中取得了较好的成果。以下对基本反向学习及几种改进的反向学习作简单介绍。相关概念定义如下:
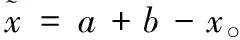
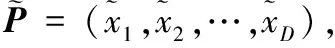
(4)
在Rahnamayan等[22]于2007年提出的QODE(Quasi Oppositional Differential Evolution)算法中,对反向学习作出如下改进:
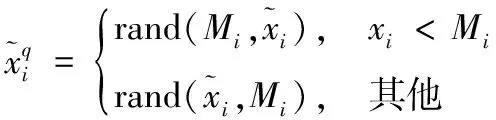
(5)
Mi=(ai+bi)/2
(6)
其中rand(x,y)为在区间(x,y)均匀分布的随机数。数理逻辑证明,在黑盒优化问题中,通过改进后的QODE所求得的拟反向解更接近优化问题的最优解。
Wang等[23]于2011年提出了GOBL策略,在反向求解的过程中通过引入权重来控制反向解的取值范围:
(7)
其中k为(0,1)区间的随机数。
在Seif等[24]于2015年所发表的文章中引入了新的反向解集求解模式,如式(8)所示:
(8)
与式(8)所求反向解对应的是根据原有解集通过均匀分布获得与当前反向解相对的反向解集,如式(9)所示,通过对三个解集的评估,选取其中最优解。
(9)
2 OL-ADE算法
由于优化问题复杂性各不相同,而同一问题在不同的进化阶段所需的变异策略和控制参数也应有所改变。因此,如何在差分进化算法进化过程中动态调控控制参数取值一直是研究的创新点与热点。由于JADE算法的变异策略是从100*p(p为概率)个种群中随机选取一个个体作为xpbest取代当前最优个体用以变异操作,该策略丰富了种群多样性也降低了差分进化算法的收敛速度。而本文在JADE算法的基础上提出一种基于反向学习的变异策略,对用于变异操作的个体定义了新的选择标准,具体如下:
vi(t)=φi(t)+Fi(xopbest(t)-φi(t))+
Fi(xr1(t)-xr2(t))
(10)
其中:xopbest和φi由本文所述方式进行选择;xr1、xr2为随机选择的互不相同的个体;Fi使用JADE中的方式确定。
2.1 基于反向学习的最优个体xopbest的选择
在JADE中, 100*p个个体为精英种群,从中随机选择一个个体作为最优个体。本文采用如下过程获取最优个体:
1)随机取精英种群NP1={x1(t),x2(t),…,xN(t)},xi(t)=(xi,1(t),xi,2(t),…,xi, j(t),…,xi,D(t)),其中N=100*p,i=1,2,…,N。
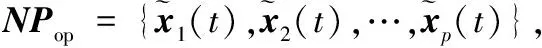
M=(x1+x2+…+xN)/N
(11)
(12)
其中:i=1,2,…,N,j=1,2,…D,N为精英种群中个体个数。充分利用精英种群中每一个体信息求取反向精英种群,这一策略提高了算法的探测能力,进而增强算法的整体寻优能力。
3)从NP1∪NPop中选择适应度值最好的个体xxbest,并计算xmean=(x1+x2+…+x2N)/2N,利用式(13)计算xopbest:
(13)
根据此方法求得xopbest能够保证算法在更大的搜索空间内搜寻最优值,从而引导个体向最优值进化,提高算法的收敛速度。
2.2 φi 的选择标准
许多改进的智能优化算法都继承了原算法过早收敛的特性,差分进化算法亦是如此。而本文根据反向学习机制确定的xopbest的选择标准,虽然提高了算法的局部搜索能力,增加了最优解的精确度,但在多峰值问题寻优过程中,同其他差分进化算法一样,容易陷入局部最优。为解决这一问题,本文在一定的概率下对用于变异阶段的个体引入高斯分布随机搜索,在每个个体搜索可行解的过程中进行扰动,提高单个个体的开发能力,具体如下:
(14)
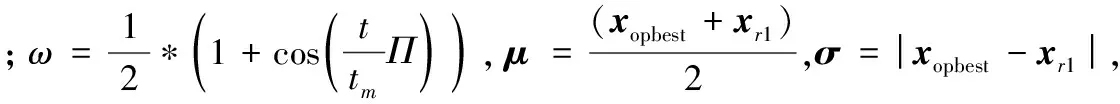
2.3 改进的自适应差分进化算法
不同于现有的一些反向学习应用于算法的种群初始化阶段,本文将其应用于差分进化算法的选择策略中,这样减少了算法对大量冗余数据的计算量;且本文算法选择自适应的差分进化算法,即将反向学习机制与自适应机制中最优个体的选择相结合,选择出更适用于变异策略的最优个体。原有的自适应差分进化算法用于变异策略的个体种群为NP1,而经过反向学习机制后,形成的反向解集NPop可以加强算法对精英个体邻域的探测,即将原有NP1与现有NPop相结合,反向精英个体也参与竞争,选择当前适应度值最好的个体,并利用式(13)计算出xopbest。
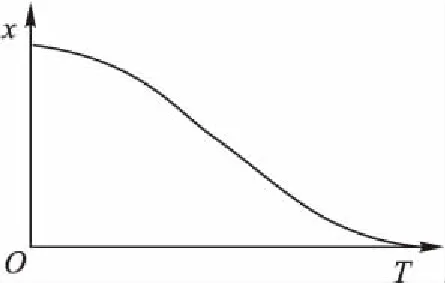
图1 个体间差异曲线Fig. 1 Individual difference curve
在差分进化算法中,基于反向学习的xopbest的选择不仅保证算法能在更大的搜索空间内搜寻最优值,而且还提高了算法的局部搜索能力,提高了算法的收敛速度。同时利用高斯分布进行φi个体的选择,丰富了种群多样性,减轻了算法因应用反向学习所带来的过早收敛的压力。φi与xopbest相结合,在增强种群局部搜索能力的同时,整体上平衡了全局搜索与局部寻优的能力。自适应控制参数的引入,能够动态调整算法中的各个控制参数,减少人为设置参数的影响。OL-ADE伪代码具体如算法1。
算法1Procedure of OL-ADE。
1)
Begin
2)
SetμCR=0.5;μF=0.5;p=0.05;c=0.1;
//μCR为交叉概率,μF为缩放因子,
//p为选择精英种群的概率,c为常量
3)
Initial population {xi(0)|i=1,2,…,NP}
4)
Fort=1 toT
5)
SCR=∅;SF=∅;
//SCR和SF分别存放变异及
//交叉成功的后代个体所对应的自适应的μF和μCR
6)
Fori=1 toNP
7)
GenerateCRi=rand(μCR,0.1),Fi=rand(μF,0.1);
8)
Choosexopbestby formulate (13);
9)
Randomly choosexr1(t)≠xi(t) from current populationP;
10)
Randomly choosexr2(t)≠xi(t) andxr1(t)≠xr2(t) from current populationP;
11)
vi(t)=φi(t)+Fi(xopbest(t)-φi(t))+
Fi(xr1(t)-xr2(t))
12)
Generatejrand=rand(1,D)
13)
Forj=1 toD
14)
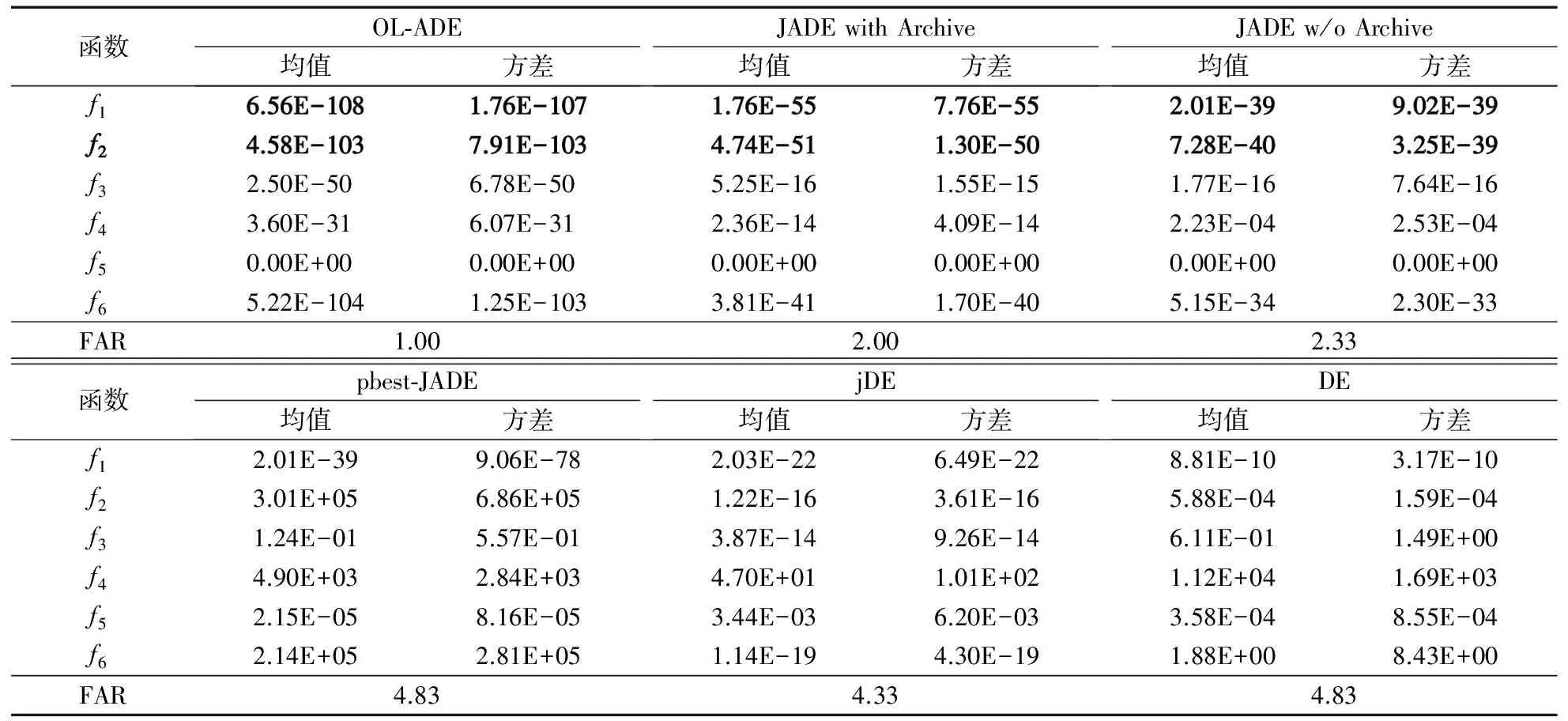
Ifj=jrandor rand(0,1) 15) ui, j(t)=vi, j(t); 16) Elseui, j(t)=xi, j(t); 17) End for 18) Iff(xi(t))≤f(ui(t)) 19) xi(t+1)=ui(t);CRi→SCR;Fi→SF; 20) Elsexi(t+1)=xi(t) 21) End for 22) μCR=(1-c)·μCR+c·meanA(SCR); //meanA(SCR)表示算术平均值 23) μF=(1-c)·μF+c·meanL(SF); //meanL(SF)表示Lehmer平均值 24) t=t+1 25) End for 26) End 在对比实验中,本文研究选择了四个经典的差分进化算法包括DE、jDE、JADE和pbest-JADE进行对比,其中JADE又分为存档JADE(JADE with Archive)和不存档JADE(JADE w/o Archive)。 为评估本文所提方法的性能,从CEC 2014上选择如下6个基准函数进行实验: 为了保证实验的公平性,实验参数值设为文献[13]建议的参数值,即μCR=0.5,μF=0.5;p=0.05;c=0.1;所有算法种群规模NP=100,维度D=30;另外,每个算法最大迭代次数为2 000;同时,为了减少实验环境对实验结果造成的误差,每个算法独立运行30次。所有实验程序在Matlab R2010a版本下运行,PC环境为Windows操作系统Intel Core i3 CPU 2.0 GHz和4 GB内存。 本组实验主要测试本文算法OL-ADE与其他五种算法在维度为30的情况下独立运行30次所获得的最优解的平均值与方差。 表1中将每一个测试函数中结果最好的以粗体标记,以方便辨识。从表1中可以看到,本文算法的每一测试函数适应值均值与方差都比其他算法低,表明本文算法更加精确地趋于理论最优值,且稳定性较高。为进一步分析实验结果,表1还给出了每个算法的Friedman平均排名(Friedman Average Rank, FAR)[25],可以发现本文算法表现最好。 图2分别展示了在30维情况下这六种对比算法运行6个基准测试函数找到最优解的变化曲线,其中X轴表示算法的迭代次数,Y轴采用log坐标表示函数的适应值。从图2可以看出,本文算法大部分函数的收敛速度要高于其他算法,而且收敛精度也略高于其他算法,主要原因取决于通过反向精英学习能够获得最优当前个体,快速引导算法向最优值靠近。 图2 测试函数收敛曲线(D=30)Fig.2 Convergence curve of test functions (D=30) 为了验证本文算法的可靠性,为每个测试函数的适应值设置一个阈值,观察算法达到阈值的成功率,其中,假定所有函数的阈值为1.0E-5。在表2中列出了每个测试函数到达阈值的平均迭代次数及成功率,其中NA表示在算法达到最大迭代次数时都没有收敛到事先所设置的阈值。另外,为便于辨识,在表2中将每一个测试函数中最好的结果设置为粗体。可以看到,除了f5函数以外,本文OL-ADE都是最先达到预设收敛阈值,体现了OL-ADE算法具有较高的收敛速度。本文方法是通过丰富种群多样性来提高收敛精度,而f5函数的可行解定义域较大,所以OL-ADE算法在进化初期因在可行解定义域内形成的种群丰富度大导致进化初期算法收敛速度较慢,因此达到固定收敛阈值所需迭代次数较多。另外,本文提出的OL-ADE算法的成功率基本上都达到100%,从而表明OL-ADE算法更加可靠。 综上所述,本文算法OL-ADE与DE、jDE、JADE with Archive、JADE w/o Archive 和pbest-JADE相比,在精确性、收敛速度和可靠性上表现更加优越。 表1 测试函数的均值和方差(D=30)Tab. 1 Mean value and standard deviation for test functions (D=30) 表2 不同算法对各测试函数的平均迭代次数和成功率Tab. 2 Average number of iterations and success rate for test functions under different algorithms 本文提出了一种基于反向学习自适应差分进化算法OL-ADE。该算法利用反向学习机制求取反向解集,提高了种群的局部搜索能力;同时在变异阶段引入高斯分布,有效减轻了算法因使用反向学习引起的收敛过快而使得种群陷入局部最优的负担;另外,OL-ADE算法将反向学习与高斯分布相结合,在增强种群局部搜索能力的同时,整体上平衡了全局搜索与局部寻优的能力。最后,本文使用CEC 2014中6个基准测试函数对本文所提算法与其他差分进化算法进行仿真实验,结果表明本文OL-ADE算法收敛更快、精度更高,即OL-ADE算法总体性能和可靠性较高。在下一步工作中,将在多目标优化问题中对增强型反向学习的自适应算法在收敛性及可靠性方面作进一步研究。 参考文献: [1]STORN R, PRICE K. Differential evolution — a simple and efficient heuristic for global optimization over continuous spaces [J]. Journal of Global Optimization, 1997, 11(4): 341-359. [2]LIAO T W. Two hybrid differential evolution algorithms for engineering design optimization [J]. Applied Soft Computing, 2010, 10(4): 1188-1199. [3]PIOTROWSKI A P. Differential evolution algorithms applied to neural network training suffer from stagnation [J]. Applied Soft Computing, 2014, 21: 382-406. [4]ZHOU Y-Z, YI W-C, GAO L, et al. Adaptive differential evolution with sorting crossover rate for continuous optimization problems [J]. IEEE Transactions on Cybernetics, 2017, 47(9): 2742-2753. [5]FAN Q, YAN X. Self-adaptive differential evolution algorithm with zoning evolution of control parameters and adaptive mutation strategies [J]. IEEE Transactions on Cybernetics, 2016, 46(1): 219-232. [6]薛羽,庄毅,顾晶晶,等.自适应离散差分进化算法策略的选择[J]. 软件学报,2014,25(5):984-996. (XUE Y, ZHUANG Y, GU J J, et al. Strategy selecting problem of self-adaptive discrete differential evolution algorithm [J]. Journal of Software, 2014, 25(5): 984-996) [7]YANG M, LI C, CAI Z, et al. Differential evolution with auto-enhanced population diversity [J]. IEEE Transactions on Cybernetics, 2015, 45(2): 302-315. [8]GUO J, LI Z, XIE W, et al. Dissipative differential evolution with self-adaptive control parameters [C]// CEC 2015: Proceedings of the 2015 IEEE Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2015: 3088-3095. [9]QIN A K, SUGANTHAN P N. Self-adaptive differential evolution algorithm for numerical optimization [C]// CEC 2005: Proceedings of the 2005 IEEE Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2005: 1785-1791. [10]BREST J, GREINER S, BOSKOVIC B, et al. Self-adapting control parameters in differential evolution: a comparative study on numerical benchmark problems [J]. IEEE Transactions on Evolutionary Computation, 2006, 10(6): 646-657. [11]ZHANG J, SANDERSON A C. JADE: adaptive differential evolution with optional external archive [J]. IEEE Transactions on Evolutionary Computation, 2009, 13(5): 945-958. [12]TANABE R, FUKUNAGA A. Success-history based parameter adaptation for differential evolution [C]// CEC 2013: Proceedings of the 2013 IEEE Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2013: 71-78. [13]YI W, ZHOU Y, GAO L, et al. An improved adaptive differential evolution algorithm for continuous optimization [J]. Expert Systems with Applications, 2016, 44: 1-12. [14]ZHANG J, ZHAN Z-H, LIN Y, et al. Evolutionary computation meets machine learning: a survey [J]. IEEE Computational Intelligence Magazine, 2011, 6(4): 68-75. [15]TIZHOOSH H R. Opposition-based learning: a new scheme for machine intelligence [C]// CIMCA ’05: Proceedings of the 2005 International Conference on Computational Intelligence for Modelling, Control and Automation and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’06). Washington, DC: IEEE Computer Society, 2005: 695-701. [16]WANG W, WANG H, SUN H, et al. Using opposition-based learning to enhance differential evolution: a comparative study [C]// CEC 2016: Proceedings of the 2016 IEEE Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2016: 71-77. [17]WANG H, LI H, LIU Y, et al. Opposition-based particle swarm algorithm with Cauchy mutation [C]// CEC 2007: Proceedings of the 2007 IEEE Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2007: 4750-4756. [18]EL-ABD M. Opposition-based artificial bee colony algorithm [C]// GECCO ’11: Proceedings of the 13th Annual Conference on Genetic and Evolutionary Computation. New York: ACM, 2011: 109-116. [19]RAHNAMAYAN S, TIZHOOSH H R, SALAMA M M A. Opposition-based differential evolution algorithms [C]// CEC 2006: Proceedings of the 2006 IEEE Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2006: 2010-2017. [20]OMRAN M G H, SALMAN A. Constrained optimization using CODEQ [J]. Chaos, Solitons & Fractals, 2009, 42(2): 662-668. [21]WANG H, RAHNAMAYAN S, WU Z. Parallel differential evolution with self-adapting control parameters and generalized opposition-based learning for solving high-dimensional optimization problems [J]. Journal of Parallel and Distributed Computing, 2013, 73(1): 62-73. [22]RAHNAMAYAN S, TIZHOOSH H R, SALAMA M M A. Quasi-oppositional differential evolution [C]// CEC 2007: Proceedings of the 2007 IEEE Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2007: 2229-2236. [23]WANG H, WU Z, RAHNAMAYAN S, et al. Enhancing particle swarm optimization using generalized opposition-based learning [J]. Information Sciences, 2011, 181(20): 4699-4714. [24]SEIF Z, AHMADI M B. An opposition-based algorithm for function optimization [J]. Engineering Applications of Artificial Intelligence, 2015, 37: 293-306.3 实验分析
3.1 实验参数
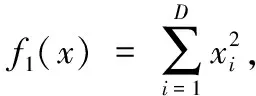

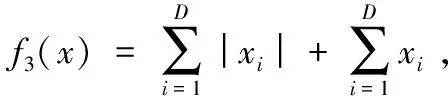
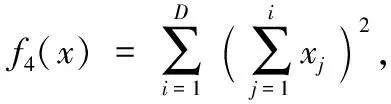
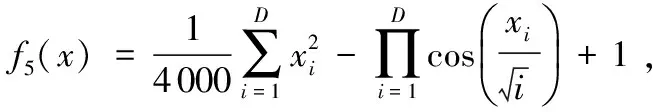
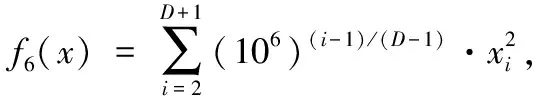
3.2 收敛精度
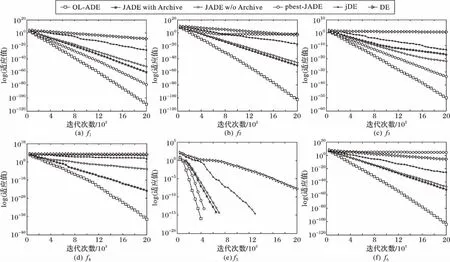
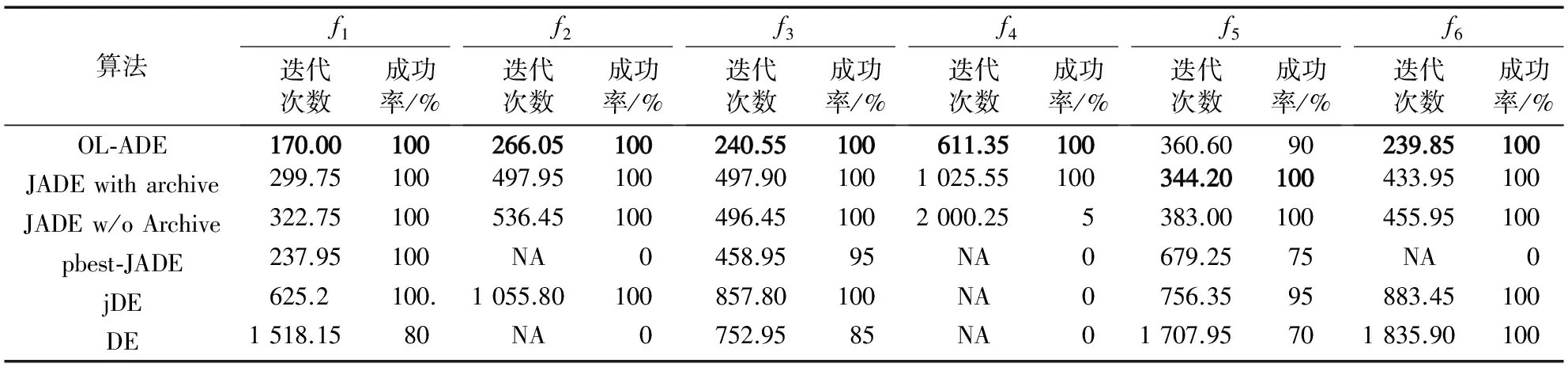
3.3 算法可靠性
4 结语

