例析几柯概型概率的求解方法
概率是高中数学的重要内容,也是每年高考考查的主要内容,特别是与长度或面积有关的几何概型是高考考查的重点。
几何概型的定义:如果每个事件发生的概率只与构成该事件区域的长度、角度、面积或体积成比例,则称这样的概率模型为几何概率模型,简称为几何概型。
几何概型的特点:试验中所有可能出现的结果(基本事件)有无限多个;每个基本事件出现的可能性相等。
下面举例说明几何概型的几种题型的求解方法。
一、求角度型几何概型的概率
例1如图1所示,在等腰直角三角形A B C中,过直角顶点C在∠A C B内作一条射线CM,与线段A B交于点M,求AM<A C的概率。
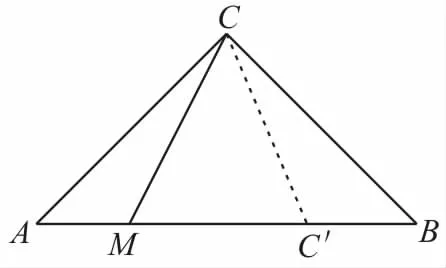
图1
解:在A B上取点C',使得A C'=A C,则
又∠A C B=90°,所以根据几何概型概率计算公式可得所求概率
本题考查与角度有关的几何概型的概率的求法。由于随机事件的区域是角度,所以解题的关键是用角度来刻画射线CM随机地落在∠A C B内,可知∠A C B为所有试验结果构成的区域,当射线CM落在∠A C C'内时,AM<A C,故∠A C C'为构成事件的区域。
二、求面积型几何概型的概率
例2如图2所示,正方形A B C D内的图形来自中国古代的太极图。正方形内切圆中的黑色部分和白色部分关于正方形的中心对称。在正方形内随机取一点,则此点取自黑色部分的概率是 。

图2
解:根据题意可知正方形内切圆中黑色部分的面积与白色部分的面积相等。
设正方形的边长为a,则S正方形ABCD=a2,根据几何概型概率计算公式可得所求概率P=
本题考查与面积有关的几何概型的概率的求法。解答本题的关键是利用圆中黑色部分的面积与白色部分的面积相等求出黑色部分的面积。
三、求体积型几何概型的概率
例3有一杯2L的水,其中含有1个细菌,用一个小杯从这杯水中取出0.1L,求小杯水中含有这个细菌的概率。
解:记“小杯水中含有这个细菌”为事件A,事情A的概率只与取出水的体积有关,这符合几何概型的特征。
因为用小杯取水0.1L,原杯中有水2L,所以根据几何概型概率计算公式可得所求概率
本题考查与体积有关的几何概型的概率的求法。解答本题的关键是判断出该问题为几何概型,利用体积比求概率。

