基于可变带宽的Mean Shift音频聚类算法
向 伟
0 引言
近年来,广播新闻语料、电台语音等现实世界中的语音信号已经成为了研究重点.在现有的音频数据中,同一音频中不同的时间段往往对应不同的说话人或者不同录制环境的语音,因此有必要将其中具有不同特性的音频数据分成不同的段,然后将具有相同特性的音频段聚到一起,为提高音频检索系统的性能打下基础.
由于对于一个未知的音频流,了解其先验知识不太实际,因此本文采用Mean Shift算法进行聚类.[1-3]Mean Shift算法不需要任何先验条件,数据集中的每一点都可作为初始点,分别执行Mean Shift算法,收敛到同一个点算作一类,它能对任何维度、任何分布的采样点进行聚类.针对文献中固定带宽的Mean Shift算法对聚类结果的影响,[4]本文采用基于可变带宽的Mean Shift音频算法.
本文的聚类算法首先提取了基于小波变换的MFCC倒谱系数,然后对小波域音频特征进行PCA变换处理,最后采用可变带宽的Mean Shift算法,并输出聚类结果.
1 基于小波变换的Mel倒谱系数
MFCC是通过模拟人耳听觉特性提取出的一种参数,该特征能很好的模拟人耳听觉系统,在说话人识别,音频分割和聚类,音频检索中广泛采用的一种参数.MFCC参数提取过程如图1所示:
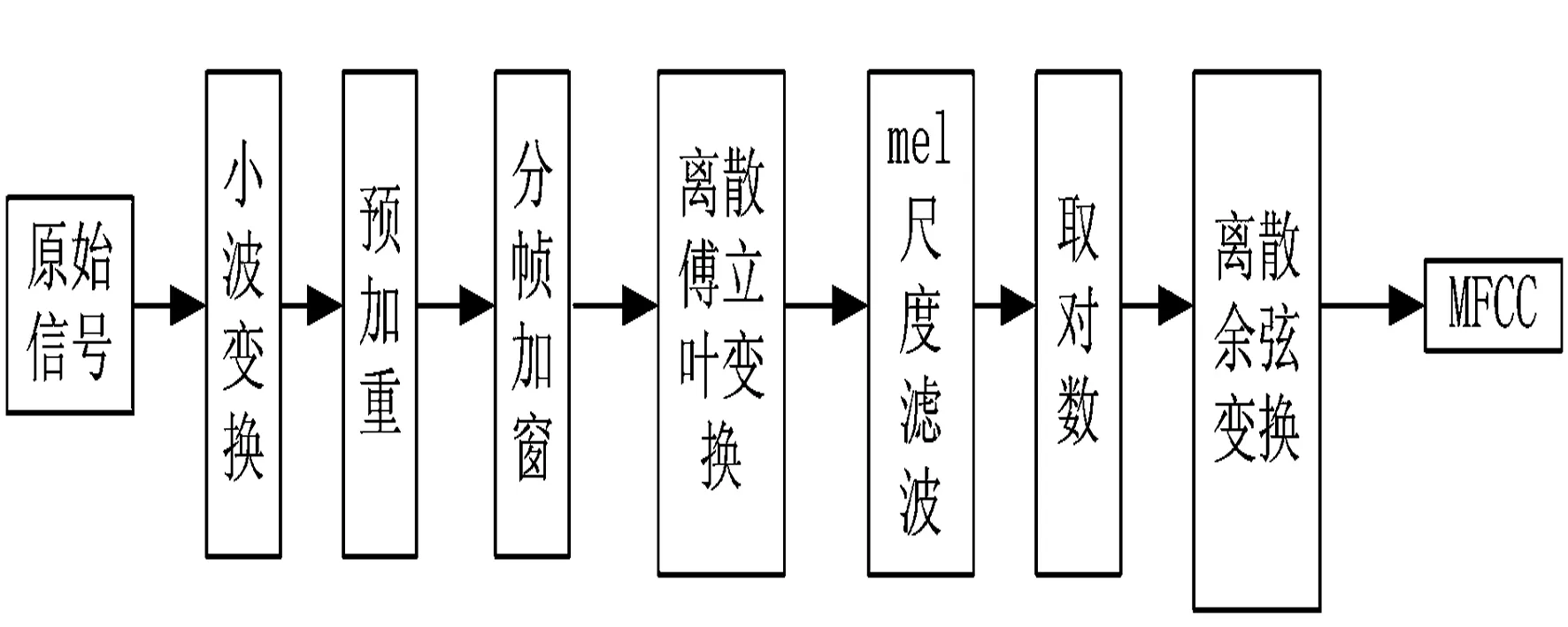
图1 MFCC参数提取流程图
Mel尺度频率域提取的倒谱特征系数,MFCC提取过程如下:
Step1:输入的原始音频信号经过小波变换,最后经小波变换后的低频信号经过预加重、加窗分帧处理,然后做离散傅立叶变换,获得频谱分布.设音频信号的DFT为:
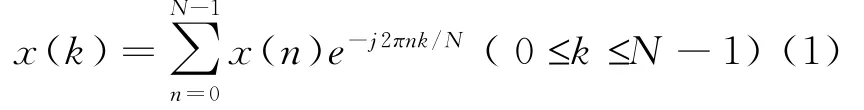
式中x(n)为输入的音频信号的低频信号;N表示傅立叶变换的点数.
Step2:将能量谱通过Mel滤波器组进行带通滤波,并对每个频带的能量进行叠加得到频谱能量xa(k);
Step3:将每个滤波器组输出的频谱能量取对数:然后经离散余弦变换(DCT)得到 MFCC系数:
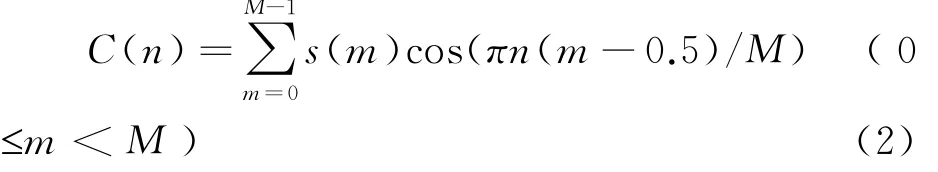
其中M为滤波器个数,s(m)为频谱能量取对数.
2 PCA特征预处理
音频分割出的每个音频段具有相同的声学特征,对每个音频段进取小波域MFCC特征,作为聚类算法的输入.但是这些被分割开的音频段,大多不只一秒,有些甚至是几十秒,如何从这些大小不一的音频段中提取出最重要的特征向量,来表示整个音频段数据.一些文献中使用PCA变换来对提取的特征数据进行降维,[5,6]取得比较好的效果.本文中采用主成分分析来选取能更好表示音频段的特征.
主成分析(PCA)是一种经典的统计方法,通过可逆线性变换,将高维数据特征转换为维数较少的特征,对数据进行分析的技术,对原有样本数据进行简化.简单的说,该方法可以有效的找出数据中最“主要”的元素和结构,从而去除原数据间的相关性和冗余信息,将原有的复杂数据降维.因此被广泛应用于数据挖掘、模式识别,信号探测等领域.
PCA的原理,设x表示m维向量xt,通过公式(3)PCA将m维向量xt线性变换为新的s维向量

其中,U表示一个m×m的正交矩阵,它的第i列ui是样本协方差矩阵的第i个特征向量.PCA需首先求解公式(4)的特征值
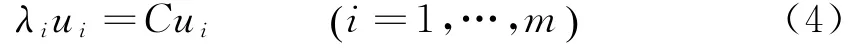
公式(4)中,λi表示C的第i个特征值,ui是相应的特征向量.协方差矩阵C的特征值按降序排列λ1⩾λ2⩾…⩾λm⩾0,相应的特征向量构成矩阵U=u1,u2,…,um[].计算出ui后,向量yt可以通过公式(5)对向量xt进行正交变化得到.
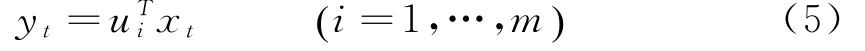
3 可变带宽的Mean Shift算法
本文中采用可变带宽的Mean Shift算法[7]进行音频段的聚类.即对不同的样本数据我们选择不同的带宽h=h(xi),则可变带宽的核函数密度估计变为:
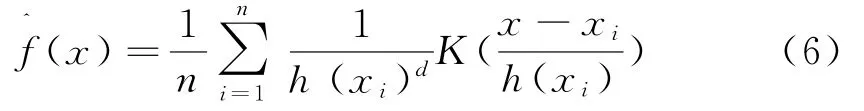
其中
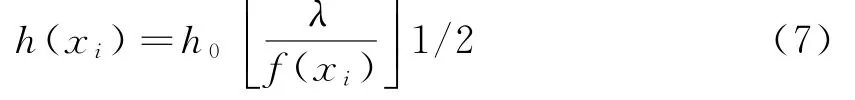
公式(7)中h0是固定带宽,λ为比例常数.
定义1:X代表一个d维的欧氏空间,x是该空间中的一个点,用一列向量表示.x的模‖x‖2=xTx.R表示实数域.如果一个函数K:X→R存在一个剖面函数k:[0,¥]→R,即

并且满足:
(1)k x()为非负;
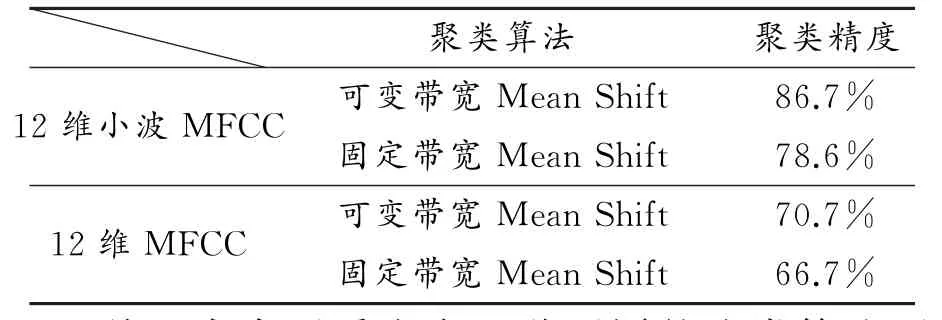
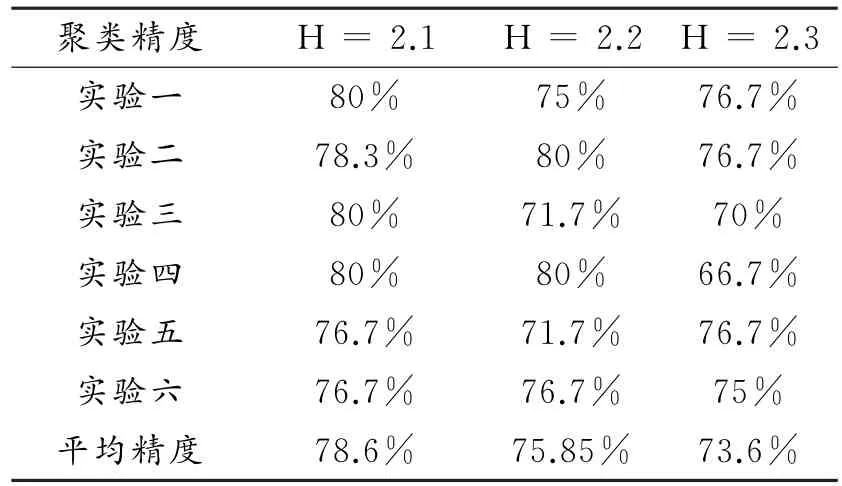
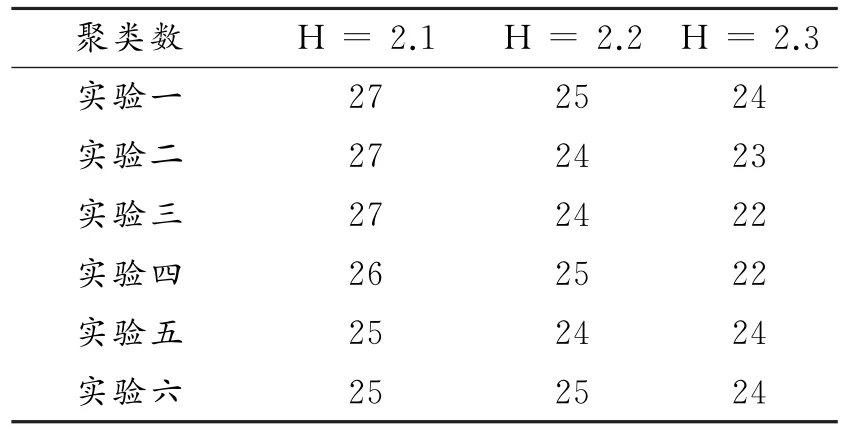
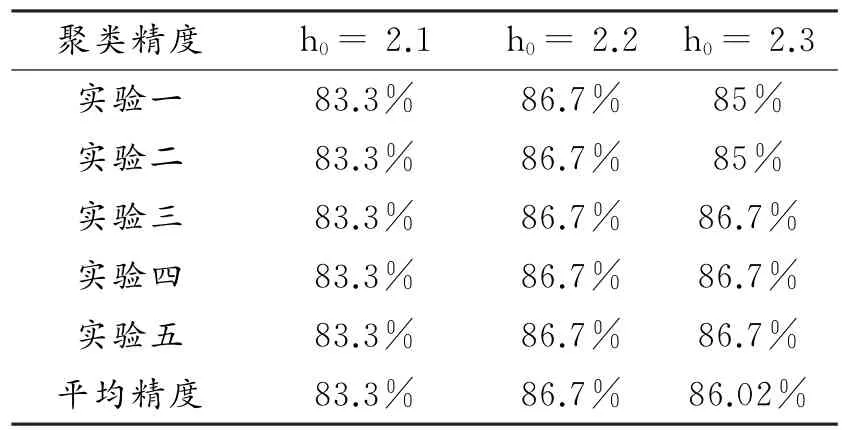
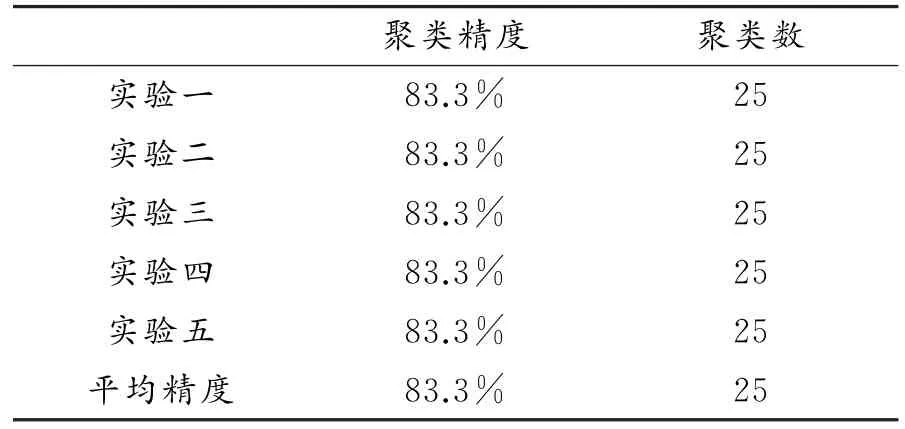
(2)k x()非单调递增,即如果a 那么函数k x()就被称为核函数.本文中的可变带宽Mean Shift算法使用的核函数为高斯核函数,它的估计更准确,收敛路径更平滑.即 用hi表示式(6)中的h(xi),i=1,...,n,则样本点的核函数密度估计可写为 设g(x)=-k'(x),则由式(10)可得可变带宽的密度梯度估计为 设G(x)=Cg(‖x‖2),则可变带宽的Mean Shift向量为: 高考数学北京卷压轴题(第20题)考察角度之一是学生是否具有在全新的问题情境下,自觉地进行探究、尝试、归纳、猜想和论证而创造性地解决问题的能力(参考[6][9]).这些试题一贯的新颖大气,特色鲜明,是北京卷的标志性题目,历年来引起广大师生的重视,依我们拙见,这些题目主要具有以下几方面的特点. 其中C是归一化常数.将式(7)代入,根据式(11)中得: 其中 则可变带宽的Mean Shift向量为:因此Mean Shift向量Mh(x)总是指向概率密度增加最大的方向,说明局部均值朝附近数据样本密集区域移动,可推导出核函数中心从当前位置yj移动到yj+1的表达式为: 由公式(12)有Mean Shift迭代公式: 给定样本数据集 xi{}i=1...n,可变带宽Mean Shift算法中与每个数据样本相适应的带宽,具体步骤如下: Step1:根据给定的固定的初始带宽h0,和样本数据求出样本数据点的密度估计f(xi); Step2:计算公式(7)中的λ;则 计算出每个音频数据段的自适应带宽后,执行可变带宽的Mean Shift音频聚类算法,具体步骤如下: Step 1:特征空间中随机选择初始点xi,根据该数据点的自适应带宽h(xi),计算出其相应的结束条件εi; Step 2:根据公式(16)计算出yj+1; Step 3:判断是否满足条件 yj+1-yj<εi,如果满足,则退出 Mean Shift迭代过程;否则,用yj+1代替yj,转到Step2继续进行迭代. 实验中使用的音频数据来自于VOA的广播新闻和CD音乐,数据的采样频率为11.025 K HZ,精度为16位.该数据集由60段长度不等的音频数据组成,时间长度在15秒至80秒之间,其内容包括男女播音员的标准语音、外景采访人员和被采访人员语音、演讲现场音频、电话录音音乐以及噪音等.这60段音频数据中具体的实际类别如表1所示.为了使聚类结果更细化,我们将属于同一声学条件的音频段分为一类,本文设计将音频段聚成应该有的类,将文献中固定带宽的Mean Shift算法的聚类类别进行细化,不只是将音频段分为男播音、女播音、外景采访和音乐四类,而是将同一说话人或同一声学条件无监督的聚为一类. 表1 实验数据 聚类的正确率采用公式(18)来衡量: 聚类的正确率=聚类正确的音频段/所有的音频总数(18) 将本文设计的聚类算法采用基于小波变换的MFCC参数,由于特征参数的不同选择的初始带宽不同,选择与特征参数最优的带宽进行比较.并采用两种不同的聚类算法对选取的特征进行聚类结果比较,分别是可变带宽的Mean Shift聚类算法和固定带宽的Mean Shift聚类算法.因此可变带宽的Mean Shift算法中12维小波MFCC参数的初始带宽为2.2,所以12维特征参数采用的最优初始带宽为1.9;固定带宽的Mean Shift算法中最优的固定带宽选择分别为2.1和1.9.本文采用的12维小波MFCC特征和12维MFCC参数聚类性能的比较.如表2所示. 表2 不同特征参数的聚类性能比较 从上表中可看出在两种不同的聚类算法下12维小波MFCC特征比没经过小波变换的特征参数都提高了,其中固定带宽的聚类算法提高了12%左右,可变带宽的聚类算法提高了16%左右.因此本文提出的基于可变带宽的Mean Shift聚类算法采用的特征经小波变换的MFCC特征. 实验发现固定带宽的Mean Shift聚类算法中固定带宽的选择对结果影响较大,随着带宽值的增加,聚类的类别在减少,相对来说聚类的精度在提高.按本文聚类算法的设计思想,是将聚类的结果更加的细化.本文中可变带宽的Mean Shift算法聚类结果与固定带宽的结果是在将聚类结果细化的基础上进行的比较. 表3是固定带宽的Mean Shift算法实验结果.表4所示为固定带宽输出的聚类数.其中带宽选取小于2.1时,其聚类结果更细化,属于同类的被分开;而大于2.3时,其聚类的类数更少,把不属于同一类的样本聚成了一类.实验中选取2.1,2.2,2.3三个带宽值进行比较,由于Mean Shift算法是随机选取一个点作为初始点,这种随机性造成了结果的不稳定,所以对每个带宽值进行多次实验. 表3 固定带宽的实验结果 表4 固定带宽输出类数 从表3,4中可以看出固定带宽的Mean Shift受带宽的影响较大,而且这种固定带宽的Mean Shift聚类算法受初始点随机性的影响,其结果不稳定,输出的聚类数也不稳定. 表5 可变带宽的实验结果 如表5所示,我们给出了可变带宽的Mean Shift聚类算法的结果,在同样的样本数据上,初始带宽h0我们也选取2.1,2.2,2.3这三个值作为初始带宽h0,可变带宽的Mean Shift根据样本点和这个初始带宽求出每个样本数据相适应带宽,再进行聚类算法.表5是可变带宽Mean Shift聚类算法的聚类精度. 从表中可看出采用可变带宽的Mean Shift算法的聚类结果相对较稳定,只是样本数据中少量的样本有变动.采用这三个初始带宽h0输出的聚类数分别为24、22和22,输出的聚类数没有变动.对比固定带宽的Mean Shift算法和可变带宽的Mean Shift算法,不只是聚类结果趋于稳定,而且聚类精度也提高了6%~8%. 本文中改进的Mean Shift聚类算法输入的特征是经PCA变换后的音频特征,为了比较本文采用PCA变换之后对聚类精度的影响,将这种变换后的聚类算法与没有经PCA变换后的聚类算法进行实验结果对比.也进行五次实验结果对比,采用的初始带宽值为2.2. 表6 未经PCA变换的聚类实验结果 从表6可看出经PCA变换的聚类算法与未经PCA变换的聚类精度提高了3.4%,这是因为经PCA变换后去除了样本音频数据之间的相关性和音频数据的冗余性,使经PCA变换后的音频特征更能表示该音频数据的语义信息,从而提高了聚类精度.而且从表中还可看出采用可变带宽的算法相对于固定带宽的聚类算法的聚类结果要稳定,采用可变带宽的Mean Shift算法随机选择初始点的这种随机性影响要小得多. 本文设计的音频聚类算法首先对音频段提取基于小波变换的MFCC特征,并将经PCA变换后的小波MFCC特征作为可变带宽的Mean Shift算法的输入,然后输出音频聚类结果.从上述实验结果可看出本文设计的可变带宽的聚类算法比固定带宽的聚类算法明显有提高,而且减小了随机性的影响,使得聚类的结果趋于稳定. 参考文献: [1]Fukunaga K,L Hostetler.The esti mation of the gr adient of a density f unction,with ap plications in patter n recognition[J].IEEE Transactions on Infor mation Theory,1975(1):32-40. [2]Co maniciu D,Meer P.Mean shift:a robust approach towar d feature space anal ysis[J].IEEE Transactions on Patter n Analysis and Machine Intelligence,2002(24):603-619. [3]Cheng Y Z.Mean shift,mode seeking,and cl ustering[J].IEEE Transactions on Patter n Analysis and Machine Intelligence,1995(8):790-799. [4]郑继明,俞 佳.基于Mean-Shift的广播音频聚类算法[J].计算机应用,2009(10):2741-2743. [5]J Hung,H Wang,and L Lee.Automatic metric based speech seg mentation for broadcast news via principal co mponent anal ysis[C]//Proceedings of the 6thInter national Conference on Spoken Language Pr ocessing,2004(4):121-124. [6]刑玉娟,李 明,张亚芬.基于PCA和核Fisher判别的说话人确认[J].计算机工程与设计,2008(15):3984-3986. [7]Co maniciu D,Meer P.The variable band with mean shift and data-driven scale selection[C]//Proceedings Eighth IEEE Inter national Conference,2001(1):438-445. [8]文 武,姜 涛.融合SIFT和尺度方向自适应的Mean shift目标跟踪算法[J].微电子学与计算机,2015(10):93-97. [9]丁业兵.基于惯量矩的自适应带宽Mean shift目标跟踪算法[J].计算机应用与软件,2016(7):321:325.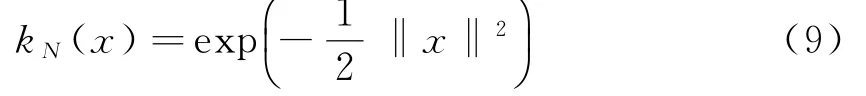
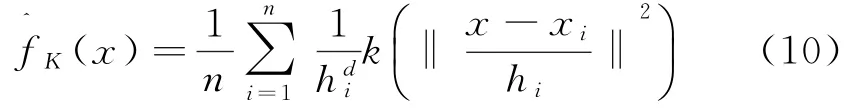

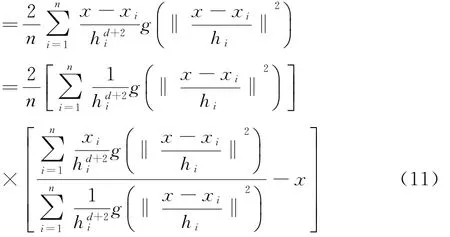
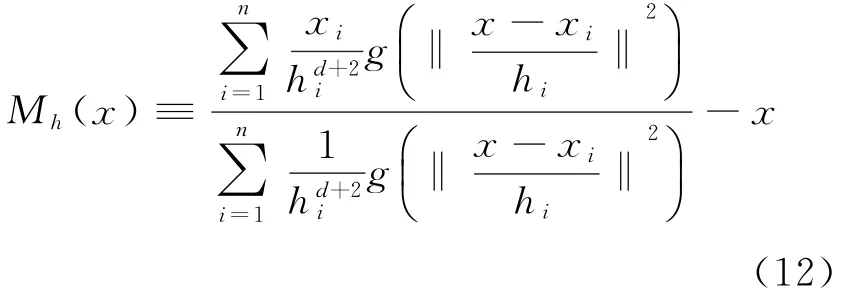
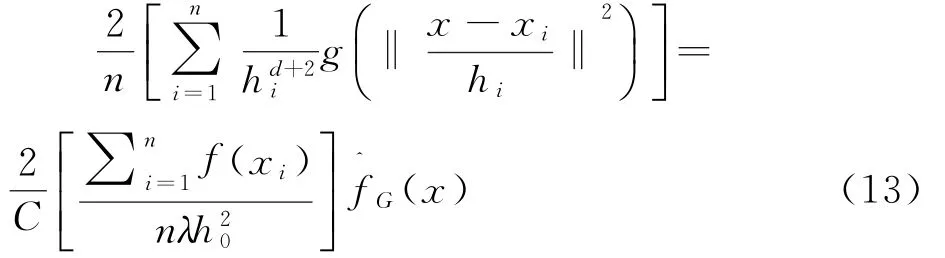
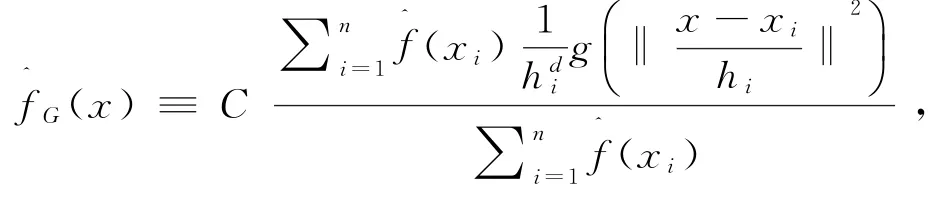
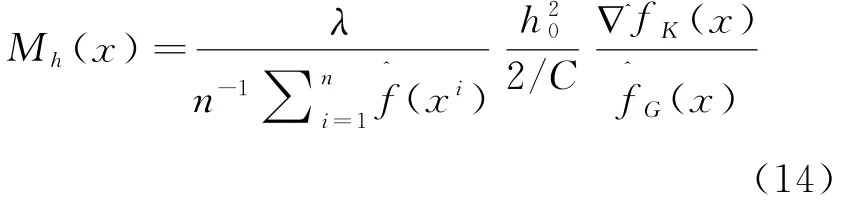
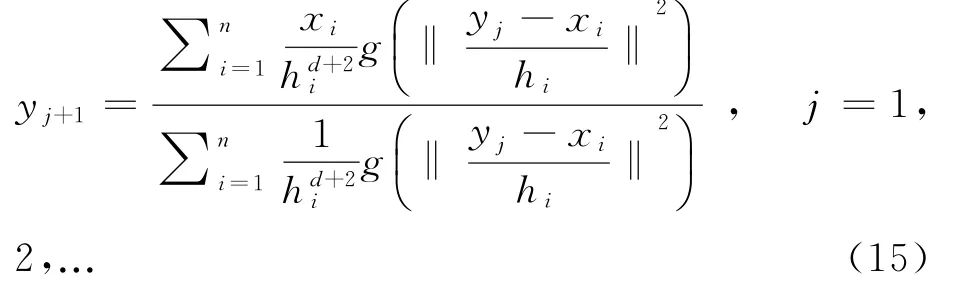
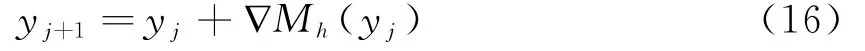
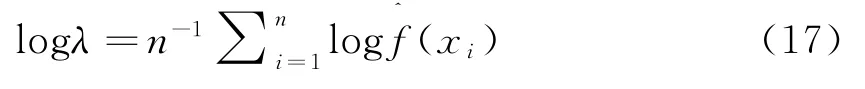
4 实验结果与分析
4.1 实验数据

4.2 实验结果与分析
5 结论

