主应力方向对软岩隧道稳定性影响的试验研究

代　聪,何　川,夏舞阳,李世琦

(西南交通大学交通隧道工程教育部重点实验室,四川 成都 610031)

隧道开挖将引起洞周围岩的应力重分布,当应力超过围岩强度或导致围岩过度变形时,隧道将面临失稳的风险.应力重分布是否导致隧道失稳主要取决于初始地应力的量值大小和分布特征,因此初始地应力是影响隧道稳定性的最重要的基本因素之一[1-4].

最大水平主应力与隧道轴线之间的位置关系对高地应力场软岩隧道围岩稳定性的影响尤为显著.因此,现有规范对高地应力区地下洞室轴线选择有明确规定.《公路隧道设计细则》规定[5]:对高地应力地区隧道的设计应避免隧道洞壁受最大主应力的作用,减小洞壁的切向应力.《水工隧洞设计规范》则规定[6]:对于高地应力场隧洞而言,宜使隧洞轴线与最大水平主地应力方向平行,或使二者之间的夹角尽量小.

由于成因复杂,初始地应力场的空间分布是很不均匀的.因此,对于超大埋深特长公路隧道而言,很难保证洞室轴线始终与最大水平主应力方向保持一致.所以,最大水平主应力与隧道轴线之间的位置关系一直是隧道与地下工程研究的重要课题.范秋雁[7]运用理论分析的方法得到了巷道应沿最大水平主应力方向开挖的结论.戚蓝等[8]在对工程区地应力研究的基础上研究了地下洞室长轴向的选取,认为地下洞室长轴方向与主压应力方向尽可能形成较小夹角,并运用数值手段验证了长轴向选择的正确性.孙玉福[9]采用数值分析的方法研究了巷道轴线与最大水平主应力之间的夹角对围岩变形和应力分布的影响规律,指出应根据地应力的分布特征并结合工程区实际情况合理选择巷道轴线的方向.郑书兵[10]、陈庆发等[11]在分析了工程区初始地应力场特征的基础上,运用数值模拟、理论分析等手段,优化了巷道轴线的走向,得出了最优巷道布置方向应与最大水平主应力呈一定夹角的结论.李曼等[12]、王俊奇等[13-14]、何本国等[15]采用数值模拟、理论分析等手段研究了最大水平主应力与隧道轴线线平行和垂直条件下围岩的稳定性,认为规范中宜使洞室轴线与最大水平主应力方向平行的规定是有适用条件的.

已有的成果主要通过理论分析、数值模拟等手段研究最大水平主应力与隧道轴线之间夹角对围岩稳定性的影响,还没有采用模型试验的方法对该问题开展系统研究.鉴于此,本文采用自主研发的“隧道三维应力场模拟试验系统”开展室内模型试验,重点研究高地应力条件下最大水平主应力方向对软岩隧道围岩稳定性的影响.研究成果可对类似工程隧道轴线的布置、支护结构的设计、围岩稳定性的评判等具有重要的指导意义和应用价值.

1　工程概况

蓝家岩隧道位于阿坝州茂县境内,为 5·12 汶川地震灾后重建项目,是连接茂县和绵竹交通的控制性工程.蓝家岩隧道的设计长度为8 149 m,最大埋深处约1 780 m,属于超大埋深特长公路隧道.隧道全线穿越地层以千枚岩为主,该类岩体具有强度低、层间接触差、节理裂隙等结构面发育、遇水软化等特点,施工难度巨大.蓝家岩隧道纵断面如图1所示.

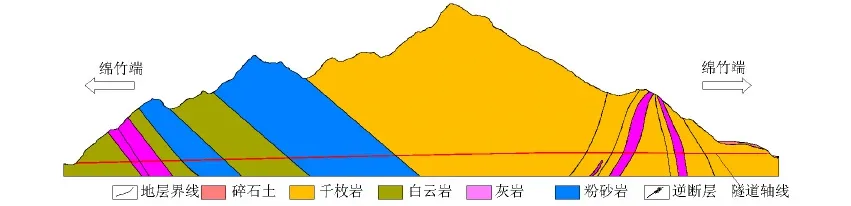
图1　蓝家岩隧道纵断面Fig.1　Longitudinal profile of Lanjiayan tunnel

蓝家岩隧道穿越 5·12 汶川地震的发震主断裂带,工程区地质构造作用强烈,褶皱和断裂极为发育,在区域构造上位于四川盆地西北部的龙门山后山推覆构造体,为韧性推覆体.地处四道沟断裂(九顶山断裂)北西侧,隧道轴线横穿盐井沟等 6条断裂和九顶山倒转向斜、疏果坪等倒转背斜[16].蓝家岩隧道区域构造如图2所示.

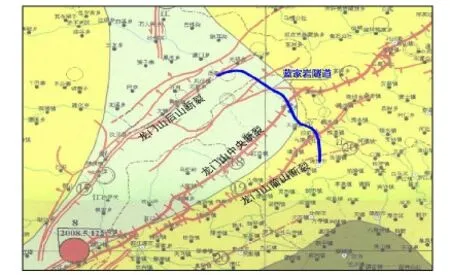
图2　蓝家岩隧道纵断面Fig.2　Regional tectonic map of Lanjiayan tunnel

本文选取Ⅴ级千枚岩高地应力软岩变形中等及严重段设计断面开展研究,隧道开挖宽度为12.52 m,高度为10.92 m,设计断面如图3所示.图中,O1、O2和O3为3圆圆心；R1、R2和R3为3圆半径.

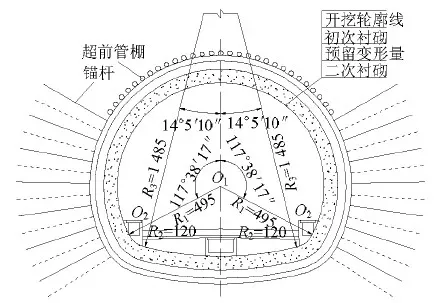
图3　隧道断面布置图Fig.3　Tunnel sectional layout design

采用水压致裂法和应力解除法开展了隧址区初始地应力场的测试工作,结果表明蓝家岩隧道工程区的初始应力场以水平构造应力为主导,且最大主应力量值大部分在20 MPa以上,属于典型的高地应力场软岩隧道.本次试验以初始地应力实测结果为基础[17],分两种工况对地应力场进行模拟:最大水平主应力与隧道轴线平行(工况1)、最大水平主应力与隧道轴线垂直(工况2),如表1所示.其中,工况1为蓝家岩隧道实测地应力状态,可知初始地应力场主应力的关系为:最大水平主应力(σH)>垂直主应力(σV)>最小水平主应力(σh),属于σHV型地应力场.

表1　初始地应力场模拟方案Tab.1　Simulation of in-situ stress field MPa

2　模型试验概况

2.1　试验系统

采用自主研发的“隧道三维应力场模拟试验系统”开展本次模型试验,该试验系统能够模拟自重应力场外,还能够模拟各种复杂构造应力场,是一个能实现应力场体三维效应的综合试验平台.其主要由2.5 m×2.5 m×1.5 m(长×高×宽)试验箱体、反力架、千斤顶和液压稳压加载装置及操作控制台等构成,如图4所示.

图4　隧道三维应力场模拟试验系统Fig.4　3D geotechnical model test system for tunnels

试验箱体能够实现前后、左右和上下3个方向的独立加载,在宽度方向上可进行0.5、1.0、1.5 m 3种尺寸的变换,从而模拟隧道的平面应变场、准三维应力场、三维应力场.反力架能够为箱体上、下、左、右4个面上的36套60 t级加载千斤顶提供反力,前、后两个面通过对拉杆连接,可为位于后面板上的9套100 t级千斤顶提供反力.液压稳压加载装置及操作控制台能够跟踪负载的变化,实现自动补偿与长期稳压.

2.2　相似关系

综合考虑到试验装置的实际情况、模型的可操作性、相对精度、边界效应对结果的影响、试验经费和时间等因素,确定试验的几何相似比CL=35，重度相似比Cγ=1.以几何相似比和重度相似比为基础,根据相似准则可得到泊松比、应变和内摩擦角物理力学参数原形值与模型值的相似比满足Cμ=Cε=Cφ=1;强度、应力、黏聚力和弹性模量的相似比满足CR=Cσ=Cc=CE=35.

2.3　相似材料

(1) 围岩

本次试验以Ⅴ级千枚岩作为原型,模型材料主要通过控制弹性模量、容重、内摩擦角和黏聚力等参数满足相似关系,以实现对原型的模拟,原型材料与模型材料的物理力学参数如表2所示.

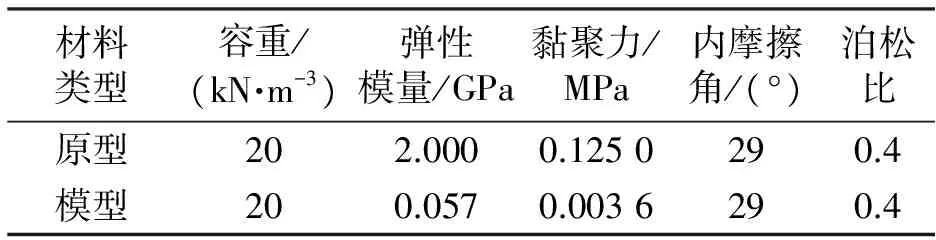
表2　原型和模型材料的力学参数Tab.2　Mechanical parameters of prototype and model materials

围岩相似材料采用一定比例的重晶石粉、粉煤灰、河沙、石英砂、凡士林、松香和机油等混合物进行模拟.将相似材料按照不同比例制成大量标准试件,采用常规三轴压力机和直剪仪等开展物理力学参数的测定试验,如图5所示.最终确定了满足物理力学参数要求的配合比,如表3所示.

(b) 直剪试验图5　围岩相似材料配比试验Fig.5　Mechanical parameters test of similar materials

表3　围岩相似材料的配比(质量比)Tab.3　Mixture ratio of similar material for rock(mass ratio)

(2) 超前管棚

试验中采用地层预加固的方法对超前管棚进行模拟[18],即提高开挖轮廓线外一定范围内的围岩参数以满足地层预加固的要求.因为试验断面在隧道拱顶部的120°范围内布置有超前管棚.所以,试验中同样在隧道拱顶部120°范围内将开挖轮廓线以外5 cm范围内的围岩参数提高一个等级,即将Ⅴ级围岩变为Ⅳ级围岩.

(3) 初期支护

在本次试验中,仅模拟隧道的初期支护.限于室内模型试验的条件,钢架、喷射混凝土和纵向连接钢筋网等难以单独模拟,故采用一定比例的水、石膏和硅藻土的混合材料来模拟初期支护.

依托工程初期支护的参数为:I20b全环钢架,间距为0.5 m;C20喷射混凝土,厚度为26 cm;φ8钢筋网,间距为20 cm×20 cm(双层).经等效计算[19],得到初期支护的等效弹性模量为31.66 GPa、等效厚度为26.27 cm.

将不同配比的特殊石膏制作成大量标准试件,通过实验测定其物理力学参数,如图6所示.该试验主要研究隧道支护结构的变形,故以弹性模量满足相似关系为准.通过实验,最终确定了满足相似关系要求的配合比：水∶石膏∶硅藻土=2.0∶1.0∶0.4.

(a)试件养护(b)压缩试验图6　初衬相似材料配比试验Fig．6　Mechanicalparameterstestofsimilarmaterials

2.4　量测系统

试验箱体的尺寸为2.5 m×2.5 m×1.5 m(长×高×宽),为监测隧道洞周位移、围岩与初衬之间的接触压力和围岩应变随开挖过程的变化规律,在隧道轴向的中间设计了1个观测断面,在监测断面的控制部位埋设了相应的监测仪器,图7为监测断面位置图.

2.4.1洞周位移

试验中主要量测隧道拱顶处的沉降及拱脚处的收敛,在各测点处预埋位移传导杆,采用差动式数显位移计在试验箱体的表面进行测量,测量精度达0.01 mm,测点布置如图8所示.

2.4.2围岩压力

采用钢弦式微型土压力盒对围岩与初衬之间的接触压力进行量测,按照设计位置预先埋入模型中,使用静态应变测试分析系统采集土压力盒的数据,测点布置如图9所示.

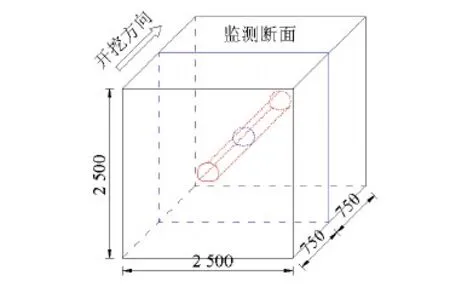
图7　模型监测断面布置Fig.7　Model monitoring section layout

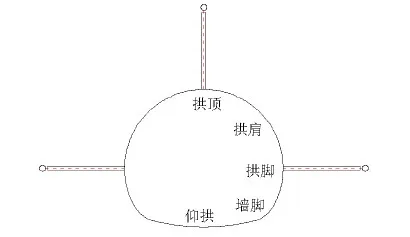
图8　洞周位移测点布置Fig.8　Test point arrangement of convergence displacement

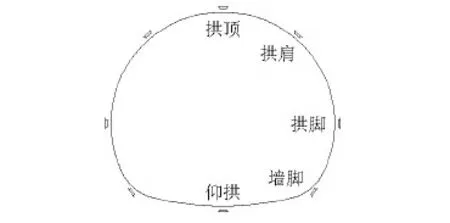
图9　围岩压力测点布置Fig.9　Test point arrangement of surrounding rock pressure

2.4.3围岩应变

采用特制的应变砖(如图10所示)监测围岩应变与应力的变化,应变砖采用围岩相似材料制作而成,在其表面粘贴三向应变花[20],按照设计位置预先埋入模型中,并严格保证应变砖与围岩材料紧密接触,应变片的应变通过静态应变测试分析系统进行采集,应变砖的测点布置如图11所示.

图10　应变砖Fig.10　Strain brick sensor

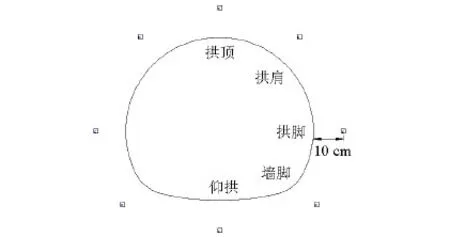
图11　围岩应变测点布置Fig.11　Test point arrangement of surrounding rock strain

2.5　模型的制作与开挖

2.5.1模型制作

本次试验采用“先加载,后开挖”的方式进行,采用填注压实的方法制作隧道模型,其具体流程为:(1) 根据围岩材料的配比大量配置模型土体;(2) 在试验箱体内从下向上逐层摊铺模型土体;(3) 采用人工对模型土体进行逐层夯实;(4) 按设计位置在监测断面处埋设测量仪器;(5) 继续填注模型土体并夯实直至模型顶部.模型的制作过程如图12所示.

(a)材料搅拌(b)材料装填(c)模型夯实(d)仪器埋设图12　隧道模型制作过程Fig．12　Makingprocessoftunnelmodel

2.5.2模型加载

试验过程中,通过加载操作台控制千斤顶在试验箱体各侧面施加不同的荷载以模拟表1所示的两种地应力工况.千斤顶的设计出力与实际地应力之间的换算过程如下:

(1) 计算地应力模型值为

(1)

(2) 计算每个加载板上的集中力为

F=σHmA;

(2)

(3) 计算每个千斤顶所需提供的集中力为

(3)

(4) 计算每个千斤顶的设计出力为

(4)

式(1)～(4)中:σHp为最大水平主应力的原型值;A为加载板的面积;n为每个加载板上千斤顶的个数;AJ为千斤顶油缸的面积.

计算得到两种工况下各方向千斤顶的出力如表4所示.试验过程中,3个方向的千斤顶根据设计出力按比例分级轮流加载,每施加一级荷载需静置一段时间,直到应力在模型内部完全传递调整平衡后,再进行其他方向下一级荷载的施加.液压千斤顶的加载如图13所示.

表4　液压千斤顶的设计出力Tab.4　Design output of hydraulic jack MPa

图13　液压千斤顶加载图片Fig.13　Hydraulic jack loading photos

2.5.3模型开挖

模型开挖采用上下台阶法,每一步的开挖进尺为10 cm (对应实际工程3.5 m),上台阶长度为20 cm (对应实际长度7.0 m),共需开挖30步,如图14 所示.

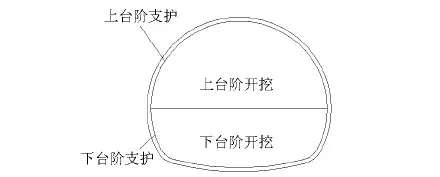
图14　隧道开挖示意Fig.14　Schematic diagram of the tunnel excavation

模型开挖与支护由人工采用特制工具完成,利用全站仪等测量仪器辅助开挖从而保证隧道的走向,隧道模型开挖照片如图15所示.

图15　隧道模型开挖Fig.15　Tunnel model excavation

2.5.4模型测试

模型开挖过程中,采用多种测量仪器开展测试工作.其中,应变砖及微型土压力盒采用TST3826F动静态应变测试分析系统进行测量,洞周位移采用差动式位移计进行测量,如图16所示.

图16　位移及应变量测系统Fig.16　Displacement and strain measurement system

3　模型试验结果的分析

隧道模型开挖、支护和测试完成后,对试验结果进行了统计分析,并根据相似准则及试验相似比,将隧道模型测得的洞周位移、围岩压力及围岩应变等结果转换为隧道原型的洞周位移、围岩压力及围岩应变.

3.1　洞周位移

利用位移计监测拱顶沉降和拱脚收敛随开挖步序的变化规律,如图17、18所示.由图17、18可知,两种工况下监测断面处洞周位移的变化规律基本一致.

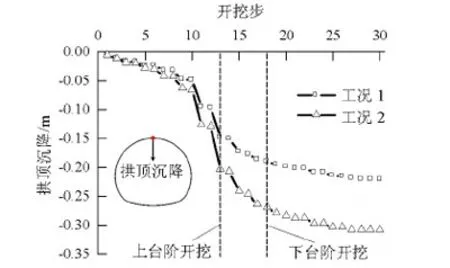
图17　拱顶沉降随开挖步的变化曲线Fig.17　Vault displacement curves with excavation step

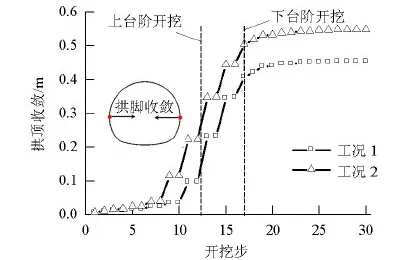
图18　拱脚收敛随开挖步的变化曲线Fig.18　Convergence curve of arch foot with excavation step

3.1.1拱顶沉降

由图17可知:掌子面到达监测断面之前,拱顶沉降已经发生,工况1的拱顶前期沉降量约占沉降量最终稳定值的43%左右,工况2的拱顶前期沉降量约占最终沉降量的40%左右;在掌子面后方,随着开挖步的推进,拱顶沉降的速率逐渐减小,最终趋于收敛;最大水平主应力与隧道轴线之间夹角对拱顶沉降影响显著,工况1、2拱顶沉降的最终值分别为-0.221 、-0.309 m.由此可知，最大水平主应力与隧道轴线平行更利于控制拱顶沉降.

3.1.2拱脚收敛

由图18可知:掌子面到达监测断面之前,拱脚收敛已经发生,工况1的拱脚前期收敛量约占最终收敛量的21%左右,工况2的拱脚前期收敛量约占最终收敛量的40%左右;在掌子面后方,随着开挖步的推进,拱脚收敛的速率逐渐减小,最终趋于稳定;最大水平主应力方向对拱脚收敛影响显著,工况1、2拱脚收敛的最终值分别为-0.454 、-0.548 m.由此可知,最大水平主应力与隧道轴线平行更利于控制拱脚收敛.

对比图17、18可知:工况1拱顶处的径向位移(-0.221 m)与拱脚处的径向位移(-0.227 m)差距不大,说明隧道拱部变形比较均匀,原因是隧道横断面上竖向地应力(16.40 MPa)与水平地应力(13.26 MPa)相差不大,应力较为均匀;工况2拱顶处的径向位移(-0.309 m)与拱脚处的径向位移(-0.274 m)差距较大,说明隧道拱部变形不均匀性增大,原因是隧道横断面上竖向地应力(16.40 MPa)与水平地应力(22.05 MPa)相差较大,导致拱顶处出现应力集中现象,使得围岩屈服变形较为严重.

3.2　围岩压力

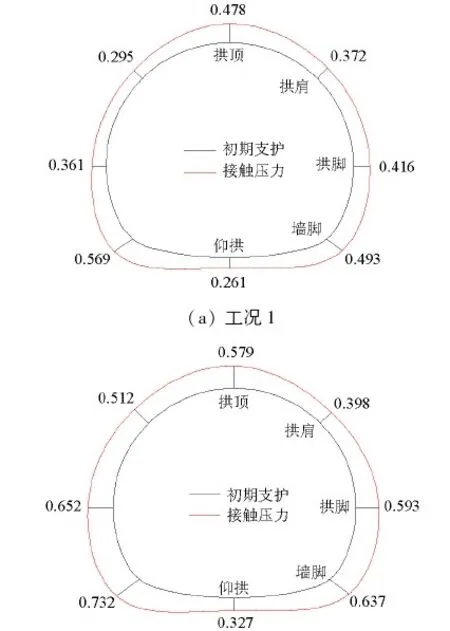
在隧道洞周预埋试验用微型土压力盒用以量测初期支护与围岩之间的径向接触压力,结果如图19 所示.

(b) 工况2图19　初期支护与围岩之间的径向接触压力(单位:MPa)Fig.19　Radial contact pressure between the primary support and surrounding rock (unit:MPa)

由图19可知:工况1与工况2各测点初期支护与围岩之间的径向力均为压力,说明隧道开挖导致围岩向洞内产生挤压;两种工况下,各测点围岩压力的量值均大于规范荷载,依托工程Ⅴ级围岩中深埋隧道的垂直压力为0.252 MPa,水平压力为0.075～0.126 MPa,说明高地应力场对围岩压力影响显著,在衬砌设计及工法选择时应引起注意;工况2各测点初期支护与围岩之间的径向接触压力均大于工况1;两种工况下,初期支护与围岩之间的径向接触压力的最大值均出现在墙脚处,最小值均出现在仰拱处;工况1拱脚处的围岩压力小于拱顶处的围岩压力,工况2拱脚处的围岩压力则大于拱顶处的围岩压力.

3.3　围岩应变

试验过程中,在隧道洞周预埋应变砖,用以监测隧道开挖引起的洞周围岩的应变增量.依据应变砖记录结果,通过坐标转换得到了各观测点的径向和切向围岩应变增量,结果如图20所示.图中,3 737.09 表示3 737.09 με，其余数据同理；正值表示拉应变增量;负值表示压应变增量；ε为应变.

由图20可知，两种工况下洞周围岩的径向应变增量均为拉应变增量,切向应变增量均为压应变增量.即隧道开挖使得围岩向洞内产生松动变形,导致洞周围岩径向应力减小,切向应力集中.

两种工况洞周围岩应变增量在空间分布和量值大小上存在明显差异:最大水平主应力与隧道轴线平行时,由于在隧道横断面上竖向地应力(16.4 MPa)大于水平地应力(13.26 MPa),导致拱脚处的围岩应变增量小于拱顶和仰拱处的围岩应变增量;最大水平主应力与隧道轴线垂直时,由于在隧道横断面上竖向地应力(16.4 MPa)小于水平地应力(22.05 MPa),使得拱脚处的围岩应变增量大于拱顶和仰拱处的围岩应变增量;工况1拱脚处的应变增量小于工况2的,而工况1 拱顶处的应变增量则大于工况2的,两种工况拱肩和墙脚处的应变增量在量值上较为接近.

(b) 工况2图20　开挖引起的洞周围岩应变增量Fig.20　Strain increment of surrounding rock caused by tunnel excavation

4　结　论

本文以蓝家岩超大埋深特长公路隧道为依托,采用自主研制的“隧道三维应力场模拟试验系统”开展了室内模型试验,研究了特定高地应力场条件下最大水平主应力方向对软岩隧道围岩稳定性的影响规律,得到了如下结论:

(1) 在σHV型高地应力场条件下,最大水平主应力与隧道轴线平行时,洞周围岩的拱顶沉降、拱脚收敛的量值比最大水平主应力与隧道轴线垂直时要小.

(2) 两种工况下,初期支护与围岩之间的接触压力量值均大于规范值,围岩压力的最大值均出现在墙脚处,最小值均出现在仰拱处;最大水平主应力方向对围岩压力影响显著,工况2各测点的围岩压力均大于工况1,且工况1拱顶处的围岩压力大于拱脚处的围岩压力,工况2拱顶处的围岩压力则小于拱脚处的围岩压力.

(3) 两种工况下,围岩的径向应变增量均为拉应变增量,切向应变增量均为压应变增量,说明隧道开挖使得围岩向洞内产生松动变形,导致洞周围岩径向应力减小,切向应力集中;在隧道横断面上,工况1拱脚处的围岩应变增量小于拱顶和仰拱处的围岩应变增量,工况2拱脚处的围岩应变增量大于拱顶和仰拱处的围岩应变增量;工况1拱脚处的应变增量小于工况2拱脚处的应变增量,而工况1拱顶处的应变增量则大于工况2拱顶处的应变增量.

参考文献:

[1]赵旭峰,王春苗,孔祥利.深部软岩隧道施工性态时空效应分析[J].岩石力学与工程学报,2007,26(2):404-409.

ZHAO Xufeng,WANG Chunmiao,KONG Xiangli.Analysis of time-space effects of construction behavior of deep soft rock tunnel[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(2):404-409.

[2]朱维申,何满潮.复杂条件下围岩稳定性与岩体动态施工力学[M].北京:科学出版社,1995:5-7.

[3]朱以文,黄克戬,李伟.地应力对地下洞室开挖的塑性区影响研究[J].岩石力学与工程学报,2004,23(8):1344-1348.

ZHU Yiwen,HUANG Kejian,LI Wei.Study on effect of in-situ stress on plastic region induced by excavation of underground openings[J].Chinese Journal of Rock Mechanics and Engineering,2004,23(8):1344-1348.

[4]张德华,刘士海,任少强.基于围岩-支护特征理论的高地应力软岩隧道初期支护选型研究[J].土木工程学报,2015,48(1):139-148.

ZHANG Dehua,LIU Shihai,REN Shaoqiang.Research on selection of preliminary support for tunnel in high ground-stress soft rock based on surrounding rock-support characteristic curve theory[J].China Civil Engineering Journal,2015,48(1):139-148.

[5]中华人民共和国行业标准编写组.JTG/T D70—2010公路隧道设计细则[S].北京:人民交通出版社,2010.

[6]中华人民共和国行业标准编写组.DL/J 5195—2004水工隧洞设计规范[S].北京:中国电力出版社,2004.

[7]范秋雁.选择巷道合理开挖方向的力学分析[J].煤炭学报,1990,15(3):62-71.

FAN Qiuyan.Mechanical analysis for choosing optimal orientation of underground opening[J].Journal of China Coal Society,1990,15(3):62-71.

[8]戚蓝,马启超.在地应力场分析的基础上探讨地下洞室长轴向选取和围岩稳定性[J].岩石力学与工程学报,2000,19(增刊1):1120-1123.

QI Lan,MA Qichao.On the selection of longitudinal direction and stability of underground opening based on the analysis of in-situ stress field[J].Chinese Journal of Rock Mechanics and Engineering,2000,19(Sup.1):1120-1123.

[9]孙玉福.水平应力对巷道围岩稳定性的影响[J].煤炭学报,2010,35(6):891-895.

SUN Yufu.Affects of in-situ horizontal stress on stability of surrounding rock roadway[J].Journal of China Coal Society,2010,35(6):891-895.

[10]郑书兵.寺河煤矿三维地应力场分布和巷道布置优化[J].煤炭学报,2010,35(5):717-722.

ZHENG Shubing.3D geostress field distribution and roadway layout optimization in Sihe mine[J].Journal of China Coal Society,2010,35(5):717-722.

[11]陈庆发,周永亮,安佳丽.复杂裂隙岩体环境下巷道轴线走向优化研究[J].岩石力学与工程学报,2014,33(增刊1):2735-2742.

CHEN Qingfa,ZHOU Yongliang,AN Jiali.Study of optimization for axis strike of roadway under environment of complex fractured rock mass[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(Sup.1):2735-2742.

[12]李曼,马平,孙强.洞室轴线走向与初始地应力关系对围岩稳定性的影响[J].铁道建筑,2011(7):70-72.

LI Man,MA Ping,SUN Qiang.The influence of the relationship between the cavity axis direction and initial stress to surrounding rocks stability[J].Railway Engineering,2011(7):70-72.

[13]王俊奇,颜月霞.地应力对洞室轴线布置影响的二维数值分析[J].长江科学院院报,2009,26(7):33-39.

WANG Junqi,YAN Yuexia.2-D numerical analysis on influence of in-situ stress on tunnel axis orientation[J].Journal of Yangtze River Scientific Research Institute,2009,26(7):33-39.

[14]王俊奇,何本国,张有天,等.深埋隧道轴线合理布置与衬砌结构稳定性研究[J].工程力学,2015,32(12):188-197.

WANG Junqi,HE Benguo,ZHANG Youtian,et al.Study on the axis orientation and stability of linings for deep tunnels[J].Engineering Mechanical,2015,32(12):188-197.

[15]何本国,张志强,何川,等.构造应力场中的软岩客运专线双线隧道稳定性研究[J].岩土力学,2012,33(5):1535-1541.

HE Benguo,ZHANG Zhiqiang,HE Chuan,et al.Study of stability of two-lane soft rock tunnel for high-speed passenger railway in tectonic geo-stress[J].Rock and Soil Mechanics,2012,33(5):1535-1541.

[16]中国地震局地壳应力研究所.四川省绵茂公路蓝家岩隧道水压致裂应力测量报告[R].北京:中国地震局地壳应力研究所,2011.

[17]四川省交通运输厅公路规划勘察设计研究院.绵竹至茂县公路(茂县段)蓝家岩隧道A标段蓝家岩隧道地应力测试报告[R].成都:四川省交通运输厅公路规划勘察设计研究院,2015.

[18]何川,佘健.高速公路隧道维修与加固[M].北京:人民交通出版社,2006:69-71.

[19]ORESTE P P.A numerical approach to the hyperstatic reaction method for the dimensioning of tunnel supports[J].Tunnelling and Underground Space Technology,2007,22(2):185-205.

[20]王汉鹏,李术才,郑学芬,等.地质力学模型试验新技术研究进展及工程应用[J].岩石力学与工程学报,2009,28(增刊1):2765-2771.

WANG Hanpeng,LI Shucai,ZHENG Xuefen,et al.Geomechanical model test new technology research development and its engineering application[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(Sup.1):2765-2771.