大跨翘曲屋盖风压分布的风洞试验与数值模拟

林拥军,沈艳忱,李明水,罗　楠

(1.西南交通大学土木工程学院,四川 成都 610031; 2.南京水利科学研究院,江苏 南京 210029)

随着社会不断进步,大跨屋盖结构已广泛应用于试验大厅、展览馆、航空港、体育馆、车站等公共建筑中,且多采用整体受力性能好的曲面结构,曲面形式对风压分布影响很大,不同的曲面形式可能会有不同的风压分布规律[1-3].除此之外,这些大跨度屋盖结构还具有质量轻、柔性大、自振频率低的特点,对风荷载十分敏感,屋盖的绕流和空气动力作用较为复杂[4-6].其中,大跨度翘曲屋盖结构造型独特优美,但目前还没有可供参考的风荷载体型系数,主要通过风洞试验来确定.

目前国内外研究者对大跨结构风荷载的研究主要有基于现场实测、风洞试验和数值模拟3种方法,现场实测由于需要耗费大量的人力、物力,因此很少采用[7],因此对结构风荷载的研究主要还是采用风洞试验和数值模拟方法.

随着计算机软硬件水平的飞速进步以及流体力学理论的发展,计算流体动力学(computational fluid dynamics,CFD)方法在结构风工程中已有所应用[8-10].Gloria等[11]对复杂建筑进行了平均风压的数值模拟,王振华[8]和KIM[12]等还分别采用基于雷诺时均方程的标准k-ε、RNGk-ε、可实现的(realizable)k-ε和雷诺应力模型(Reynolds stress model,RSM) 4种湍流模型对大跨屋盖表面平均风压分布进行了数值模拟,结果表明4种模型的模拟结果差异不大.虽然CFD方法和网格技术等还有许多需要改进之处,但是与传统风洞试验相比,CFD方法不仅可以建立建筑原型尺度,而且还可以根据研究需要,方便地改变流场和结构的相关参数,对研究对象进行全方位多层次分析,从而避免风洞试验的不足,且周期短、成本低,已逐渐成为结构风工程领域的研究热点和预测建筑物风荷载较为有效的方法[13-16].

本文以某大跨翘曲屋盖试验厅作为研究对象,首先介绍了风洞试验,并分析了屋盖风压分布及门窗开启状态的影响,然后利用流体力学分析软件CFX,采用RNGk-ε模型,通过选用较为合理的参数设定,对其进行CFD数值模拟,并将数值模拟结果与风洞试验结果进行对比分析,验证了数值方法模拟计算大跨翘曲屋盖结构平均风压分布的适用性.

1　风洞试验

1.1　工程概况

某试验厅为大跨翘曲屋盖结构,造型独特,结构平面为方形,主跨为150.0 m,高为33.6 m,该建筑中部凹曲,向两侧具有不同高度的翘曲,结构体系复杂,图1为其结构示意图,50年重现期基本风压值为0.45 kN/m2,100年重现期基本风压值为0.50 kN/m2,《建筑结构荷载规范》(GB50009—2012)对于这种造型独特的大跨度屋盖结构的风荷载计算缺乏准确的体型系数规定,也无参考资料可借鉴,为确保结构的抗风安全,应采用风洞试验,研究作用于建筑物上的风荷载,为结构设计提供依据.

1.2　试验设备

试验在西南交通大学风工程试验研究中心XNJD-3回流式低速风洞进行[17],该风洞试验段长为36 m,宽为22.5 m,高为4.5 m,试验风速范围为1.0～16.5 m/s.风洞配备了模拟大气边界层的装置,风洞底壁设有可转动360°的转盘,以变换试验的风向角.采用美国Scanvalve电子扫描阀进行测压,Dantec热线风速仪进行风速测量.

1.3　试验模型及测点

采用刚性模型,综合考虑结构几何尺寸和风洞试验段尺寸,模型的几何缩尺比为 1∶75,由金属管材、复合材料、有机玻璃等制成.在屋盖自身表面、雨棚的上下表面布置测压点,测试风压分布.根据屋盖外形特征及风向需要进行测点布置,在屋盖边缘、拐角位置及大挑檐等部位测点要密些,其他部位要疏一些.823个测点布置在建筑表面区域,50个测点布置在门面及雨棚上下表面,图2为测点布置的基本情况.

图1　某试验厅屋盖结构(单位:m)Fig.1　Roof structure of an experimental hall (unit:m)

图2　测点布置情况Fig.2　Arrangement of measuring points

1.4　试验方案

根据《建筑结构荷载规范》(GB50009—2012),当重现期为100年时,该建筑物所在地的基本风压为0.5 kN/m2,基本风速V0=28.6 m/s.所在地地貌为A类,边界层粗糙度指数为0.12,风剖面及湍流度分布由档板、尖塔、粗糙元模拟(图3).

图3　风洞试验模型Fig.3　Wind tunnel test model

试验参考点屋盖顶面风速为8 m/s,每个测点采样时间为60 s,采样频率为200 Hz.所有压力测点的脉动压力时程将同步获得.为了解门窗开启状态对结构抗风的影响,试验分为5种情况:WC-Ⅰ,门窗全部关闭;WC-Ⅱ,开一侧门和窗;WC-Ⅲ,开两侧门关窗;WC-Ⅳ,关门开一边窗;WC-Ⅴ,关门开两边窗.窗开启时的情况如图4所示.

门窗全部关闭时,试验风向按24个罗盘方向设置,隔15°设置一个试验风向,如图5所示.其余情况试验风向按8个罗盘方向设置,隔45°设置一个试验风向.每风向重复测量2次,所有压力测点的脉动压力时程同步获得.

图4　窗开启时的试验模型Fig.4　Test model of window opening

图5　试验风向示意Fig.5　Test wind direction

1.5　试验结果及分析

1.5.1屋盖风压分布

图6给出了门窗全部关闭时,屋脊线风压系数(Cp)随风向角的变化曲线,各曲线代表的是屋脊线上不同测点位置.

由图6可知:在各方向角下,屋面风压分布以吸力为主,和文献[7-8]的结论基本一致,说明大跨屋盖结构具有较为相似的风压分布特性;在凹曲方向,迎风面风压大于背风面;最大平均负风压系数为-1.350,发生在风向角为270°时来流侧屋面檐口的A1-1点;最大平均正风压系数为0.089,发生在风向角为150°时来流侧屋面顶部的A1-10点;在翘曲方向,较大平均负风压系数分别为-0.949、-0.949、-1.028和-1.029,发生在风向角分别为45°、135°、225°和315°时屋面顶部的A3-11点;最大平均正风压系数为0.298,发生在风向角为180°时来流侧屋面檐口的A14-9点.

根据体型系数的定义,风洞试验所得到的大跨翘曲屋盖各分区体型系数在-1.3～0.6之间,这一结果比《建筑结构荷载规范》(GB50009—2012)对拱形屋面规定的-0.8～-0.5要大很多,说明翘曲屋盖所受风力作用比拱形屋面更复杂,主要原因可能是屋面檐口区域脱落的旋涡使得该区域产生了较大的吸力,并提高了该处的分离强度,导致负压绝对值增大,为安全起见,大跨翘曲屋盖屋面部分的风荷载体型系数建议取不大于-1.3[8-9].

1.5.2门窗开启对风压分布的影响

为了解门窗开启状态对屋盖风压分布特性的影响,分别选取屋盖檐口中部测点A1-1、檐口角部测点A25-3以及屋盖顶部中央测点A1-7进行分析,在不同风向角下风压系数的对比结果如图7所示.由图7可知,门窗的开启对试验厅屋盖外风压系数影响较小,仅对开启位置附近的测点风压系数有一定影响,除一侧门窗开启时,270°方向角上风压系数变化较大之外,整个屋盖上表面风压系数变化并不大.

不同风向角下内压随门窗开启状态的变化情况如图8所示.

图7　门窗开启状态对风压特性的影响Fig.7　Influence of open status of windows and doors on wind pressure characteristics

图8　不同风向角下内压随门窗开启状态的变化情况Fig.8　Internal pressure varying according to open status of doors and windows and wind direction

由图8可知:门窗的开启对试验厅的内压有一定影响,不开门窗时,内压接近于0;开一边门或一边窗,当正吹时,出现较小正压,最大为0.087 MPa,屋盖受到向上的升力,应予以注意;两边同时开启时,内压为负值,屋盖受到向下的吸力,偏于安全[17].

2　数值模拟

2.1　控制方程

在建筑结构领域中所涉及到的低速流动空气是具有剪切应力的牛顿流体,近地面风的马赫数一般比较小,可看作不可压缩流体,其基本控制方程为时均形式的连续方程和动量方程[7,13]如式(1)、(2).

(1)

(2)

式中:ρ为空气密度;

μi、μj为时均速度;

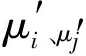
xi、xj为时均位移;

p为时均压强;

μ为湍动黏度.

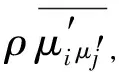
2.2　计算域、网格及边界条件

根据该建筑物的实际尺寸:150 m(长)×140 m(宽)×33.69 m(高),结合计算条件,将计算域取为1 600 m×1 600 m×800 m,阻塞比足以满足模拟建筑物所处大气环境的要求.由于该建筑物外形复杂,采用Solidwork软件构建其实体模型,使用流体力学网格划分软件Ansys Icem CFD进行部分非结构四面体网格划分,然后输入到流体力学分析软件CFX中进行求解.

为了准确模拟屋面风压分布,在网格划分时,建筑物表面及其附近采用加密网格,往外网格尺寸逐渐增大,共划分体网格2 884 882个,计算域网格划分情况如图9所示.

图9　计算域网格划分Fig.9　Mesh grid of computational domain

入口边界条件:采用速度入口模拟A类大气边界层风剖面,数值模拟采用的平均风速剖面与风洞试验平均风速剖面接近.平均风速V1=V10(z/10)α,其中:离地面10 m高度处的平均风速V10=25 m/s;粗糙度指数α=0.12;z为距离地面的高度.

来流湍流特性通过直接给定的湍流动能k和湍流耗散率ε得出[18-19].

k=0.5(VzIz)2,

(3)

ε=0.093/4k3/2/l,

(4)

式中:Iz为湍流强度,参考日本规范[8],Iz=0.1×(z/300)-α-0.05;

l为湍流积分尺度,l=100(z/30)0.5.

出口边界条件:采用完全发展出流边界条件,即流场任意物理量沿出口法向梯度为0.在计算域顶部和两侧采用对称边界条件来等价黏性流动中的无滑移壁面.在建筑物表面和地面采用无滑移的壁面条件.

2.3　计算参数

风工程的数值模拟中涉及到湍流模式的假定,较为广泛的湍流模型是二方程模型,诸如标准k-ε模型、RNGk-ε模型、Wilcoxk-ω模型、SSTk-ω模型等[10].RNGk-ε模型由于引入了主流时均应变率,可以反映涡流的非各向同性性质[20-21],较其他模型有更好的计算精度,特别是在钝体绕流的模拟中,可实现比标准k-ε模型更高的精度[22],因此本文采用RNGk-ε模型.针对该模型在雷诺数Re较低时适用性降低的情况,在计算时与非平衡壁面函数结合使用[1].

为保证计算的稳定性,并获得较高的计算精度,对流项的离散选用了具有三阶精度的二次迎风插值格式,速度压力耦合采用SIMPLEC算法,迭代计算的收敛标准设为无量纲均方根残差降至10-5以下,且表面风压基本保持不变时,即认为流场进入稳态[9].

2.4　计算结果分析

图10为门窗全部关闭(WC-Ⅰ)时,风洞试验和数值模拟计算得到的屋面风压系数等值线情况.

从图10中可以看出:0°风向角下,屋盖最大风压系数发生在第1屋盖翘曲两侧边缘处,计算风压系数为-1.27,与风洞试验最大负风压系数测点A2-4位置较为接近,试验最大负风压系数为-1.06;90°风向角下,屋盖最大风压系数发生在来流方向第2屋盖翘曲边缘处,计算风压系数为-1.24,与风洞试验最大负风压系数测点A3-17的位置较为接近,试验最大负风压系数为-1.54;0°和90°风向角下,迎风面均为压力,而背风面、两侧和屋盖大部分为吸力,90°风向角下风压分布的数值模拟结果稍大于风洞试验结果,而0°风向角下风压分布的数值模拟结果与风洞试验结果吻合较好.

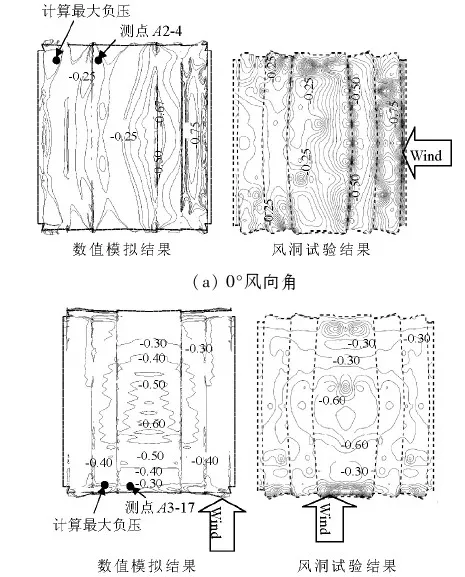
(b) 90°风向角图10　风压系数等值线(单位:MPa)Fig.10　Wind pressure coefficient contour (unit:MPa)

图11为0°和90°风向时,10 m高度处水平风速矢量图.

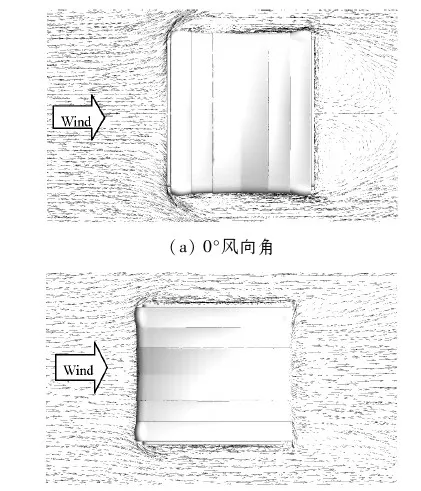
(b) 90°风向角图11　不同风向时10 m高度处水平风速矢量图Fig.11　Vectorgraph of horizontal wind speed at 10 m height for different wind directions

从图11中可以看出:0°和90°风向来流在迎风屋面处均未发生流动分离,也没有强的旋涡;在0°风向时,风流绕过建筑后,在侧面伴随着分离和漩涡产生,在背风面形成了两个较大且对称的尾涡;90°风向时,侧面和背风面分离和漩涡均不如0°风向明显.

图12为0°风向时,翘曲向屋脊线竖剖面风速矢量图,从图12中可以看出:风流在翘曲的边缘有较大的分离,且翘曲表面有较强的漩涡产生,说明这种翘曲屋盖所受风力比普通大跨度屋盖复杂得多[2].

图13为0°风向角下,凹曲和翘曲方向屋脊线的风压系数.

图12　0°风向时翘曲向屋脊线竖剖面风速矢量图Fig.12　Wind speed vectorgraph of vertical cut plane of warpage roof ridge for 0° wind

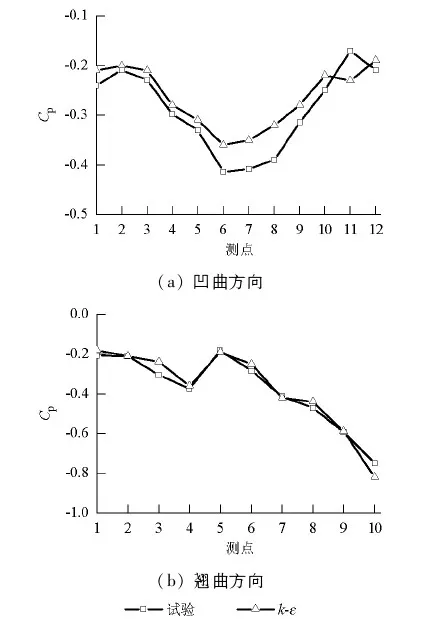
图13　0°风向角屋脊线上风压系数Fig.13　Wind pressure coefficient of roof ridge for 0° wind

从图13中可以看出,由于风洞试验采用的是缩尺模型,而数值方法采用的是全尺模拟,数值模拟网格划分质量、计算参数的设定以及试验模型缩尺等原因,数值模拟值与试验值之间存在一定的差别[8],但差别不大,且变化趋势一致,表明采用RNGk-ε模型模拟计算大跨度翘曲屋盖平均风压分布具有较好的计算精度.

综上所述,风荷载作用下,由于风流在屋盖翘曲的边缘有较大的分离,且在翘曲表面有较强的漩涡产生,其受风力比普通大跨度屋盖复杂得多,对风荷载作用也更为敏感.风荷载是结构设计的主要控制荷载,无论是主体结构风荷载计算,还是附属构件的设计,务必予以足够的重视.同时,由于翘曲边缘的流动分离作用,大跨翘曲屋盖结构中,风荷载最不利的位置在翘曲边缘和屋面顶部区域,局部风压系数较大,无论是结构整体设计还是局部构件设计,翘曲边缘和屋面顶部区域应予以重点注意.

3　结　论

通过对大跨翘曲屋盖结构风荷载试验数据进行分析,以及采用RNGk-ε模型进行CFD数值模拟,并将数值模拟结果与风洞试验结果进行对比分析,主要结论如下:

(1) 门窗的开启对大跨翘曲屋盖外风压系数影响较小,对内压有一定影响,开一边门窗时,屋盖会受到向上的升力,两边同时开启时,内压对屋盖有向下的吸力作用.

(2)采用RNGk-ε模型模拟计算大跨度翘曲屋盖平均风压分布具有较好的计算精度,来流方向为翘曲向(0°风向)时,风流绕过建筑后,在来流方向建筑两侧会伴随着分离和漩涡产生,且在背风面会形成大的对称尾涡,而来流方向为凹曲向(90°风向)时,侧面和背风面分离和漩涡不明显.

(3) 风流在翘曲的边缘有较大的分离,在翘曲表面有较强的漩涡产生,其受风力比普通大跨度屋盖复杂,对风荷载作用也更敏感.

(4) 大跨翘曲屋盖在各方向角下,屋面风压分布以吸力为主,风荷载最不利位置在翘曲边缘和屋面顶部区域,无论是结构整体设计还是局部构件设计,翘曲边缘和屋面顶部区域都应予以重点注意.

参考文献:

[1]楼文娟,孙斌,卢旦,等.复杂型体悬挑屋盖风荷载风洞试验与数值模拟[J].建筑结构学报,2007,28(1):107-112.

LOU Wenjuan,SUN Bin,LU Dan,et al.Wind tunnel tests and numerical simulation of wind loads on complex cantilevered roofs[J].Journal of Building Structures,2007,28(1):107-112.

[2]林拥军,宋长江,罗楠,等.大跨度单层网壳结构风洞试验研究[J].工业建筑,2013,43(7):130-134.

LIN Yongjun,SONG Changjiang,LUO Nan,et al.Study on wind tunnel tests of large-span single-layer reticulated shell structure[J].Industrial Construction,2013,43(7):130-134.

[3]马文勇,刘庆宽,尉耀元.具有凹面外形的大跨屋盖结构风荷载分布及风洞试验研究[J].振动与冲击,2013,31(22):34-38.

MA Wenyong,LIU Qingkuan,WEI Yaoyuan.Wind load distribution and wind tunnel tests for a curved concave long-span roof[J].Journal of Vibration and Shock,2013,31(22):34-38.

[4]罗楠,廖海黎,李明水.大跨屋盖结构共振响应的简化CQC 法[J].西南交通大学学报,2012,47(6):915-921.

LUO Nan,LIAO Haili,LI Mingshui.Simplified CQC method for resonant response of long-Span roof structure[J].Journal of Southwest Jiaotong University,2012,47(6):915-921.

[5]黄鹏,蔡玢,全涌,等.基于实测的低矮房屋屋面风压极值计算方法[J].西南交通大学学报,2014,49(2):247-253.

HUANG Peng,CAI Bin,QUAN Yong,et al.Peak pressure estimation method of wind loads on low-rise building based on field measurement[J].Journal of Southwest Jiaotong University,2014,49(2):247-253.

[6]UEMATSU Y,WATANABE K,SASAKI A,et al.Wind induced dynamic response and result ant load estimation of a circular flat roof[J].Journal of Wind Engineering & Industrial Aerodynamics,1999,83:251-261.

[7]傅继阳,赵若红,徐安,等.大跨屋盖结构风效应的风洞试验与原型实测研究[J].湖南大学学报:自然科学版,2010,37(9):12-18.

FU Jiyang,ZHAO Ruohong,XU An,et al.Wind tunnel and full scale study of wind effects on a large roof structure[J].Journal of Hunan University:Natural Sciences,2010,37(9):12-18.

[8]王振华,袁行飞,董石麟.大跨度椭球屋盖结构风压分布的风洞试验和数值模拟[J].浙江大学学报:工学版 ,2007,41(9):1462-1466.

WANG Zhenhua,YUAN Xingfei,DONG Shilin.Wind tunnel experiment and numerical simulation of wind pressure distribution of long span ellipsoidal shell structure[J].Journal of Zhejiang University:Engineering Science,2007,41(9):1462-1466.

[9]顾明,赵雅丽,黄强,等.低层房屋屋面平均风压的风洞试验和数值模拟[J].空气动力学学报,2010,28(1):82-87.

GU Ming,ZHAO Yali,HUANG Qiang,et al.Wind tunnel tests and numerical simulation of mean wind pressures on roof of low-rise buildings[J].Acta Aerodynamica Sinica,2010,28(1):82-87.

[10]MURAKAMI S.Current status and future trends in computational wind engineering[J].Wind Eng.Indus.Aerodyn,1997,67/68:3-34

[11]GLORIA M,MORET R A,PEDRO M.Experimental and numerical study of wind pressures on irregular plan shapes[J].Journal of Wind Engineering and Industrial Aerodynamics,2005,93:741-756.

[12]KIM S E,FERIT B.Application of CFD to environment flows[J].Journal of Wind Engineering and Industrial Aerodynamics,1999,81:145-158.

[13]GOSMAN A.Developents in CFD for industrial and environmental applications in wind engineering[J].Journal of Wind Engineering and Industrial Aerodynamics,1999(81):21-39

[14]日本建筑学会.建筑风荷载流体计算指南[M].北京:中国建筑工业出版社,2010:19-33

[15]黄本才,汪丛军.结构抗风分析原理及应用[M].上海:同济大学出版社,2008:125-159.

[16]王福军.计算流体动力学分析——CFD 软件原理与应用[M ].北京:清华大学出版社,2004:18-23.

[17]林拥军,罗楠,丁巍,等.某试验厅风洞试验研究报告[R].成都:西南交通大学风工程试验研究中心,2013.

[18]马骏,周岱,李华锋等.大跨度空间结构抗风分析的 数值风洞方法[J].工程力学,2007,24(7):77-85.

MA Jun,ZHOU Dai,LI Huafeng,et al.Numerical wind tunnel technique for the wind resistance analysis of long span spatial structures[J].Engineering Mechanics,2007,24(7):77-85.

[19]林郁,卓新.开敞式叉筒网壳风场数值模拟与受力分析[J].浙江大学学报:工学版,2004,38(9):1170-1174.

LIN Yu,ZHUO Xin.Numerical simulation and mechanics analysis of wind loading on open latticed groined barrel vault[J].Journal of Zhejiang University:Engineering Science,2004,38(9):1170-1174.

[20]YAKHOT V,ORSZAG S A,THANGAM S.Development of turbulence models for shear flows by a double expansion technique[J].Physics of Fluids A,1991,4(7):1510-1520.

[21]SPECIAL C G,THANGAM S.Analysis of an RNG based turbulence model for separated flows[J].International Journal of Engineering Science,1992,10:1379-1388.

[22]KASPERSKI M,NIEMANN H J.The LRC (load response correlation) method:a general method of estimating unfavorable wind load distributions for linear and nonlinear structural behavior[J].Journal of Wind Engineering and Industrial Aerodynamics,1992,43(3):1753-1763.