上柔下刚混合结构动力放大效应简化计算研究
熊海贝,陈 琳,吴 颖,贾国成
(同济大学土木工程学院,上海 200092)
上柔下刚混合结构是由上下两种不同材料和结构体系组成的复合结构,通常整体结构的质量、刚度在上部与下部结构分界处产生突变,其动力反应与竖向规则体系不同,容易产生“鞭梢效应”,如轻木-混凝土结构、轻木-砖混结构、钢-砖混结构、钢-混凝土结构等.
针对该类结构,美国规范UBC97[1]指出,当结构的下上两部分抗侧刚度比不小于10,且整体结构的自振周期不大于上部结构自振周期的1.1倍时,下部结构与上部结构可单独计算地震作用.欧洲规范[2]规定,沿高度不规则的结构采用简化的振型方法(国内称为振型分解法)进行分析.我国《建筑抗震设计规范》[3]建议竖向不规则结构采用振型分解反应谱法或时程分析法.上海市《轻型木结构建筑技术规程》[4]规定,当底层平均抗侧刚度与相邻上部木结构的平均抗侧刚度之比大于10时,上部木结构和下部结构可单独计算,上部木结构的水平地震作用按轻型木结构计算,并应乘以放大系数;当刚度比为10时,放大系数取2.0,当刚度比为40时,放大系数取1.5,中间采用线性插值.
文献[5]基于不同抗侧刚度比的轻木-混凝土上下混合结构模型的振动台试验,通过分析得出:对于刚度比大于8的结构,当结构整体的一阶自振周期不大于上部结构周期的1.1倍时,上部结构可作为独立结构进行计算,但水平地震影响系数应放大,对于不同刚度比的影响,放大系数建议取1.5~2.5.文献[6]对不同刚度比的轻木-混凝土上下混合结构进行有限元分析,得出当刚度比小于10时,采用整体底部剪力法;当刚度比大于10时,采用上部和下部结构单独计算的方法,并对上部木结构乘以放大系数,放大系数的取值与刚度比有关.
文献[7]以振型分解反应谱法和结构振动理论为基础,通过算例分析加层部分刚度、质量等对结构地震作用的影响,探讨了下刚上柔轻型门式刚架加层结构的地震作用规律.文献[8]以振型分解反应谱法和底部剪力法为基础,总结了下刚上柔多层砌体房屋地震作用的规律并从理论和算例两方面加以证明.
文献[9]对胶合木框架剪力墙与混凝土框架的竖向混合结构进行了低周反复荷载试验,对比分析木结构放在地面上与放在混凝土框架上的破坏形态、受力机理以及极限承载力、弹性抗侧刚度、耗能能力等结构性能.文献[10]在对混合结构动力分析中采用分开构造的矩阵,简化了广义阻尼比来近似表征上部钢结构和下部混凝土结构不同阻尼耗能特性的影响.
文献[11]对于一个一层的混凝土框架木楼盖混合结构模型进行了水平单向弹性加载试验和往复加载破坏试验.结果表明:木楼盖在弹性受力范围有良好的平面内刚度,当混合结构达到塑性时,木楼盖具有较高的水平承载力.文献[12]以轻木-混凝土混合结构振动台试验的实测数据为基础,运用非线性加权最小二乘法、有理分式多项式法和随机减量法3种方法识别结构阻尼,得出在不同刚度、质量和加速度幅值的情况下结构阻尼的取值范围.
文献[13]提出了一种以钢筋混凝土剪力墙结构为主要抗侧力体系,在跃层住宅单元内使用木结构的新型高层住宅.并以某跃层住宅楼为例,对比分析了新型结构和原混凝土结构的受力性能.结果表明新型轻木-混凝土跃层住宅是一种更为绿色环保的结构体系,能有效减小建筑物在地震作用下的响应.
已有的规范与研究成果指出当下上刚度比大于某一数值时,混合结构上下部分可单独计算地震力,并对上部结构乘以放大系数.基于此,本文考虑到结构的地震力是由刚度比、质量比共同决定,在提出刚度质量综合比概念的基础上,给出了一个混合结构动力放大效应简化计算方法,并采用振动台试验和振型分解法进行验证,为更方便地设计计算上柔下刚混合结构提供参考.
1 动力放大效应简化计算方法
针对上柔下刚混合结构,本文提出的动力放大效应简化计算方法的基本思路为将整体结构(图1[14])等效为两质点结构体系(图2),下部结构等效为质点1,其质量、刚度分别为下部结构的等效质量m1eq、等效刚度k1eq,上部结构等效为质点2,其质量、刚度分别为上部结构的等效质量m2eq、等效刚度k2eq,采用振型分解反应谱法计算顶部质点的地震力,其相对于直接坐落在基础上的质点地震力比值,即为放大系数.

图1 西雅图Marselle公寓Fig.1 Marselle apartment in seattle
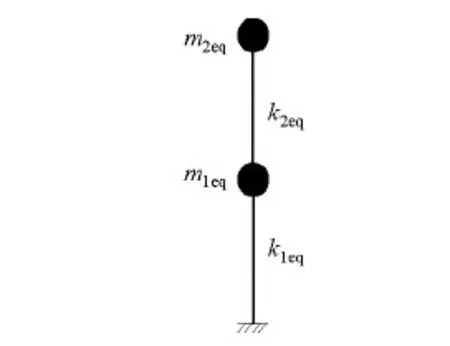
图2 两质点体系振动力学模型Fig.2 Vibration mechanical model of two-particle system
1.1 计算假定
混合结构动力放大效应简化计算方法采用以下基本假定:
(1) 上部结构的阻尼比与下部结构的阻尼比相等,即ξ1=ξ2;
(2) 结构的计算方法采用振型分解反应谱法;
(3) 地震影响系数取值采用中国抗震规范规定的地震影响系数曲线;
(4) 等效质量系数的取值,对于单质点体系,取1;对于多质点体系,按中国抗震规范规定统一取0.85.
1.2 动力放大系数计算公式
根据动力放大效应简化计算方法的基本思路,参考底部剪力法,将等效质量定义为
(1)
根据自振圆频率与刚度、质量的关系,可得等效刚度:
keq=4meqπ2/T2,
(2)
式(2)中的基本周期T采用能量法[15]计算:
(3)
式(1)~(3)中:mi为结构各质点的质量;n为结构层数;χ为等效质量系数;Gi为结构各质点的重力荷载;ui为将各质点的重力荷载Gi视为水平力作用在质点i处产生的水平位移.
底部与顶部质点的刚度质量综合比β定义为
(4)
(5)
(6)
结构质量比定义为
em=m2eq/(m1eq+m2eq).
(7)
结构刚度比定义为
ek=k1eq/k2eq.
(8)
根据两质点体系的自由振动方程
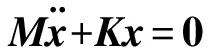
(9)
可得
(10)
式中:ω0为结构的自振圆频率.
第1振型向量为(1,x2),其中:
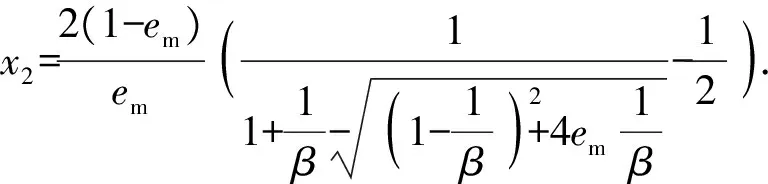
(11)
当仅考虑第1振型时,由振型分解反应谱法可得顶部质点的地震力为
F2=γ1x2α1G2eq,
(12)
式中:γ1和α1分别为第1振型的参与系数和地震影响系数;G2eq为顶部质点的等效重力荷载.
当m1和m2的地震影响系数相等时,顶部质点的地震力相对于直接坐落在基础上的质点的地震力的放大系数为
(13)
2 简化计算方法的验证
2.1 采用振动台试验验证
选取1组公开发表的振动台试验数据[5],利用简化计算方法进行对比分析,从而验证使用该方法计算上柔下刚混合结构动力放大效应的有效性和可靠性.文献[5]给出了5个不同抗侧刚度比的底部1层混凝土结构、上部2层轻型木结构的轻木-混凝土混合结构模型(“1+2”体系).模型的平面尺寸为6.1 m×3.7 m,底部混凝土结构层高为3.0 m,柱截面为270 mm×270 mm,纵向梁截面为200 mm×300 mm,横向梁截面为250 mm×250 mm,混凝土板厚为80 mm;上部轻型木结构层高均为2.8 m,楼面搁栅由纵向剪力墙承重,屋面结构由双坡轻型木桁架覆盖屋面板构成.
现选取模型4与模型6在0.1g地震水准作用下的试验结果与简化计算法结果进行对比,本次试验中的0.1g地震水准作用近似地相当于8度(0.3g)多遇地震作用.模型4与模型6的质量、刚度分布见表1,k1、k2、k3和m1、m2、m3分别为模型一层、二层、三层的刚度和质量,由简化计算法与试验得到的上部木结构动力放大系数对比见表2.从表2可以看出,简化计算法得到的放大系数与试验结果的比值最大为1.15,误差均在15.00%以内.两者吻合较好,验证了该方法可用于计算上部结构动力放大效应.

表1 模型质量、刚度分布Tab.1 Mass and stiffness distribution based on the model

表2 放大系数对比Tab.2 Comparison of amplified coefficients
2.2 采用振型分解法验证
为验证放大系数简化计算方法是否适用于求解混合结构动力放大效应,以轻木-混凝土结构为例,采用振型分解法得到的二层层间剪力与仅考虑上部结构的底部剪力法得到的基底剪力比值作为振型分解法解,与式(13)计算得到的简化计算法解对比分析.假定结构处于8度区(地震加速度为0.20g),Ⅳ类场地第1组,结构阻尼比为0.05.
2.2.1二层结构
选取二层轻木-混凝土结构进行验证,底层为混凝土结构,二层为轻型木结构(“1+1”体系).底层与二层质量分别为10.5、3.5 t,二层刚度为4 kN/mm,底层刚度为自变量(案例1),简化计算法与振型分解法结果对比见图3.

图3 放大系数对比(案例1)Fig.3 Comparison of amplified coefficients (case 1)
从图3可知:当β=1时,η达到最大值;当β相同时,简化计算法结果小于振型分解法;随着β的增大,误差先增大再减少,β=1时,误差达到最大值,为5.13%.
2.2.2三层结构
选取三层轻木-混凝土结构(底层为混凝土结构,二、三层为轻型木结构,即“1+2”体系)进行验证,顶部两层仅考虑第1振型的振动,并将其等效为单质点,等效质量系数取0.85.第i(i=1,2,…)层刚度和质量分别为ki和mi.
当k2=k3=4 kN/mm,m1=10.5 t,m2=m3=3.5 t (案例2)时,简化计算法与振型分解法结果对比见图4.从图4可知:当β=1时,η达到最大值;当β相同时,简化计算法结果小于振型分解法;两者的误差均在15.00%以内,最终趋于收敛.
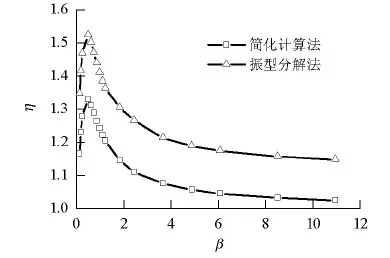
图4 放大系数对比(案例2)Fig.4 Comparison of amplified coefficients (case 2)
当k2=4 kN/mm,k3=2 kN/mm,m1=22.5 t,m2=3.5 t,m3=1.1 t (案例3)时,放大系数对比见图5;当k2=4 kN/mm,k3=2 kN/mm,m1=10.5 t,m2=3.5 t,m3=1.1 t (案例4),放大系数对比见图6.从图5、6可知:当β=1时,η达到最大值;当β相同时,简化计算法结果小于振型分解法;两者的误差小于20.00%,最终趋于收敛.

图5 放大系数对比(案例3)Fig.5 Comparison of amplified coefficients (case 3)
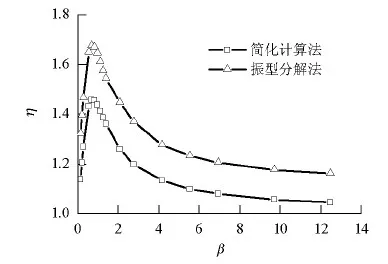
图6 放大系数对比(案例4)Fig.6 Comparison of amplified coefficients (case 4)
2.2.3六层结构
以六层轻木-混凝土结构为例,验证简化计算方法的有效性,结构底部两层为混凝土结构,其它层为轻型木结构(“2+4”体系).简化计算方法将整体结构等效为两质点体系,底部质点与顶部质点仅考虑第1振型的振动,等效质量系数取0.85,且始终保持k1与k2相等.
当k3=k4=k5=k6=4 kN/mm,m1=m2=10.5 t,m3=m4=m5=m6=3.5 t (案例5),简化计算法与振型分解法结果对比见图7.从图7可知:当β相等时,简化计算法结果小于振型分解法;两者的误差小于15.00%,最终趋于收敛.
当k3=k4=k5=4 kN/mm,k6=2 kN/mm,m1=m2=22.5 t,m3=m4=m5=3.5 t,m6=1.1 t (案例6),放大系数对比见图8;当k3=k4=k5=4 kN/mm,k6=2 kN/mm,m1=m2=10.5 t,m3=m4=m5=3.5 t,m6=1.1 t (案例7),放大系数对比见图9.从图8、9可知:当β=1时,η达到最大值;当β相等时,简化计算法结果小于振型分解法;两者的误差均在20.00%以内,最终趋于收敛.
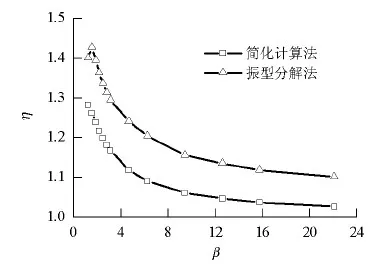
图7 放大系数对比(案例5)Fig.7 Comparison of amplified coefficients (case 5)

图8 放大系数对比(案例6)Fig.8 Comparison of amplified coefficients (case 6)
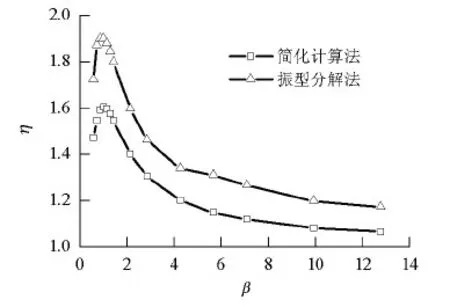
图9 放大 系数对比(案例7)Fig.9 Comparison of amplified coefficients (case 7)
由上可得,η简化计算法与振型分解法结果吻合较好(误差20.00%左右),放大效应简化计算方法可用于六层结构,且等效质量系数取0.85.
3 参数分析
由放大系数公式(13)可以看出,上部结构的动力放大效应仅与整体结构自身的质量、刚度的分布有关,因此分析质量比、刚度质量综合比、刚度比对放大系数的影响.
3.1 质量比、刚度质量综合比
考虑3个刚度质量综合比(0.5、1.0、2.5),相应地由简化计算法得到的η-em变化如图10(a)所示.可知,当β一定,随着em的增大,η减小.
考虑3个em(0.15、0.20、0.25),其η-β曲线如图10(b)所示,可知,当em相同,随着β的增大,η先增大后减小,当β为1时,η达到最大值.

图10 质量比和刚度质量综合比参数分析Fig.10 Parametric analysis of the mass and stiffness mass integrated ratios
3.2 刚度比
以轻木-混凝土“1+1”体系、“1+2”体系、“2+4”体系为例,η-ek曲线如图11,可以看到,η随着ek的增大,先近似线性增加,后非线性减小;减小速率随ek增大而降低,逐渐趋于稳定;随着结构层数的增加,η的峰值先增大后减小.
当上下两个质点的振动耦连关系开始减弱时(从振型向量可以看出),下上刚度比的比值可定义为采用放大系数计算上部结构动力放大效应的分界点.由简化计算法得到的顶部质点一阶振型水平位移随刚度比的变化见图12.对于二层结构,当刚度比不小于5,顶部质点位移的拟合直线为x2=0.95ek-1.07;对于三层结构,当刚度比不小于7,顶部质点位移的拟合直线为x2=0.88ek-2.55;对于六层结构,当刚度比不小于6时,顶部质点位移的拟合直线x2=0.93ek-1.64.可近似认为,当刚度比小于7时,随着刚度比的增加,顶点位移非线性增加,当刚度比不小于7时,顶部质点位移线性增加,而线性直线段的斜率大于非线性曲线段.
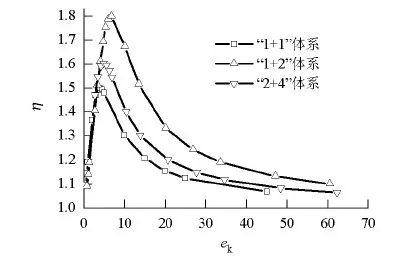
图11 刚度比参数分析Fig.11 Parametric analysis of the stiffness ratio

图12 顶部质点一阶振型水平位移-刚度比曲线Fig.12 Horizontal displacement-stiffness ratio curves of upper patical
4 结 论
(1) 在考虑刚度比、质量比对混合结构地震力影响的基础上,提出了刚度质量综合比的概念,给出了混合结构动力放大效应简化计算方法.
(2) 采用1组公开发表的振动台试验数据对简化计算法进行验证,两者符合较好(误差20.00%以内);以轻木-混凝土二层结构(“1+1”体系)、三层结构(“1+2”体系)、六层结构(“2+4”体系)为例,采用振型分解法对简化计算法进行验证,两者均符合较好(误差小于20.00%).从而验证了使用简化计算方法计算上柔下刚混合结构动力放大效应的有效性和可靠性.
(3) 参数分析表明,当刚度质量综合比一定,随着质量比的增大,放大系数减小;当质量比相同,随着刚度质量综合比的增大,放大系数先增大后减小,当刚度质量综合比为1时,放大系数达到最大值;此外,本文建议当结构下上刚度比不小于7时,可采用简化计算法计算上部结构的动力放大效应.
参考文献:
[1]International Council of Building Officials (ICBO) Uniform Building Code 1997[S].Washington D.C.:International Conference of Building Official, 1997.
[2]European Committee for Standardization.EN 1998 Eurocode 8:design of structures for earthquake resistance,2006[S].Brussels: European Committee for Standardization,2006.
[3]中国建筑科学研究院.GB50011—2010 建筑抗震设计规范[S].北京:中国建筑工业出版社,2010.
[4]上海现代建筑设计(集团)有限公司.DG/TJ08-2059—2009 轻型木结构建筑技术规程[S].上海:上海市建筑建材业市场管理总站,2009.
[5]熊海贝,倪春,吕西林,等.三层轻木-混凝土混合结构足尺模型模拟地震振动台试验研究[J].地震工程与工程振动,2008,28(1):91-98.
XIONG Haibei,NI Chun,LÜ Xilin,et al.Shaking table tests on 3-storey wood-concrete hybrid structure[J].Journal of Earthquake Engineer and Engineer Vabration,2008,28(1):91-98.
[6]何敏娟,李英俏.刚度比对轻木-混凝土上下混合结构地震作用响应的影响[J].特种结构,2013,30(2):54-58.
HE Minjuan,LI Yingqiao.Effects of the Stiffness ratio on earthquake response of wood-concrete structures mixed up and down[J].Special Structure,2013,30(2):54-58.
[7]吕凤伟,曹双寅.下刚上柔轻型门式刚架加层结构地震作用规律探讨[J].钢结构,2008,23(9):37-39.
LÜ Fengwei,CAO Shuangyin.Discussions on the seismic response rules of soft-upper-rigid-down structures added with light-gauge steel portal frames[J].Steel Structure,2008,23(9):37-39.
[8]赵福顺,赵玉星.下刚上柔多层砌体房屋地震作用的讨论[C]∥第八届全国结构工程学术会议论文集(第Ⅲ卷).昆明:[出版者不详],1999:910-914.
[9]王瑄.木-混凝土竖向混合结构抗侧力性能试验研究[D].南京:南京工业大学,2015.
[10]鲁晨.阻尼比在上柔下刚结构中的简化计算方法[J].新材料新装饰·建筑技术,2013(12):364-365.
LU Chen.Simplified calculation method of damping ratio in soft-upper-rigid-down structures[J].New Material New Decoration,2013(12):364-365.
[11]李硕.混凝土与木混合结构抗侧力试验[J].建筑结构,2013,43(增刊1):732-735.
LI Shuo.Test of one storey hybrid structure with concrete frame and timber floor under lateral load[J].Building Structure Supplement,2013, 43(Sup.1):732-735.
[12]林凡伟,熊海贝.轻木-混凝土混合结构振动台试验阻尼识别研究[D].上海:同济大学,2008.
[13]熊海贝,许鸿盛,陈佳炜.轻木-混凝土跃层住宅抗震性能分析[J].结构工程师,2017,33 (1):85-92.
XIONG Haibei,XU Hongsheng,CHEN Jiawei.Seismic performance of light wood-concrete structure for duplex apartment building[J].Structural Engineers,2017,33(1):85-92.
[14]KARACABEYLI E,CONROY L.Technical guide for the design and construction of tall wood buildings in Canada[M].[S.l.]:FPInnovations,2014:98-112.
[15]李国强,李杰,陈素文,等.建筑结构抗震设计[M].北京:中国建筑工业出版社,2014: 219-220 .

