千米级混合梁斜拉桥双目标控制施工监控体系

谢明志,杨永清,卜一之,赵灿晖,张克跃,王学伟

(西南交通大学土木工程学院,四川 成都 610031)

混合梁斜拉桥因其在力学特性和经济指标等方面的突出优点,受到诸多国家青睐[1].在近15 a的时间里,世界前10座最大跨度斜拉桥中,该桥型已占7座,呈现由大跨度向千米级超大跨度发展的趋势[2].该体系结构面临的特点有:结构复杂、施工工艺要求高、循环施工、施工安全稳定问题突出[3-5],且因施工工艺质量引起的参数偏差对成桥线形和内力影响巨大[6-7].因此,对桥梁施工控制提出更高的要求.从基于索力和标高为主的“双控”[8]方法发展到多多罗大桥引入的“精度控制”[9],斜拉桥监控手段从传统的重视施工现场控制拓展到施工全过程控制,是监控理念、监控体系的飞跃.国内外学者在对大量工程实践研究的基础上,以构件的无应力状态量[10]为关键控制参数,深化、拓展了全过程自适应控制,成功运用于世界首座千米级全钢箱梁斜拉桥[11].

随着斜拉桥跨径的不断增大,文献[6-7,12-14]对全钢箱梁斜拉桥和大跨混合梁斜拉桥的施工及监控将面临的挑战和困难进行了探讨,对该体系桥梁结构及环境参数变化对施工期及成桥索力、塔偏、主梁线形及应力的影响,并确定主次要参数，对施工期结构安全稳定,面临的环境因素、由于材料的差异对边中跨受力的影响、计算理论方法、局部受力分析、控制策略等诸多问题开展了深入研究.国内关于千米级混合梁斜拉桥施工控制关键问题以及如何构建高效、高精度的施工控制系统的相关研究较少.因此,深入研究该复杂结构与全钢箱斜拉桥的差异并建立适用于该复杂结构的施工监控体系,确保千米级混合梁斜拉桥施工监控的高效性、高精度及安全性具有重要的理论及实践意义.

1　问题的提出

传统的“索力-标高”控制方法在600 m左右的钢斜拉桥、混凝土斜拉桥以及叠合梁斜拉桥中证实是行之有效的,且获得较好的效果[15-16].但对于千米级混合梁斜拉桥,由于跨径的增加,结构受力、施工工艺以及施工期安全稳定等各方面与常规跨径斜拉桥相比将发生巨大变化,且边中跨材料、刚度差异巨大,其局限性已愈显突出[2],将面临以下问题:

(1) 增加阶段线形评判的难度,大幅延长误差分析时间;

(2) 传统方法重视安装阶段的控制,缺少对主梁的制造线形控制,从而造成安装时理论安装标高与梁段顺接可达到的标高存在较大不吻合风险，这将对主梁线形控制及钢梁质量造成不利影响;

(3) 传统方法受环境(如温度、风荷载等)及施工临时荷载影响较大，新安梁段高程以设计温度下精匹配的高程为控制参数,监控指令中的索力是基于设计温度下的索力,施工现场环境温度的变化、临时荷载的改变将造成拉索二张索力、精匹配安装标高均难以控制,加大了后期拉索的调整工作量.

本文以鄂东长江公路大桥(大陆首座千米级混合梁斜拉桥,主桥跨径为3×67.5 m+72.5 m+926.0 m+72.5 m+3×67.5 m)为依托(如图1),基于几何控制理论[11,17],研究其施工控制问题,建立高效率、高精度、安全可靠的施工监控理论及体系,为复杂体系的施工控制建立实施原则及控制系统框架.

图1　鄂东大桥总体布置图(单位:m)Fig.1　General layout of Edong Bridge (unit:m)

2　施工监控体系的建立

2.1　基于几何控制的双目标控制

由几何控制的基本思想、理论可知,对于超大跨度混合梁桥施工控制,在无误差、理想情况下,可对构件无应力参数实施控制,主梁、拉索和索塔以成桥阶段对应的无应力构形进行制造加工及浇筑,安装及张拉阶段重现其无应力构形,保证初始无应力参数与成桥阶段一致,达到控制斜拉桥几何构形和内力状态的目的.基于此构思,可将桥梁监控过程对测试误差的物理量控制转化为测量误差较小的几何量控制,从而实现控制目标.

超大跨度混合梁斜拉桥以构件的初始几何尺寸为控制对象,以对其恢复作为制造、安装全过程控制的依据,此为监控实施基础之一;钢梁与混凝土梁结构行为差异明显是施工控制面临的巨大挑战之一,混凝土梁的线形容错性较好,内力和应力容错性较差,呈现于钢梁相反的特性[2],选择单一控制指标难以实现设计意图,应对边中跨采取不同的控制目标及策略,此为监控实施基础之二;边中跨结构由于材料、刚度的差异,将导致误差出现的几率及影响大大不同,且考虑混凝土收缩徐变的影响,若单纯以设计成桥索长进行控制,混凝土梁应力、钢主梁线形将与设计理想状态存在无法容忍的误差,此为监控实施基础之三.考虑上述因素及施工期面临的挑战等问题,客观上要求对不同材料和结构采取不同的控制策略及手段,建立不同的控制目标,这是区别“单目标几何控制法”的根本所在.

千米级混合梁斜拉桥的施工控制可归纳为:基于几何控制理论,以构件无应力状态量为控制对象,根据钢主梁和混凝土梁力学行为特点、材料、刚度的差异确定不同的控制目标和控制策略;主跨钢箱梁以几何状态量为主要目标控制参数,通过无应力索长进行调控;边跨混凝土箱梁以其力学状态量为基本目标控制参数,控制无应力线形,通过索力和索长双控进行应力调控,该方法深化并拓展了几何控制法,从“单目标几何控制”到“双目标几何控制”,为千米级混合梁斜拉桥的监控体系奠定理论基础.

2.2　施工监控体系构建

双目标几何控制法可描述为全过程自适应控制系统,可分为准备、制造、安装3个主要阶段.准备阶段主要工作为设计复核、安装计算及结构参数敏感性分析.设计复核在于进行设计校核分析,并确定无应力线形和无应力索长,计算节段制造尺寸,混凝土梁段立模标高；安装计算对设计复核阶段的计算结果进行复核,确定各阶段理想目标线形,确保结构受力安全,建立预警机制；参数敏感性分析为阶段容许误差制定、参数识别、误差修正及控制策略的制定奠定基础.制造加工阶段,通过收集相关构件制造参数,评估和确定制造过程的可靠性和正确性,分析误差产生原因,在此基础上带到安装分析模型中,由制造误差对安装过程和成桥状态的影响进行评估.该阶段是数据采集→分析评估→调控措施→模型更新修正的过程.安装阶段通过指令进行钢梁精匹配安装及拉索张拉.其控制系统如图2所示.该系统是一个参数采集、误差识别与模型修正、控制决策的过程.该控制系统的建立为复杂桥梁结构的施工控制、施工期安全性分析提供参考,推动超大跨度桥梁研究发展与应用.

2.3　有限元仿真模型

采用Midas/Civil对该桥建立有限元模型,充分考虑斜拉索垂度、梁柱、大位移等非线性效应.按照施工进程划分663个施工阶段进行全过程分析.根据无应力状态法基本原理对主跨钢箱梁悬臂施工时除了合龙段外，单悬臂钢梁单元全部一次无重激活，施工到对应节段时再将梁段自重以均布荷载形式添加;边跨混凝土梁现浇施工单元按施工流程分段无重激活,然后以均布荷载和集中荷载的形式添加节段自重.梁与过渡墩、辅助墩位置连接均为纵向活动和竖向约束.在索塔位置竖向约束,纵向采用弹性约束，过渡墩和索塔位置横向设置抗风支座约束，地质条件较好,塔底用固结处理简化.本模型主梁采用“鱼骨梁”,全桥共1 488个节点,1 685个单元,其中，梁单元1 445个,模拟主梁、索塔及桥墩，只受拉单元240个,模拟斜拉索,定义93个截面和30个变截面组.全桥有限元模型如图3所示.

图2　双目标控制系统流程Fig.2　Operation flowchart of double target control system

图3　鄂东大桥全桥有限元模型Fig.3　Finite element model of Edong bridge

3　双目标控制系统关键问题研究及验证分析

上述双目标控制系统的建立,以鄂东长江公路大桥为依托,针对结构力学行为特点、关键构件制造加工以及现场安装阶段面临的问题和挑战、施工期安全控制策略等关键问题开展研究是确保千米级混合梁斜拉桥安全建设的核心问题，也是探明该体系与全钢大跨斜拉桥等复杂结构施工控制的异同,对控制策略的制定具有重要的理论及实践意义.

3.1　超大跨度混合梁斜拉桥初始无应力状态量的确定方法

由于几何非线性及混凝土收缩徐变的影响,超大跨度混合梁斜拉桥初始无应力状态量的求解与全钢斜拉桥存在差异[15],需迭代求解.混凝土主梁初始无应力状态量的确定过程本质上是调整索力使混凝土梁应力达到设计要求,其线形则由无应力线形控制.钢主梁初始无应力状态量的确定过程是通过使无应力索长及主梁无应力线形满足要求,几何线形是控制的关键,无应力索长和无应力线形则是控制方法.考虑几何非线性及收缩徐变影响,边中跨初始无应力线形迭代求解流程如图4所示.鄂东长江公路大桥主跨制造线形即为钢梁初始无应力线形,如图5所示.中跨、边跨混凝土梁初始无应力线形可通过立模标高反应,如图6所示.因结构、受力对称,仅以南岸(黄石侧)为例.

从图5、6可看出,中跨钢主梁设计线形与制造线形有明显的区别,其本质在于二者的应力状态不同,设计线形不能作为制造线形.中跨设计线形与制造线形相差达1 m,随着施工的进展,钢主梁线形变化十分明显,如何保障主跨钢箱梁线形符合设计成桥要求是施工监控面临的一大挑战和难点.因此,中跨以几何线形作为施工监控目标具有合理性和重要现实意义;边跨混凝土箱梁最大预拱度约40 mm,与中跨相比,以应力作为控制目标具有合理性.

图4　超大跨度混合梁斜拉桥初始无应力状态量迭代求解Fig.4　Initial unstressed state amount iterative of super long-span hybrid girder cable-stayed bridge

图5　中跨钢主梁制造线形Fig.5　Fabrication profile of steel girder of middle span in south

3.2　关键构件制造、浇筑控制

“双目标控制”除了对制造阶段钢主梁、拉索及钢锚箱无应力几何参数的控制,还需加强对边跨浇筑时应力和线形的监控.通过对制造及浇筑阶段相关参数的采集,对关键构件制造参数、浇筑状况进行反馈,判断构件制造及浇筑水平,分析误差原因及是否超限,将实际制造参数带入模型进行计算更新,指导安装过程,对成桥线形及内力进行总体评估,达到自适应控制状态.钢梁南北岸制造控制成果如表1所示.

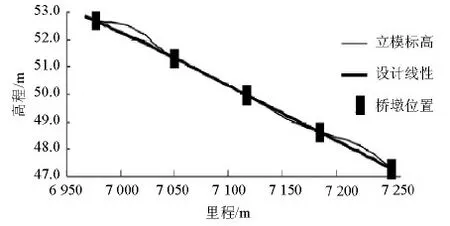
图6　边跨混凝土梁立模标高Fig.6　Formwork erection elevation of side spans in Huangshi of south

表1梁段制造成果误差
Tab.1Errors of manufacturing processmm

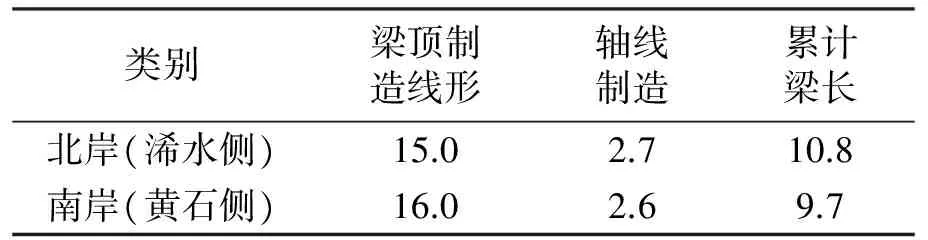
类别梁顶制造线形轴线制造累计梁长北岸(浠水侧)15．02．710．8南岸(黄石侧)16．02．69．7

为满足控制需要,需加强制造、浇筑阶段数据采集、分析,进而对安装阶段进行模型更新计算,判断后序梁段的制造以及安装过程中如何对主梁线形及内力的调整,从而达到自适应控制.其控制及调控流程如图7所示.

3.3　关键构件安装控制

根据几何控制理论的基本原理,无应力状态量为目标控制量,安装阶段是无应力状态量的重现过程.通过对关键构件制造阶段数据采集及评价,基于双目标控制总体思路,为安装控制的有效实施奠定可靠可信的基础.超大跨度混合梁斜拉桥边跨支架拆卸、拉索张拉、钢箱梁及钢锚箱的安装控制是施工监控面临的重难点问题.

鄂东大桥支架的卸除曾采用3种方案:方案1：中跨合龙后卸除;方案2：分阶段多次卸除;方案3：最大悬臂阶段,中跨合龙前卸除.3种方案分析表明,支架在合龙前、后的卸除对混凝土箱梁施工期抗裂、成桥线形方面优于分阶段卸架.当采用原主梁安装线形及无应力索长时,3种方案成桥线形差异如图8所示.对成桥线形的影响,方案1、3优于方案2.基于几何控制理论,支架卸除时间对成桥影响甚微,但考虑其与主梁连接情况较为复杂,对其卸除需考虑拆除前、后结构安全和中跨合龙施工的影响.因此,方案1、3均为可行方案.由于合龙施工时需顶推调整合龙口宽度,支架的存在将对主梁的水平移动产生约束且具有较大的不确定性,难以计算其阻力.考虑到施工安全、规避顶推风险等因素,鄂东长江公路大桥采用在合龙前卸除支架,为全过程控制提供了较强的安全保障.

图7　制造浇筑阶段控制流程Fig.7　Operation flowchart in manufacturing and cast-in-place process

图8　成桥线形差(浠水侧)Fig.8　Geometric profile difference upon completion of the bridge in Xishi side

施工误差不仅影响无应力索长,更将对成桥产生较大影响.由于混凝土锚点施工误差离散型较大且较难控制,若简单以混凝土收缩徐变迭代的无应力索长为张拉控制目标,将难以实现主梁应力和线形控制目标.安装阶段,需结合边中跨实测锚点误差、拉索批次制造误差、梁重等因素,基于设计成桥目标再次对无应力索长迭代计算,进行修正.

基于双目标几何控制法,对斜拉索的张拉控制,中跨以引伸量作为主要控制量,索力为辅;边跨则以索力控制为主,引伸量为辅的原则进行,分阶段目标实现,对无应力索长的有效控制进而达到合理的成桥内力及线形.鄂东长江公路大桥斜拉索的张拉控制如图9所示,可规避施工环境变化的影响,如温度、施工临时荷载等.

如前所述,制造加工阶段对钢锚箱及钢锚箱数据采集并进行阶段评估,为下一批次的制造及安装阶段的调控提供依据.安装阶段实则为无应力线形和无应力曲率实现的过程.通过对节段箱梁在精匹配时期将无应力线形的控制转换成夹角控制,以相对高程进行精确匹配,高效、高精度的确保中跨无应力线形.对于钢锚箱的控制,采取全过程相对安装法,通过严格控制首节钢锚箱,根据制造阶段收集的误差,将后序钢锚箱的安装以相对上一阶段的位置实施控制,从而规避环境因素的影响实现全天候的安装.安装3～5节钢锚箱后按绝对位置测量高程进行线形评价,保证安装成果满足监控要求.

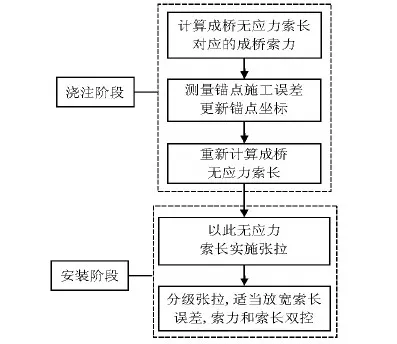
图9　超大跨度混合梁斜拉桥斜拉索控制流程Fig.9　Operation flowchart of cable control of super long-span hybrid girder cable-stayed bridge

3.4　基于双控目标控制的施工期安全控制策略

悬臂的增长,其前端负弯矩趋于增大,桥梁安全稳定问题愈显突出.大桥全过程几何、材料等非线性稳定分析表明,随着悬臂的增大,结构稳定性明显下降,安全系数降低,如图10所示.大悬臂阶段前端负弯矩是影响超大跨度混合梁斜拉桥安全的重要因素,非线性稳定系数波动,在起吊下一梁段时最小,对该阶段的控制需确保结构的稳定性.

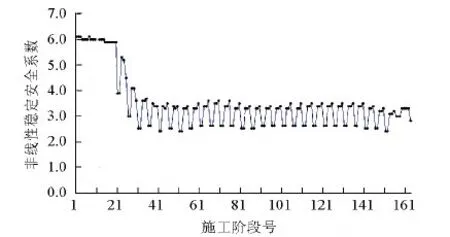
图10　施工全过程稳定安全性变化Fig.10　Stability and safety variety of whole-procedure construction

根据双目标几何控制方法,若保证成桥无应力状态量不变,只要施工结束后的结构体系及作用体系与设计成桥状态一致即能达到理想成桥线形和内力.基于此理念,鄂东长江公路大桥大悬臂阶段通过对中跨拉索引伸量的控制进行“超张拉”,待结构安全稳定性提高后再将其“放张”,与此同时,配合施加临时配重,优化施工临时荷载达到降低过程控制风险[18-19].施工期安全稳定控制方案如表2、3所示,调控后计算所得各指标符合相应规范和设计标准.同单一的调索方案相比,调索范围由12对拉索减小为9对拉索，拉索最大超张量由600 mm 减小至320 mm,最大索力由757 kN减小至649 kN,简化了施工,并且提高了拉索张拉的安全性.

表2大悬臂阶段拉索“超张”、“放张”方案
Tab.2Over tension and loosening process of cables under the longest cantilevered construction stagem

拉索编号设计二张索长调整后二张索长二张超张量放回设计索长时间中跨21#索362．423362．3800．04325号索二张完成后中跨22#索376．813376．7680．04526号索二张完成后中跨23#索391．256391．1720．08427号索二张完成后中跨24#索405．874405．7580．11628号索二张完成后中跨25#索420．480420．3170．16328号索二张完成后中跨26#索435．118434．9490．16929号索二张完成后中跨27#索449．742449．5130．22929号索二张完成后中跨28#索464．409464．1500．25930号索二张完成后中跨29#索479．140478．8720．26830号索二张完成后

表3　临时配重施加方案Tab.3　Temporary balance weight application method

3.5　施工监控体系验证分析

本文基于几何控制理论的“双目标控制”法,根据理论计算及全过程监控分析得出主梁线形及索力理论值与实测值对比，如图11～12所示.

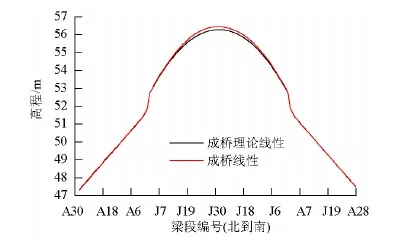
图11　成桥线形对比Fig.11　Comparison with profile upon completion of the bridge

主梁线形平顺,边跨混凝土梁最大误差为11 mm,中跨钢箱梁最大误差为157 mm,边跨斜拉索单根索力误差在 5.00%以内,中跨均在8.00%以内.大桥的建设经历了温度、临时荷载等复杂的环境变化,线形及索力误差均满足监控目标要求.对于超大跨度混合梁斜拉桥,边中跨结构形式、力学行为的差异使得误差绝对值分布明显不同,也验证了对该复杂结构需采用不同的控制策略.

限于篇幅,仅列出本桥施工控制实施效果汇总结果,如表4所示.鄂东大桥成桥阶段主梁线形、应力、成桥索力及塔偏均满足《公路斜拉桥设计细则》(JTG/T D65-01—2007)及监控手册中的控制目标要求,获得了良好的控制效果.钢箱梁线形相对误差为L/598 9,优于日本多多罗大桥的L/387 0和昂船洲大桥的L/339 3;轴线相对误差为L/470 05,塔偏相对误差为L/124 34,混凝土梁单根拉索索力最大误差为 4.50%,钢梁索力最大误差为6.30%.该系统实现全过程、高精度监控.

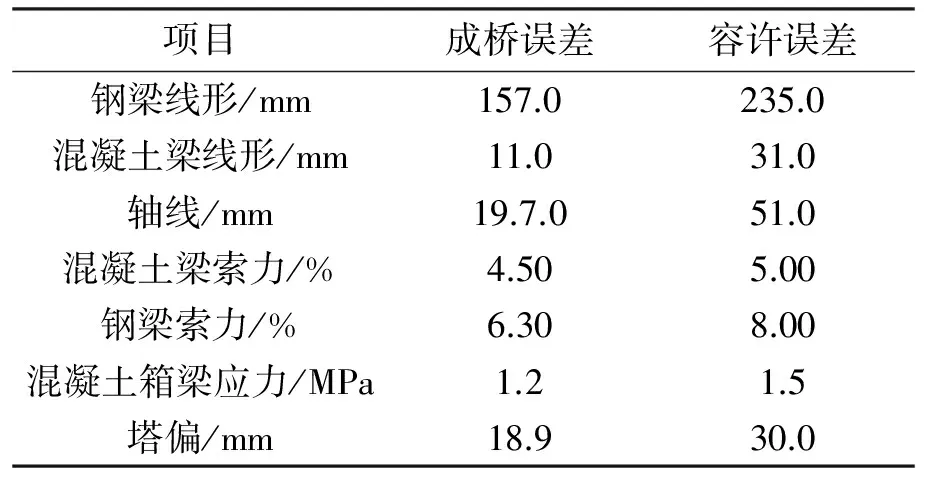
表4　监控实施效果汇总Tab.4　Summary of construction control error

注:表中为误差绝对值;索力误差指单根拉索误差.

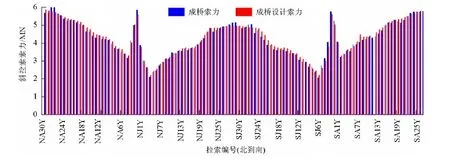
图12　成桥索力对比Fig.12　Comparison with cable force upon completion of the bridge

4　结　论

本文基于工程控制理论与方法,以大陆首座千米级混合梁斜拉桥为依托,通过理论分析、有限元数值计算,开展特大跨度混合梁斜拉桥施工全过程关键构件计算分析、安全控制等核心问题,深入研究并建立适用于该复杂结构的监控体系,得到如下结论：

(1) “双目标”几何控制体系的成功运用,推动并扩大基于几何控制的全过程自适应控体系的适用范畴,能高效、高精度的对复杂结构进行施工监控.系统的研发在理论与实践上为复杂体系的施工控制建立实施原则及控制系统框架,能自动适应各类型超大跨度斜拉桥的施工控制.

(2) 理论研究与工程实践表明,“双目标”几何控制体系可规避影响施工控制的诸多不利因素,能建立完善的安全控制体系及策略,对关键构件的计算分析及安装控制等全过程控制的开展提供高效的有力保障,进而保证结构安全、可控,内力和线形满足既定目标.

(3) 超大跨度混合梁斜拉桥制造浇筑及安装阶段的误差易导致成桥内力和线形偏离理想状态,探明误差传播机理规律、评价体系、多参数识别、误差修正理论及最优控制是实现复杂结构高质量控制的关键,是自适应控制理论的核心,也是下一阶段千米级混合梁斜拉桥全过程控制研究的重点.

参考文献:

[1]陈开利,余天庆,习刚.混合梁斜拉桥的发展与展望[J].桥梁建设,2005(2):1-4.

CHEN Kaili,YU Tianqing,XI Gang.Development and prospective of hybrid girder cable-stayed bridge[J].Bridge Construction,2005(2):1-4.

[2]徐国平,张喜刚,刘玉擎,等.混合梁斜拉桥[M].北京:人民交通出版社,2013:216-233.

[3]詹建辉,彭晓彬.大跨度组合梁斜拉桥结构设计方案研究[J].桥梁建设,2016,46(4):85-91.

ZHAN Jianhui,PENG Xiaobin.Study of structural design scheme for long span composite girder cable-stayed bridge[J].Bridge Construction,2016,46(4):85-91.

[4]赵雷,孙才志,杨兴旺.鄂东长江大桥施工过程非线性稳定性分析[J].西南交通大学学报,2012,47(5):741-747.

ZHAO Lei,SUN Caizhi,YANG Xingwang.Stability analysis of Edong Yangtze River Bridge during construction[J].Journal of Southwest Jiaotong University,2012,47(5):741-747.

[5]谢明志,卜一之,魏然,等.千米级混合梁斜拉桥无应力索长及几何线形控制[J].重庆交通大学学报:自然科学版,2013,32(3):374-378.

XIE Mingzhi,BU Yizhi,WEI Ran,et al.Unstressed cable length and geometric linear control of hybrid girder cable-stayed bridge with 1000 m sale span[J].Journal of Chongqing Jiaotong University:Natural Science,2013,32(3):374-378.

[6]宋亚洲,李昌辉,蔡瑞瑞.钢-混凝土混合梁斜拉桥参数敏感性分析与控制[J].施工技术,2013,42(23):14-16，29.

SONG Yazhou,LI Changhui,CAI Ruirui.Parameter sensitivity analysis and control of steel-concrete girder for cable-stayed bridge[J].Construction Technology,2013,42(23):14-16， 29.

[7]谢明志,卜一之,张克跃,等.特大跨度混合梁斜拉桥几何控制法参数敏感性[J].长安大学学报:自然科学版,2014,34(3):66-73.

XIE Mingzhi,BU Yizhi,ZHANG Keyue,et al.Sensitivity of parameters of super long-span hybrid girder cable-stayed bridge based on geometry control method[J].Journal of Chang’an University:Natural Science Edition,2014,34(3):66-73.

[8]石雪飞,项海帆.斜拉桥施工控制方法的分类分析[J].同济大学学报,2001,29(1):55-59.

SHI Xuefei,XIANG Haifan.Analysis of construction control systems of cable-stayed bridge[J].Journal of Tongji University,2001,29(1):55-59.

[9]MANABE Y,HIRAHARA N,MUKASA N,et al.Accuracy control on the construction of Tatara Bridge[C]∥Cable-Stayed Bridges-Past,Present and Future:Proceedings of IABSE Conference．Malmö:IABSE,1999:332-335.

[10]秦顺全.无应力状态控制法——斜拉桥安装计算的应用[J].桥梁建设,2008(2):13-16.

QIN Shunquan.Application of unstressed state control method to calculation for erection of cable-stayed bridge[J].Bridge Construction,2008(2):13 -16.

[11]李乔,卜一之,张清华.基于几何控制的全过程自适应施工控制系统研究[J].土木工程学报,2009,42(7):69-77.

LI Qiao,BU Yizhi,ZHANG Qinghua.Whole-procedure adaptive construction control system based on geometry control method[J].China Civil Engineering Journal,2009,42(7):69-77.

[12]张家元,丁望星,朱世峰.荆岳长江公路大桥索塔锚固钢锚梁结构体系分析[J].桥梁建设,2015,45(2):89-93.

ZHANG Jiayuan,DING Wangxing,ZHU Shifeng.Analysis of steel anchor beam structural system of anchorage in pylon of Jingyue Changjiang River highway bridge[J].Bridge Construction,2015,45(2):89-93.

[13]赵雷,贾少敏,顾乡.分幅斜拉桥斜拉索无应力长度的简化计算方法[J].重庆交通大学学报:自然科学版,2014,33(6):5-8，88.

ZHAO Lei,JIA Shaomin,GU Xiang.Simplified calculation method of unstressed length of cable-stayed bridge with separate twin-decks[J].Journal of Chongqing Jiaotong University:Natural Science,2014,33(6):5-8， 88.

[14]张清华,黄灿,卜一之,等.大跨度钢斜拉桥制造误差的传播及其效应特性[J].西南交通大学学报,2015,50(5):830-837.

ZHANG Qinghua,HUANG Can,BU Yizhi,et al.Fabrication error propagation properties of key components of large-span cable-stayed bridges with steel box girde[J].Journal of Southwest Jiaotong University,2015,50(5):830-837.

[15]尹子安.钢桁梁斜拉桥施工控制[D].成都：西南交通大学,2017.

[16]赵彦峰.悬拼施工的叠合梁斜拉桥线形控制与分析[D].成都：西南交通大学,2016.

[17]李乔,卜一之,张清华,等.大跨度斜拉桥施工全过程及几何控制概论与应用[M].成都:西南交通大学出版社,2009:15-26.

[18]赵灿晖,卜一之.超大跨混合梁斜拉桥施工控制技术[R].成都:西南交通大学,2011.

[19]王振海,王泽华,赵灿晖.千米级斜拉桥施工期应力调控措施研究[J].施工技术,2012,41(9):74-78.

WANG Zhenhai,WANG Zehua,ZHAO Canhui.Study on stress redeployment of cable-stayed bridge with 1 000 m scale span during construction[J].Construction Technology,2012,41(9):74-78.