低亚声速射弹垂直入水的流体与固体耦合数值计算研究

胡明勇， 张志宏， 刘巨斌， 孟庆昌

(海军工程大学 基础部， 湖北 武汉 430033)

0　引言

超空泡射弹作为一种速射防御性武器，在反鱼雷、水雷等方面具有较好的应用前景。超空泡射弹与常规射弹的主要不同之处在于采用了超空泡减阻技术。目前对超空泡射弹理论和实验研究成果主要集中于弹体在水中运动过程或低速物体的入水问题。国内对于入水问题的研究起步较晚，对于入水过程的理论及数值模拟研究始于20世纪80年代，研究的方法主要是：有限差分法[1]、边界元法[2]、光滑粒子流体动力学方法[3]、附加质量法[4]、格子波兹曼方法[5-6]、有限体积法[7-12]、实验方法[13-14]等。国外对入水问题研究的起步较早，从球体入水问题[15-16]开始研究，进而对二维结构物入水拍击问题进行数值研究[17-18]，再扩展到三维结构物入水问题[19-22]。由于弹体高速入水过程(弹体从空气中穿越空气、水交界面进入水中过程称为入水过程)时间短，空气、水、弹体之间会发生强烈的耦合作用，且激波、自由面与超空泡相互作用，并伴随着湍动、相变、可压缩等大量复杂的流动现象，研究难度大，已有的研究成果不多。

本文针对低亚声速(速度小于等于0.3倍水中声速)超空泡射弹入水问题，利用ANSYS软件构建低亚声速射弹入水问题的空气- 固体- 流体多介质耦合有限元模型，基于水的格林爱森(Gruneisen)状态方程以及空气的Linear_Polynomial状态方程，射弹模型采用拉格朗日算法，流体域采用任意拉格朗日- 欧拉有限元算法，以LS-DYNA软件为计算平台，对低亚声速射弹入水过程的空泡演化过程、射弹速度衰减规律以及入水空泡面闭合和深闭合时间进行了数值模拟，完成了低亚声速射弹入水空泡流场与弹道的多介质耦合计算，分析了射弹初始入水速度对空泡面闭合、空泡深闭合时间的影响。

1　数学模型

对超空泡射弹入水过程中的流场进行计算时，流场除了要满足连续性方程外，还必须满足质量和动量守恒方程。

1)质量守恒方程[23]

(1)

式中：Mρ、Lρ和Kρ分别为容量、转换和散度矩阵；ρ为材料密度；t为时间。

2)动量守恒方程

(2)

式中：M和L分别为广义质量和传递矩阵；vr为对应于参考构型描述下的速度；fi和fe分别为内力和外力向量。

本文中弹体与流体间的耦合采用欧拉- 拉格朗日流体与固体耦合算法。其显著特点是结构与流体的有限元模型重叠在一起，在计算中通过一定的约束方法将结构与流体相耦合，可实现力学参量的传递。此外，多物质组通过关键字*ALE_MULTI-MATERIAL_GROUP定义，结构与流体之间的耦合通过关键字*CONSTRAINED_LAGRANGE_IN_SOLID定义。进行多物质耦合计算时，单元算法采用LS-DYNA中的算法11，弹体采用黎曼- 斯蒂尔杰斯全积分六面体(S/R)单元，算法为拉格朗日算法，固体单元与流体单元之间采用无侵蚀的罚函数耦合。

2　算例

2.1　模型参数

射弹分别采用锥头圆柱体结构(见图1)，圆柱长L=50 mm，直径D=10 mm，头部圆锥角α=90°. 材料采用铝合金，密度2.7×103kg/m3. 射弹结构采用刚性材料模型MAT_RIGID.

水采用LS-DYNA提供的“无为”材料模型(MAT_NULL)和Gruneisen状态方程[24]，即

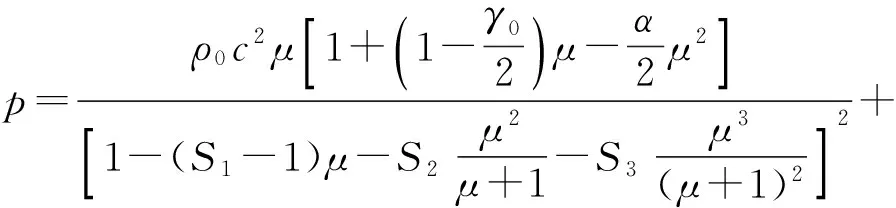
(γ0+αμ)E，

(3)

式中：p为压力；c为声速；μ=ρ/ρ0-1，ρ为水密度，ρ0为水压缩前的密度；E为单位体积内能(计算时取初始单位体积内能E0)；S1、S2、S3、γ0、α为常数。 空气采用LS-DYNA软件提供的MAT_NULL材料模型和Linear_Polynomial状态方程[24]，即

p=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E，

(4)

式中：C0、C1、C2、C3、C4、C5、C6为无量纲常数。参数C0=C1=C2=C3=C6=0，其余参数取值如表1所示。

表1　水和空气的性能参数Tab.1　Performance parameters of water and air

2.2　网格划分与边界条件

1)网格划分。根据结构的对称性，为节省计算资源和时间，有限元模型采用1/4模型，射弹采用拉格朗日网格，水和空气的单元类型选用3D SOLID164，单元采用六面体单元，将计算域共划分为472 530个单元、497 028个节点，对计算水域和空气域局部网格进行加密，加密的区域内径为R10区域(见图2(b))，单个网格的长宽比在1～2之间，射弹下端距离水面20 mm(见图2(a))。

2)边界条件。采用1/4模型，在计算水域和空气域两个对称面上应分别满足对称边界x=0，z=0；在最外圆柱面和水底设置无反射边界条件，来模拟无限大水域。

2.3　计算结果

分别计算入水后射弹速度v、深度h随时间t的变化以及入水空泡形态的对比(见图3～图5)，将计算结果与文献[12]的结果进行比较，二者保持一致，说明本文算法的正确性。从图3中可以看出：射弹在垂直入水初始阶段速度衰减非常快，3 ms后速度衰减幅度趋于平缓，这是因为入水初始阶段承受的加速度大，随着入水深度的增加，其加速度值会逐渐降低。从图4中可以看出：射弹入水深度在入水最初时因为速度大而增加较快，之后趋于平缓；随着入水深度的增加，本文计算结果和文献[12]计算结果之差开始增大，这主要是由计算软件的不同造成的。

3　低亚声速射弹垂直入水数值计算

3.1　模型参数

射弹分别采用双圆台加圆柱体结构(见图6)，总长L=144 mm，材料采用钨合金，射弹采用Johnson-Cook模型，状态方程采用Gruneisen状态方程[25]。数学模型参数采用厘米- 克- 微秒单位制，水和空气采用的性能参数同2.1节，具体参数如下：

密度ρ=17.25×103kg/m3，弹性模量314 GPa，剪切弹性模量122 GPa，μ=0.29；材料性能常数A=1 506 MPa，B=177 MPa，C=0.016，n=0.12，m=1；室温300 K，熔化温度1 723 K，S1=1.23，S2=S3=0，γ0=1.54；钨合金中的声速4 029 m/s.

3.2　网格划分与边界条件

如图7所示，弹体、空气和水域采用1/4模型，射弹采用拉格朗日网格，水和空气的单元类型选用3D SOLID164，所有单元采用六面体单元，弹体共划分为105个单元，对计算水域和空气域局部网格进行加密，加密区域内径为R10 mm区域(见图7(b))，单个网格的长宽比在1～2之间，空气域划分为192 000个单元，水域划分为960 000个单元。共计1 152 105个单元，11 984 236个节点。

由于采用1/4模型，在计算水域和空气域两个对称面上应分别满足对称边界x=0，z=0；在最外圆柱面和水底设置无反射边界条件，来模拟无限大水域。

3.3　数值计算结果

3.3.1闭合时间和空泡形态

射弹入水速度分别取为100 m/s、200 m/s、300 m/s、400 m/s和500 m/s，计算出空泡面闭合、深闭合时间以及对应的无量纲时间和佛鲁德数分别如表2所示。由表2可以看出，在射弹入水速度小于500 m/s时，空泡先出现面闭合再出现深闭合现象。

以佛鲁德数为横坐标、无量纲时间为纵坐标，可得到空泡面闭合和深闭合无量纲时间与佛鲁德数的关系曲线如图8所示。由图8可以看出：空泡面闭合的无量纲时间随着佛鲁德数变化的幅度不大；随着佛鲁德数的增加，空泡深闭合的无量纲时间先缓慢增加、后减小，但总体趋势是减小的，且衰减的幅度较大。

图9为射弹在不同入水速度下空泡闭合时的形状。从图9中可以看出：在空泡发生面闭合时，闭合点周围的液面升高；闭合时，液体在空泡上方形成向上和向下两个方向的射流；随着射弹入水速度的增加，空泡发生面闭合时射弹的入水深度也随之增加。

表2　无量纲闭合时间与佛鲁德数关系Tab.2　Relationship between dimensionless closure time and Froude number

图10为射弹不同入水速度下空泡深闭合时的形状。从图10中可以看出：在空泡发生深闭合时，闭合位置并不会清晰地发生在一个点上，而是在一段距离上，最后在一个点处彻底断开，空泡迅速向上下方向收缩并迅速溃灭；随着射弹入水速度的增加，空泡发生深闭合时射弹的入水深度也随之增加，且喷溅更高，水面抬高更明显。

3.3.2入水深度、射弹速度、加速度以及阻力系数

图11为射弹在不同入水速度下入水深度随时间的变化情况。由图11可以看出，入水速度越大，入水相同深度所需的时间越短。

图12为不同入水速度下射弹速度随时间的变化情况。由图12可以看出：入水速度越大，速度衰减越快；在入水后短时间内射弹速度随时间呈线性衰减，但速度衰减非常缓慢。这主要是因为射弹采用的钨合金密度非常大、惯性大，水对其动能造成的损失较小，可见入水深度随射弹速度的增加而增加。

图13为不同入水速度下射弹阻力系数随时间的变化情况。从图13中可以看出：高速射弹在空中段飞行时的阻力系数与入水段相比非常小，撞水后阻力系数迅速达到最大峰值，然后快速震荡衰减，振荡的频率和幅度与最小计算步长以及输出步长相关，当头部第1节圆台完全入水后，阻力系数稳定在1附近，与经验公式Cd=0.82(1+σ)的理论计算值吻合良好，其中Cd为阻力系数，σ为空化数；阻力系数峰值随入水速度的增大而增大，在入水速度为300 m/s时达到峰值，然后减小。

3.3.3射弹入水空泡发展过程

图14为射弹以500 m/s速度入水时的空泡发展过程。从图14中可以看出：射弹入水后只有头部沾湿，然后迅速排开水、形成空泡，水沿着射弹表面向上运动、形成喷溅，在射弹周围的水面可以看到明显的抬高现象；射弹完全浸入水中后，在弹后形成一个空腔与大气相通，随着射弹入水深度的增加，空泡最大直径逐渐增大，当喷溅的水在表面汇合时形成面闭合，使空泡和大气隔断；此时空泡直径达到最大值，面闭合时由于水有动能，在拍击作用下，在面闭合最顶点会形成向上和向下两股射流，向下的射流使空泡的上部变成一个M型形状。随着射弹入水深度的继续增加，空泡在中部开始逐渐收缩，将空泡分成上下两段，形成深闭合，深闭合位置并不在清晰的一个点上，而是在一段距离上。至此空泡经历了形成、面闭合、扩张、收缩和深闭合等阶段。

3.3.4射弹动力学响应

图15为射弹加速度a随时间t的变化情况。由图15可见，射弹在撞击水面的瞬间，加速度达到最大值，然后急剧衰减，震荡后收敛在某一值附近，入水速度不同，加速度的峰值和收敛值也不同，它们随入水速度的增大而增大，这是因为入水速度越大，受到水的阻力就越大。

图16为入水瞬间von Mises应力响云图。从图16(a)可以看出：射弹在入水瞬间，应力主要集中在头部，最大应力单元为16和24；头部以外应力较小，当t=0.230 ms时射弹头部没入水中，最大应力仍然分布在头部区域，应力波已经在弹体中自下而上传播，如图16(b)所示。单元16和24的应力响应随时间变化的曲线如图17所示。由图17可以看出，射弹在入水瞬间应力达到峰值，然后快速震荡衰减并逐渐趋于收敛。射弹入水时如果结构发生破坏，则发生在头部的可能性将非常大。

4　结论

本文采用欧拉- 拉格朗日耦合算法，研究了90°锥角头型圆柱体以500 m/s速度垂直入水时的流体与固体耦合动力学问题，通过计算结果与已有文献[12]结果的对比验证了本文数值计算方法的有效性。基于本文数值计算方法，建立了双圆台圆柱射弹垂直入水的有限元模型，得到了低亚声速射弹入水时的空泡形态发展历程，分析了射弹不同入水速度对空泡面闭合和深闭合时间的影响，计算得到了速度、加速度以及阻力系数随时间的衰减曲线，并获取了射弹结构的动力学应力和应变响应。结果表明：射弹的密度越大，速度衰减越缓慢，可见高密度的射弹其射程更远；射弹在撞击水面的瞬间，加速度达到最大值，然后急剧衰减，头部的应力非常大；射弹触水瞬间阻力系数迅速达到最大峰值，然后快速衰减，当头部第1节圆台完全入水后，阻力系数会收敛并保持在1左右。

参考文献(References)

[1]陈九锡，颜开. 用MAC方法计算平头物体垂直等速入水空泡[J].水动力学研究与进展，1985 (1)：1-7.

CHEN Jiu-xi，YAN Kai. The calculation of vertical constant-speed water entry cavity of flat-nosed body using the MAC-method[J].Advances in Hydrodynamics，1985 (1)：1-7.(in Chinese)

[2]叶取源. 锥头物体垂直入水空泡的发展和闭合[J].水动力学研究与进展，1989 (2)：4-8.

YE Qu-yuan. Evolution and closure of cavity after vertical water entry of cone-head bodies[J]. Advances in Hydrodynamics，1989 (2)：4-8. (in Chinese)

[3]龚凯.基于光滑质点水动力学(SPH)方法的自由表面流动数值模拟研究[D].上海：上海交通大学，2009.

GONG Kai. A numerical study of free surface flow based on smoothed particle hydrodynamics(SPH) [D]. Shanghai: Shanghai Jiao Tong University，2009. (in Chinese)

[4]魏卓慧，王树山，马峰. 刚性截锥形弹体入水冲击载荷[J]. 兵工学报，2010，31(1)：118-120.

对文、理科学生在9项技能的自我评价上进行独立样本T检验（见表2），结果显示，除“翻译”的P值=0.0 22＜0.05外，其他8项的P值均大于0.0 5，表明不同学科的学生对于绝大多数技能的自我评价没有显著性差异。而理科生在“翻译”评价上的均值显著地高于文科生，比起口语和写作这种主动的创造性的输出，理科生更喜欢用积累的词汇机械地翻译给予的文字段落，很好地说明了英语课堂上理科生更消极被动的一面。

WEI Zhuo-hui, WANG Shu-shan, MA Feng. Diving impact load of rigid truncated conical projectile[J]. Acta Armamentarii，2010，31(1)：118-120.(in Chinese)

[5]张珂，颜开，褚学森. 基于LBM方法的圆盘等速入水空泡的数值模拟[J].船舶力学，2010，14(10)：1129-1133.

ZHANG Ke, YAN Kai, CHU Xue-sen. Numerical simulation of constant speed water-entry cavity based on LBM[J]. Journal of Ship Mechanics，2010，14(10)：1129-1133. (in Chinese)

[6]胡平超，张宇文，袁绪龙. 航行器垂直入水空泡特性与流体动力研究[J].计算机仿真，2011，28(6)：5-8.

HU Ping-chao, ZHANG Yu-wen,YUAN Xu-long. Research on cavitation and hydrodynamic of vertical water-entry for supercavitating vehicles [J]. Computer Simulation，2011，28(6)：5-8. (in Chinese)

[7]王聪，何春涛，权晓波.空气压强对垂直入水空泡影响的数值研究[J].哈尔滨工业大学学报，2012，44(5)：14-19.

WANG Cong,HE Chun-tao,QUAN Xiao-bo. Numerical simulation of the influence of atmospheric pressure on water-cavity formed by cylinder with vertical water-entry[J]. Journal of Harbin Institute of Technology，2012，44(5)：14-19. (in Chinese)

[8]何春涛，王聪，闵景新，等. 回转体匀速垂直入水早期空泡数值模拟研究[J].工程力学，2012，29(4)： 237-243.

HE Chun-tao,WANG Cong,MIN Jing-xin,et al. Numerical simulation of early air-cavity of cylinder cone with vertical water-entry[J].Engineering Mechanics，2012，29(4)： 237-243. (in Chinese)

[9]杨衡，孙龙泉，龚小超，等.弹性结构入水砰击载荷特性三维数值模拟研究[J].振动与冲击，2014，33(19)：28-34.

YANG Heng，SUN Long-quan，GONG Xiao-chao，et al. 3D numerical simulation of slamming load character for water entry of an elastic structure[J]. Journal of Vibration and Shock，2014，33(19)：28-34. (in Chinese)

[10]杨衡，张阿漫，龚小超，等.不同头型弹体低速入水空泡试验研究[J].哈尔滨工程大学学报，2014，35(9)：1060-1066.

YANG Heng，ZHANG A-man，GONG Xiao-chao，et al. Experimental study of the cavity of low speed water entry of different head shape projectiles [J]. Journal of Harbin Engineering University，2014，35(9)：1060-1066. (in Chinese)

[11]孙钊，曹伟，王聪，等. 表面润湿性对球体入水空泡形态的影响研究[J].兵工学报，2016，37(4)：670-676．

SUN Zhao,CAO Wei,WANG Cong,et al．Effect of surface wettability on cavitation of sphere during its water entry[J]. Acta Armamentarii，2016，37(4)：670-676．(in Chinese)

[12]马庆鹏，魏英杰，王聪，等.锥头圆柱体高速入水空泡深闭合数值模拟研究[J].兵工学报，2014，35(9)：1451-1457.

MA Qing-peng，WEI Ying-jie，WANG Cong,et al. Numerical simulation of deep closure of high-speed water entry cavity of cone-cylinder[J]. Acta Armamentarii，2014，35(9)：1451-1457. (in Chinese)

[13]顾建农，张志宏，范武杰．旋转弹丸入水侵彻规律[J].爆炸与冲击，2005，25(4)：341-349．

GU Jian-nong，ZHANG Zhi-hong,FAN Wu-jie．Experimental study on the penetration law for a rotating pellet entering water[J]. Explosion and Shock Waves，2005，25(4)：341-349．(in Chinese)

[14]顾建农，张志宏，王冲，等．旋转弹头水平入水空泡及弹道的实验研究[J].兵工学报，2012，33(5)：540-544．

GU Jian-nong,ZHANG Zhi-hong,WANG Chong,et al．Experimental research for cavity and ballistics of a rotating bullet entraining water levelly[J]. Acta Armamentarii，2012，33(5)：540-544．(in Chinese)

[15]Shiffman M，Spencer D C. The force of impact on a cone striking a water surface(vertical entry)[J]. Communications on Pure and Applied Mathematics，1951，4(4):379-417.

[16]Miloh T. Wave slam on a sphere penetrating a free surface[J]. Journal of Engineering Mathematics，1981，15(3): 221-240.

[17]Greenhow M. Wedge entry into initially calm water[J]. Applied Ocean Research，1987，9(4): 214-223.

[18]Korobkin A A. Asymptotic theory of liquid-solid impact[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,1997，355(1724): 507-522.

[19]Scolan Y M，Korobkin A A. Three-dimensional theory of water impact. Part 1. Inverse Wagner problem[J]. Journal of Fluid Mechanics，2001，440(41): 293-326.

[20]Korobkin A A，Wu G X. Impact on a floating circular cylinder[J]. Proceedings of the Royal Society A:Mathematical, Physical and Engineering Sciences，2000，456(2002): 2489-2514.

[21]Korobkin A A，Scolan Y M. Three-dimensional theory of water impact. Part 2. Linearized Wagner problem[J]. Journal of Fluid Mechanics，2006，549: 343-373.

[22]Xu G D，Duan W Y，Wu G X. Numerical simulation of oblique water entry of an asymmetrical wedge[J]. Ocean Engineering，2008，35(16): 1597-1603.

[23]张劲生，张嘉钟，王聪，等．超空泡射弹结构响应的流固耦合仿真研究[J].船舶力学，2011,15(7)：763-768.

ZHANG Jin-sheng，ZHANG Jia-zhong,WANG Cong,et al. FSI simulation on the structural response of a supercavitating projectile[J]. Journal of Ship Mechanics，2011,15(7)：763-768. (in Chinese)

[24]Varas D， Zaera R，López-Puente J，et al. Numerical modeling of the hydrodynamic ram phenomenon[J]. International Journal of Impact Engineering，2009，36(3)：363-374.

[25]Feli S，Asgari M R. Finite element simulation of ceramic/composite armor under ballistic impact[J].Composites:Part B，2011，42(4)：771-780.