HIFiRE-1飞行器激波与边界层干扰气动热研究

毛宏霞， 贾居红， 傅德彬， 姜毅

(1.北京理工大学 宇航学院， 北京 100081； 2.北京环境特性研究所 光学辐射重点实验室, 北京 100854)

0　引言

临近空间高超声速飞行器横跨连续流区、滑移流区、过渡流区和自由分子流区，受黏性效应、高温真实气体效应等多种因素影响，存在层流与湍流转捩、激波与边界层干扰等复杂现象，需要对高超声速飞行器气动力、热问题进行深入研究[1-2]。

裙体结构是高超声速飞行器后部结构的重要形式之一。在高超声速飞行时，气流经过裙体拐角受到压缩产生的激波和边界层相互干扰，不仅改变流场状态，也对裙体结构气动加热产生显著影响。激波与边界层干扰由于涉及激波和边界层两个原本就非常复杂的问题，因此在相应的机理研究或工程应用中，通常采用试验或数值方法，结合雷诺数、马赫数等流动条件对激波与边界层流动结构形态和气动加热特性等进行研究[3-5]。高超声速国际飞行研究试验(HIFiRE)是近年来澳大利亚国防科技集团(DSTO)、美国空军研究所(AFRL)联合昆士兰大学和波音公司开展的系列高超声速飞行试验项目，主要采用探空火箭发射进行飞行器的上升和再入试验，旨在通过低成本系列飞行试验进一步探索高超声速飞行器基础问题和物理现象，为下一代空天飞行器奠定技术基础[6]。第1项HIFIRE-1试验主要研究边界层转捩和激波与边界层干扰下的高超声速气动热问题，2010年3月进行了飞行试验，并获得上升和再入段压强、温度和传热数据[7]。飞行试验之外，MacLean等[8]和Wadhams等[9]先期进行了风洞试验，并研究了气动热力学及边界层激流片尺度的影响，结果表明裙体附近的流动分离与再附状态会引起再附区气动热的显著增加。Kimmel等[10]公布了HIFiRE-1飞行测试得到的基础气动数据。近年来，围绕HIFiRE-1试验模型对应的钝头体边界层转捩、柱裙模型激波与边界层干扰等复杂流动问题，一些科研人员利用风洞试验和数值计算开展了更为深入的研究。如Stanfield等[11]对边界层转捩进行风洞试验，明确了不同雷诺数下的头锥边界层转捩的位置和状态，Yentsch等[12]采用不同湍流模型模拟了气动力和气动热，表明k-ω模型模拟分离区过大，热流率偏低。这些研究为认识带裙体结构的激波与边界层干扰气动热问题提供了良好基础，但对于来流参数对激波与边界层干扰作用下换热能力、结构参数对流动状态以及气动加热的影响等，还有待进一步地分析和研究。

为更深入地研究高超声速来流条件下带裙体结构表面的激波与边界层干扰现象以及由此引起的气动热效应，本文采用数值计算方法，在相关文献结合来流条件对HIFiRE-1试验模型表面热流密度大小进行研究的基础上，重点从流动形态、斯坦顿数等角度出发，对激波与边界层干扰条件下的热流状态和换热能力进行研究；与此同时，同样结合流动状态，研究飞行器裙体张角、裙体长度等结构参数对气动加热的影响，并分析其机理。

1　理论模型与计算方法

1.1　理论模型

本文采用三维可压缩Navier-Stokes方程作为气体流动的基本方程，其基本形式可表示为

(1)

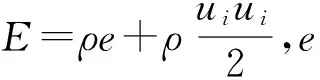
采用雷诺平均(RANS)方法对(1)式进行求解计算，并采用基于涡黏性假设的SST湍流模型和Realizablek-ε湍流模型[12-13]对模型方程进行封闭处理。其中，Realizablek-ε模型主要求解湍动能及其耗散项，并在耗散项中添加源项以改善逆压梯度流动模拟能力，SST模型在近壁面保留k-ω模型以捕捉到黏性底层的流动，在远离壁面的区域使用k-ε模型以弥补k-ω模型对入口湍流参数过于敏感的问题，具体表达式及参数见文献[13]。

封闭方程组采用有限体积法进行离散，黏性通量项用中心差分格式进行离散，无黏通量采用HLLC格式[14]进行离散，时间推进采用隐式方法。

1.2　计算模型

HIFiRE-1试验模型主要有鼻锥、锥体、柱体、裙体、延长体等部分，本文计算模型为简化后的锥- 柱- 裙结合体，具体尺寸见图1，其中球头半径为2.5 mm，锥体半锥角为7°，裙体张角为33°，裙体长度L为103.7 mm，其余尺寸如图1所示。模型验证采用文献[15]中的风洞试验数据，该试验来流条件为：压强4.62 kPa，温度231.7 K，速度2 182.4 m/s，马赫数7.16.

考虑到模型的对称性，本文仅对上半部分模型进行计算，几何模型以鼻锥前顶点为坐标原点。采用商用软件ICEM-CFD划分三维结构化网格，轴向、法向和周向节点数为311×101×108，在边界层内布置60层网格，网格总数330万，全局和局部网格形式如图2所示。采用商用计算流体力学软件CFD++，并使用MPICH2软件分块进行并行处理。计算模型的入口采用全参数超声速来流入口，下游出口采用超声速出口，壁面采用等温无滑移壁面条件，壁面温度300 K.

1.3　网格无关性验证

高超声速来流通过弓形激波后被强烈压缩，加之黏性滞止作用，来流速度在壁面处降为0. 根据能量守恒可知，外界来流巨大的动能转化为热能，必将在驻点区产生高温，这个高温区域在冷壁面必然产生很大的温度梯度。气动热数值模拟对网格异常敏感，壁面网格尺度稍有改变，热流密度误差就可能成倍增大[16]，因此必须严格限制壁面法向网格尺度。文献[17-18]研究表明，当壁面网格雷诺数接近1时，计算较为准确。

依据以上相关研究提出的壁面网格条件，初步设定第1层网格高度为5×10-7m. 为了验证网格准确性，结合风洞试验数据，采用3套网格方案进行试算，壁面法向网格高度Δn从5.7×10-7m依次递减至5.7×10-8m，网格延伸率保持在1.05，壁面y+从1.954减小到0.226，如表1所示，表中p为压强，Q为热流密度，Re为壁面网格雷诺数。

表1　网格无关性验证Tab.1　Grid independence

模拟得到的激波与边界层干扰流区壁面压强和热流分布如图3所示。本文试验数据均来源于Wadhams等[9]的风洞试验。从图3中可以看出，对于网格方案2和网格方案3，分离区内法向和轴向网格都足够密集，壁面最大y+小于0.5，计算分析获得的驻点及壁面的热流和压强吻合良好，并与试验数据误差较小，可以认为网格已满足法向无关性要求。需要补充说明的是，轴向网格对锥面/圆柱过度区域及拐角区域的流动和热流状态同样具有较大影响，研究表明对于本文所采用的模型结构，当拐角或过渡区域轴向网格尺寸小于0.3 mm、网格缩放比例为1.05、周向网格布置间隔为2.4°时，能够保证轴向和周向的网格无关性条件。

1.4　湍流模型校验

除网格因素之外，气动热模拟还必须考虑湍流模型的影响。MacLean等[8]计算表明SA模型预测分离区过小；Yentsch等[12]对HIFiRE-1试验模型上升段气动热的模拟表明k-ω模型模拟分离区过大，热流率偏低。因此，本文对这两类湍流模型不再进行分析，重点对应用较为广泛的两方程k-ε模型和SST模型进行对比验证。

图4给出了两种湍流模型对应的壁面热流和压强分布。从图4中可以看出，两种湍流模型的模拟分离泡大小相当、位置基本相同，k-ε模型模拟平台区压强稍大，再附区壁面压强稍低于SST模型，误差在3%以内。但从图4(a)可以明显看出二者模拟得到的壁面热流差别，SST模型高估了再附点热流，峰值误差9.8%，而k-ε模型完全低估了分离区热流密度，最大误差-27.9%. 由此可以看出，湍流模型对激波与边界层干扰气动热模拟准确性也有较大影响。考虑到SST模型对再附点热流峰值预估误差小于10%，本文后续使用SST模型进行计算和分析。

2　结果与分析

2.1　激波与边界层干扰气动热

结合前述风洞试验对应的计算工况，从模拟得到的壁面热流和压强分布(见图3和图4)可以看出，受柱裙拐角气流压缩影响，气流边界层在1.55 m处开始分离，此时壁面热流和压强上升并保持一段平台期，而后在1.63 m处开始突增，并于1.66 m处再附于裙体斜面，此时热流密度和压强均迅速增加并出现峰值，二者最大值分别为388.4 W/cm2和135.4 kPa. 而后在扇形压缩波区域，热流密度和压强快速降低并趋于常数，气流流过延长体部分时迅速膨胀，热流密度和压强都迅速降低。对比文献[9]试验数据可以看出，计算获得的分离位置、再附位置均与试验状态吻合良好。图5(a)为数值模拟获得的马赫数Ma分布云图，显示了拐角处流场特性和激波结构。由图5(a)可知，来流由左向右，上游流动分离诱导出一个明显的分离激波，向上偏折后再附到裙体壁面，形成再附激波。拐角处分离激波带来的大逆压梯度使壁面边界层发生较为严重的变形，并向上游和下游传播，造成拐角附近边界层膨胀，形成气泡状分离区，并且分离区内为亚声速流动。再附激波沿裙体向下游发展并远离壁面，形成扇形压缩波，扇形波流经裙体延长部分时气流迅速膨胀，出现明显的膨胀波。图5(b)给出了流场压强分布，图5(c)给出了流场温度和壁面热流分布。由图5(b)和图5(c)可知，在分离区内为高温区，边界层再附后出现环形高热流带。此外，在裙体前沿的局部区域，受边界层分离引起的流动振荡现象影响，压强和热流呈现周向非均匀分布。本文采用时间推进法进行迭代求解，能够在一定程度上捕获这类局部流动振荡现象。

2.2　来流条件对壁面热流的影响分析

为了研究来流条件对激波与边界层干扰气动热的影响，选择不同来流雷诺数、马赫数的工况进行计算分析。计算模型的基本状态如表2所示。

表2　来流参数与裙体尺寸Tab.2　Free stream parameters and structure size

2.2.1来流雷诺数影响

首先考虑来流马赫数、温度等条件保持不变的前提下，雷诺数从1.738×107降低到3.280×106和1.640×106，计算获得的分离区热流及压强分布状态。

图6(a)给出了不同雷诺数下的壁面热流分布。从图6中可以看出，模拟得到的流场结构、分离区位置基本保持不变，分离点仍保持在1.55 m位置附近，但壁面压强和热流发生了较大变化。当雷诺数降低到3.28×106时，壁面热流得到显著降低，再附点热流峰值由394.4 W/cm2降低到185.1 W/cm2；当雷诺数降低到1.64×106时，壁面热流继续变化，再附点热流峰值降低到108.9 W/cm2. 事实上，随着雷诺数的降低，来流密度降低，热流密度自然也会降低，表明计算结果与理论预计是相符的。图6(b)给出了压强分布情况，从中可以看出，壁面压强同样持续变化，峰值由132.7 kPa分别降低到48.3 kPa和24.8 kPa，平台区压强由10 kPa降低到4 kPa和2 kPa.

2.2.2来流马赫数影响

在其余参数不变情况下，马赫数由7.16降低至5.00和3.00，壁面热流和压强结果如图7(a)和图7(b)所示。从图7(a)和图7(b)中可以看出：马赫数降低后，壁面热流密度大幅度降低；马赫数为5.00时热流峰值为101.2 W/cm2；马赫数为3.00时壁面热流基本保持平缓发展，峰值热流密度仅为12.8 W/cm2；壁面压强也大幅度降低，峰值分别为69.7 kPa和25.8 kPa.

此时，流场结构如图7(c)和图7(d)所示。从图7(c)和图7(d)可以看到：马赫数降低后激波厚度增大，分离泡范围增加；流场波系结构较为清晰，分离激波向下游发展，与再附激波相交，形成三叉激波，这也是再附点压强和热流急剧上升的主要原因；马赫数为3.00时三叉激波距离裙体壁面的位置明显远于马赫数为5.00时的结果，这说明来流马赫数对再附点热流大小有重要影响。

2.2.3来流条件影响壁面热流的综合分析

为进一步明确来流条件对壁面热流的影响，下面分析不同来流条件下表征换热能力的斯坦顿数St变化情况。St采用来流密度、速度和温度作为参考值。

图8给出了不同雷诺数和不同马赫数条件对应的St数分布情况。从图8(a)可以看出：在不同来流条件下，受裙体上气流再附效应影响，裙体再附区域的St数均显著增加，表明换热能力在这一区域明显增强；对于不同来流条件，随着雷诺数的增加，气流再附效应引起的St数增量幅值减小，表明来流雷诺数增加虽然使裙体上最大热流密度绝对值增加，但表征换热能力的St数反而降低。从图8(b)可以看出，随着来流马赫数(对应来流速度)的增加，裙体上St数显著增加，表明气流再附引起的换热能力增加。结合具体研究工况，可明确：随着来流密度的增加，表征换热能力的St数减小；随着来流速度的增加，表征换热能力的St数增加。

2.3　裙体结构对壁面热流的影响分析

2.3.1裙体张角影响

结合表2所示来流条件，选择裙体张角从33°变化为27°、30°、37°进行计算，获得壁面热流分布与压强分布如图9(a)和图9(b)所示，马赫数分布如图9(c)和图9(d)所示。由图9可以看出：当张角缩小至30°时，边界层分离区变小，上游分离点和下游再附点都有回缩趋势，分离点位于1.58 m，再附点位于1.66 m，壁面热流和压强相应降低，峰值分别降到318 W/cm2和104.1 kPa；当裙体张角进一步缩小至27°时，分离泡缩小至即将消失，来流在拐角处基本直接沿壁面向上流动，受外侧来流影响，同样形成扇形压缩波；当增大张角至37°时，激波与边界层干扰分离区增大，分离点向上游发展至1.52 m，再附点向下游发展至1.67 m，裙体表面热流密度和压强相应上升，再附点热流和压强峰值升高到481.7 W/cm2和172 kPa.

2.3.2裙体长度影响

在流动参数保持不变情况下，通过控制改变裙体长度L，计算后得到的壁面热流和压强分布如图10(a)和图10(b)所示，马赫数分布如图10(c)和图10(d)所示。由图10可见，当裙体长度从103.7 mm缩短到82.0 mm时，流动依然完成在裙体壁面的再附，壁面热流密度和压强分布基本保持与原模型一致。为了探究流动无法完成再附情况下的壁面热流变化，进一步将裙体长度缩短至32.0 mm位置，此时流动依然被压缩产生边界层分离区，但剪切层无法在裙体斜面完成再附，表现为分离泡缩小，壁面热流和压强无法达到峰值即开始迅速降低。从图5中流场马赫数分布可以看出，分离激波的发展会受到自由来流的影响，为了验证以上判断，把裙体长度增大至202.0 mm，此时飞行器锥体外部来流与裙体上方分离激波相交，分离激波受压之后沿壁面向下游发展，直接导致扇形压缩波内压强增大，进而引发边界层分离泡增大，分离点前移，再附点后移。此时，模拟得到的壁面热流和壁面压强出现明显上升趋势，热流峰值464.1 W/cm2，压强峰值159.53 kPa.

3　结论

本文对HIFiRE-1高超声速飞行器激波与边界层干扰气动热问题及影响因素进行了研究，得到以下结论：

1)当来流雷诺数改变时，分离区流场结构变化较小，但热流密度随着雷诺数的增加而增加。当来流马赫数改变时，激波与边界层干扰区的激波结构发生相应改变，热流密度同样随着马赫数的增加而增加。此外，在来流变化过程中，裙体气流再附区域换热能力也会产生显著变化。随着来流速度增加，裙体上气流再附区表征换热能力的St数增加；而随着来流密度增加，再附区表征换热能力的St数减小。

2)当裙体张角改变时，分离区壁面热流分布大幅改变，当裙体张角增大到37°时，分离区增大，分离点向上游发展，再附点向下游发展；当裙体张角减小到27°时，分离区基本消失，壁面热流将近降到一半。裙体长度增大会导致分离泡增大、热流增加，裙体长度减小至分离流无法完成再附时，壁面热流无法达到峰值并迅速降低。

参考文献(References)

[1]Persovaa M G, Soloveichika Y G, Belovb V K. Modeling of aerodynamic heat flux and thermoelastic behavior of nose caps of hypersonic vehicles [J].Acta Astronautica, 2017, 136(1): 312-331.

[2]张志豪, 孙得川.飞行器气动加热烧蚀工程计算[J]. 兵工学报, 2015, 36(10): 1949-1954.

ZHANG Zhi-hao, SUN De-chuan. Calculation of aerodynamic heating and ablation of multi-layer thermal protection material[J]. Acta Armamentarii, 2015, 36(10): 1949-1954. (in Chinese)

[3]童福林, 李新亮, 唐志共, 等. 转捩对压缩拐角激波/边界层干扰分离泡的影响[J]. 航空学报， 2016, 37(10): 2909-2912.

TONG Fu-lin, LI Xin-liang, TANG Zhi-gong, et al. Transition effect on separation bubble of shock wave/boundary layer interaction in a compression ramp[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(10): 2909-2912. (in Chinese)

[4]宋友富, 徐晶磊, 张杨, 等. 压缩拐角激波/边界层干扰的可压缩湍流模型研究[J]. 推进技术, 2017, 38(2): 281-288.

SONG Yong-fu, XU Jing-lei, ZHANG Yang, et al. Research of compressible trubulence model in shock wave/boundary-layer interaction flow at a compression corner[J]. Journal of Propulsion Technology, 2017, 38(2): 281-288. (in Chinese)

[5]董祥瑞, 陈耀慧, 董刚, 等. 基于双微楔的高超声速激波与边界层干扰控制研究[J]. 兵工学报, 2016, 37(9): 1624-1632.

DONG Xiang-rui, CHEN Yao-hui, DONG Gang, et al. Research on control of hypersonic shock wave/boundary layer interactions by double micro-ramps[J]. Acta Armamentarii, 2016, 37(9): 1624-1632. (in Chinese)

[6]Bisek N J. High-fidelity simulations of the HIFiRE-6 flow path, AIAA-2016-1115[R]. Reston, VA, US: AIAA, 2016.

[7]Kimmel R L, Adamczak D W. HIFiRE-1 flight trajectory estimation and initial experimental results, AIAA-2011-2358 [R]. Reston, VA, US: AIAA, 2011.

[8]MacLean M, Wadhams T, Holden M, et al. Ground test studies of the HIFiRE-1 transition experiment—part 2: computational analysis[J]. Journal of Spacecraft and Rockets, 2008, 45(6): 1149-1164.

[9]Wadhams T, Mundy E, MacLean M, et al. Pre-flight ground testing of the full-scale HIFiRE-1vehicle at fully duplicated flight conditions: part II, AIAA-2008-0639[R]. Reston, VA, US: AIAA, 2008.

[10]Kimmel R L, Adamczak D W. HIFiRE-1 preliminary aerothermodynamics measurements, AIAA-2011-3413[R]. Reston, VA, US: AIAA, 2011.

[11]Stanfield S A, Kimmel R L, Adamczak D W, et al. Boundary layer transition experiment during reentry of HIFiRE-1[J]. Journal of Spacecraft and Rockets, 2015, 52(3): 637-649.

[12]Yentsch R J, Gaitonde D V, Kimmel R L. Performance of turbulence modeling in simulation of the HIFiRE-1 flight test[J]. Journal of Spacecraft and Rockets, 2014, 51(1): 117-127.

[13]Rautaheimo P R. Developments in turbulence modeling with Reynolds-averaged Navie Stokes equations[M]. Helsinki, Finland: Finnish Academies Technology Press, 2001: 17-19.

[14]Xu L, Wu Q J, Weng P F. HLLC Riemann solver based on high-order reconstruction for unsteady inviscid compressible flows[C]∥Proceedings of IEEE International Conference on Computer Science and Automation Engineering. Shanghai, China: IEEE, 2011: 618-622.

[15]Holden M, Wadhams T, MacLean M, et al. Experimental studies of shock wave/turbulent boundary layer interaction in high Reynolds number supersonic and hypersonic flows to evaluate the performance of CFD codes, AIAA-2010-4468[R]. Reston, VA, US: AIAA, 2010.

[16]Yang J L, Liu M. A wall grid scale criterion for hypersonic aerodynamic heating calculation[J]. Acta Astronautica, 2017, 136(1): 137-143.

[17]张智超, 高振勋, 蒋崇文, 等. 高超声速气动热数值计算壁面网格准则[J]. 北京航空航天大学学报, 2015, 41(4): 594-600.

ZHANG Zhi-chao, GAO Zhen-xun, JIANG Chong-wen, et al. Grid generation criterions in hypersonic aeroheating computations[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(4): 594-600. (in Chinese)

[18]Sohag F A, Mohanta L, Cheung F B. CFD analyses of mixed and forced convection in a heated vertical rod bundle[J]. Applied Thermal Engineering, 2017, 117(4): 85-93.