低速巡飞器倾斜转弯鲁棒反演控制律设计

王娜， 孙瑞胜， 杨智刚， 傅健

(南京理工大学 能源与动力工程学院， 江苏 南京 210094)

0　引言

巡飞器成本低、尺寸小、隐蔽性好[1]，能够长时间在空中巡飞侦察、发现敏感目标并对其实施精确打击[2]，是现代战场不可或缺的新概念武器。对于面对称的巡飞器，多采用倾斜转弯(BTT)控制方式，以充分利用巡飞器的机动能力[3]。然而，巡飞器BTT控制时，需要其绕速度矢量迅速滚转，使得巡飞器的俯仰、偏航通道存在耦合，因此传统的三通道单独设计控制律不再适用[4-5]。

目前，对于BTT控制解耦设计的方法有多种，主要分为3类：一是采用经典控制理论，通过增加一个交耦支路来抵消耦合项对偏航回路和俯仰回路的影响，从而能够独立设计各通道[6]；二是将耦合项看作干扰，利用现代控制理论补偿，如童春霞等[7]采用变结构滑模方法设计了输出解耦控制律；三是采用多变量频域理论，将耦合的多通道转化为单通道问题，如郭鸿武等[8]采用奈奎斯特阵列法设计了动态预补偿器。

除了耦合问题外，低速巡飞器在受到较大的外部干扰时，其动力学模型存在匹配不确定项与非匹配不确定项[9]。因此，寻找合适的控制方法是巡飞器控制系统设计的关键。反演控制技术是近几年发展起来的一种非线性反馈控制设计方法，它基于Lyapunov函数的逐步递归方法，将一定的系统状态作为虚拟控制来满足全局控制目标，其稳定性、收敛性和鲁棒性都已得到证明[10-12]。但当控制系统的不确定项较大时，反演法自身的鲁棒性能将不再满足要求。为此，国内外学者大多采用自适应反演法补偿不确定项，以增强系统的鲁棒性。但该方法要求对不确定项进行参数化，且存在计算膨胀问题[13-15]。为了解决这个问题，学者们将反演控制、自适应控制与滑模控制结合起来[16-17]，取得了良好的控制效果。

本文在反演控制的基础上设计了一种鲁棒反演控制器。针对巡飞器动力学模型存在不确定项的问题，根据Leibniz法则建立不确定项的模型，并将不确定项分为匹配与非匹配项，分别设计鲁棒函数。利用改进的符号函数抵消非匹配不确定项的影响；采用Lyapunov理论重新设计技术补偿匹配不确定项。该方法直接对多输入多输出控制系统进行设计，不仅能够解决BTT控制耦合问题，而且不存在计算膨胀的问题，在不确定干扰条件下能够快速准确跟踪指令。

1　动力学建模

以巡飞器的攻角α、侧滑角β和滚转角γ以及角速度ωx、ωz和ωy作为三通道数学模型的状态量，以舵偏角δx、δz和δy作为控制量，建立巡飞器的动力学模型[18]如下：

(1)

式中：Jx、Jz和Jy分别为巡飞器相对于弹体坐标系各轴的转动惯量；a1～a5、b1～b5和c1、c3分别为俯仰、偏航、滚转通道的动力学系数。

1.1　BTT控制建模

(1)式可写成如下块控形式：

(2)

式中：t为时间；状态变量x=[γαβ]T、ω=[ωxωzωy]T；控制变量u=[δxδzδy]T;系统矩阵与控制矩阵为

(3)

(4)

(5)

(6)

(7)

由于BTT控制时ωx值较大，不能将ωxβ、ωxα、ωxωy和ωxωz等耦合项忽略或者当作扰动处理，三通道独立设计控制系统不再适用。因此，本文采用反演算法直接对该多输入多输出的系统进行控制，设计控制变量u，使得x跟踪其指令xc=[γcαcβc]T。

1.2　不确定项建模

低速巡飞器由于飞行速度较低，容易受到风等外部因素干扰，主要表现为速度的不确定性。除此之外，由于气动计算条件的限制及飞行速度的不确定性，巡飞器动力学模型中的气动系数与实际飞行时的气动系数之间存在较大偏差。因此，其不确定项主要由气动系数与速度的不确定引起。

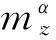
(8)

式中：密度ρ、特征面积S、特征长度L以及Jz为确定值；a2n为a2的确定项；σa2为a2的偏量函数。由(8)式可以看出，利用Leibniz法则建立的不确定项模型能够更直观地反映气动系数和速度变化对动力学系数产生的影响，比较准确地推导出动力学系数的变化范围。按照(8)式的方法可以推导出所有的动力学系数不确定项表达式，不再赘述。

对所有动力学系数不确定项建模后，则(2)式可以写成确定项与不确定项之和的如下形式：

(9)

式中：umax为u的上界，补偿了u对x的影响；fxn、fωn和gωn分别为fx、fω和gω的确定项；Δfxu、Δfω和Δgω为不确定项，其表达式如下：

(10)

(11)

(12)

从(12)式容易看出，存在连续函数Δg′ω，且‖Δg′ω‖<1，使得Δgω=gω(x,t)Δg′ω，因此Δgω为匹配不确定项，其余为非匹配不确定项[9]。

忽略(9)式中的不确定项，巡飞器控制系统的标称模型可写成如下形式：

(13)

下文中为了表达简洁，将确定项fn统一简写为f.

1.3　鲁棒控制边界函数

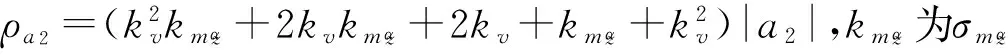
(14)

(15)

(16)

2　控制器设计

本文设计鲁棒反演控制的基本思路是：首先采用传统反演法设计标称模型的控制律，即名义控制律；然后分别利用鲁棒函数补偿非匹配与匹配不确定项的影响，从而获得完整的鲁棒控制函数。

2.1　名义控制律

反演控制是一种非线性系统设计方法，它通过引入虚拟控制，将复杂的非线性系统分解成多个更简单和阶数更低的系统，然后选择适当的Lyapunov函数来保证系统的稳定性，并逐步导出最终的控制律及参数自适应律，实现对系统的有效控制和全局调节，具有系统化、结构化特点[10]。巡飞器名义控制律具体设计过程如下：

步骤1用ωc表示角速度的虚拟控制指令，通过设计ωc使得x的误差ex=x-xc趋近于0. 此时ex的导数为

(17)

步骤2通过控制u，使得ω的误差eω=ω-ωc趋近于0，使步骤1的假设条件成立。

系统误差为

(18)

定义增广Lyapunov函数为

(19)

(20)

(21)

2.2　非匹配项控制

记un为名义控制，则鲁棒控制律u=un+uu+um，其中，uu为非匹配项的控制律，um为匹配项的控制律。为了抵消非匹配不确定项对系统的影响，设计(22)式所示的关于变量s的鲁棒函数ν，其幅值为非匹配项的边界函数ρu.ν通过在符号函数的基础上增加斜率为σs的衰减项，可获得比符号函数更准确的控制效果，且能够避免直接由符号函数sign(s)逼近不确定项所引起的系统振颤，从而有鲁棒控制函数为

ν=ρusign(s)(1-e-σs|s|)=ρusigm(s)，

(22)

其1阶导数为

(23)

由1.3节可知，存在非匹配项的控制系统为

(24)

系统误差为

(25)

(26)

采用鲁棒函数ρfxusigm(ex)来抵消不确定项Δfxu的影响，则虚拟控制ωc可写成如下形式：

(27)

此时系统的误差为

(28)

从而包含非匹配项的控制变量u′可以写成如下形式：

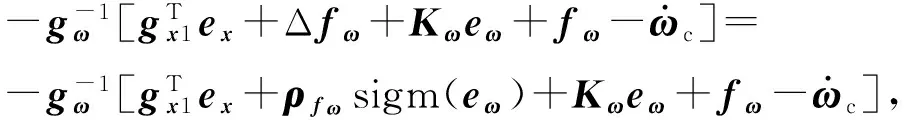
(29)

式中：

(30)

用ρfxu代替不确定项Δfxu，则

(31)

故

(32)

(33)

又因为

(34)

(35)

所以

(36)

式中：ex的残差项res(|ex|)=|ex|T(ρfxue-σex|ex|)，eω的残差项res(|eω|)=|eω|T(ρfωe-σeω|eω|)有界且有最大值。事实上，

(37)

(38)

(39)

2.3　匹配项控制

下面采用Lyapunov再设计技术[19]补偿匹配不确定项。由1.2节可推导出只包含匹配不确定项的模型为

Δg′ω(x,t))u，

(40)

式中：I3为3阶单位矩阵。该系统的Lyapunov再设计函数的导数为

(41)

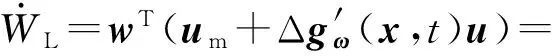
(42)

(-η(1-k0)+ρL)‖wT‖.

(43)

当w=0时，控制律um不连续，可能会造成系统振颤。为了使控制律导数连续，可以再次使用sigm函数来解决，从而可得巡飞器总的鲁棒控制律为

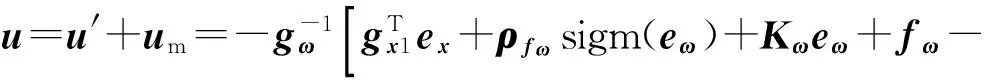
(44)

3　数值仿真

为了验证所提出的鲁棒反演控制方法的正确性和有效性，下面以某BTT近程低速巡飞器为例设计鲁棒反演控制律，并与名义控制律进行对比研究。

3.1　标称模型条件下的数值仿真

图1给出了标称模型条件下鲁棒反演控制系统和名义控制系统的跟踪误差er、eα、eβ对比曲线，图2给出了标称模型条件下鲁棒反演控制系统和名义控制系统的舵角偏角σx、σz、σy对比曲线。由图1可以看出，两种方法的γ、α、β的误差均逐渐减小，1 s后接近0°，从而验证了鲁棒反演算法的正确性。由图2可以看出，舵偏曲线的瞬态过程虽稍有不同，但最后稳态值几乎相等。

3.2　存在不确定项的数值仿真

1)从图3可以看出，鲁棒反演控制系统在存在干扰的情况下也能够准确跟踪指令信号，调节时间为1 s.

2)从图4～图6可以看出，名义控制系统跟踪指令滚转角与侧滑角时不存在静差，但跟踪指令攻角时存在1.4°的静差，不满足要求。

3)从图7、图8可以看出，鲁棒反演控制系统角速度变化范围在-10°/s～80°/s之间，舵偏角变化范围在-6°～1°之间，变化速率最大值为80°/s左右，无剧烈振颤，便于舵机执行。

4　结论

本文提出了一种利用微积分学中Leibniz法则建立不确定项的方法，该方法能够更直观地反映气动系数及速度变化对动力学系数的影响。针对块控模型中存在非匹配和匹配不确定项的问题，基于sigm函数分别设计了鲁棒函数进行补偿。仿真结果表明，当系统存在较大不确定项时，鲁棒反演控制相对于传统的反演法能够有效消除系统误差，并准确快速跟踪控制指令，具有强鲁棒性。

参考文献(References)

[1]王志飞, 王华, 赵春明,等. 巡飞器巡飞段动力学建模与仿真研究[J]. 系统仿真学报, 2010, 22(增刊1):196-198.

WANG Zhi-fei, WANG Hua, ZHAO Chun-ming, et al. Flight dynamics modeling and simulation of loitering monition in loitering phase [J]. Journal of System Simulation, 2010, 22(S1): 196-198. (in Chinese)

[2]李长文, 胡永琴, 张建生. 陆基远程巡飞武器装备发展研究[J]. 飞航导弹, 2013,42(11):20-24.

LI Chang-wen, HU Yong-qin, ZHANG Jian-sheng. Research on development of ground-based long-range loitering weapon equipment [J]. Winged Missiles Journal, 2013, 42(11):20-24. (in Chinese)

[3]Xin M, Balakrishnan S N, Stansbery D, et al. Nonlinear bank-to-turn/skid-to-turn missile outer-loop/inner-loop autopilot design with theta-D technique[C]∥Proceedings of AIAA Guidance, Navigation, and Control Conference and Exhibit. Hilton Head, SC, US: AIAA, 2013.

[4]曾宪法, 王小虎, 张晶. 基于增量模型的BTT导弹新型解耦补偿控制[J]. 北京航空航天大学学报, 2012, 38(12):1611-1615.

ZENG Xian-fa, WANG Xiao-hu, ZHANG Jing. Novel decoupling-compensating control based on incremental model for bank-to-turn missiles [J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(12):1611-1615. (in Chinese)

[5]张颖昕, 董朝阳, 王青,等. 倾斜转弯导弹的分散自适应滑模解耦控制方案[J]. 兵工学报, 2010, 31(7):906-910.

ZHANG Ying-xin, DONG Chao-yang, WANG Qing, et al. Decentralized adaptive sliding mode decoupling control scheme for bank-to-turn missile [J]. Acta Armamentarii, 2010, 31(7):906-910. (in Chinese)

[6]赵霞. 防空导弹BTT控制解耦算法[J]. 兵器装备工程学报, 2013, 34(8):37-39.

ZHAO Xia. Research on BTT control decoupling algorithm for the air-defense missile [J]. Journal of Ordnance Equipment Engineering, 2013, 34(8):37-39. (in Chinese)

[7]童春霞, 王正杰, 张天桥. BTT导弹的变结构解耦控制系统设计[J]. 宇航学报, 2006, 27(1):27-30.

TONG Chun-xia, WANG Zheng-jie, ZHANG Tian-qiao. Decoupling design for BTT missile using variable structure approach[J]. Journal of Astronautics, 2006, 27(1):27-30. (in Chinese)

[8]郭鸿武, 刘明俊. BTT导弹自动驾驶仪的多变量频域法解耦设计[J]. 国防科技大学学报, 1999, 25(6):13-16.

GUO Hong-wu, LIU Ming-jun. Decoupling design for bank-to-turn missile autopilot using multivariable frequency-domain approach [J]. Journal of National University of Defense Technology, 1999, 25(6):13-16. (in Chinese)

[9]Isidori A. Nonlinear control systems [M]. 2nd ed. New York，NY,US: Springer, 1989.

[10]Oort E V, Sonneveldt L, Chu Q P, et al. Modular adaptive input-to-state stable backstepping of a nonlinear missile model[C]∥Proceedings of AIAA Guidance, Navigation and Control Conference and Exhibit. Hilton Head, SC, US:AIAA，2013.

[11]Chen M, Ge S Z S, Ren B B. Adaptive tracking control of uncertain MIMO nonlinear systems with input constraints [J]. Automatica, 2011, 47(3):452-465.

[12]Gils P V, Kampen E J V, Visser C C D, et al. Adaptive incremental backstepping flight control for a high-performance aircraft with uncertainties[C]∥Proceedings of AIAA Guidance, Navigation, and Control Conference. San Diego, CA, US: AIAA, 2016.

[13]张强, 吴庆宪, 姜长生, 等. 基于Backstepping的近空间飞行器鲁棒自适应姿态控制[J]. 南京航空航天大学学报, 2013, 45(5):590-598.

ZHANG Qiang, WU Qing-xian, JIANG Chang-sheng, et al. Robust adaptive control for attitude system of near space vehicle via backstepping method [J]. Journal of Nanjing University of Aeronautics & Astronautics, 2013, 45(5): 590-598. (in Chinese)

[14]国海峰, 黄长强, 丁达理,等. 高超声速滑翔式BTT导弹鲁棒反演控制器设计[J]. 电光与控制, 2014, 21(3):66-71.

GUO Hai-feng, HUANG Chang-qiang, DING Da-li, et al. Robust backstepping controller design for the supersonic gliding BTT missile [J]. Electronics Optics & Control, 2014, 21(3):66-71. (in Chinese)

[15]陈强, 任雪梅, 那靖. 参数不确定混沌系统的自适应Backstepping控制[J]. 北京理工大学学报, 2011, 31(2):158-162.

CHEN Qiang, REN Xue-mei, NA Jing. Adaptive Backstepping control of chaotic system with uncertain parameters [J]. Transactions of Beijing Institute of Technology, 2011, 31(2):158-162. (in Chinese)

[16]高长生, 荆武兴, 李君龙. 基于自适应反演法的质量矩导弹控制律设计[J]. 兵工学报, 2011, 32(6):686-690.

GAO Chang-sheng, JING Wu-xing, LI Jun-long. Robust adaptive backstepping control for mass moment missile with dynamic surface filtering [J]. Acta Armamentarii, 2011, 32(6):686-690. (in Chinese)

[17]张金鹏, 周池军, 雷虎民. 基于滑模反演控制方法的纵向制导控制一体化设计[J]. 固体火箭技术, 2013, 36(1):11-16.

ZHANG Jin-peng, ZHOU Chi-jun, LEI Hu-min. Integrated guidance and control design based on sliding-mode and backstepping control [J]. Journal of Solid Rocket Technology, 2013, 36(1):11-16. (in Chinese)

[18]Duan Z S, Huang L, Yang J Y. On decoupled or coupled control of bank-to-turn missiles [J]. Science China: Information Sciences, 2015, 58(5):052204-1-052204-13.

[19]Hwang E J, Kang H S, Hyun C H, et al. Robust backstepping control based on a Lyapunov redesign for skid-steered wheeled mobile robots[J]. International Journal of Advanced Robotic Systems, 2013, 10(1):1-8.