细长体自旋与锥动耦合运动作用下的流动结构研究

彭程， 郭洋

(1.海鹰航空通用装备有限责任公司， 北京 100074； 2.北京空天技术研究所， 北京 100074)

0　引言

旋转飞行可以简化导弹的控制系统，用一个控制通道实现俯仰和偏航两个方向的控制,减小推力偏心、质量偏心、气动偏心等非对称因素对飞行性能的不利影响。然而，当飞行器绕其轴线旋转飞行时，旋转对边界层的剪切效应会引起体涡的非对称分离以及边界层转捩区的非对称，产生新的不对称气动力和气动力矩，其中最突出的就是面外力和面外力矩。旋转导弹在大机动情况下，非定常流动分离加强，漩涡在演化过程中的拉伸扭转会出现配对、合并与破裂现象，形成多尺度涡结构。不同尺度的漩涡相互作用会改变弹体和尾翼表面的压力分布，进而产生非线性面外力和面外力矩，导致锥形运动的产生。

对于细长体旋转弹而言，在弹体自旋飞行过程中，由于旋转诱导的面外力和面外力矩与弹体长径比的平方呈正比，使其更容易产生锥形运动。锥形运动不稳定现象会导致弹体运动的锥动角增大，进而影响导弹射程和命中精度，严重时甚至会导致导弹发射失败。

20世纪60年代，美国Nite-hawk探空火箭在50余次飞行试验中有近20次出现了发散的锥形运动[1]。西班牙140 mm火箭弹在28次飞行试验中出现了9次锥形运动[2]。美国、英国、澳大利亚联合进行的无控炸弹飞行动力学研究，着重研究了导弹下落过程中产生锥形运动的原因及其抑制措施[3]。我国在无控导弹的飞行试验中也有类似锥形运动的现象发生，使得其射程大大降低。

美国国家航空航天局(NASA)从20世纪80年代开始研究旋转弹体的气动特性，进行了一系列风洞试验，近年又开展了更高精度的瞬态测力试验[4-6]。Nygaard等利用重叠网格技术，开展了旋转状态下旋转弹标准试验模型(FM-3)标模的气动特性研究，分析了不同网格规模对模型气动系数以及分离涡形态的影响[7]。伴随着计算流体力学(CFD)软硬件能力的提高，21世纪初，NASA计算了大量旋转导弹的动态流场和气动特性[8-12]。2010年， Sheng等[13]利用高精度非结构网格实现了自旋运动和鸭舵俯仰振荡的耦合求解，并对不同精度下鸭舵分离涡与边界层的干扰形态进行了分析。20世纪80年代开始，苗瑞生等[14]对旋转弹的马格努斯效应进行了理论、试验和数值模拟研究。90年代至今，雷娟棉等[15]对旋转弹进行了大量研究工作，并对火箭弹锥形运动原理进行了分析。此外，西北工业大学[16]、国防科技大学[17]等高校对细长体旋转弹布局也进行了一些研究。

目前，国内外大多数旋转导弹的气动特性研究主要针对自旋运动和鸭舵的俯仰振荡以及它们的耦合情况，而对于锥形运动与自旋运动耦合情况下弹体锥形不稳定性的气动特性研究较少，相关风洞试验技术也处于研发阶段。

耦合运动细长体的数值模拟是指在数值模拟过程中同时实现计算模型的锥形运动和自旋运动，研究其耦合运动下的空气动力学特性。本文在分析耦合运动细长体的空气动力学特性基础上，开展细长体鸭舵诱导涡系结构和尾翼流场特性研究，研究成果可为旋转导弹气动特性和飞行稳定性研究提供理论参考依据，并为相关旋转弹耦合运动风洞试验技术研发提供数据参考。

1　数值计算方法

采用三维可压缩Navier-Stokes方程作为求解方程组，其积分形式为

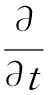
(1)

式中：W为守恒变量；Fc为对流通量；n为控制体边界∂Ω的外法向矢量；Fv为粘性通量。

湍流模型采用重整化(RNG)的k-ε模型，该模型在保持标准k-ε模型高稳健性的基础上，对于具有复杂剪切和高应变率的旋转、分离流动具有较好适应性。计算来流马赫数取1.6，雷诺数取1.8×106.

采用绝热、无滑移壁面边界条件，利用刚性网格运动技术，在非定常计算时气流坐标系固定，模型在给定的攻角下随网格整体做刚性转动。Navier-Stokes方程中对流通量采用2阶迎风Roe格式，时间推进采用基于伪时间步的隐式双时间推进方法，每个旋转周期内为400时间步，内循环时间步为30步。

2　计算模型及网格

本文选取的计算模型为带鸭舵细长体模型，模型全长为2 000 mm，等直段直径为100 mm，长径比为20. 计算模型示意图如图1所示。

计算耦合状态下带鸭舵细长体的气动特性，需要在数值求解过程中同时实现模型的锥形运动和自转运动，其运动形式如图2所示。

如图3所示，将计算网格划分为内部区域和外部区域。内部区域围绕弹体x轴自转产生模型的自转运动，外部区域围绕通过模型旋转中心的气流x轴自转，使模型产生锥形运动。

本文中锥形运动旋转速度为720 °/s，自转运动旋转速度为2 700 °/s. 为了提高气动力的数值模拟精度，计算网格物面第1层y+取1，不使用物面函数，不考虑锥形运动中细长体的弹性变形。

3　定常计算结果分析

定常绕流的计算可以作为非定常计算的初始结果，从而节省计算时间、提高计算准确性。定常计算状态共4个，攻角分别为0°、5°、10°和15°. 图4为定常计算状态下模型升力系数随攻角变化的曲线。从图4中可以看出，升力线斜率线性度良好，符合带鸭舵细长体的气动特性规律。

图5为弹体坐标系Ox轴在鸭舵中心垂面的马赫数等值线图，攻角分别为5°、10°和15°. 由图5可以看出，随着攻角的增加，鸭舵上表面低速回流区的范围逐渐增大，并且鸭舵翼根比翼稍更加明显。在弹体上表面，可以看到15°攻角下的流场形态与前两个攻角明显不同，这是由于攻角为5°和10°时，弹体表面两侧流体沿弹体表面向上流动，在截图位置处汇聚形成低速区；而在15°攻角时，由于弹体阻碍作用增强，不能形成这种汇聚，形成两个低速区并存的现象。此外，随着攻角增大，鸭舵对流体上行的阻碍作用也会逐步增强。

在鸭舵上、下表面一定距离处，马赫数等值线的量值会发生突变。这是由于在超声速来流的作用下，鸭舵前缘会产生弧形脱体激波。随着攻角的增大，激波与鸭舵的相对位置发生变化，使得激波上半部分逐渐远离鸭舵上表面，气流经过激波造成马赫数量值的突变。

图6所示为攻角15°时弹体上表面和鸭舵(靠近翼尖)附近流场的流线图。与前文分析一致，在弹体上表面，由于弹体的阻碍作用，使得弹体两侧绕流的流线没有足够的能量在弹体上表面汇合，形成在两块流线稀疏的区域，即图5中15°攻角鸭舵中心垂面的低速区。从鸭舵附近流线图可以看出，在当前计算状态下，鸭舵上表面形成两个分离涡，但是由于采用定常算法，分离涡并没有继续向下游发展，是直接耗散消失，而在下文的非定常计算中，分离涡将逐渐向下游发展。

4　耦合运动结果分析

利用非定常数值模拟方法可以得到耦合运动下细长体表面复杂涡系流场的变化规律，以及其空气动力学特性随时间的发展趋势。

4.1　气动系数特性分析

图7～图9所示分别为一个运动周期(1.00～2.00 s)内的升力系数、侧向力系数和阻力系数随旋转角的变化曲线，图中采用双横坐标作图方式，上方横坐标为自转运动旋转角，下方横坐标为同一时刻锥形运动旋转角。

对于单纯锥形运动或者单纯自转运动，升力、侧向力和阻力系数随时间(滚转角)的变化曲线整体上是周期性的，但是当两种运动耦合后会使这种周期性变化更为剧烈，图7～图9中每个数据点的量值都是由这两种运动耦合作用导致的，在1个周期内，锥形运动旋转720°，自转运动旋转2 700°，锥形运动改变细长体的攻角和侧滑角，自转运动改变细长体的滚转角，这种耦合运动导致了升力和侧向力系数曲线呈振荡性周期变化，图中数据点上下横坐标对应的位置即为该时刻模型的锥动旋转角和自转旋转角。

图7～图9表明，本文数值计算捕捉到了耦合运动下细长体的主要气动特性。随着起始攻角的增大，细长体锥形运动的迎风作用面增加，促使升力系数和侧向力系数的振荡幅度增加，但是其振荡规律是一致的。当攻角分别为5°、10°和15°时，升力最大值均发生在锥动旋转角为378°、自转旋转角为1 417.5°附近，侧向力最大值均发生在锥动旋转角为475.2°、自转旋转角为1 782.0°附近。由于本文耦合运动的特殊性，升力系数和侧向力系数曲线随时间变化规律基本一致，存在一定的相位差。对于阻力系数，攻角分别为5°、10°和15°时均为周期性变化，振动幅度随攻角的增大而增加。

为了更加清晰地分析锥动和自旋耦合运动的特殊气动性能，图10对比了一个周期内锥动和自旋耦合运动以及单独锥动和自旋运动的升力系数。结合上文分析可知，在锥动和自旋耦合运动中，锥形运动对弹体气动系数曲线的分布起主导作用，但是由于自旋运动的存在，使得耦合运动的升力系数在单独锥形运动曲线发展趋势的基础上呈现出更为复杂的变化。然而，耦合运动的升力系数曲线并不是两种子运动曲线的线性叠加，而是由当前时刻模型的空间位置和姿态决定，例如当耦合运动峰值位置(锥动旋转角为378°、自转旋转角为1 417.5°)时，耦合运动的升力系数为4.46，而锥形运动和自旋运动两种子运动的升力系数分别为4.21和5.41.

4.2　涡系结构分析

带鸭舵细长体的主要涡系结构是鸭舵产生的诱导涡，这些涡是非常复杂的，常常与非定常的激波、膨胀波、边界层相互交互干扰，造成鸭舵诱导涡系结构的不稳定现象。

根据运动情况，选取非定常计算周期T的1.125 s、1.250 s、1.375 s和1.500 s作为涡系结构分析的时间点，在10°攻角时，模型空间运动位置如图11所示，其对应的锥动旋转角分别为90°、180°、270°和360°，自转旋转角分别为337.5°、675.0°、1 012.5°和1 350.0°.

图12所示为不同时刻细长体导弹不同截面处的涡量示意图。从图12中可以看到，模型周围涡系结构随模型空间位置而变化。在特定时刻，鸭舵诱导涡系从鸭舵后缘逐渐向弹体尾部发展，涡系半径逐渐增大。起始攻角的增大，使得流场的非定常效应增强，在一定程度上对鸭舵诱导涡系产生破坏作用，使涡耗散的剧烈程度增加。在不同时刻，来流对迎风面的吹袭作用使得涡系漩涡逐渐向模型背风面移动，并与边界层相互干扰。

当T=1.125 s时，耦合运动使得弹体右侧的分离涡贴近弹体表面，左侧涡系远离弹体表面。当T=1.250 s时，弹体x轴与风轴x轴呈-5°夹角，来流的吹袭作用使得分离涡向气流y轴负方向移动，迎风位置处的部分涡系结构被来流破坏。T=1.375 s与T=1.125 s时的情况基本相同，但是由于自转旋转角度的区别，使得鸭舵相位角不同，从而导致涡系结构的差异，两时刻模型侧滑角完全相反，导致涡系偏离方向几乎相反。当T=1.500 s时，来流使得分离涡向气流y轴正方向移动，弹体x轴与风轴x轴呈5°夹角，下鸭舵诱导涡基本被破坏，上鸭舵诱导涡由于弹体对来流的阻挡作用得以部分保存。

从图12的涡系结构来看，弹体的涡系结构与气动系数变化是相互对应的。锥形运动的攻角效应总体上决定了周期运动的频率，而自转运动涡系结构演化过程决定了周期运动变化的剧烈程度。在同一时刻，随着攻角效应的增大，涡系结构变得更加不稳定，与附面层和来流的干扰更加明显，鸭舵分离涡的不断破裂造成气动系数曲线的振幅更加剧烈。对于单纯自旋运动，涡系结构的生成与破裂在自旋周期内是周期性的，但是由于锥形运动的存在，使得在一个自转周期内耦合运动涡系结构的生成与破裂出现延缓或者加速，从而造成气动系数在一个耦合周期内振荡程度的不同。

4.3　尾翼流场分析

图13～图15是不同起始攻角下1.125 s、1.250 s、1.375 s和1.500 s时刻尾翼中弦线的压力系数等值线前视图。由图13～图15中可以看到，模型的旋转运动带动附近气流旋转、产生环流，使得弹翼周围形成一个非对称环状压力等值线圈。

在不同时刻的压力等值线图中，基本上都出现了4个高压区域，这是由于弹翼周围形成了楔形激波，流体穿过激波后压力升高造成的。当T=1.125 s时，锥动旋转角度为90°，自转旋转角度为337.5°，模型处于5°侧滑角的位置，此时从细长体前方观察，弹体左侧属于迎风面，因此该侧弹翼激波强度较大，形成的高压区域也比较明显。其他时刻的分析规律相同。

与鸭舵同样，在超声速来流的作用下，弹体尾翼同样会产生脱体激波。处于弹体迎风面一侧的尾翼激波强度较强，处于背风面的激波强度最弱，且相邻尾翼激波系出现交汇现象，从而在尾翼中弦线截面图中形成不同范围的高压区域。

随着起始攻角的增大，相同时刻下的高压区域逐渐向弹身靠近，这是由于激波位置随攻角而变化造成的。从翼尖开始，由于尾翼外围的压强大于翼根处的压强，使得4片弹翼附近均出现明显的加速区，并且不同攻角下的加速区范围不同。

5　结论

本文通过数值模拟得到了定常和耦合运动下细长体导弹的空气动力学特性，通过对不同运动情况下细长体导弹的涡系结构、流场结构以及气动数据特性分析，得到以下结论：

1) 自转和锥动耦合运动下，细长体气动力系数曲线振动峰值只与运动起始攻角有关，与旋转速度无关。锥形运动对弹体气动系数曲线的分布起主导作用，自旋运动使得曲线发展规律更为复杂。

2) 鸭舵诱导产生的分离涡与边界层之间互相干扰、相互融合，涡系发展情况更为复杂。来流会造成涡系漩涡向模型背风面移动，并对涡系结构造成不同程度的破坏，攻角的增大会加剧涡系结构对边界层的影响。

3) 弹体旋转作用会使弹翼周围形成一个非对称环状压力等值线圈，在弹体迎风面形成较明显的高压区域，且随着攻角的增大，高压区域逐渐向弹身靠近。

4) 高速耦合旋转运动下，弹体气动力发展规律复杂，幅值变化剧烈，对于旋转弹锥形稳定性控制极为不利，严重影响着导弹命中精度。

参考文献(References)

[1]Curry W H, Reed J F. Measurement of Magnus effects on a sounding rocket model in a supersonic wind tunnel[C]∥Proceedings of the 2nd Aerodynamic Testing Conference.Los Angeles,CA，US: AIAA,1966: 754.

[2]Liano M G. Stability analysis and fight trials of a clipped wrap around fin configuration[C]∥AIAA Atmospheric Flight Mechanics Conference and Exhibit. Rhode Island,US:AIAA,2004.

[3]Regan F L, Shannon J H W, Tanner F J. The joint NOL/RAE/WRE research program on bomb dynamics. Part IV. A low-drag bomb with freely spinning stabilizers，AD074785[R].White Oak, ML, US: Naval Ordnance Laboratory, 1973:1-39.

[4]Tisserand L E. Aerodynamics of a rolling airframe missile,ADA111769 [R].Baltimore,Maryland, US: the Johns Hopkins University/Applied Physics Laboratory,1982:125-147.

[5]Gold R, Busan R. Design and implementation of a full-scale spinning missile model with active canard control[C]∥32nd Aerospace Sciences Meeting and Exhibit.Reno,NV,US: AIAA, 1994.

[6]Dilley A D, Mcbride R T,Yuli V A. Dynamic wind tunnel test of an innovative rolling missile mode[C]∥26th AIAA Aerodynamic Measurement Technology and Ground Testing Conference. Seattle, Washington, US:AIAA,2008.

[7]Burkhalter J E, Heiser M A.Linear aerodynamic analysis of a supersonic spinning missile with dithering canards[C]∥20th AIAA Applied Aerodynamics Conference. St. Louis, MI，US:AIAA, 2002.

[8]Heiser M. Linear aerodynamic analysis of a spinning missile with dithering canards[C]∥20th AIAA Applied Aerodynamics Conference. St. Louis, MI，US:AIAA, 2002.

[9]Murman S M,Aftosmis M J,Berger M J. Numerical simulation of rolling-airframes using a multi-level Cartesian method[C]∥20th AIAA Applied Aerodynamics Conference. St. Louis, MI，US:AIAA,2002.

[10]Nygaard T A,Meakin R L. Aerodynamic analysis of spinning missile with dithering canards[J]. Journal of Spacecraft and Rockets,2004,41(5):726-734.

[11]Blades E L, Marcum D L . Numerical simulation of a spinning missile with dithering canards using unstructured grids[J]. Journal of Spacecraft and Rockets,2004,41(2):248-256.

[12]Sheng C H,Wang X. Aerodynamic analysis of a spinning missile with dithering canards using a high order unstructured grid scheme[C]∥Proceedings of the 47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Orlando, FL, US:AIAA,2009.

[13]Sheng C H, Wang X, Zhao Q Y. Aerodynamic analysis of a spinning missile using a high-order unstructured-grid scheme[J]. Journal of Spacecraft and Rocket,2010,47(1):81-89.

[14]苗瑞生，吴甲生．旋转弹空气动力学[J]．力学进展,1987，17(4):497-488．

MIAO Rui-sheng， WU Jia-sheng． Aerodynamics of spinning projectiles[J]． Advances in Mechanics，1987，14(4): 479-488．(in Chinese)

[15]雷娟棉，吴甲生.尾翼稳定大长径比无控旋转火箭弹的锥形运动和抑制[J].空气动力学学报,2005，23(4): 455-457.

LEI Juan-mian, WU Jia-sheng. Coning motion and restrain of large fineness ratio unguider spinning rocket stabilized with tail fin[J]. Acta Aerodynamica Sinica，2005，23(4): 455-457. (in Chinese)

[16]薛帮猛，杨永．旋转弹丸马格努斯力数值计算[J]．弹箭与制导学报，2005，25(2): 85-87．

XUE Bang-meng，YANG Yong． Numerical calculation of Magnus force acting on spinning projectile[J]． Journal of Projectiles, Rockets, Missiles and Guidance，2005，25(2): 85-87．(in Chinese)

[17]王智杰，陈伟芳，李浩．旋转弹丸空气动力特性数值解法[J]．国防科技大学学报，2003，25(4): 15-19．

WANG Zhi-jie，CHEN Wei-fang，LI Hao． Numerical solution of the aerodynamic projectiles of the rotating projectiles[J]. Journal of National University of Defense Technology，2003，25(4): 15-19．(in Chinese)