基于改进粒子群算法的进线档导线相间距离计算分析
陆 彬, 赵新宇, 张瑞永,马 军, 朱 源
(中国能源建设集团江苏省电力设计院有限公司,江苏 南京 211102)
0 引言
在高压输电线路中,变电站构架出线方式一般采用三相水平排列,而常规高压铁塔型采用三相垂直排列方式。因此,三相导线从水平排列过渡到垂直排列,在三维空间上出现交叉现象,在档距、高差、张力等多重因素作用下,进线档相邻相的最近距离有可能不满足规程规范要求。若不及时在设计阶段进行校验分析,将会对施工和竣工验收造成严重的进度影响和经济损失[1-5]。
目前求取空间相导线间的最近距离常用的方法有:(1) 把弧线简化成直线,近似求解两条直线间的最近距离,这种计算方法存在较大误差[6];(2) 建立相导线的斜抛物线计算公式,按固定步长在斜抛物线上选取有限数量的点,逐点穷举计算,直至计算出最近距离[7-8]。这种计算方法的精度取决于固定步长的大小,且较难计算出准确的最近距离。
针对目前相间距离校验困难等问题,本文基于在三维空间中建立的相导线斜抛物线的计算模型,采用改进粒子群算法实施全局搜索策略,智能快速收敛于最优解,在确保计算精度的同时缩短计算时间。本文还分析了相邻相的最小相间距离与档距、相导线张力、挂点高差的变化关系。
1 斜抛物线的三维空间计算模型
定义以线路中心线为X轴方向,中心线左右两侧为Y轴方向,高程为Z轴方向。定义构架挂点坐标为(X0,Y0,Z0),杆塔挂点坐标为(X1,Y1,Z1)。相导线上任意一点辅助档距为ΔL。
则相导线两端挂点直连线上任意一点的空间坐标(X′,Y′,Z′)表达式为[9-10]:
(1)
(2)
在计算过程中,架空线均假设为无刚性的柔性索链,悬链线上任意一点的弧垂表达为[11-14]:
(3)
式中:T为相导线张力;g为导线的荷载;β为链线两端的高差角。
若设θ为导线的风偏角,则悬链线上任意一点的空间坐标为:
(4)
2 相间距离的合格距离数学模型
根据现有文献资料[9,15-16]及国内外线路的运行经验,操作过电压决定水平线间最小电气间隙距离。对文献公式进行修正后,进线档相邻相导线的最小距离表示为式(5):
(5)
式中:U为线电压;f1和f2为相邻两相导线最近点的实际弧垂;f1max和f2max为相邻两相导线的最大弧垂。
3 改进粒子群算法
3.1 改进粒子群算法介绍
粒子群优化算法(particle swarm optimization,PSO)是一种进化计算技术,由Eberhart博士和Kennedy博士发明[17]。PSO同遗传算法类似,是一种不断迭代寻求最优目标的计算工具,PSO适合求解连续非凸性问题。
数学描述为:d维目前搜索空间中的第i个微粒的位置和速度分别表示为Xi=[xi1,xi2,…,xij]和Vi=[vi1,vi2,…,vij]。在每一次迭代中,评价各微粒的目标函数,确定t时刻每个微粒所经过的最佳位置pbest以及群体所发现的最佳位置gbest,通过跟踪这两个最佳位置按照式(6)、(7)分别更新微粒的速度和位置,直至迭代步数结束[18]。为确保收敛到全局最优,公式中引入惯性权重系数w。
vi,j(t+1)=wvi,j(t)+c1r1[pi,j-xi,j(t)]+
c2r2[pg,j-xi,j(t)]
(6)
xi,j(t+1)=xi,j(t)+vi,j(t+1)j=1,2,…d
(7)
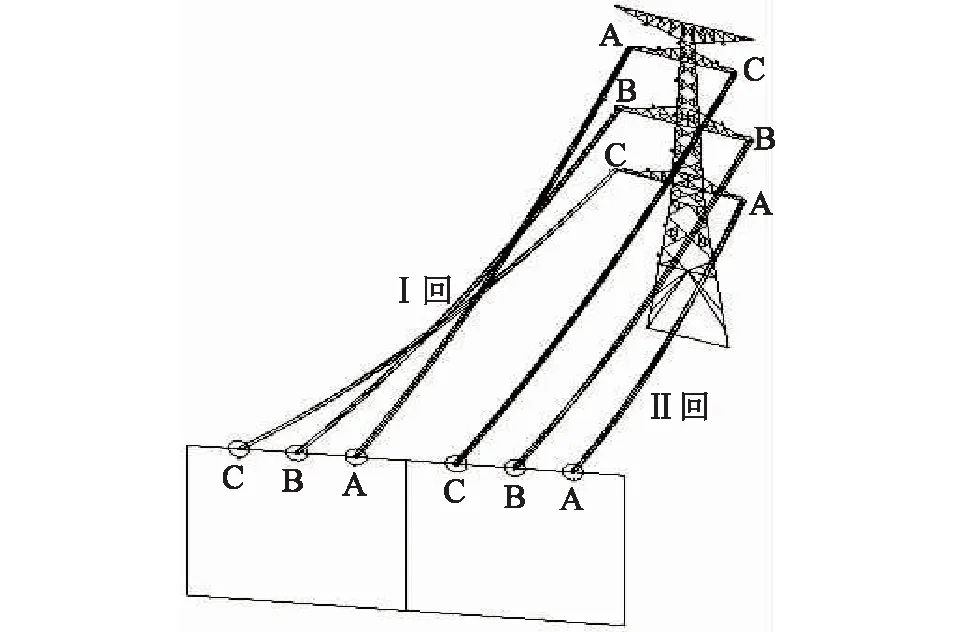
式中:pi,j为自身最佳位置;pg,j为群体最佳位置;c1和c2为正的学习因子;r1和r2为0到1之间均匀分布的随机数。
3.2 改进粒子群算法步骤
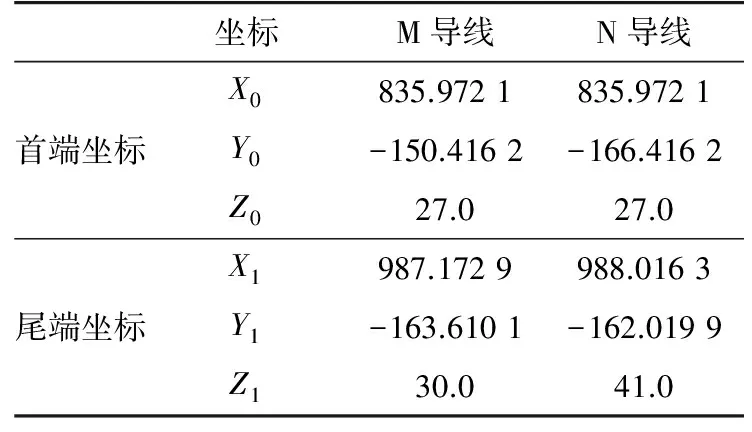
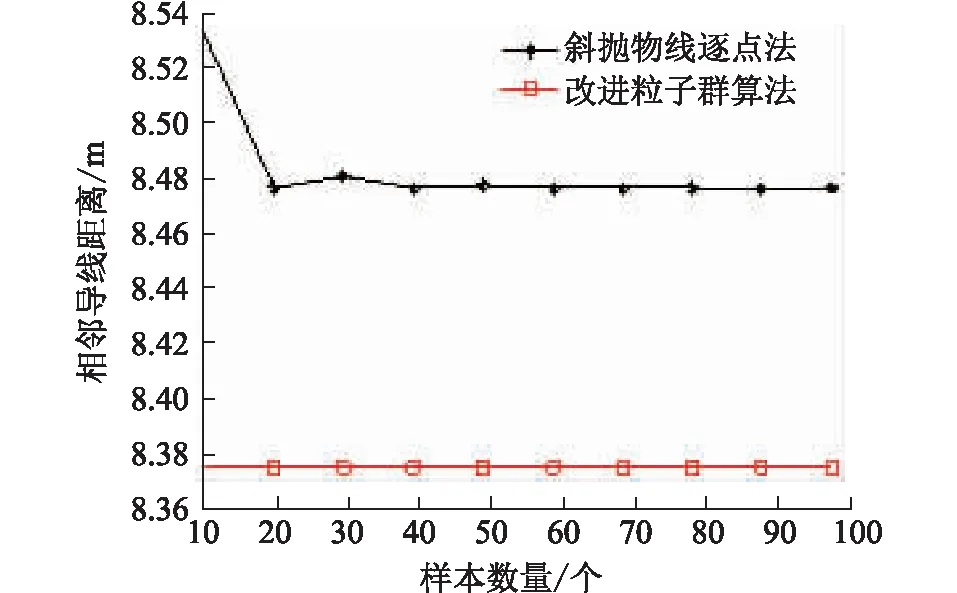
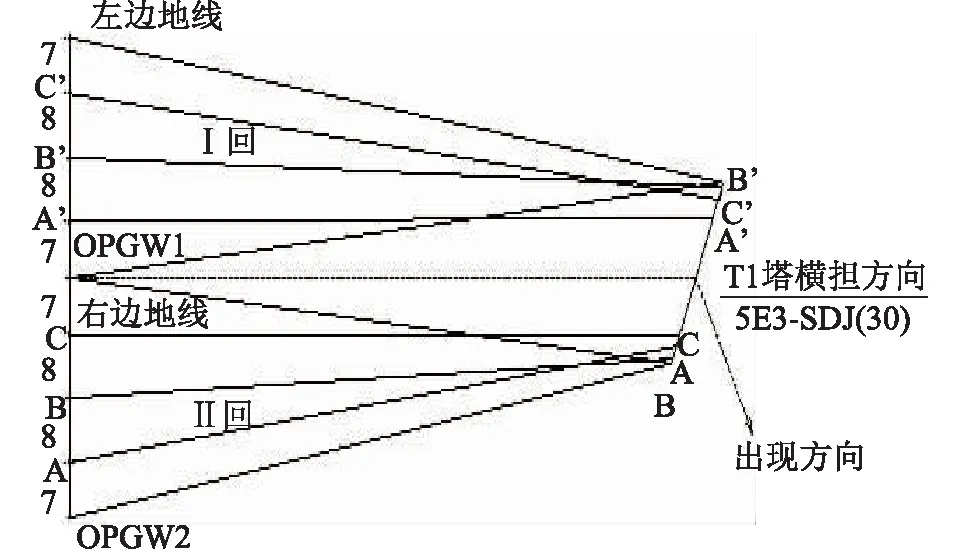
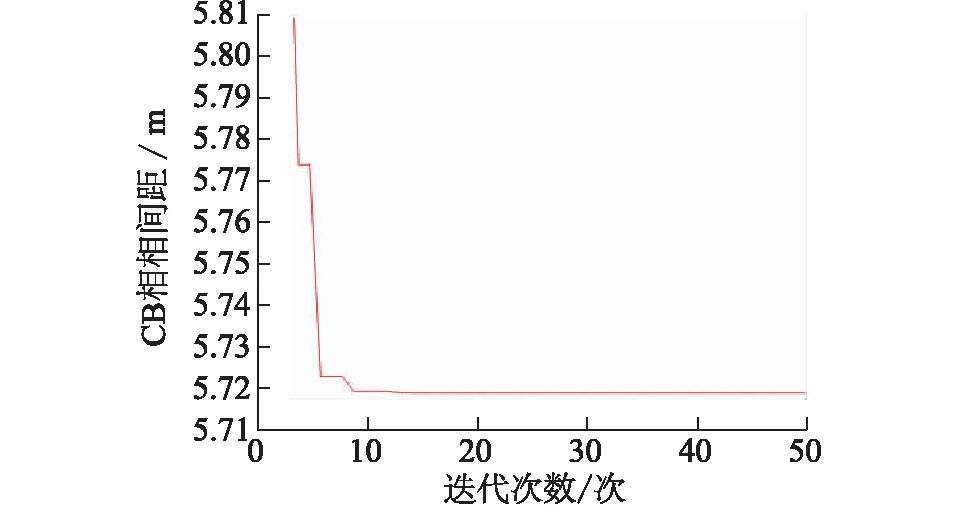
根据第二节建立的相导线悬链线坐标计算模型,采用粒子群算法进行相导线距离计算时,先分别随机设定三维空间中A、B、C三相X轴的第i个粒子的位置和速度,分别为ti=[t1,t2,t3]i和Vi=[v1,v2,v3]i,其中变量ti为A、B、C三相各相的ΔL/L值,约束条件为0 步骤1:初始化A、B、C相上的点的速度和位置。根据这些初始化点计算相邻相导线距离,并将相邻相最近距离的点(XABC,YABC,ZABC)设为初始位置pbest,相对应的t值设为最优值gbest。 步骤2:进入主循环。计算每个微粒的目标函数值,例:计算A,B相导线距离。 步骤3:根据更新方程式(6)、(7)来调整三维空间中A、B、C三相X轴的速度和位置,从而更新相导线最优位置坐标(XABC′,YABC′,ZABC′)。 步骤4:计算微粒更新后每个位置的适应度,将每个位置的新的f与其以前经历过的最好位置pbest所对应的f比较,如果好,则替代原来的pbest。 步骤5:将每个微粒的适应度与全体微粒所经历过的最好位置gbest比较,如果好,更新gbest。 步骤6:检查终止条件,如果满足迭代次数,停止迭代,否则返还步骤3。 假设某两根M、N导线首尾挂点的三维空间坐标如表1所示。 表1 M和N导线挂点三维空间坐标Tab.1 Hanging points of M,N wire in 3d space coordinates 改进粒子群算法计算精度与粒子数有关,而斜抛物线逐点法精度与导线上所选点的个数有关。文中把粒子群算法的粒子数与斜抛物线逐点法平均取点数视为等价,即样本数等价。2种计算方法如图1所示:随着样本数的增加,斜抛物线逐点法计算值趋于稳定,但是仍然有波动,这是因为平均取点无法正确取到最优点(有可能跳过最优点),而改进粒子群算法在样本数为10时,计算结果就已经取到最优值。计算精度比斜抛物线逐点法高1.22%,体现了改进粒子群算法的优越性。 图1 2种计算方法结果的曲线Fig.1 The results of Two kinds of calculation method 某500 kV配套送出工程进线档,构架挂点高度为27 m,终端塔型号为5E3-SDJ(30),杆塔转角为右转55°53′02″,进线档档距146 m。导线采用钢心高导电率铝绞线4×JL3/G1A-630/45,相导线最大使用张力为80 kN。进线档的俯视图和立体图如图2、图3所示。 图2 进线档俯视图Fig.2 Vertical view of transmission line 图3 进线档立体图Fig.3 Stereogram view of transmission line 本文以第Ⅰ回作为计算对象。根据工程实际情况,变电站构架侧相序不变,终端塔一侧相序自下而上有6种排列方式。本文分别对这6种排列方式采用改进粒子群算法计算相邻相的相间距离,并进行校核。改进粒子群算法中粒子数取40,学习因子取2,最大权重系数取0.9,最小权重系数取0.4,迭代步数取200。结果如表2所示。由表2看出,Ⅰ回线路自下而上的排列方式只有BCA和ACB满足最小距离要求,其余均不合格。 表2相间距离计算 相序排列方式最危险两相/相间距合格距离结论CBACB/5.4155.634不合格CABAB/5.0845.598不合格BCABC/6.3175.575合格BACBA/5.4215.636不合格ABCBC/5.0475.599不合格ACBBA/6.7165.088合格 如果以第一种自下而上排列方式CBA为例,把C相的最大使用张力降到70 kN,结果如表3所示。由表3可知,C相张力放松后,C相的弧垂变大,相邻相的相间距离均能满足规程规范要求。 表3CBA排列方式C相放松计算 相邻相相间合格距离结论CB5.7195.656合格BA6.9735.334合格AC13.3055.589合格 图4为采用改进粒子群算法计算时,C、B相间距离随迭代次数增加的变化曲线。由图4看出,迭代次数为10次时,C、B相间距离已基本收敛到最近距离5.719 m,计算效率很高。 图4 相间距改进粒子群算法的适应度曲线Fig.4 Fitness curve of phase distance based onimproved PSO algorithm 进线档相邻相的相间距离计算与档距、张力、高差等都有直接的因素。文中针对上述工程自下而上相序排列方式为CBA作为算例,着重定量仿真计算C、B两相最小相间距离与相关敏感因素的关系。 除特殊说明外,最小相间距离计算条件为:构架挂点高度为27 m,终端塔型号为5E3-SDJ(30),杆塔转角为右转55°53′02″,进线档档距146 m,相导线最大使用张力为80 kN。 控制条件:档距从30 m至150 m变化。 由图5可知,随着档距的增加,在档距30 m至80 m时,C、B两相的最小相间距离增加较快,随后增加趋势变缓。档距小于115 m时,最小相间距离曲线始终在合格相间距离曲线之上,该档距内架线均能满足规程规范要求。档距大于115 m时,C、B最小相间距离曲线在合格相间距离曲线之下。 图5 最小相间距随档距的变化曲线Fig.5 The change curve of the minimum phase distance with the increasing of span 控制条件:C相张力从40 kN至120 kN的变化。 由图6可以看出,随着C相导线的张力变大,C、B两相的最小相间距离逐渐减少,而C、B两相的合格距离变化不大。C相导线张力增加到约72 kN时,两条曲线相交,随着张力继续增大,C、B最小相间距离曲线在合格相间距离曲线之下,无法满足规程规范要求的安全距离。此图C、B两相最小相间距离与C相张力的关系准确验证了第四节中实际工程算例结果。 图6 最小相间距随张力的变化曲线Fig.6 the change curve ofthe minimum phase distance with the increasing of tension 控制条件:构架挂点高度不变,终端塔呼高从18 m至48 m变化。 图7 最小相间距随挂点高差的变化曲线Fig.7 The change curve of the minimum phase distance with the increasing of height 由图7可以看出,随着终端塔的呼高增大,C、B两相的最小相间距离迅速减小,而C、B两相的合格相间距离缓慢增加,在呼高约为39 m时,两曲线相交。可以看出在该计算条件下,呼高39 m是满足相间距离安全的极限呼高值。 文中对进线档相导线的任意一点建立三维数学模型,通过改进粒子群算法准确快速地计算工程样例中相邻相最小相间距离。文中详细研究了最小相间距离与档距、相导线张力、和挂点高差的关系。通过数学分析和MATLAB仿真模拟科学解释了工程算例的计算结果得到以下结论: (1) 随着档距的增加,相邻两相的最小相间距离增加较快,随后增加趋势变缓。合格相间距离随档距的增大基本成线性增加。存在一个临界档距,当小于该临界档距时,最小相间距离均满足合格距离要求,反之不满足。 (2) 随着某一控制相的导线张力变大,相邻两相的最小相间距离逐渐减少,而合格距离变化不大。控制相导线存在一临界张力,当张力小于该临界值时,最小相间距离均满足合格距离要求,反之不满足。 (3) 随着终端塔的呼高增大,相邻两相的最小相间距离迅速减小,而合格相间距离缓慢增加。构架挂点高度固定时,终端塔存在一临界呼高值,当呼高小于该临界值时,最小相间距离均满足合格距离要求,反之不满足。 参考文献: [1] 王川化,余鹏飞. 一种基于可靠性分析的输电线路路径设计方法[J]. 电力工程技术,2017,36(5):79-84. WANG Chuanhua,YU Pengfei. A transmission line path design method based on reliability analysis[J]. Electric power engineering technology,2017,36(5):79-84. [2] DL/T837—2010 输变电设施可靠性评价规程[S]. 北京:中国电力出版社,2012. DL /T837—2010 Reliability evaluation code for transmission and distribution installation[S].Beijing:China Electric Power Press,2012. [3] 赵鹏程. 输电线路设计工程的路径选择及质量控制[J].广东科技,2009(18):217-219. ZHAO Pengcheng. Path selection and quality control of transmission line design engineering[J]. Guangdong science & technology,2009(18):217-219. [4] 汪晶毅,朱映洁,潘春平. 国内外架空输电线路电气间隙设计对比[J]. 广东电力,2016,29(12):127-134. WANG Jingyi, ZHU Yingjie, PAN Chunping. Designs comparison for electric clearance of overhead transmission lines between domestic and abroad criteria[J]. Guangdong Electric Power,2016,29(12):127-134. [5] 谢云云. 适用于有高差线路的输电导线ANSYS找形方法[J]. 电力工程技术,2017,36(2):30-35. XIE Yunxun. Form-finding method of transmission lines consulting the lowest point[J]. Electric Power Engineering Technology,2017,36(2):30-35. [6] 杨振谷. 对线路相间距离最小值求解的讨论[J]. 电力建设,1993,14(11):31-33. YANG Zhengu. The discussion of the minimum distance and of the line[J]. Electric Power Construction,1993,14(11):31-33. [7] 柏晓路,葛秦岭,余雯雯,等. 架空输电线路最小相间距离计算分析 [J]. 电力科学与工程,2010,26(4):37-40. BAI Xiaolu,GE Qinlin,Yu Wenwen,et al. Analysis of phase distance of transmission line[J]. Electric Power Science and Engineering,2010,26(4):37-40. [8] 刘亚威,张雪萍,杨腾飞. 基于量子粒子群优化的最优障碍路径分析[J]. 电子设计工程,2011,19(12):15-17. LIU Yawei,ZHANG Xueping,YANG Tengfei. Analysis of obstacle optimal path based on quantum particle swarm optimization[J]. Electronic Design Engineering ,2011,19(12):15-17. [9] 杨晓梅,冯宁,吴锁平,等. 基于三维空间技术的进线档导线相间距离精确计算[J]. 电力建设,2012,33(10):46-49. YANG Xiaomei,FENG Ning,WU Suoping,et al. Precise calibration for phase distance of approach span based on three-dimensional space technology[J]. Electric Power Construction,2012,33(10):46-49. [10] 姚吉利. 三维坐标转换参数直接计算的严密公式[J]. 测绘通报,2006(5):7-10. YAO Jili. Rigorous formula for calculation parameter in 3D transformation[J]. Surveying and Mapping,2017,36(2):30-35.,2006(5):7-10. [11] 王亦清,朱宁西,孙鹏,等. 计及空间相关性的架空线路载流量预测方法[J]. 广东电力,2017,30(10):6-10 WANG Yiqing, ZHU Ningxi, SUN Peng, et al. Prediction method for carrying capacity of overhead transmission line measuring spatial correlation[J]. Guangdong Electric Power,2017,30(10):6-10. [12] 龚宇清,梁宁川,龚永光. 架空送电线路导线电气距离的公式计算方法[J]. 电力建设,2009,30(7):24-27. GONG Yuqing,LIANG Ningchun,GONG Yongguang. Analysis of the electric distance of transmission line[J]. Electric Power Construction,2009,30(7):24-27. [13] 张殿盛, 龚永光. 电力工程高压送电线路设计手册[M]. 北京:中国电力出版社,2003,181-182. ZHANG Diansheng,GONG Yongguang. High voltage power transmission line design manual for power engineering[M]. Beijing:China Electric Power Press,2003,181-182. [14] 孟遂民,孔伟. 架空输电线路设计[M]. 北京:中国电力出版社,2007,56-100. MENG Suimin,KONG Wei. Design of high voltage transmission[M]. Beijing:China Electric Power Press,2007,56-100. [15] GB 50545—2010 110~750 kV架空送电线路设计技术规程[S]. 北京:中国电力出版社,2010. GB 50545—2010 Code of design of 110 ~750 kV overhead transmission line[S]. Beijing:China Electric Power Press,2010. [16] KENNEDY J,EBERHART R. A discrete binary version of the particle swarm algorithm[J]. Proceeding of the Word Multiconference on Systemics,Cybernetics and Informaties,New Jersy,Piscataway,1997:4104-4109. [17] 龚纯,王正林. 精通MATlAB最优化计算[M]. 北京:电子工业出版社,2009:270-275. GONG Chun,WANG Zhenglin. Proficient in MATlAB optimization calculation[M]. Beijing:Electronic Industry Press,2009:270-275. [18] 高飞. MATLAB智能算法超级学习手册[M]. 2014,250-260. GAO Fei. MATLAB super learning manual[M]. 2014,250-260. [19] 赵菲,焦彦军. 基于粒子群算法的输电线路参数辨识[J]. 陕西电力,2011(5):30-34. ZHAO Fei,JIAO Yanjun. Probe into parameters identification for transmission lines based on particle swarm optimization algorithm[J]. Shaanxi Power,2011(5):30-34.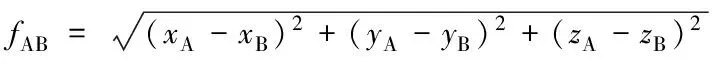
4 工程案例计算分析
4.1 改进粒子群算法与斜抛物线逐点法比较
4.2 进线档相间距离工程实例分析
Tab.2Consideration of phase distance of transmission linem m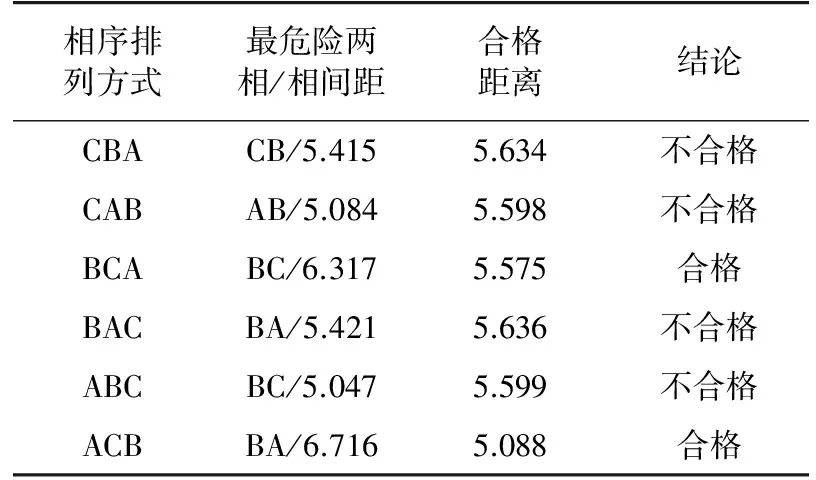
Tab.3Relax consideration of C phase distance m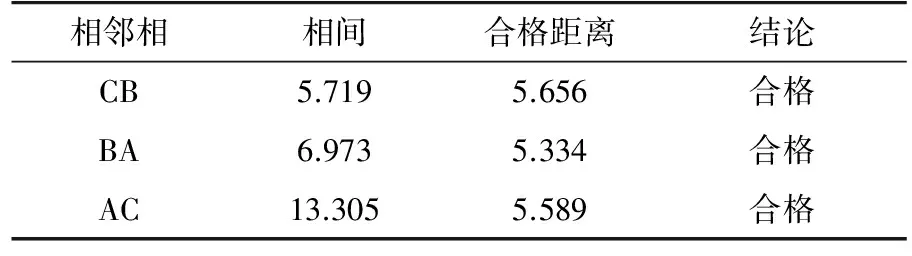
5 敏感因素分析
5.1 进线档档距
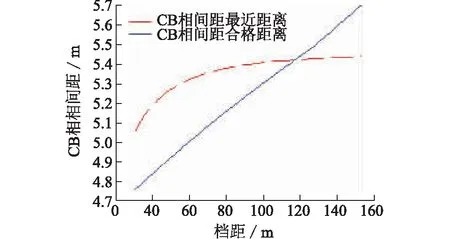
5.2 控制相张力
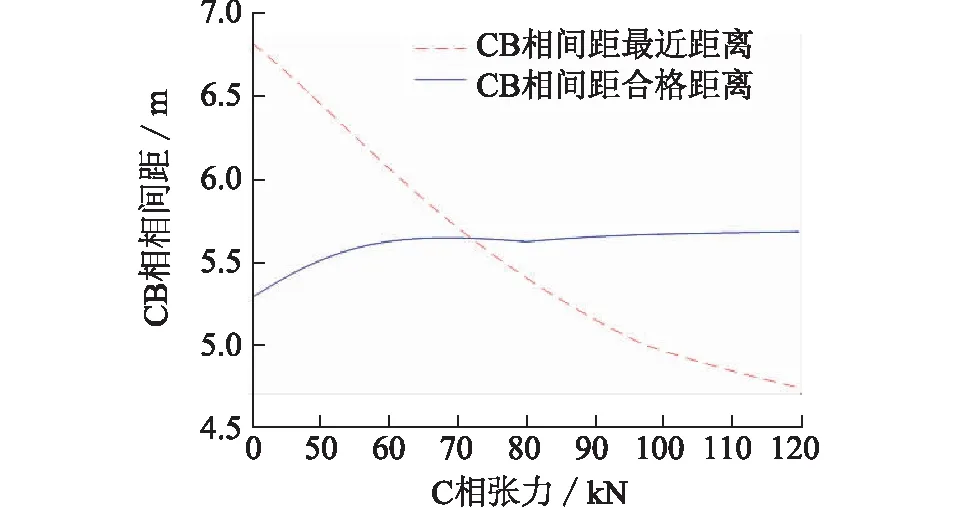
5.3 挂点高差
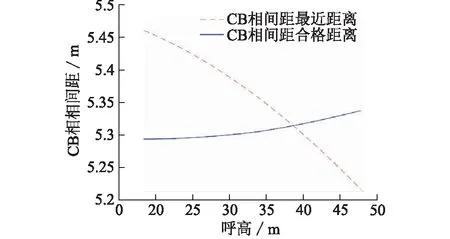
6 结论

