计及DG出力相关性的孤岛微电网蒙特卡洛法概率潮流
苏凯森, 杨家豪, 郑泽蔚, 弓新月
(1. 厦门大学嘉庚学院,福建 漳州 363105;2. 江苏省电力有限公司电力科学研究院, 江苏 南京 211103)
0 引言
近年来,微电网(microgrid,MG)技术得到快速发展[1-2],其离网孤岛运行的能力大大提高了供电可靠性,且对于海岛、偏远地区等,孤岛型微电网也成为了解决供电问题的有效方案。由于无平衡节点,缺乏主网支撑,通常孤岛型微电网采用对等控制方式[3],即通过采取下垂控制策略的分布式电源(distributed generator,DG)、储能装置(energy s ̄t ̄o ̄r ̄age,ES)等共同参与微电网的频率与电压的调节。
诸如光伏、风电这一类DG的出力具有较强的随机性,同时负荷也存在波动,对微电网的频率及电压质量造成影响,而孤岛微电网的潮流计算是分析基础。文献[4—8]建立了孤岛微电网的潮流模型,其中文献[6—7]基于信赖域算法提高潮流计算收敛性,文献[8]提出类奔德斯分解方法较好地提升潮流收敛速度。但对于单一运行点的潮流结果,并未能对微电网频率及电压在不确定性条件下可能的状态提供充分的信息。相比之下,概率潮流(probabilistic load flow,PLF)能够获得各状态变量的完整概率分布信息,更为全面地反映微电网可能的运行状态[9-13]。目前关于孤岛微电网PLF的研究较少,在现有研究中蒙特卡洛模拟法[11]是求解PLF的常用方法。文献[12]采用蒙特卡洛法模拟间歇性微电源的随机特性,从而求解微电网PLF。文献[13]基于半不变量法求解孤岛微电网PLF,计算时将柴油发电机视为平衡节点,储能视为恒功率负荷,相当于采取主从控制模式,由平衡节点承担全部功率波动,不符合实际孤岛微电网的运行特点。
上述文献存在2方面不足:(1) 均未考虑对等控制模式下的孤岛微电网的情况,即仍是默认频率为额定值,只考察系统中电压的概率分布情况。实际中频率是孤岛微电网PLF中重要的待求随机变量,频率的概率分布信息对微电网运行决策提供重要的参考依据;(2) 鉴于微电网属于独立小型系统,微电网中多个光伏电源或风电机组邻近,其出力往往具有较强的相关性,需要在孤岛微电网PLF中计及相关性的影响。
本文的主要贡献是提出一种计及DG出力相关性的孤岛微电网蒙特卡洛概率潮流计算方法。首先简化孤岛微电网节点分类,建立孤岛微电网功率方程;其次建立各类DG及负荷的概率模型,并提出DG出力相关性的处理方法,通过蒙特卡洛模拟计算孤岛微电网PLF;最终通过Benchmark 0.4 kV低压微电网作为算例对文中方法进行验证。
1 孤岛微电网潮流计算
目前孤岛微电网潮流模型中的等效节点类型通常为:PQ节点、PV节点及下垂节点。当出现越限或设备故障脱网时节点类型可能变化,为简化节点分类、减少节点类型转换,同时提高计算效率,文中仅设定PQ节点与PV节点2种节点类型,并建立统一的节点功率方程。
1.1 潮流方程
PQ节点需列写有功与无功平衡方程,PV节点仅需列写有功平衡方程,方程形式为:
(1)
式中:PCi,QCi分别为节点i恒功率电源注入的有功和无功,例如光伏、风电等采取最大功率点跟踪(maximum power point tracking,MPPT)控制方式的DG属于此类电源;PDi,QDi分别为节点i具有下垂控制特性的设备注入的有功和无功,例如柴油发电机、燃气轮机、储能等均属于此类电源;PLi,QLi分别为节点i的有功与无功负荷;Pi,Qi分别为节点i注入的总有功功率和无功功率。
节点注入的有功与无功功率为:

(2)
式中:n为节点数目;Ui及Uj分别为节点i与节点j的电压;Gij,Bij分别为节点导纳矩阵的实部与虚部;δij为节点i和节点j的相角差。
1.2 下垂控制设备建模
具有下垂控制特性的设备注入的功率可统一表示为:
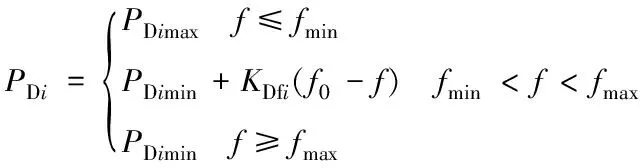
(3)
(4)
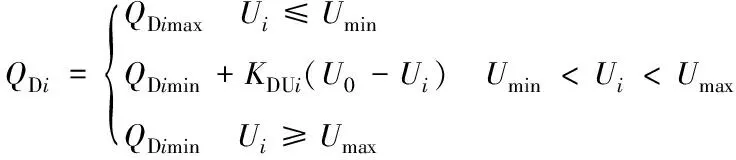
(5)
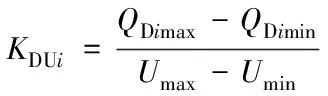
(6)
式中:PDimax,PDimin,QDimax,QDimin分别为节点i具有下垂控制特性的设备注入的有功和无功上下限,若无此类设备则均取为0;fmax,fmin,Umax,Umin分别为系统频率、电压允许上下限;KDfi,KDUi分别为对应的P-f、Q-U下垂系数;f0,f分别为系统频率的空载值与实际值;U0,Ui分别为电压的空载值与实际值。其中储能可以工作在充放电2种工况,在不考虑荷电状态的情况下,其PDimin,PDimax取决于储能的最大充放电功率。
1.3 负荷建模
对负荷进行建模时计及负荷的电压和频率静特性,负荷使用恒阻抗、恒电流和恒功率的组合模型来描述,可表示为:
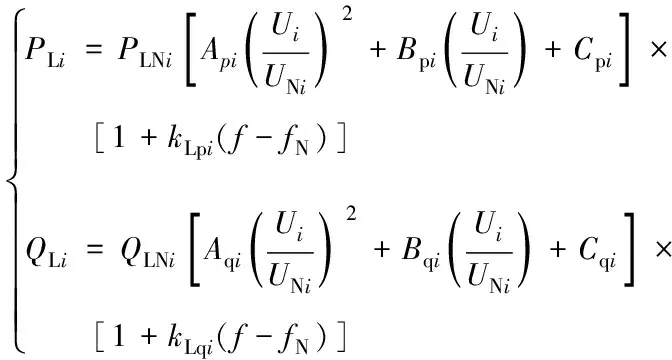
(7)
式中:PLNi,QLNi分别为节点i在额定工况下的有功与无功负荷;UNi和fN分别为额定电压与频率,取UNi=1 p.u.,fN=1 p.u.;Pi,Qi分别为节点i注入的总有功功率和无功功率;Api,Bpi,Cpi,Aqi,Bqi,Cqi分别为负荷有功与无功功率中恒阻抗型、恒电流型、恒功率型的百分比系数,分别满足Api+Bpi+Cpi=1及Aqi+Bqi+Cqi=1;kLpi,kLqi分别为负荷的有功和无功功率的静态频率调节系数。
1.4 潮流求解
假定孤岛微电网中PQ节点与PV节点的数目分别为nPQ与nPV,则总计列写2nPQ+nPV个方程,本文采用牛顿拉夫逊法求解潮流方程组,修正方程简写为:

(8)
式中:ΔP,ΔQ为节点有功与无功不平衡量;Δf,Δδ,ΔU为分别为频率、相角、电压的修正量;J为雅克比矩阵,其分块矩阵分别为:

(9)
由于求解过程中不涉及节点类型转换,因此也无需在迭代过程中改变雅克比矩阵的结构,只需相应更新数值,因此能够为蒙特卡洛模拟提高运算效率。
2 孤岛微电网概率潮流
2.1 蒙特卡洛法概率模型
光伏电源、风电机组为了能在每一时刻尽可能输出最大功率,通常采取MPPT的控制方式,因此DG出力随着光照与风速的随机性也呈现不确定性,而负荷同样存在波动,故而孤岛微电网概率潮流计算中具有随机性的输入变量主要是间歇性DG以及负荷。文中分析涉及的间歇性DG装置为光伏电源(photovoltaic,PV)及风力发电机(wind turbine,WT)装置,文中假设PV与WT均不发出无功。
研究表明,一段时间内的光伏出力满足Beta分布,因此光伏发电有功出力PPV的概率模型以Beta分布来近似表达:
(10)
式中:Γ为Gamma函数;α,β为Beta分布的形状参数;Pmax为该时段内光伏出力最大值。
风速概率分布通常满足Weibull分布,因此风力发电有功出力PWT的概率模型表示为:
(11)
式中:k为形状参数;c为尺度参数;a,b为与WT参数有关的常数。
负荷的概率模型用正态分布描述,其有功和无功功率的概率模型为:

(12)

(13)
式中:μP,μQ分别为有功和无功的均值;σP,σQ分别为有功和无功的标准差。
2.2 DG出力相关性处理
已知m个输入随机变量W=[w1,w2,……,wm]的边际概率分布F(W),并使用相关系数矩阵RW描述出力相关性,相关系数矩阵表达式为:
(14)
矩阵中各元素按下式计算:
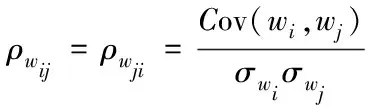
(15)
式中:ρwij为随机变量wi与wj之间的相关系数;Cov(wi,wj)为wi与wj的协方差;σwi,σwj为wi与wj的标准差。
根据三阶多项式正态变换(third-order p ̄o ̄l ̄y ̄n ̄o ̄m ̄ial normal transformation,TPNT)理论[14],具有相关性的随机变量空间W可由独立的服从标准正态分布随机变量空间Z的三阶多项式表示,即:

(16)
式中:ai(k)(k=0,1,2,3)为各项系数;zi为独立的服从标准正态分布的随机变量。
利用wi_st=(wi-μwi)/σwi将随机变量wi进行标准化,则有:

(17)
式中:bi(k)(k=0,1,2,3)为标准化后对应的各项系数。显然各项系数满足以下关系:
(18)
根据矩法原理,式(17)中等式两边的各阶原点矩相等,取前四阶原点矩的相等关系可展开得到4个方程:

(19)
式中:χ为wi_st的偏度;κ为wi_st的峰度。
通过求解式(19)非线性方程组可得bi(k),再根据式(18)求得ai(k),最后根据式(20)可计算得到具有相关性的服从标准正态分布的随机变量空间Y的相关系数矩阵中的各元素ρyij。
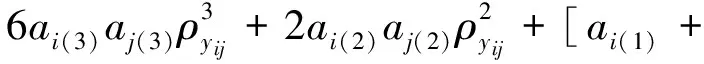
(20)
相关系数应为区间[-1,1]内一实数,同时在上述进行空间映射时,相关系数也应为同号,即ρyij须满足:
(21)
文中建立满足给定相关性水平的输入变量概率模型的步骤为:
(1) 产生满足独立正态分布的样本矩阵S,其维数为m×N,N为样本规模;
(2) 运用TPNT理论以及求解代数方程的方法求取具有相关性的标准正态分布随机变量Y的等效相关系数矩阵RY,即通过式(16—21)求取RY中的各元素ρyij;
(3) 根据式(22)对RY进行Cholesky分解[15]
RY=LYLYT
(22)
式中:LY即为Cholesky因式分解所得的下三角矩阵。
随后可由Y=LYS获得具有相关性的服从标准正态分布的样本矩阵Y;
(4) 通过等概率转换原则[15-16]得到满足相关性水平的样本矩阵W,即对每个样本利用式(23)由yi求取wi。
F(wi)=Φ(yi)
(23)
式中:F(wi)为wi的累积分布函数,Φ(yi)为yi的累积分布函数。
2.3 算法流程
文所提PLF计算的流程如下:
(1) 输入原始数据,包含微电网网架数据、电源和负荷的基本参数以及所对应的概率模型;
(2) 设定样本规模,对于相互独立的随机变量基于概率模型进行抽样;
(3) 对于相关的随机变量,由给定的F(W)及RW由式(14—23)建立满足给定相关性水平的样本矩阵;
(4) 将全部样本逐个进行孤岛微电网潮流计算,并保存频率及电压的计算结果;
(5) 对计算结果进行统计,求取频率及电压的的概率密度函数(probability density function,PDF)及累积分布函数(cumulative distribution function,CDF),两者满足以下关系:
(24)
式中:X为状态变量,即频率及节点电压;FX(x)为状态变量X的CDF;fX(x)为状态变量X的PDF。算法流程如图1所示。

图1 算法流程Fig.1 Algorithm flow chart
3 算例分析
以Benchmark 0.4 kV低压微电网[17]作为算例系统,如图2所示。其中S1打开,S2闭合,构成孤岛微电网系统。系统基准容量取100 kV·A,假定孤岛微电网的安全运行范围为fmax=1.004 p.u.,fmin=0.996 p.u.,Umax=1.05 p.u.,Umin=0.95 p.u.。

图2 Benchmark 0.4 kV低压微电网系统Fig.2 Benchmark 0.4 kv low-voltage microgrid system
接入设备参数见表1,其中节点13—17的电源中,PV及WT采取MPPT的控制方式,在单一样本潮流计算中视为恒功率电源,而其他的蓄电池组、微型燃气轮机等采取对等控制,共同参与微电网频率及电压的调节。考虑到负荷情况,在节点14及17进行必要的电容器固定补偿。

表1 算例中接入的设备及参数Tab. 1 Example of access to theequipment and parameters
负荷参数见表2。各节点恒阻抗、恒电流、恒功率负荷占比统一取为0.3,0.3,0.4,静态频率调节系数取kLpi=2,kLqi=-2[5]。负荷服从正态分布,负荷波动的标准差取为期望值的10%。

表2 负荷参数Tab. 2 Load parameters
各PV出力满足Beta分布,其中形状参数为α= 1.693,β=5.162。WT出力满足Weibull分布,切入风速2.7 m/s,额定风速6.7 m/s,可计算得a=-40.5,b=15,另外有形状参数k=2.94,尺度参数c=3.03。
场景1:假定节点15的WT退出运行,PV之间的相关系数ρPP取为0.8。
是否计及相关性的2种情况下所求得的频率及节点电压标准差对比如表3所示。

表3 场景1的状态变量的标准差对比Tab. 3 Standard deviation comparisonof state variables in scene 1
由表中数据可知,计及相关性后系统频率可能的波动范围明显增大,主要是节点15与节点16的PV出力呈现将强的相关性,将引起系统功率的较大幅度波动。若不计相关性的影响将会带来较大误差,频率的相对误差将近20%。
由于PV只输出有功功率,有功功率的平衡主要影响频率。对比节点15与节点16的PV出力相互独立以及计及相关性下的频率分布情况,频率的PDF及CDF如图3所示。

图3 场景1的频率PDF及CDFFig.3 Frequency PDF and CDF in scene 1
场景2:节点15的WT投入运行,PV之间的相关系数ρPP取为0.8,由于风光通常存在互补性,PV与WT之间的相关系数ρPW取为-0.6。
是否计及相关性的2种情况下所求得的频率及节点电压标准差对比如表4所示。

表4 场景2的状态变量的标准差对比Tab. 4 Standard deviation comparisonof state variables in scene 2
由表中数据可知,由于PV及WT出力成负相关性,即风光互补,提高了可再生能源输出的稳定性,与不考虑相关性的情况相比频率波动范围大大减小。若将风光出力视为相互独立则会产生极大的误差,由此可见本文计及DG出力相关性的计算结果更符合实际情况,能够更准确地评估频率及电压质量。
同样对比各DG出力相互独立以及计及相关性下的频率分布情况,频率的PDF及CDF如图4所示。
使用盒须图绘制出场景2下的节点电压分布情况,如图5所示。场景二下各节点电压都在一定范围内波动,均处于合格范围内,其中节点16波动区间较大,主要由于节点16的PV出力存在随机性,且容量较大。而节点15同样安装了PV但由于还有WT的存在,风光出力互补因此使得总体出力更为稳定,电压波动也较小些。

图4 场景2的频率PDF及CDFFig.4 Frequency PDF and CDF in scene 2
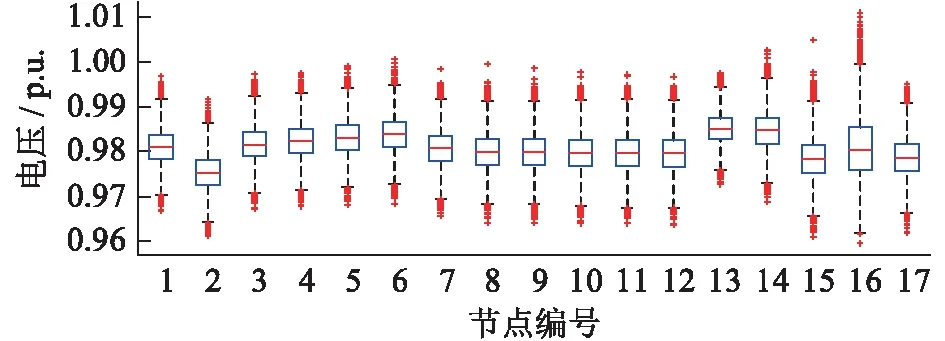
图5 节点电压盒须图Fig.5 Node voltage box plot
4 结论
文中提出一种计及DG出力相关性的孤岛微电网PLF计算方法,可用于求解对等控制模式下的孤岛微电网PLF。通过算例分析,获得以下结论:
(1) 孤岛微电网中的可再生能源主要是光伏及风力发电,由本文场景1的情况可以看出同类DG出力具有强相关性的情况下将加剧孤岛微电网的频率波动;
(2) 一般来说,风光出力存在天然的互补性,由本文场景2对比结果可知,通过风光互补能够获得较为稳定的出力,使得频率波动范围减小,可提高孤岛微电网运行的安全性;
(3) 文中计及DG出力相关性的PLF相比于相互独立的抽样模拟更符合实际情况,能够为孤岛微电网的运行提供可信的参考数据,存在应用价值。
参考文献:
[1] HATZIARGYRIOU N,ASAND H,IRAVANI R,et al. Microgrids [J]. IEEE Power and Energy Magazine,2007,5(4):78-94.
[2] KATIRAEI F,IRAVANI R,HATZIARGYRIOU N,et al. Microgrids management[J]. IEEE Power and Energy Magazine,2008,6(3):54-65.
[3] 彭寒梅,曹一家,黄小庆. 对等控制孤岛微电网的静态安全风险评估[J]. 中国电机工程学报,2016, 36(18):4837-4846.
PENG Hanmei,CAO Yijia,HUANG Xiaoqing. Static security risk assessment of islanded microgrids under peer-peer control[J]. Proceedings of the CSEE,2016,36(18):4837-4846.
[4] MUMTAZ F,SYED M H,HOSANI M A,et al. A novel approach to solve power flow for islanded microgrids using modified Newton Raphson with droop control of DG[J]. IEEE Transactions on Sustainable Energy,2015,6(12):1-11.
[5] 潘忠美,刘健,石梦,等. 计及电压/频率静特性的孤岛微电网电压稳定性与薄弱节点分析[J]. 电网技术,2017,41(7):2214-2221.
PAN Zhongmei,LIU Jian,SHI Meng,et al. Static voltage stability and weak bus analysis of islanded microgrids considering static voltage/frequency characteristics[J]. Power System Technolgy,2017,41(7):2214-2221.
[6] ABDELAZIZ M M,FARAG H E,EL-SAADANY E F,et al. A novel and generalized three-phase power flow algorithm for islanded microgrids using a newton trust region method[J]. IEEE Trans on Power Systems,2013,28(1):190-201.
[7] 彭寒梅,曹一家,黄小庆. 基于 BFGS 信赖域算法的孤岛微电网潮流计算[J]. 中国电机工程学报,2014,34(16):2629-2638.
PENG Hanmei,CAO Yijia,HUANG Xiaoqing. Power flow calculation of islanded microgrids based on BFGS trust region method[J]. Proceedings of the CSEE,2014,34(16):2629-2638.
[8] 李培帅,施烨,吴在军,等. 孤岛微电网潮流的类奔德斯分解算法[J]. 电力系统自动化,2017,41(14):119-125.
LI Peishuai,SHI Ye,WU Zaijun,et al. Power flow calculation method similar to benders decomposition for islanded microgrid[J]. Automation of Electric Power Systems,2017,41(14):119-125.
[9] 金楚,黎嘉明,徐沈智,等. 大规模光伏发电并网概率潮流计算及对电网的影响[J]. 电力工程技术,2017,36(1):1-8.
JIN Chu,LI Jiaming,XU Shenzhi,et al. Probabilistic load flow calculation and influence analysis for power grid connected with large scale photovoltaic generation system[J]. Electric Power Engineering Technology,2017,36(1):1-8.
[10] 卫鹏,刘建坤,周前,等. 基于半不变量和Gram-Charlier级数展开法的随机潮流算法[J]. 电力工程技术,2017,36(1):34-38.
WEI Peng,LIU Jiankun,ZHOU Qian,et al. A probabilistic power flow algorithm based on semi-variable and gram-charlier series expansion[J]. Electric Power Engineering Technology,2017,36(1):34-38.
[11] 丁明,李生虎,黄凯. 基于蒙特卡罗模拟的概率潮流计算[J]. 电网技术,2001,25(11):10-14, 22.
DING Ming,LI Shenghu,HUANG Kai. Probabilistic load flow analysis based on monte-carlo simulation[J]. Power System Technology,2001,25(11):10-14, 22.
[12] 段玉兵,龚宇雷,谭兴国,等. 基于蒙特卡罗模拟的微电网随机潮流计算方法[J]. 电工技术学报,2011,26(S1):274-278.
DUAN Yubing,GONG Yulei,TAN Xinguog,et al. Probabilistic power flow calculation in microgrid based on monte-carlo simulation. Transactions of China Electrotechnical Society[J].2011,26(S1):274-278.
[13] 刘明波,简淦杨,董萍. 孤岛微电网的随机潮流计算[J]. 华南理工大学学报(自然科学版),2014,42(4):13-18.
LIU Mingbo,JIAN Ganyang,DONG Ping. Stochastic power flow calculation of islanded microgrids[J]. Journal of South China University of Technology(Natural Science Edition),2014,42(4):13-18.
[14] 刘小团,赵晋泉,罗卫华,等. 基于TPNT和半不变量法的考虑输入量相关性概率潮流算法[J]. 电力系统保护与控制,2013,41(22):13-18.
LIU Xiaotuan,ZHAO Jinquan,LUO Weihua,et al. A TPNT and cumulants based probabilistic load flow approach considering the correlation variables[J]. Power System Protection and Control,2013,41(22):13-18.
[15] 石东源,蔡德福,陈金富,等. 计及输入变量相关性的半不变量法概率潮流计算[J]. 中国电机工程学报,2012,32(28):104-113.
SHI Dongyuan,CAI Defu,CHEN Jinfu,et al. Probabilistic load flow calculation based on cumulant method considering correlation between input variables[J]. Proceedings of the Chinese Society for Electrical Engineering,2012,32(28):104-113.
[16] 吴巍,汪可友,李国杰. 计及光伏发电相关性的多重积分法概率潮流计算[J]. 中国电机工程学报,2015, 35(3):568-575.
WU Wei,WANG Keyou,LI Guojie. Probabilistic load flow calculation method based on multiple integral method considering correlation of photovoltaic generation[J]. Proceedings of the CSEE,2015,35(3):568-575.
[17] 贾宏杰,戚艳,穆云飞. 基于家居型温控负荷的孤立微电网频率控制方法[J]. 中国科学:技术科学,2013,56(3):693-702.
JIA HongJie,QI Yan,MU YunFei. Frequency response of autonomous microgrid based on family-friendly controllable loads[J]. Science China:Technological Sciences,2013,56(3):693-702.

