含分布式储能的配电网多目标运行优化策略研究

吴　霜， 季　聪， 孙国强

(1． 国网江苏省电力有限公司经济技术研究院，江苏 南京 210008；2． 江苏方天电力技术有限公司，江苏 南京 211102；3． 可再生能源发电技术教育部工程研究中心(河海大学)，江苏 南京 210098)

0　引言

随着人民生活水平不断提高，家庭电器保有率持续提升，在冬夏两季，尤其春节期间，配电网负荷峰谷差不断扩大，各地配变，尤其是农网配变重载、过载情况时有发生[1]。配电网的增容改造面临着征地困难、投资成本高等问题，而储能设备容量的不断扩大、投资成本不断降低[2-3]，为配电网削峰填谷和优化运行提供了一种新的思路[4-5]。目前，相关领域的专家和学者也已经开展了大量的研究工作，取得了很好的研究成果[7]，国内外也有不少成功的应用案例和示范工程[8-9]。

文献[10—14]采用动态规划法、锥优化法、松弛法及混合法求解了含规模化储能设备电力系统的运行策略优化，并取得了很好的优化效果，但由于含储能的电力系统运行优化模型涉及的变量多、时段多，且变量之间存在复杂的耦合关系，导致约束条件复杂、计算量大，给模型的求解带来了较大的难度，相应的公式推导、代码开发都非常复杂。如何有效处理多时段耦合关系，提高求解效率是一个复杂的难题。自动微分技术(automatic d￣i￣f￣f￣e￣r￣e￣n￣tial, AD)通过链式法则自动完成微分操作，可以实现梯度类算法(例如牛顿法、内点法、序列二次规划法等)中雅克比矩阵、海森矩阵的自动生成，有效地减少了公式推导、代码开发的工作量，而且AD技术目前已在电力系统潮流计算[15]、状态估计[16]和最优潮流[17-18]中得到了广泛的应用。

因此，在分析分布式储能设备的充放电模型和建立含储能电力系统的多时段优化运行模型的基础上，引入稀疏AD技术，在尽量不增加计算时间的基础上，减少公式推导和代码编写的工作量。另外，考虑到储能电量约束复杂而导致AD求导工作量过大的问题，采用储能电量约束约简方法，降低了模型的复杂度，并通过某实际配电网储能示范工程的算例仿真，验证了文中模型的准确性、算法的高效性与策略的可行性。

1　储能的充放电模型

储能设备连接到配电网以后，在充电时，可以将其视为负荷，而放电时视作分布式电源。

在t时刻，当储能充电时，t时刻末储能电量为：

(1)

式中：下标i为储能设备的编号，取值范围为1,2,…，n。

而当储能放电时，t时刻末储能电量为：

(2)

t时刻与t-1时刻的储能电量存在如式(1)、(2)所示的耦合关系，这种耦合关系在程序实现时比较困难，通常会将式(1)、(2)推广为如下公式：

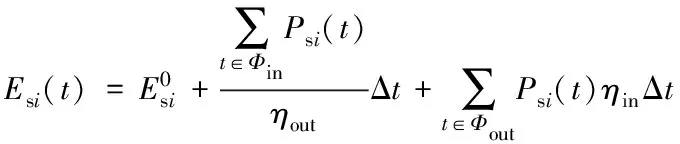
(3)

2　含储能电力系统的多时段优化运行模型

2.1　目标函数

2.1.1最小电量损耗

(4)

式中：T为运行时间的时段数；Nbr为支路数；gk(i,j)为第k条支路(首末节点分别为i，j)支路电导；Vi(t)，Vj(t)和θi(t)，θj(t)分别为节点i，j在t时段的节点电压幅值和相角，θij(t)=θi(t)-θj(t)。

由于储能充放电过程中有损耗，因此该目标只有在储能设备充放电损耗低于线路传输损耗时，储能才会发生充放电行为。

2.1.2最小负荷波动

在数学上，方差可以反映随机变量偏离其均值的程度，负荷的方差可以反映负荷曲线的波动程度，文中选取储能设备补偿后的电网负荷曲线的方差作为目标函数：

(5)

式中：N为配电网的节点数；Ns为储能设备个数；Pdi(t)为第i个节点的在时段t的负荷；Psj(t)为第j个储能设备在时段t的充、放电功率；Pav为T个时段内整个配电网的平均负荷，其计算公式如下：

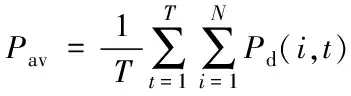
(6)

2.1.3多目标优化

多目标优化对电量损耗和负荷波动综合考虑，其目标函数如下所示：

(7)

2.2　等式约束

2.2.1普通节点功率平衡方程

(8)

2.2.2连有储能设备的节点功率平衡方程

(9)

2.2.3储能设备的电量平衡方程

储能设备的电量平衡方程由式(1)和(2)组成。

2.3　不等式约束

不等式约束包含静态约束和动态约束两种，其中静态约束为节点电压上下限约束和储能充放电功率上下限约束，动态约束为储能电量约束。

2.3.1节点电压约束

(10)

2.3.2储能充放电功率约束。

(11)

2.3.3储能电量约束

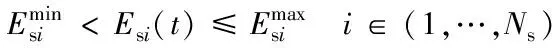
(12)

3　求解方法

3.1　求解思路

含储能系统的策略优化模型求解思路基本如图1所示。

图1　优化模型的求解思路Fig.1　Solution of optimization model

(1) 根据配电网历史负荷数据开展配电网日前负荷预测，根据事先确定好策略选定储能设备充放电时段；

(2) 以日前负荷预测、配电网网络拓扑、储能设备初始电量及储能设备充放电时段为输入，建立含储能系统的策略优化模型；

(3) 开展配电网多点储能设备多时段优化，得到各时段储能设备的全局最优充放电策略。

在多时段优化算法的选择上，文中选取内点优化器(interior point optimizer，IPOPT)进行求解。IPOPT以原-对偶内点法为核心求解非线性凸规划问题，在优化领域得到了高度的认可和广泛的应用[19-20]。

3.2　充放电时段选择

1.1中提到，在进行多时段充放电策略联合优化之前，储能设备的充放电时段应已确定。但储能设备充放电时段的选择，将直接影响配电网的运行效率和储能设备投资者的经济收益，而且储能设备的寿命与充放电次数有直接关系，因此应对充放电次数加以限制。目前储能充放电时段的选择有以下2种。

(1) 模式1：根据分时电价确定充放电时段。与1.2中的低充高放对应，如图2所示，在峰电价时段(8:00 am—21:00 pm)放电，谷电价时段(21:00 pm—8:00 am)充电，这种充电模式可以保证储能设备投资者赚取的电价差利润最大化。

图2　根据分时电价确定充放电时段Fig.2　Determining charging/discharging time periods based on time-of-use price

(2) 模式2：根据负荷情况确定充放电时段。根据负荷预测得到待优化时段的平均负荷，当预测负荷高于平均负荷时储能放电，当预测负荷低于平均负荷时储能充电，如图3所示。

图3　根据负荷情况确定充放电时段Fig.3　Determining charging/discharging time periods based on power load level

第二种充放电时段选择存在储能充放电次数过多的风险，因此也需要事先对预测负荷曲线加以分析，以避免上述情况的发生。目前较为典型的负荷曲线为全天型、单峰型、双峰型和夜间型，这4种类型的负荷曲线均不会发生储能充放电次数过多的现象，因此第二种充放电时段选择在绝大多数情况下是可行的。

3.3　求解效率提升

(1) 自动微分技术应用。对于多时段耦合优化问题，内点法求解过程中所需的雅可比矩阵计算和海森矩阵计算编码工作量巨大，但IPOPT并不提供上述计算功能，需要开发人员自行编码。基于C++重载的自动微分(automatic differentiation by over-loading in C++，ADOL-C)，是一种自动微分工具，可以为IPOPT的求解过程提供雅可比矩阵计算和海森矩阵计算功能，而且它提供了稀疏求导功能，尽可能地缩短了自动求导所需的时间[21]。

(2) 储能电量约束缩减。由于储能设备在t时刻的存储电量与之前的0～t-1个时段均有关联，因此公式(10)的自动微分和矩阵运算的计算量很大。考虑到3.2提到的2种充电方式，储能设备在整个优化时间区间内充放电状态转换次数不多，且在某一充电时间区间内，只需要对最后一个充电时段加以约束即可(该策略对放电状态同样适用)。因此，在整个优化时间区间内，只需要找到储能充放电状态切换的时刻，并对这几个时刻进行电量约束，即可实现整个优化时间区间内的储能电量约束。例如图2储能电量约束由96个缩减为3个，图3储能电量约束由96个缩减为5个。

4　算例分析

为验证文中所述模型与策略的可行性和准确性，以某19节点实际配电网为例，进行算例分析。

4.1　算例基本参数

该实际配电网拓扑结构如图4所示，储能设备参数如表1所示。

图4　某实际配电网拓扑结构Fig.4　Topology of a practical distribution network

表1　储能设备参数Tab.1　Parameters of energy storage

110 kV变压器电压约束范围为[0.95, 1.1]，其余节点电压运行区间为[0.95, 1.05]；各储能设备初始电量Es0=Esmax×20%，运行区间为[Esmax×20%,Esmax]。

4.2　多目标优化结果比较

以4.1述及的配电网某典型日负荷为例，储能充放电模式选择模式2，进行储能充放电策略优化，优化前后的典型日负荷曲线如图5所示，优化前后的系统电量损耗和负荷波动如表2所示。

图5　储能平抑后的负荷曲线Fig.5　Load curve with or without energy storage

表2不同目标函数下的系统运行指标
Tab.2Operation index of the distribution network with different object functions

参数无储能最小损耗最小波动多目标电量损耗/(kW·h)6501．466466．646700．966470．29负荷波动/kW29．66×1065．33×1061．94×1063．28×106

可以得出如下结论：

(1) 以最小电量损耗为目标函数时，系统电量损耗下降了34.82 kW·h，波动率也下降了44.8%；

(2) 以最小负荷波动为目标函数时，系统波动率虽然下降了79.92，但电量损耗增加了199.50 kW·h；

(3) 多目标优化时(α=0.5)，系统电量损耗下降了31.17 kW·h，负荷波动率下降了66.05%。

因此可见，多目标优化综合考虑了系统电量损耗和负荷波动，在牺牲很少量电量损耗的前提下获得了很好的削峰填谷效果。

3种目标函数下，储能总体运行参数如图6所示。

图6　储能总体功率和电量曲线Fig.6　Total power and electricity curves of energy storage

由图6可见：

(1) 以最小负荷波动为目标函数时，储能设备的充放电功率和电量均最高，而储能的充放电过程加剧了系统的电量损耗，印证了表2的结论。

(2) 储能设备在充电过程中，存储电量达到了容量上限，若系统配变的储能容量足够大，系统的负荷曲线将被平抑成一条平稳的直线。

4.3　充放电模式比较

以图2的负荷曲线为例，储能设备选择不同的充放电模式，以多目标优化为目标函数(α=0.5)，进行储能充放电策略优化，优化前后的负荷曲线如图7所示。

图7　2种模式下的负荷曲线Fig.7　Load curve in two different modes

可见，2种模式下，负荷曲线均得到一定程度的平抑，但2条平抑曲线略有差别：模式2的负荷曲线整体更加平稳，而模式1在21:00负荷曲线会有一个上升，主要由于储能受分时电价的影响，此时不再放电。

2种运行模式下，储能总体运行参数如图8所示。

图8　不同模式下储能总体功率和电量曲线Fig.8　Total power and electricity curves of energy storage in two different modes

由图8可以看出，由于充放电时段设置的差异，储能的充放电功率和存储电量有所差异，对2种模式下的储能充放电量进行统计，得出充放电电量时刻表，如图9所示。

图9　不同模式下储能充放电量统计Fig.9　Charging and discharging electricity of energy storage in two different modes

模式2由于储能在中午负荷下降时进行了充电，因此在8:00—11:30和18:00—21:30的负荷高峰有更多的放电量，使负荷曲线更加平稳。

2种模式的电量损耗和负荷波动如表3所示。其中峰谷的电价按照峰0.55 元/(kW·h)，谷0.35 元/(kW·h)执行。

表3　不同模式下的系统运行指标Tab.3　Operation index of the distributionnetwork in different modes

由表3可得出如下结论：

(1) 以最小电量损耗为目标函数时，模式1的电量损耗和负荷波动均高于模式2，主要是由于在中午的负荷降落时段和晚上21:00—22:00的负荷高峰，模式1并未启动储能进行负荷曲线平抑；

(2) 以最小负荷波动为目标函数时，模式1的负荷波动明显高于模式2，发生此现象的原因与(1)相同，但由于模式2时储能的充放电量较模式1更大，导致系统的电量损耗增加；

(3) 采取多目标优化策略后，模式1、模式2的电量损耗和负荷波动均得到了较大程度的优化，2种模式下的运行参数均较为理想；

(4) 虽然从系统的运行参数看，模式2基本上要优于模式1，但实际而言，无论是哪种目标函数，模式1的运行利润均高于模式2(即使是以最小负荷波动为目标函数时系统运行发生亏损，模式1的亏损也要远远低于模式2)。

5　结语

随着配电网负荷峰谷差的不断扩大，配变重过载问题时有发生，配电网面临着越来越大的运行风险和运营压力，而储能设备在配电网中的应用，可以有效降低配电网负荷峰谷差异和重过载风险。文中利用稀疏自动微分技术减少代码编写工作量、通过储能电量约束约简降低模型复杂度的方式，极大地方便了模型的求解，提升了计算效率，通过某实际配电网储能示范工程的算例仿真，验证了模型的准确性、算法的高效性与策略的可行性。

参考文献：

[1] 贺建章，王海波，季知祥，等． 面向智能电网的配电变压器重过载影响因素分析[J]． 电网技术，2017，41(1)：279-284.

HE Jianzhang，WANG Haibo，JI Zhixiang，et al． Analysis of factors affecting distribution transformer overload in smart grid[J]． Power System Technology，2017，41(1)：279-284.

[2] 薛金花，叶季蕾，陶琼，等． 采用全寿命周期成本模型的用户侧电池储能经济可行性研究[J]． 电网技术，2016，40(8)：2471-2476.

XUE Jinhua，YE Jilei，TAO Qiong，et al． Economic feasibility of user-side battery energy storage based on whole-life-cycle cost model[J]． Power System Technology，2016，40(8)：2471-2476.

[3] 田崇翼，张承慧，李珂，等． 含压缩空气储能的微网复合储能技术及其成本分析[J]． 电力系统自动化，2015，39(10)：36-41.

TIAN Chongyi，ZHANG Chenghui，LI Ke，et al． Composite energy storage technology with compressed air energy storage in microgrid and its cost analysis[J]． Automation of Electric Power System，2015，39(10)：36-41.

[4] 石磊，伍阳，刘皓明，等． 独立运行微电网平抑有功差额波动研究[J]． 江苏电机工程，2012，31(3)：1-4，8.

SHI Lei，WU Yang，LIU Haoming，et al． Research on active power difference balancing of autonomous operation microgrid[J]． Jiangsu Electrical Engineering，2012，31(3)：1-4，8.

[5] 杨玉青，牛利勇，田立亭，等． 考虑负荷优化控制的区域配电网储能配置[J]． 电网技术，2015，39(4)：1019-1025.

YANG Yuqing，NIU Liyong，Tian Liting，et al． Configuration of energy storage devices in regional distribution network considering optimal load control[J]． Power System Technology，2015，39(4)：1019-1025.

[6] 王钤，徐备，张师. 分布式储能对配电网电压稳定的影响分析[J]. 广东电力，2017，30(5)，48-51.

WANG Qian, XU Bei, ZHANG Shi, et al. Analysis on influence of distributed energy storage on voltage stability of power distribution network[J]. Guangdong Electric Power，2017，30(5)：48-51.

[7] 王承民，孙伟卿，衣涛，等． 智能电网中储能技术应用规划及其效益评估方法综述[J]． 中国电机工程学报，2013，33(7)：33-41，5.

WANG Chengmin，SUN Weiqing，YI Tao，et al． Review on energy storage application planning and benefit evaluation methods in smart grid[J]． Proceedings of the CSEE，2013，33(7)：33-41，5.

[8] 胡娟，杨水丽，侯朝勇，等． 规模化储能技术典型示范应用的现状分析与启示[J]． 电网技术，2015，39(4)：879-885.

HU Juan，YANG Shuili，HOU Chaoyong，et al． Present condition analysis on typical demonstration application of large-scale energy storage technology and its enlightenment[J]． Power System Technology，2015，39(4)：879-885.

[9] 张翼． 电力储能技术发展和应用[J]． 江苏电机工程，2012，31(4)：81-84.

ZHANG Yi． The development and application of energy storage technology[J]． Jiangsu Electrical Engineering，2012，31(4)：81-84.

[10] 鲍冠南，陆超，袁志昌，等． 基于动态规划的电池储能系统削峰填谷实时优化[J]． 电力系统自动化，2012，36(12)：11-16.

BAO Guannan，LU Chao，YUAN Zhichang，et al． Load shift real-time optimization strategy of battery energy storage system based on dynamic programming[J]．Automation of Electric Power Systems，2012，36(12)：11-16.

[11] 赵金利，于莹莹，李鹏，等． 基于锥优化的储能系统参与配电网运行调节快速计算方法[J]． 电力系统自动化，2016，40(2)：30-35，48.

ZHAO Jinli，YU Yingying，LI Peng，et al． A fast calculation method of energy storage system for distribution network regulation based on conic programming[J]． Automation of Electric Power Systems，2016，40(2)：30-35，48.

[12] DENNICE GAYME，UFUK TOPCU． Optimal power flow with large-scale storage integration[J]． IEEE Transactions on Power Systems，2013，28(2)：709-717.

[13] 张惠生，赵兴勇，王凯武，等. 基于风光互补微电网的复合储能控制策略[J]. 广东电力，2017，30(2)：48-53,96.

ZHANG Huisheng, ZHAO Xingyong, WANG Kaiwu,et al. Control strategy for hybrid energy storage based on wind/photovoltaic complementary micro-grid system[J]. Guangdong El-ectric Power，2017，30(2)：48-53+96.

[14] 向育鹏，卫志农，孙国强，等． 基于全寿命周期成本的配电网蓄电池储能系统的优化配置[J]． 电网技术，2015，39(1)：264-270.

XIANG Yupeng，WEI Zhinong，SUN Guoqiang，et al． Life cycle cost based optimal configuration of battery energy storage system in distribution network[J]． Power System Technology，2015，39(1)：264-270.

[15] 季聪，卫志农，孙国强，等． 基于自动微分技术的VSC-HVDC潮流计算[J]． 电力系统及其自动化学报，2013，25(2)：1-6.

JI Cong，WEI Zhinong，SUN Guoqiang，et al． Power flow calculation of the AC-DC system with VSC-HVDC based on automatic differentiation[J]． Proceedings of the CSU-EPSA，2013，25(2)：1-6.

[16] 叶芳，卫志农，孙国强，等． 基于自动微分技术的电力系统状态估计算法[J]． 电力系统保护与控制，2010，38(17)：91-95，100.

YE Fang，WEI Zhinong，SUN Guoqiang，et al． State estimation of power systems with automatic differentiation technology[J]． Power System Protection and Control，2010，38(17)：91-95，100.

[17] 耿光超，江全元． 基于自动微分技术的内点法最优潮流算法[J]． 电力系统自动化，2008，32(23)：41-45.

GENG Guangchao，JIANG Quanyuan． An automatic differentiation based interior-point method for optimal power Flow[J]． Automation of Electric Power Systems，2008，32(23)：41-45.

[18] 季聪，卫志农，汤涌，等． 基于自动微分技术的VSC-HVDC内点法最优潮流[J]． 电网技术，2012，36(10)：184-189.

JI Cong，WEI Zhinong，TANG Yong，et al． A primal-dual interior point method-based algorithm adopting automatic differentiation for optimal power flow of AC/DC power grid containing VSC-HVDC system[J]． Power System Technology，2012，36(10)：184-189.

[19] BK KAWAJIRI，CD LAIRD． Introduction to IPOPT: a tutorial for downloading, installing and usring IPOPT[Z]．2015，44-46.

[20] 李斌. 用电大数据的应用研究[J]. 电力需求侧管理,2016,18(4):41-45，55.

LI Bin. Application and research of electricity big data[J]. Power Demand Side Mangment, 2016,18(4):41-45，55.

[21] BA GRIEWANK． A package for the automatic differentiation of algorithms written in C/C++[Z]．2009，23-25.