基于点估计法的杆塔结构平均可靠度分析

黄　兴， 田　雷， 杨　洋，廖邢军， 蒲　凡， 李　钟

(1． 西南电力设计院有限公司，四川 成都 610021；2． 国网北京经济技术研究院，北京 102209)

0　引言

由于不可避免的随机性，可靠度成为结构设计的基础，实用设计表达式则是可靠度在结构设计中最直接的体现。然而，对输电塔杆塔结构而言，其可靠度与规范的目标可靠指标并不一定相同，究其根源，主要原因在于：目前输电塔结构设计规范基本上是参照建筑结构规范进行编制的[1]，而建筑结构规范中所涵盖的设计对象大多针对荷载效应比不大于3的情况[2]。然而，对于输电塔结构，其杆塔的自重较轻，承受的活荷载较高，导致其荷载效应比往往高于一般结构构件。当荷载效应比较高时，按照实用设计表达式设计出的构件可靠度水平则会降低。为研究输电塔杆塔构件荷载效应比对其可靠度水准的影响，许多专家学者对现有输电塔规范的可靠度水平进行了校准。冯云芬等[3]考虑恒荷载与风荷载的简单组合，研究了风荷载效应比变化范围为0.1～100时可靠度水准的变化；李峰等[4]研究了风荷载效应比为4.0～8.0的可靠度水准平均值；王松涛[5]则计算了风荷载效应比范围为4.0～10.0的可靠度指标平均值；刘静波[6]研究了风荷载效应比1.0～40.0范围内可靠度指标的变化，并得到可靠度指标的平均值。可以看出，现有研究的一般做法为：先假定荷载效应比的取值范围，再在该范围内选取多个离散的荷载效应比值，计算这些离散点处的可靠度指标，并计算这些可靠度指标的平均值。然而，荷载效应比范围的设定以及离散点的选取过于主观，得到的可靠指标平均值不具有统计意义。因此，如何全面客观地考虑荷载效应比的取值，是研究荷载效应比对可靠度水准影响的关键。

为此，文中首次尝试将荷载效应比视为随机变量，沿用点估计法的基本思想，以荷载效应比的分布为输入，得到基于荷载效应比分布的、具有统计意义的杆塔结构加权平均可靠度指标。

1　荷载效应比分布拟合

1.1　样本点选取

不失一般性，文中选取恒荷载+风荷载简单组合(下称恒风组合)下的轴心受压杆件为例，其它荷载组合下不同受力方式杆件的分析可依次类推。轴心受压杆件的风荷载效应比ρW的计算公式为：

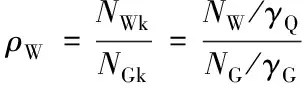
(1)

式中：NWk为风荷载引起的杆件轴心压力标准值;NGk为恒荷载引起的杆件轴心压力标准值;NW为风荷载引起的杆件轴心压力设计值;NG为恒荷载引起的杆件轴心压力设计值;γQ为活荷载分项系数;γG为恒载分项系数。

文中选取安徽到上海某条实际输电线路工程，并统计如表1所示8个不同工况下的直线塔的风荷载效应比。实际杆塔设计中，部分按照构造要求设计的辅材和按照统材要求设计的杆件不由设计表达式控制。综上所述，文中基于道亨软件，仅选取应力百分比大于50%的杆件作为风荷载效应比的有效样本进行统计分析，样本点共计1253个。

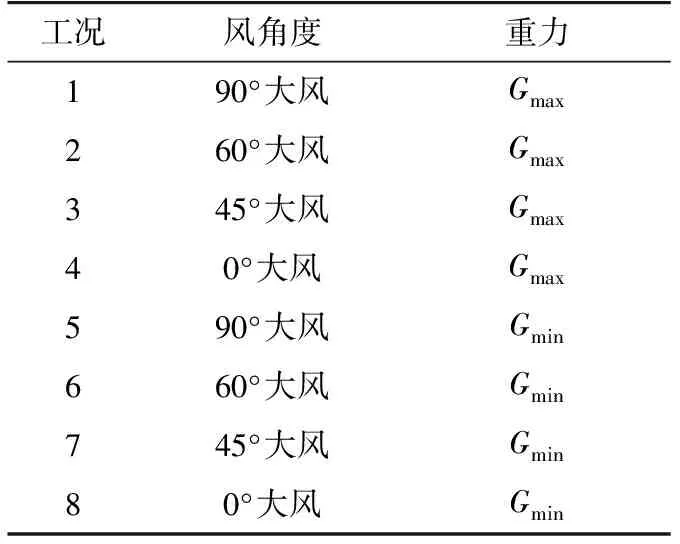
表1　工况选取Tab.1　Working conditions selected

其中，大风代表施加风速为30 m/s的风荷载；Gmax为重力荷载不利工况；Gmin为重力荷载有利工况。

1.2　分布拟合

基于以上样本，进而对样本的总体分布进行拟合。文中采用MATLAB软件的分布拟合工具箱近似得到总体分布密度函数曲线[7- 9]，共选取7种不同分布类型进行拟合，选用分布类型如表2所示。

表2　选用分布及简称Tab.2　Distributions used andthe corresponding abbreviations

根据上述7种分布类型进行分布拟合，可以得到如图1所示的概率密度函数的拟合，以及如图2所示的累计分布函数的拟合。

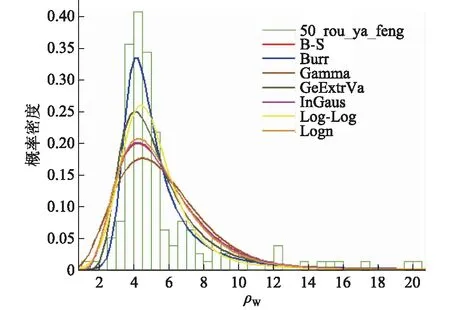
图1　风荷载效应比的概率密度函数Fig.1　PDF of wind load effect ratio

图2　风荷载效应比的累计分布函数Fig.2　CDF of wind load effect ratio

通过对比7种不同的分布，文中选取其中拟合程度较好的Log_Logistic分布，对应的均值和标准差分别为5.556 2和4.659 9。

2　基于点估计法的可靠度指标均值

2.1　功能函数的建立

DL/T 5154—2012架空送电线路杆塔结构设计技术规定[10]关于铁塔结构承载能力极限状态的设计表达式，是根据GB 50068—2001建筑结构可靠度设计统一标准的有关原则确定的。在结构可靠度分析中，结构的极限状态可由其功能函数来表达，功能函数形式为[11]：

Z=g(X1,X2,…,Xn)

(2)

式中：X=[X1，X2，...，Xn]为工程结构中存在的各种不确定信息的随机变量。从性质上来说，可以分为结构参数和荷载参数2类：第一类是结构抗力，用R表示；另一类是荷载的作用或作用效应，用S表示。当仅以荷载效应S、结构构件抗力R作为2个基本随机变量时，功能函数可表示为：

Z=g(R,S)=R-S

(3)

当Z<0时，结构处于失效状态；当Z>0时，结构处于可靠状态；当Z=0时，结构处于极限状态。

文中仅选取恒风组合下杆塔结构中轴心受压构件进行可靠度校准，其对应的功能函数为[12]：

Z=R-SG-SW

(4)

式中：R，SG，SW分别为输电塔杆塔构件的抗力随机变量、恒载随机变量和风荷载随机变量。

为计算式(4)的可靠度，需要得到上述随机变量的统计参数和分布类型。其中，值得注意的是，随机变量的均值由变量标准值乘以均值系数得到。

不失一般性，假设SGk=1，SWk=ρW[12]。对于杆塔结构的实用设计表达式，李峰等[7]在规范基础上考虑了导线线条风荷载调整系数和不同重现期基本风压换算系数的影响；王松涛等[5]进一步考虑了最小设计风速影响系数的影响。然而，已有研究并未考虑档距利用率和截面利用率的影响。因此，文中所采用的实用设计表达式在已有研究的基础上进一步引入了档距利用率和截面利用率，抗力标准值Rk如下式所示：

Rk=γ0γRγA{γG(SGk)+
γQ[βv((1-χ)SQk+βcχSQk/γ档距)]}

(5)

式中：γ0为结构重要性系数；γ档距为档距利用率，根据实际经验取1/0.9；γR为抗力分项系数；γA为截面利用率，根据实际经验取1/0.95；γG为恒载分项系数；γQ为可变荷载分项系数；SGk为永久荷载标准值；SQk为风荷载标准值；Rk为结构构件的抗力标准值；βv为最小设计风速影响系数，βc为导地线风荷载调整系数，βv和βc的取值见表3；χ为线条风荷载效应占风荷载总效应的比值，根据相关文献[3-5]和工程经验，取值范围为0.2～0.4。

表3　最小设计风速影响系数βv及导地线风荷载调整系数βcTab.3　Value of βv and βc

将SGk=1，SWk=ρW代入式(15)中，可进一步得到：

RK=γRγ0γA{γG+aρW}F(ρW)

(6)

式中：a=γQ{βv[(1-χ)+βcχ/γ档距]}。

综上所述，式(4)中随机变量的分布参数和分布类型如表4所示[5]。

表4　基本随机变量的统计信息Tab.4　Statistical information of basic variables

2.2　基于点估计法的平均可靠指标计算

通过上述分析可知，基本随机变量的统计参数是荷载效应比ρW的函数，当荷载效应比ρW确定时，即可利用JC[11]法求解式(4)的可靠指标β。因此，可靠指标β可以表达为荷载效应比ρW的隐式函数，如式(7)所示:

β=f(ρW)

(7)

式中：f(．)表示β与ρW的关系，为隐式函数。对于任一给定的ρW，β可方便地由JC法确定[13]。进而，可靠度指标的均值可表示为:

(8)

式中：Ωρ为ρ的取值域；p(．)表示概率密度函数。

沿用点估计法的基本思想[14-18]，对上式采用一维Gauss-Hermite数值积分，可靠度指标的均值即平均可靠指标可由式(9)表示：

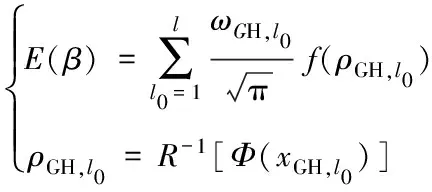
(9)

式中：ωGH，i是Gauss-Hermite积分的权系数；xGH，i是根据Gauss-Hermite积分的节点；Φ(．)表示标准正态分布的分布函数；R-1(．)表示Rosenblatt逆变换函数[19]；ρGH，i是根据xGH，i的Rosenblatt逆变换得到的对应荷载效应比的值；l为积分点总数，文中取l=7，Gauss-Hermite 7点积分的权系数与节点示于表5。

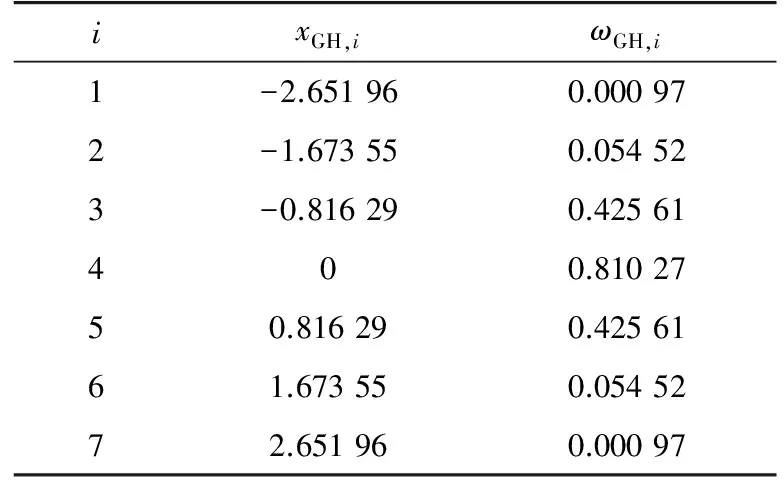
表5　Gauss-Hermite 7点积分的权系数与节点Tab.5　Abscissas and weights forGauss-Hermite quadrature with l=7

3　风荷载下输电塔可靠度的校准

基于以上平均可靠指标的计算方法，分别讨论在不同风速下(22 m/s，24 m/s，26 m/s，27 m/s，29 m/s，30 m/s，32 m/s，34 m/s，35m/s)，不同线条风占比(χ=0.2，0.3，0.4)和不同的结构重要性系数(γ0=1.0，1.1，1.2)对平均可靠指标的影响，可靠度校准结果如表6—11所示。

综合上述，根据表6—11所示平均可靠度指标，可进一步求得当γ0=1时，可靠指标的均值为3.38；γ0=1.1时，可靠指标的均值为3.76；γ0=1.2时，可靠指标的均值为4.11；而基于此分布模型下采用规范规定的使用设计表达式计算可知，当γ0=1时，可靠指标的均值为2.77；γ0=1.1时，可靠指标的均值为3.28；γ0=1.2时，可靠指标的均值为3.75。

表6　风速22 m/s时平均可靠指标Tab.6　Mean value of β at v=22 m/s

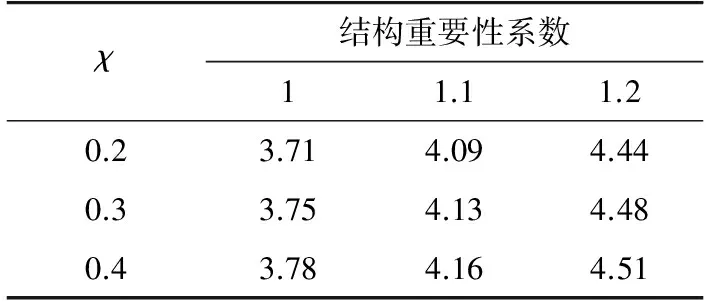
表7　风速24 m/s时平均可靠指标Tab.7　Mean value of β at v=24 m/s

表8　风速26 m/s时平均可靠指标Tab.8　Mean value of β at v=26 m/s

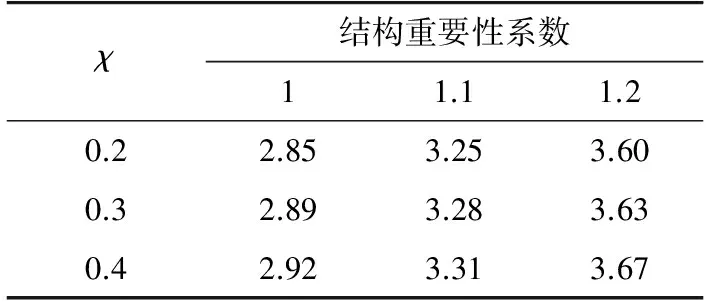
表9　风速27 m/s时平均可靠指标Tab.9　Mean value of β at v=27 m/s

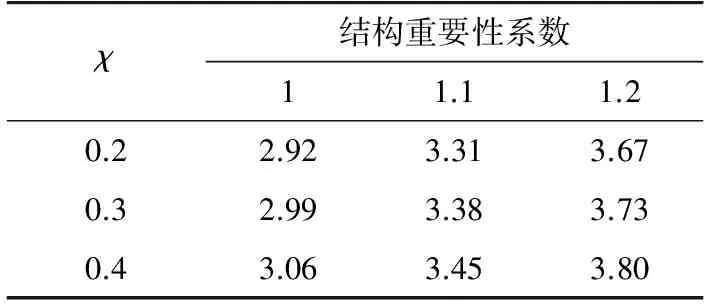
表10　风速30 m/s时平均可靠指标Tab.10　Mean value of β at v=30 m/s

表11　风速35 m/s时可靠指标Tab.11　Mean value of β at v=35m/s

4　结语

基于荷载效应比的分布拟合，并结合点估计法的基本思想，文中提出了输电塔杆塔结构构件平均可靠度指标的计算方法。与传统方法相比，文中方法首次尝试利用荷载效应比的分布校验现有规范内蕴的平均可靠水准。为验证方法的可行性，以输电塔恒风组合的轴心受压构件为研究对象，首先通过大量结构分析得到荷载效应比的样本点，再通过分布拟合得到荷载效应比的分布。基于该分布，分别计算了不同风速下，不同线条风占比以及不同结构重要性系数下的输电塔平均可靠指标。

参考文献：

[1] GB/50068—2001 建筑结构可靠度设计统一标准[S].中国建筑工业出版社，2002.

GB/50068—2001 Unified standard for reliability design of building structures [S]. China Buolding Industry Press,2002.

[2] 蒋友宝，杨伟军． 可变荷载效应占高比重时荷载分项系数取值研究[J]． 建筑结构学报，2012，33(12)：130-135.

JIANG Youbao，YANG Weijun．Research on values of load partial factors with large ratios of variable load effects[J]．Journal of Building Structures，2012，33(12)：130-135.

[3] 冯云芬，贡金鑫． 输电线路杆塔构件可靠度校准[J]． 电力建设，2014，35(5)：13-20.

FENG Yunfen，GONG Jinxin． Reliability calibration of tower members in transmission line[J]． Electric Power Construction，2014，35(5)：13-20．

[4] 李峰，袁骏． 我国输电线路铁塔结构设计可靠度研究[J]． 电力建设，2010，31(11)：18-23.

LI Feng，YUAN Jun． Research on reliability of transmission tower structure design in china[J]． Electric Power Construction，2010，31(11)：18-23．

[5] 王松涛． 现行输电塔设计规范可靠度水准的评估与分析[D]． 重庆大学，2014.

WANG Songtao． Reliability assessment and analysis of the current design code for transmission towers[D]． Chongqing University，2014.

[6] 刘静波． 输电塔结构设计表达式分项系数合理性及体系可靠度分析[D]． 重庆大学，2016.

LIU Jingbo． Rationality of partial coefficient in design expression and system reliability analysis of transmission tower[D]． Chongqing University，2016.

[7] 曹俊涵，郭晓波． 用MATLAB曲线拟合工具箱计算药物溶出度Weibull分布参数[J]． 药学进展，2006，30(12)：556-559.

CAO Junhan，GUO Xiaobo． Calculation of Weibull’s distribution parameters for drug dissolution by MATLAB curvefit toolbox[J]． Progress in Pharmaceutical Sciences，2006，30(12)：556-559．

[8] 肖郑颖． 基于MATLAB的强度分布曲线的拟合研究[J]． 湖南农机，2012，39(7)：36-36.

XIAO Zhengyin． The curve fitting research of intensity profiles based on MATLAB[J]． Hunan Agricultural Machinery，2012，39(7)：36-36．

[9] BOTEV Z I，GROTOWSKI J F，KROESE D P． Kernel density estimation via diffusion[J]． Annals of Statistics，2010，38(5)：2916-2957.

[10] DL/T 5154—2012 架空输电线路杆塔结构设计技术规定[S]. 中国计划出版社，2012.

DL/T 5154—2012 Design of latticed steel transmission structures [S]. China Planning Press,2012.

[11] 赵国藩． 工程结构可靠度[M]． 北京：水利出版社，1984.

ZHAO Guofan． Reliability for engineering structures [M]． B￣e￣i￣jing：Hydraulic Press，1984.

[12] 李继华． 建筑结构概率极限状态设计[M]． 北京：中国建筑工业出版社，1990.

LI Jihua． Probabilistic limit state design of building structures[M]． Beijing：China Architecture & Building Press，1990.

[13] 赵国藩. 工程结构可靠性理论与应用[M]． 大连：大连理工大学出版社，1996.

ZHAO Guofan. Reliability theory and its applications to engineering structures[M]． Dalian：Dalian University of T￣e￣c￣h￣n￣o￣logy Press，1996.

[14] FAN W L． Adaptive estimation of statistical moments of the responses of random systems [J]． Probabilistic Engineering Mechanics，2016，43：50-67.

[15] 范文亮，李正良，韩枫． 单变量函数统计矩的点估计法性能比较[J]． 工程力学，2012，29(9)：1-10.

FAN Wenliang，LI Zhengliang，HAN Feng． Comparison of point estimate methods for probability moments of univariate function[J]. Engineering Mechanics,2012，29(9)：1-10．

[16] 范文亮，李正良，韩枫． 多变量函数统计矩点估计法的性能比较[J]． 工程力学，2012，29(11)：1-11.

FAN Wenliang，LI Zhengliang，HAN Feng． Comparison of point estimate methods for probability moments of multivariate function[J]． Engineering Mechanics． 2012，29(9)：1-10．

[17] RAHMAN S，XU H． A univariate dimension-reduction method for multi-dimensional integration in stochastic mechanics[J]． Probabilistic Engineering Mechanics，2004，19(4)：393-408.

[18] XU H，RAHMAN S． A generalized dimension-reduction method for multi-dimensional integration in stochastic mechanics (Int．J．Numer．Meth．Engng 2004, 61：1992-2019)[J]． I￣n￣t￣e￣r￣national Journal for Numerical Methods in Engineering，2006，65(13)：2292-2292.

[19] ROSENBLATT M． Remarks on a multivariate transformation [J]． The Annals of Mathematical Statistics，1952，23(3)：470-472．