无确定性滑动面的裂隙岩体边坡潜在滑动范围确定方法及治理措施研究

(河北省高速公路管理局，河北 石家庄　050043)

0　引言

河北省自2000年以后，高速公路建设得到了极大的发展，尤其是高速公路开始从平原向山区延伸，线形指标高、路面宽、开挖量大，因而不可避免地出现了大量的高边坡。通过对张承高速、张涿高速、承赤高速和承朝高速等沿线的高边坡进行调查发现，裂隙发育型岩体高边坡在所有类型的边坡中占有较大的比例。该类型边坡的最大特点就是岩体被各种裂隙切割，降低了坡体的整体完整性，使边坡容易在外力作用下发生掉块、崩塌等地质灾害，由于边坡的裂隙分布具有随机性，较难事先明确其潜在的滑动面位置，从而给边坡的治理带来一定的难度。因此，对无确定性滑动面的裂隙岩体边坡的潜在滑动范围进行研究，并提出针对性的治理措施，具有重要的工程意义。

当前边坡稳定性的方法主要分为两类：极限平衡法和强度折减法[1]。前者是把某一个特定潜在滑动面以上的土体看作刚体，并将其划分为若干条块，假定各个条块间相互作用力方向和位置，采用一定的简化条件使之转化为静定问题，然后降低岩体强度参数使之达到极限平衡状态，通过求解静力平衡方程来得到边坡的安全系数。这种方法最大的缺陷就是需要事先假定滑动面的位置，对于裂隙发育型岩体边坡而言，假定的滑动面位置和形状较难反映真实的潜在滑动面，因而，极限平衡法不适用于该类型边坡的稳定性分析。强度折减法是边坡稳定性分析的另一种方法，是由Zienkiewicz在1975年提出的，其基本原理就是采用式(1)与式(2)不断折减岩土体的强度指标c与φ(式中，cf为折减后的粘结力，φf为折减后的摩擦角，f为折减系数)，然后进行数值分析，反复计算，直至边坡达到临界状态，此时的折减系数f即为安全系数[2]。这种方法最大的特点是不需要提前假定滑动面，可同时得出安全系数与潜在滑动面位置。因此，强度折减法可应用于此类型边坡的稳定性分析中。

(1)

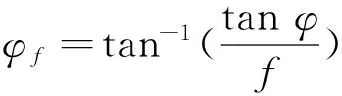
(2)

在裂隙岩体边坡的安全防护方面，挡墙是一种有效的治理措施，此种措施属于主动防护形式，既可以对坡面小范围的掉块、落石进行防护，又可以对大范围的滑塌进行治理。根据挡墙材料和支护形式，挡墙可以分为重力式挡墙、悬臂式挡墙、扶壁式挡墙、锚杆式挡墙、锚定板挡墙、加筋土挡墙、桩板式挡墙等，《公路路基设计规范》JTG D30—2015 指出锚杆挡墙宜用于墙高较大的岩质边坡，可用作抗滑挡墙[3-5]。

以承朝高速某裂隙发育型岩体边坡为研究对象，首先通过现场地质调查手段获取节理、裂隙的地质信息，并基于蒙特卡洛法模拟坡体内部节理、裂隙的分布，然后，采用强度折减法对边坡进行稳定性分析，根据滑移和张开节理的贯通状态确定边坡的滑塌范围，最后，拟采用锚杆挡墙的形式对该处边坡进行治理，并通过反复试算确定各项具体设计参数(锚杆长度、锚杆间距、锚杆直径、挡墙厚度、挡墙配筋等)。

1　蒙特卡洛法模拟随机裂隙的原理

相关研究成果表明，节理裂隙的迹场、间距通常服从负指数分布或对数型正态分布，其倾角多服从正太分布或均匀分布[6]，基于以上分布特征，可以采用蒙特卡洛法(随机模拟方法)来模拟边坡中的随机裂隙网络分布，其基本步骤如下：

(1) 根据现场地质调查结果，获得节理、裂隙的节理组数以及各个节理组的倾角、间距、岩桥长度、迹长的平均值、最小值和最大值。

(2) 建立随机变量的统计概率模型，确定与其相匹配的随机数。

(3) 通过抽样统计得到服从统计模型规律的估算值，得到与实际裂隙网络在统计特征上相同的近似网络。

(4) 利用UDEC软件重构上述随机裂隙网络。在UDEC软件中模拟随机裂隙网络的示意图见图1。设迹长为L1，岩桥长度为L2，间距为D，倾角为α；A点坐标为(Xt,Yt)，B点坐标为(Xt+1,Yt)，C点坐标为(Xt+1,Yt+1)，则有

(3)

节理A两个端点的坐标(X1,Y1)，(X2,Y2)为

(4)

2　工程地质概况

采用三维激光扫描技术，并结合地质罗盘、皮尺、相机等传统工具对该边坡进行了现场地质调查和地形测绘。根据三维激光扫描得到的效果见图2。现场地质调查发现，山体中间为冲沟，冲沟由断层经长期地质作用而成。在沟口经过人工开挖形成一个三面环坡的U型平地，并修建有3层建筑。人工开挖形成的岩质边坡呈直立状态，平均坡高约为15 m，坡体表面岩体裸露，无任何防护措施，坡体离建筑极近，约为1.5 m。边坡岩体为沉积岩，岩层呈明显的层状分布。面对建筑物，左侧坡体的坡角约为85°，平均坡高约为16 m，主要发育有4组节理，节理几何参数详见表1。右侧坡体的坡角为90°，平均坡高约为20 m，主要发育有3组节理，节理几何参数详见表2。建筑物左侧和右侧岩体的现场照片见图3。

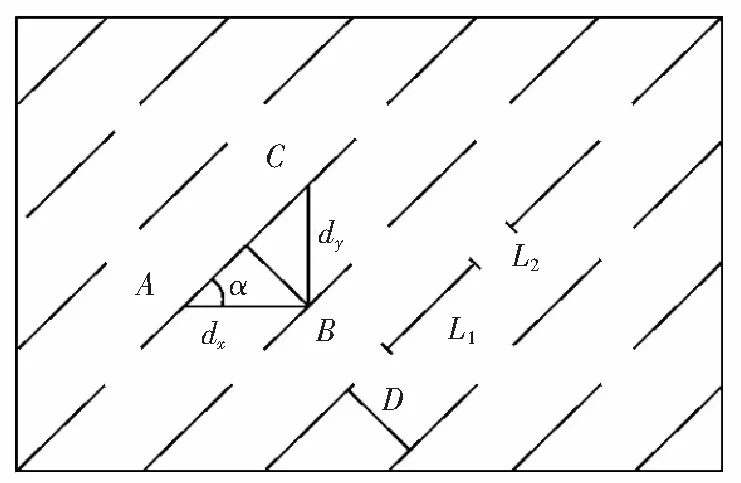
图1　节理模拟示意图[5]

图2　三维激光扫描效果图

图3　岩体现场图片

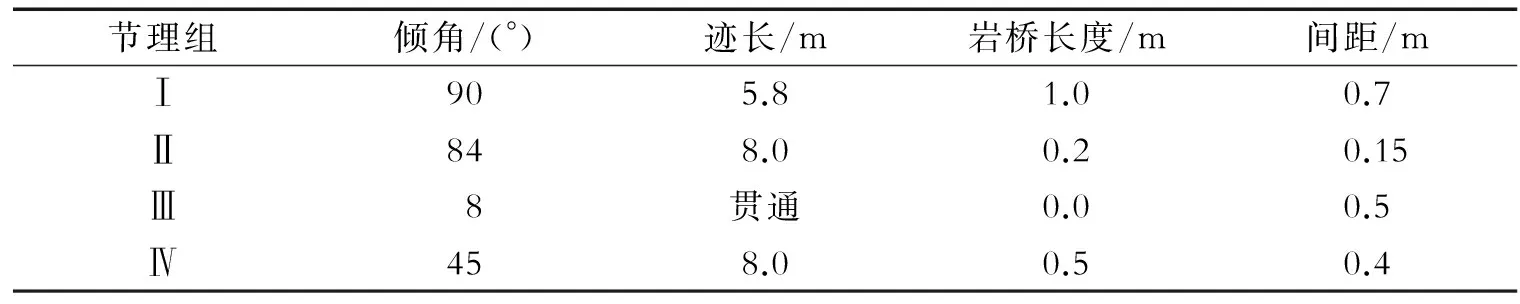
节理组倾角/(°)迹长/m岩桥长度/m间距/mⅠ905.81.00.7Ⅱ848.00.20.15Ⅲ8贯通0.00.5Ⅳ458.00.50.4

表2　右侧坡体节理几何参数(表中数据为平均值)

由于坡体表面岩体裸露，无任何防护措施，坡体离建筑极近，约为1.5 m，给建筑结构带来较大的风险，主要的安全风险问题如下：

(1) 从整体来看，边坡直立且高度较大，岩体裂隙较发育且无任何防护措施，边坡岩体在风化作用下强度进一步降低，容易发生局部掉块或者崩塌现象，随着时间的推移，有可能发生较大的边坡垮塌。

(2) 从局部部位来看，建筑结构的右边存在悬臂式危岩体，悬挑端长度约为1.0 m，且悬挑端后部存在近似贯通的竖直节理，该危岩体存在极大的崩塌风险。

(3) 建筑结构右边靠近公路的岩体发育两条张开度约为0.3～0.5 m的张拉裂缝，近似直立，且贯通，存在倾倒变形破坏的风险，给公路上的行车带来安全风险。

3　裂隙岩体边坡破坏模式及潜在滑塌范围的确定

为了评价此处裂隙岩体边坡的稳定性并确定其潜在的滑塌范围，选取4个剖面采用离散元分析方法进行分析，4个剖面的位置示意图及编号见图2。基于蒙特卡洛法和表1、表2中的统计数据，利用编写的fish语言生成4个剖面的随机裂隙网络图，见图4。由于此处岩体边坡的稳定性主要由节理、裂隙控制，因此，在分析其稳定性时，假设岩块为弹性模型，节理为弹塑性模型，采用Mohr库伦准则进行模拟。岩块和节理的力学参数如下所述：

(1) 岩块：重度为23 kN/m3，弹性模量为0.5 GPa，泊松比为0.25。

(2) 节理：法向和切向刚度为0.1 GPa，摩擦角取16°，忽略粘结力。

图4　边坡岩体的随机裂隙网络

采用强度折减法对节理的抗剪强度参数不断进行折减，并不断进行弹塑性计算，直到岩块发生明显的位移错动或者张开、滑移的裂隙呈现明显的贯通状态，此时的折减系数即为边坡的安全系数，得到边坡状态即为临界状态。4个剖面的安全系数分别是1.06、1.03、1.01、0.97，由此表明，边坡已处于临界失稳状态。把节理的强度参数除以安全系数得到新的强度参数，并重新进行弹塑性计算，由此得到4个剖面的临界状态，其临界状态的位移云图见图5。由图5可知，剖面1在重力作用下，边坡浅表层松动岩体崩落至路面，同时，在临空面后约3 m范围内存在直立的错动面，呈鼓屈、倾倒破坏形态；剖面2处浅表层松动岩体崩落至既有挡墙平台上面，同时，在临空面后约3 m范围内存在直立的错动面；剖面3处边坡岩体沿垂直主控节理发生倾覆破坏(距离初始临空面位置约为5～6 m)，进而诱发后面的岩体发生错动滑移；剖面4处边坡岩体沿倾斜节理发生滑动，从而使后缘产生张拉裂缝(张拉裂缝距离临空面约6～7 m)。

图5　临界状态破坏模式及滑塌范围

4　裂隙岩体边坡的治理措施

由第4节的分析可知，当前边坡已接近临界状态，存在较大的失稳风险，另外，根据松动岩体的范围或贯通的节理、裂隙可以确定潜在滑塌范围，为边坡的治理指明了方向。根据《公路路基设计规范》JTG D30—2015表5.4.1的建议，锚杆挡土墙宜用于墙高较大的岩质边坡，此处宜采用锚杆挡土墙进行处置。下面采用离散元分析程序对上述4个剖面的设计参数进行详细的计算分析，以使边坡达到稳定性要求。

根据《混凝土结构设计规范》GB 50010—2010和《公路路基设计规范》JTG D30—2015的相关设计要求和参数建议取值，混凝土挡墙、锚杆和注浆体的力学取值如下[3,8]：(1) 混凝土挡墙：采用C20混凝土，重度为25 kN/m3，弹性模量为25.5 GPa，泊松比为0.2，厚度为0.3 m；(2) 锚杆：HRB335螺纹钢，重度为75 kN/m3，弹性模量为200 GPa，极限抗拉强度455 MPa；(3) 注浆体：抗剪刚度0.1 GPa，抗剪强度1.5 MPa。在已知以上参数的情况下，通过离散元分析软件进行不断试算，进而确定锚杆的长度、间距以及混凝土挡墙的配筋率，其主要计算步骤如下：

(1) 根据蒙特卡洛法建立4个剖面的裂隙网络模型，见图4。

(2) 在裂隙网络模型的临空面(即坡面)设置混凝土挡墙，挡墙采用弹性模型，同时，设置锚杆并连接到混凝土挡墙上，锚杆的初始长度要穿过潜在滑塌范围区，其初始间距取《公路路基设计规范》JTG D30—2015中的建议值，与水平面呈20°倾角朝下，其初始直径取20 mm。

(3) 《公路路基设计规范》JTG D30—2015规定边坡在正常工况下的安全系数达到1.2时才符合稳定性要求，因此，对节理、裂隙网络的抗剪强度参数除以1.2后，进行弹塑性计算，判断整个边坡模型是否失稳(即锚杆是否破坏、张开和滑移的节理裂隙是否贯通、岩块是否出现滑塌)。

(4) 若此时边坡模型未发生整体破坏，则利用自编的fish语言提取混凝土挡墙的弯矩，并绘制弯矩图，用于抗弯配筋计算；若此时边坡模型发生了整体破坏，则需用重新调整锚杆的间距、长度和直径，并重新计算第(3)的计算，直到边坡达到整体稳定状态，然后再提取混凝土挡墙的弯矩。

(5) 根据第(4)步提取的弯矩对混凝土挡墙进行配筋计算。

根据以上计算步骤对4个剖面进行反复试算，最终确定4个剖面的锚杆几何参数值见表3，4个剖面的混凝土挡墙的弯矩图见图6。由图6可知，剖面1的临空面侧最大弯矩为44.63 kN·m，靠近边坡侧的最大弯矩为42.33 kN·m；剖面2的挡墙朝临空面侧弯曲，最大弯矩为31.62 kN·m；剖面3的挡墙朝临空面侧弯曲，最大弯矩为135.9 kN·m；剖面4的挡墙朝临空面侧弯曲的最大弯矩为272.4 kN·m，朝山体侧弯曲的最大弯矩为34.5 kN·m。根据《混凝土结构设计规范》GB 50010—2010，4个计算剖面均选用选用HPB235光圆钢筋作为受拉筋，保护层厚度取20 mm，抗弯配筋计算截面取2.0 m×0.3 m，由此得到4个剖面的配筋率及布筋示意图，如下所述：

剖面1：临空面一侧配筋面积为1 416 mm2(直径取10 mm，数量为18根，间距取110 mm)，靠近山体侧的配筋面积为1 416 mm2(直径取10 mm，数量为18根，间距取110 mm)，如图7(a)所示。

剖面2：临空面一侧配筋面积为1 416 mm2(直径取10 mm，数量为18根，间距取110 mm)，另外，虽然靠近山体侧不承受弯矩，但仍需要布置构造钢筋，构造钢筋采用HPB235光圆钢筋(直径取10 mm，间距取200 mm)如图7(b)所示。

剖面3：临空面一侧配筋面积为2 428 mm2(直径取10 mm，数量为31根，间距取66 mm)，另外，虽然靠近山体侧不承受弯矩，但仍需要布置构造钢筋，构造钢筋采用HPB235光圆钢筋(直径取10 mm，间距取200 mm)，如图7(c)所示。

剖面4：临空面一侧配筋面积为5 150 mm2(66根，间距取30 mm)，靠近山体侧配筋面积为1 416 mm2(18根，间距取110 mm)，如图7(d)所示。

表3　锚杆间距、长度和直径

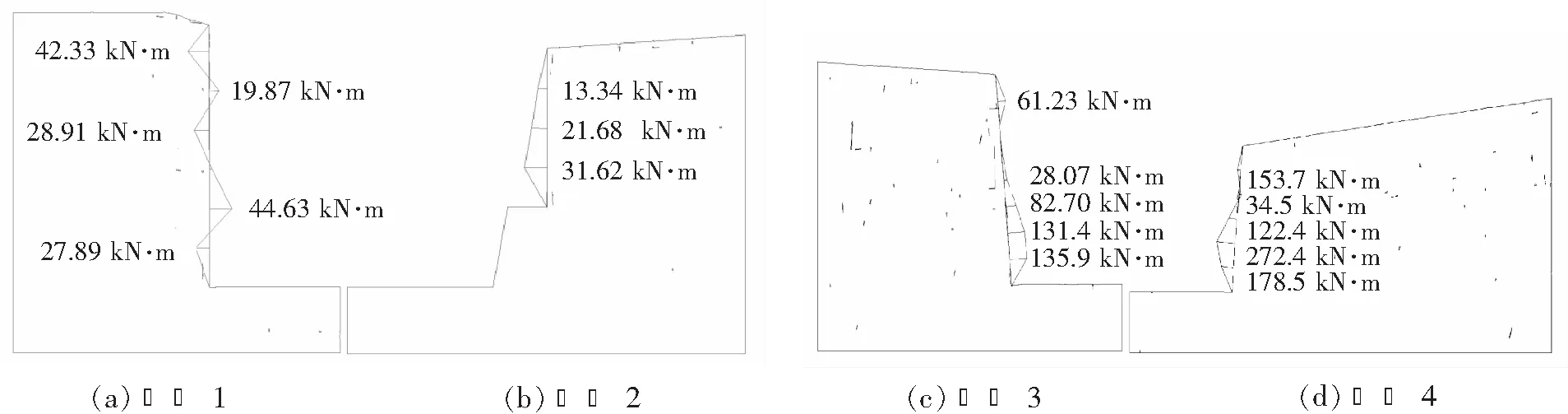
图6　混凝土挡墙弯矩图

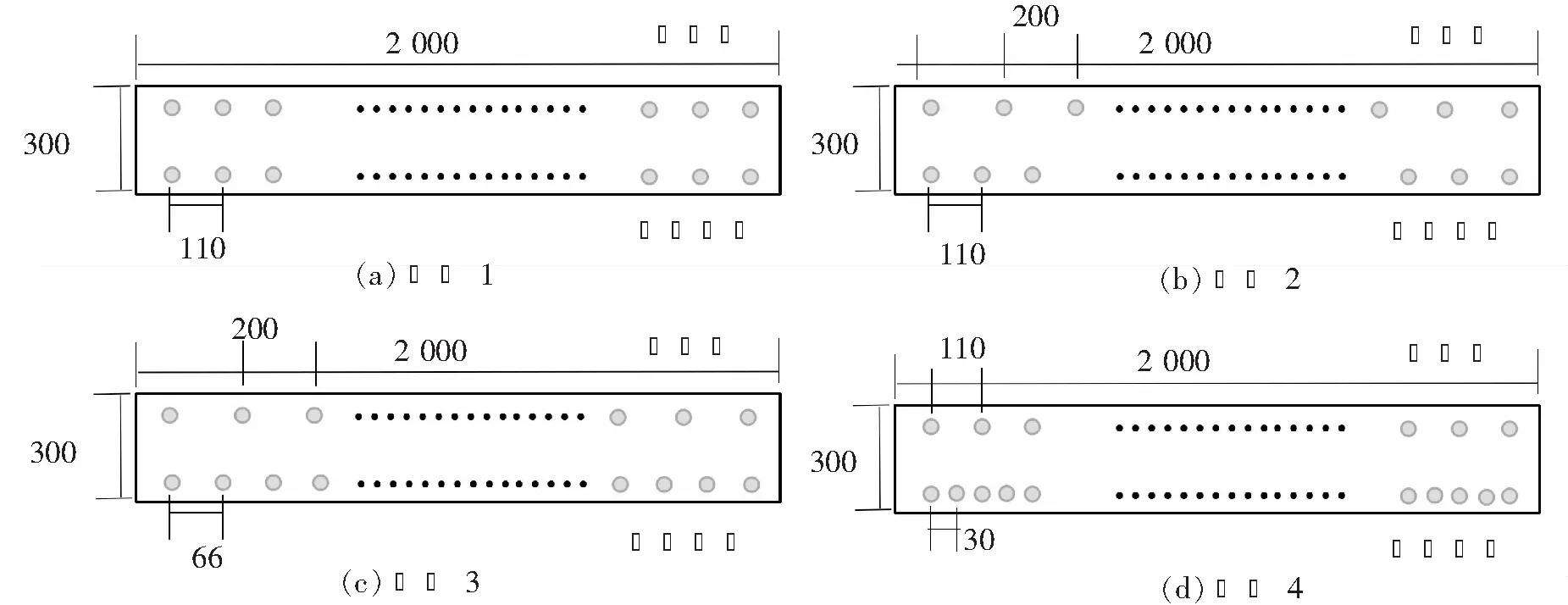
图7　混凝土挡墙纵向受力钢筋布置示意图(单位：mm)

为了验证以上设计参数的可靠性，根据以上设计参数重新建立4个剖面的地质力学模型，并把节理的抗剪切强度参数恢复到实际值，重新进行离散元分析，由此计算得到治理后4个剖面的位移变形图，见图8。对比分析图5和图8可知，采取上述治理措施后，有效地抑制了坡体表面松动岩体的掉块、倾覆和滑移破坏，提高了边坡岩体的稳定性。

图8　治理后边坡的位移变形图

5　结论

以承朝高速某裂隙发育型岩体边坡为研究对象，通过地质调查和数值模拟相结合的方法对此处边坡的稳定性进行了分析，提出了针对性的治理措施，并对具体支护参数进行了设计，取得的主要结论如下：

(1) 对于无确定性滑移面的裂隙发育型岩质边坡而言，极限平衡法较难确定其潜在滑塌范围。但是，基于离散元法和强度折减法，通过对节理、裂隙的抗剪切强度参数进行折减试算，根据张拉和滑移的裂隙呈贯通状态、岩块发生显著滑塌现象，可判断裂隙岩体边坡临界状态的潜在滑塌范围，为边坡的治理指明方向。

(2) 从治理后的数值模拟结果来看，挡墙的弯曲方向朝临空面外面，因此，在临空面外侧需要根据弯矩大小进行配筋，在临空面内侧只需根据构造要求配筋。

(3) 节理裂隙面的产状是决定裂隙岩体边坡稳定性和治理方案的一个重要影响因素，剖面1和剖面2的近似垂直节理被近似水平节理切割，而剖面3和剖面4的近似垂直节理被顺倾节理切割。因此，剖面3和剖面4中的岩体稳定性存在往临空面滑移的趋势，其稳定性比剖面1和剖面2差，其挡墙所受弯矩亦大于剖面1和剖面2。

(4) 锚杆挡墙适用于高陡岩质边坡的治理，采用离散元软件，通过反复试算确定各项设计参数(锚杆长度、锚杆间距、锚杆直径、挡墙厚度、配筋率等)，计算结果表明，锚杆挡土墙的治理方式可以有效约束住裂隙岩体的变形，同时，使裂隙岩体边坡的安全系数提高到1.2以上，符合规范的要求。因此，所设计的支护措施是合理有效的。

[1]Yuan Wei, Bai Bing, Li Xiaochun, et al. A strength reduction method based on double reduction parameters and its application[J]. J.Cent.South Univ.， 2013(20):2555-2562.

[2]袁维,胡叶江,李小春,等.一种基于位移场分析的临界滑动面确定方法研究[J].岩土力学,2016,37(6):1791-1798.

[3]吴万平. JTG D30—2015 公路路基设计规范[S].北京:人民交通出版社,2004.

[4]胡田飞.堆在诱发型滑坡变形演化机理的模型试验研究[J].石家庄铁道大学学报：自然科学版,2016,29(1):38-42.

[5]张昀青,李维珍,闫静昌,等.边坡可靠性指标及敏感性因素分析[J].石家庄铁道大学学报：自然科学版,2015,28(1):62-65.

[6]王蓬.节理岩体结构面网络模拟[D]. 上海:同济大学, 2008.

[7]杜朋召,刘建,韩志强,等.基于复杂结构精细描述的岩质高边坡稳定性分析[J].岩土力学,2013,34(s1):393-398.

[8]徐基达.GB 50010—2010 混凝土结构设计规范[S].北京:中国建筑工业出版社,2010.