考虑新旧部分协调的CFRP加固RC梁可靠度分析

，　　

(天津大学 建筑工程学院，天津　300072)

0　引言

近年来，对既有结构的加固改造受到人们的广泛关注，加固技术发展迅速[1]，采用FRP加固混凝土结构的方法越来越受到了工程界的重视[2]。Atadero et al[3]对加固桥梁结构中的桥面板的可靠度进行了分析，并通过试验确定了FRP材料的统计特征参数。孙晓燕等[4]收集了大量实验样本得到了FRP计算模式不确定性统计参数。何政等[5]对CFRP片材加固钢筋混凝土构件的可靠度指标进行了参数分析，指出了影响可靠度的主要因素。现阶段FRP加固混凝土结构可靠度的研究主要集中在将加固后RC梁原有部分和新粘贴的FRP作为整体，计算整体的抗力和作用效应并进行可靠度分析。但实际上，RC梁的破坏一般由新旧部分中可靠性较差的一部分引起，应避免结构因某一部分可靠性较低导致结构失效。当结构新旧部分可靠度保持一致或相近时，结构整体可靠性好，材料得到充分利用，加固工程也比较经济可靠。同时，建立新旧部分可靠度计算公式和分析其影响因素，对于研究加固后钢筋混凝土构件新旧部分的剩余寿命具有重要意义。

1　CFRP加固钢筋混凝土的研究

加固时受拉钢筋可能处于两种状态：已经屈服或未屈服。若钢筋已经屈服，卸载后钢筋将产生残余应变；若钢筋尚未屈服，钢筋处于弹性阶段，卸载后应变可恢复。本文的分析仅限于钢筋未屈服或残余应变较小的情况，并考虑二次受力对可靠度的影响，同时在加固设计时，为了控制加固后钢筋混凝土结构的裂缝宽度及变形，对其承载力提高幅度不超过40%。

1.1　FRP加固RC梁的破坏模式

FRP加固RC梁的破坏模式可分为以下几种主要类型：(1)混凝土被压碎引起的弯曲破坏；(2)FRP被拉断引起的弯曲破坏；(3)剪切破坏；(4)剥离破坏。规范[6]在对粘贴CFRP抗弯加固设计时规定，应避免受剪破坏先于受弯破坏发生。粘贴CFRP的目的是为了提高梁整体承载力，故设计时应保证CFRP不被拉断，对混凝土压碎的破坏模式进行分析，加固设计时为保证破坏模式为混凝土压碎，对混凝土受压区高度x进行限制，即

ξcfbh≤x≤0.8ξbh0

(1)

式中，ξcfb为碳纤维片材达到其允许拉应变与混凝土压坏同时发生时的界限相对受压区高度；ξb为构件加固前的相对界限受压区高度；h为截面宽度；h0为截面的有效高度。

1.2　钢筋混凝土构件的抗力衰减分析

建筑结构在长期使用过程中受到环境等因素影响，结构抗力将发生衰减使得可靠度降低。文献[7]对既有结构，考虑抗力随时间的衰减作用，建立了既有结构抗力衰减模型。设φc(t)为混凝土强度随时间t衰减的函数，φs(t)为钢筋强度随时间t衰减的函数，φc(t)和φs(t)均为确定性函数。

2　CFRP加固RC梁抗力和荷载分析

2.1　新旧部分的抗弯承载力计算方法

以单筋矩形截面受弯构件为例。对粘贴FRP片材进行受弯加固承载力计算时，采用规范[6]中对受弯构件正截面承载力计算的基本假定。混凝土压碎破坏模式下，RC梁破坏时，受拉钢筋已屈服，CFRP未破坏，梁破坏由混凝土压坏控制，截面应力和应变沿梁高的分布如图1所示。此时εc=εcu,εs=εy,εf<εfu。

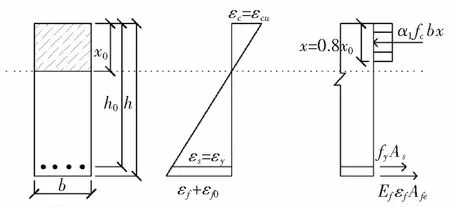
图1　受弯构件承载力极限状态时正截面计算简图

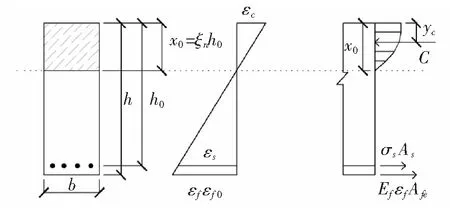
图2　给定荷载作用下受弯构件正截面计算简图

图1中εc为混凝土压应变，εcu为混凝土极限压应变，εs为钢筋拉应变，εy为钢筋屈服拉应变，εf为CFRP拉应变，εfu为CFRP极限拉应变，εf0为考虑二次受力影响时CFRP的滞后应变，α1为混凝土强度折减系数，fc为混凝土轴心抗压强度设计值，fy为钢筋屈服强度，b为截面宽度，h为截面高度，As为受拉区钢筋的截面面积，Ef为CFRP的弹性模量，Afe为CFRP的有效截面面积，x为混凝土受压区等效高度，x0为混凝土受压区实际高度。图2中，C为受压区混凝土合压力，yc为受压区混凝土合压力作用点到受压区混凝土边缘的距离，σs为受拉钢筋的应力，ξn为实际受压区高度与截面有效高度比。

由平截面假定知CFRP的应变

εf=0.8εcuh/x-εcu-εf0

(2)

式中，εf0按规范[6]取。

考虑抗力衰减的力平衡方程

φc(t)α1fcbx=φs(t)fyAs+EfεfAfe

(3)

将式(2)代入式(3)中解出x。对受压区混凝土合力作用点取矩，考虑抗力衰减的影响，对规范中的极限承载力计算公式改进，得原有部分承载力M1和新加部分承载力M2分别为

M1=φs(t)fyAs(h0-0.5x)

(4)

M2=EfεfAfe(h-0.5x)

(5)

设FRP加固后RC梁的极限抗弯承载力为Mu。显然Mu=M1+M2。

设Kp、Rp分别为计算模式的不确定性系数和结构的计算抗力，结构抗力R近似认为服从对数正态分布，计算模式不确定性变量参数取μKp=1.098,δKp=0.251[4]。根据式R=KpRp和误差传递公式可分别求得加固后原有部分和新加部分的结构抗力平均值和变异系数。

2.2　荷载分配

CFRP加固RC梁后，在给定的荷载S作用下，计算简图如图2所示。设原有部分承担荷载设计值为S1，新加部分承担的荷载设计值为S2，则有

S1+S2=S

(6)

S1=φs(t)σsAs(h0-yc)

(7)

S2=EfεfAf(h-yc)

(8)

由力平衡方程得

φc(t)C=φs(t)σsAs+EfεfAfe

(9)

由平截面假定得

(10)

对给定的荷载S，将式(7)和式(8)代入式(6)。根据应力应变关系，混凝土有εc<ε0和ε0≤εc≤εcu两种情况；钢筋有屈服和未屈服两种情况，故钢筋和混凝土的应力应变关系有4种状态，分别作4种假设。在4种假设下分别联立方程(6)、(9)和(10)，求解εc、εs、εf、ξn并检验假设是否成立，若成立即得到真值。可借助Matlab编程对该非线性方程组进行求解，将结果代入式(7)和式(8)中可得S1和S2。

2.3　荷载效应统计参数

对于承载能力极限状态，应选取永久荷载控制的荷载组合值和可变荷载控制的荷载组合值中最不利的确定，本文考虑永久荷载和一种可变荷载组合的情况，构件承载力极限状态荷载效应设计值

Sd=max{γGSGk+γQSQk,γGSGk+γQψcSQk}

(11)

式中，SGk、SQk分别为恒载、活载标准值；γG、γQ分别为恒载、活载的分项系数，当组合荷载由活荷载控制时按γG=1.2，γQ=1.4取，由恒荷载控制时按γG=1.35，γQ=1.4，γc=0.7取。

本文荷载统计特征参考文献[8]，如表1所示。

表1　结构荷载统计参数

3　CFRP加固RC梁的可靠度计算与分析

3.1　可靠度计算方法

本文仅考虑永久荷载和一种可变荷载组合的情况，得到加固RC梁的功能函数为

Z=R-SG-SQ

(12)

式中，SG，SQ分别为永久荷载效应和可变荷载效应随机变量。

JC法在可靠性分析和设计中应用广泛[9]，采用JC法求解可靠度即可得出RC梁原有部分可靠度β1和新加部分可靠度β2，本文方法取β1和β2两者较小值为RC梁结构可靠度，设βN为本文方法确定的结构可靠度，即βN=min{β1,β2}。由于β1和β2两者越相近可靠度一致性越好，故可用Δβ=|β1-β2|表示结构可靠度的一致性。为了对比分析，本文将RC梁新旧部分视为整体而得出的可靠度称为整体法可靠度，记为βZ。

表2　基本变量的统计参数

3.2　计算分析

某住宅楼已使用40a，其中某钢筋混凝土梁，梁矩形截面尺寸为b=300 mm，h=800 mm，C30混凝土，梁底部受拉钢筋为HRB335，受拉钢筋截面总面积2 945 mm2，受拉钢筋中心到梁底距离as=35 mm，加固前RC梁上原作用的弯矩标准值为M0k=200 kN·m，活荷载与恒荷载比值取ρ=0.7，弯矩设计值为560 kN·m。考虑抗力衰减影响，混凝土和钢筋的强度衰减系数为φc(t)=1.0-8.0×10-7t3，φs(t)=1.0-2.2×10-6t3，其它基本变量的统计参数见表2，用本文方法计算原有部分可靠度和新加部分可靠度，分析各参数对可靠度的影响及新旧部分可靠度协调一致性的影响。并与整体法进行对比。

3.2.2CFRP材料分项系数γf

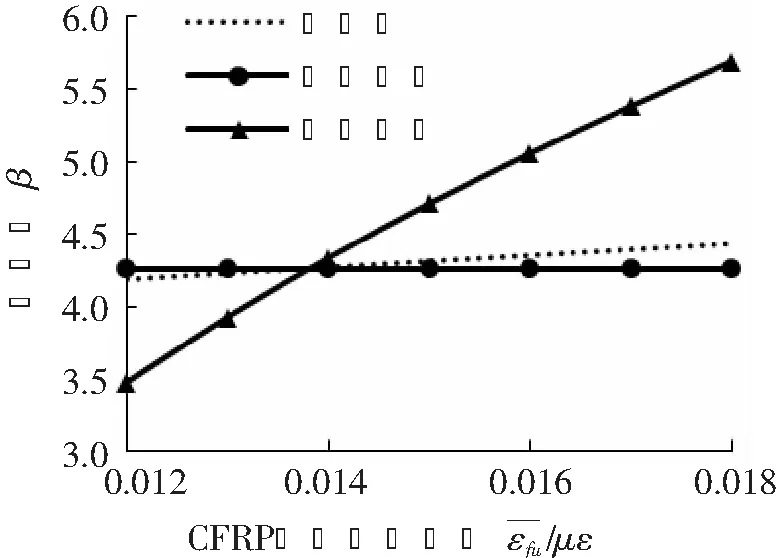
图3　CFRP极限拉应变平均值对可靠度的影响

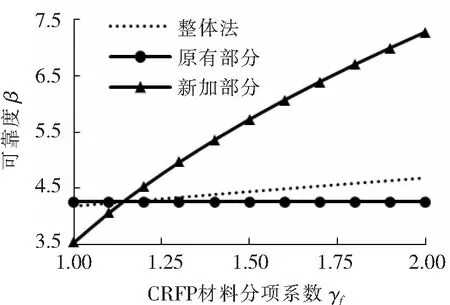
图4　CFRP材料分项系数γf对可靠度的影响

3.2.3CFRP弹性模量Ef

3.2.4CFRP配布率ρf

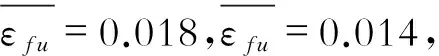
3.2.5滞后应变εf0

图5　CFRP弹性模量Ef对可靠度的影响

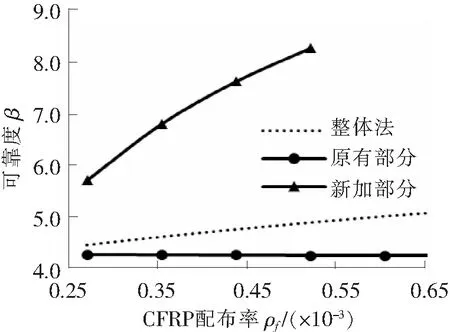
图6　CFRP配布率ρf对可靠度的影响

图7　CFRP配布率ρf对可靠度的影响

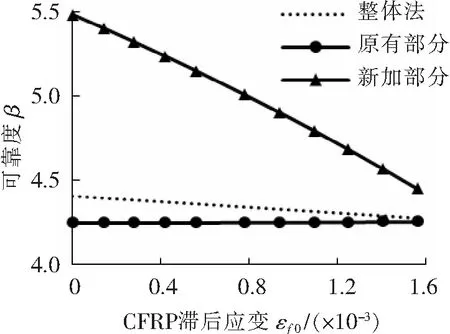
图8　滞后应变εf0对原有部分可靠度的影响

纤维种类CFRP配布率ρf/(×10-3)原有部分可靠度β1新加部分可靠度β2可靠度一致性Δβ高强度Ⅰ级CFRP布0.2344.2574.4040.147高强度Ⅱ级CFRP布0.2694.2574.3330.076高强度Ⅰ级CFRP板0.3374.2574.3430.085高强度Ⅱ级CFRP板0.3854.2574.6110.353

4　结语

对CFRP加固的RC梁，考虑加固后新旧部分的协调，分别建立了加固后RC梁原有部分和新加部分可靠度计算公式，得到了新旧部分的可靠度，给出了加固梁可靠度计算的新方法，并得出以下结论：

(3)在混凝土压碎的破坏模式下，提升CFRP的力学性能及用量，可使其达到新旧部分可靠度一致性最佳点，但继续提高其力学性能或用量并不能有效提高结构可靠度。由于结构可靠度由可靠度较低的部分控制，故粘贴CFRP加固RC梁，其可靠度的提高是有限的。

[1]蒋璐.砌体结构体外预应力加固技术设计方法及施工实现[J].石家庄铁道大学学报:自然科学版,2016,29(3):7-12.

[2]秦丽辉,王宗林.玄武岩纤维布加固损伤混凝土梁抗剪性能研究[J].石家庄铁道大学学报:自然科学版,2014,27(2):12-18.

[3]Atadero RA, Karbhari VM. Source of uncertainty and design value for field-manufactured FRP[J]. Composite Structure, 2009, 89(5):83-93.

[4]孙晓燕,黄承逵,孙保沭.既有桥梁外贴纤维布加固后可靠度分析[J].东南大学学报:自然科学版,2005,35(3):427-432.

[5]何政,李小明. FRP配筋混凝土结构可靠度设计[J].哈尔滨工业大学学报,2008,40(8):1177-1183.

[6]中华人民共和国建设部.GB50367—2013混凝土结构加固设计规范[S].北京：中国建筑工业出版社,2013.

[7]张耀华,王铁成,杨建江.考虑抗力随时间衰减的既有结构可靠度分析[J].山东农业大学学报:自然科学版,2006,37(3):429-435.

[8]史志华,胡德忻,陈基发.钢筋混凝土结构安全度水准修订评估[J].建筑科学,2002,18(2):50-57.

[9]张昀青,李维珍,闫静昌,等.边坡可靠性指标及敏感性因素分析[J].石家庄铁道大学学报:自然科学版,2015,28(1):62-65.

[10]王文炜. FRP加固混凝土结构技术及应用[M].北京：中国建筑工业出版社,2007:20-21.

[11]张建仁,毛杰,彭建新,等.使用碳纤维板加固的RC梁桥服役过程可靠度指标分析[J]. 长沙理工大学学报,2014,11(2):25-31.

[12]闫磊,任伟. FRP加固桥梁受弯构件的可靠性分析[J]. 郑州大学学报：工学版,2011,32(2):80-83.