基于神经网络的矩形钢管高强混凝土计算方法
, ,
(天津大学 建筑工程学院,天津 300072)
1 研究背景
1.1 矩形钢管高强混凝土计算理论
钢管混凝土在我国的发展速度非常快,如今已被广泛地应用到各个工程领域。矩形钢管混凝土(CFRT)除具有圆形钢管混凝土强度高、质量轻、塑性好、耐疲劳、耐冲击等优越的力学性能外,还具有节点形式简单、建筑布局灵活、截面惯性矩大、稳定性能好、施工方便、防火措施简便等优点。因此, CFRT 以其独特的力学性能在国内外高层、超高层建筑结构中已得到越来越广泛的应用。
随着建筑技术的不断发展,工程中采用的混凝土强度不断提高。一般把强度等级为C50及以上的混凝土称为高强混凝土[1]。高强混凝土具有强度高、耐久性好、变形小等优点,但是强度越高,混凝土延性越差。把高强混凝土置于钢管的约束之下,不仅能充分发挥混凝土的强度、延缓钢管的局部屈曲,而且能大大改善构件的延性、有效地防止混凝土发生脆性破坏,因此,钢管高强混凝土是一种高效结构,具有良好的应用前景[2-5]。
钢管和混凝土之间因相互约束而产生一种“效应”(图1),然而,CFRT 截面长宽不同使得对核心混凝土的侧向约束机制复杂化(图2),同时,混凝土的体积膨胀还会引起管壁的平面外弯曲变形,加上钢管残余应力、初始缺陷和局部屈曲等因素的影响,使模拟方钢管混凝土柱受力性能的工作变得非常困难。
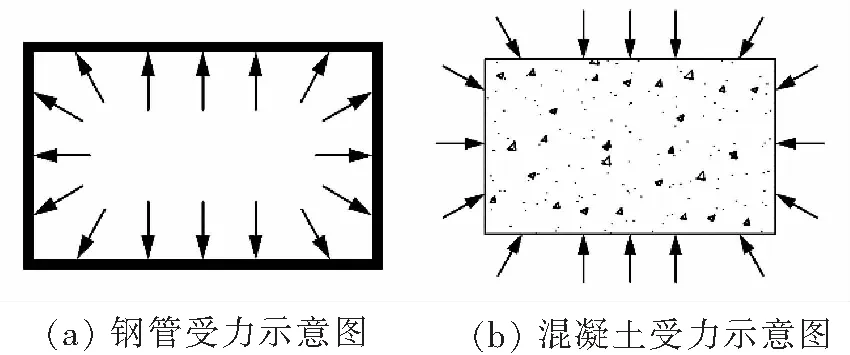
图1 矩形钢管混凝土约束示意图

图2 钢管混凝土截面的约束机制
计算矩形钢管混凝土轴向承载力的传统方法通常是先假定一个包含主要变量的经验或解析公式,然后通过对试验或数值分析结果的回归分析确定公式中未知的系数。
EC4(2004)考虑混凝土强度系数的折减[6];AISC360-10和我国的CECS159:2004均将混凝土折算成钢,把CFRT 看作受力钢构件,再按照钢结构规范的模式进行分析计算[7-8];AIJ(1997)和我国DBJ29-57—2003中没有考虑钢与混凝土之间的相互作用,只是将其强度叠加[9]。GJB 4142—2000[10]认为钢与混凝土能较好地共同工作,将CFRT视作一种组合材料,用构件整体几何特性和CFRT的组合性能指标来计算构件各项承载力。可见,由于试验以及变量选择的差异性,各个国家规范中矩形钢管混凝土的计算理论存在较大差异。各个规范中方法对于混凝土适用强度的规定不一(表1),且有的规范不适用于高强混凝土。

表1 主要规范中混凝土强度适用范围 MPa
注:国外规范均以圆柱体试件作为强度标准,国内规范均以标准棱柱体试件作为强度标准。
1.2 神经网络方法概述

图3 神经网络工作原理图
人工神经网络(Artificial Neural Networks,ANNs)简称为神经网络(NNs),它是一种模仿动物神经网络行为特征,进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度,通过调整内部大量节点之间相互连接的关系,从而达到处理信息的目的。神经网络在处理非线性复杂问题上具有突出优点,而其自学习功能对于预测有重要意义[11]。BP网络是应用最多的神经网络,可以实现从输入到输出的任意非线性映射,其基本原理见图3。
因此,许多学者在神经网络用于钢管混凝土构件的工作中进行了许多有意义的尝试[12]。朱美春[13]等将BP网络用于方钢管混凝土计算,表明其模型具有良好的学习精度和较好的泛化能力。郝艳娥[14]等用BP 网络预测矩形钢管混凝土柱的承载力,结果表明,与传统方法相比,计算简单且结果准确。Wang Haijun et al[15]对受偏压的方钢管混凝土进行神经网络模拟,预测结果准确,并且随着数据量的增加,拟合效果更好。
在总结以往研究的基础上,建立不同输入参数的2个BP神经网络模型(ANN-1,ANN-2),将其用于矩形钢管高强混凝土的预测,对比了预测结果,进而评价了神经网络模型,对影响矩形钢管混凝土承载力因素进行了分析。
2 矩形钢管高强混凝土神经网络模型
使用Matlab(R2012b)神经网络工具箱建立神经网络模型,采用基于BP 算法的多层前馈网络来进行模拟。
本文采用收集到的62组数据[16-19]中的56组进行网络模型训练, 6组数据进行预测。试件厚度范围为2~5.8 mm;混凝土轴心抗压强度标准值范围为45~81 MPa; 钢管屈服强度范围为255.1~495 MPa。网络隐含层和输出层变换函数均选择线性( purelin),采用收敛速度最快的trainlm训练算法, 取学习效率lr=0.05, 最大训练步数epochs=2 000, 控制误差goal=0.003,附加动量因子0.95。训练之前对数据做了归一化处理, 这样便于网络快速收敛。
ANN-1输入变量:①钢管截面长度h;②钢管截面宽度b;③钢管壁厚ts;④钢材强度fy;⑤混凝土强度fck。输出变量:矩形钢管混凝土柱的轴压极限强度Nu。

两个模型均采用一个20节点的隐含层,如图4所示。

图4 神经网络结构图
3 神经网络模型结果及模型验证
训练的误差随学习次数的变化曲线如图5、图6所示,ANN-1经过3次学习停止, ANN-2经过4次学习停止,误差基本趋向稳定。训练数据拟合结果见图7、图8所示,ANN-1的R值为0.945 24,ANN-2的R值为0.980 24,可见ANN-2拟合程度较高。
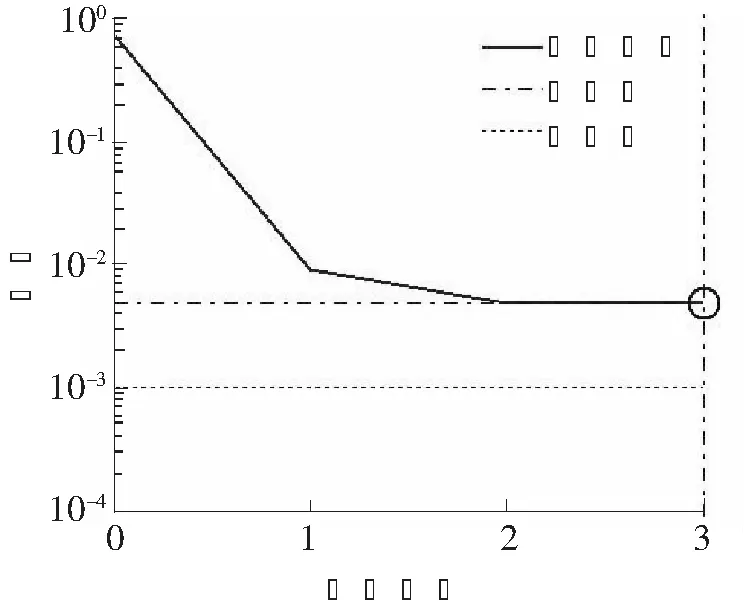
图5 ANN-1训练误差变化曲线
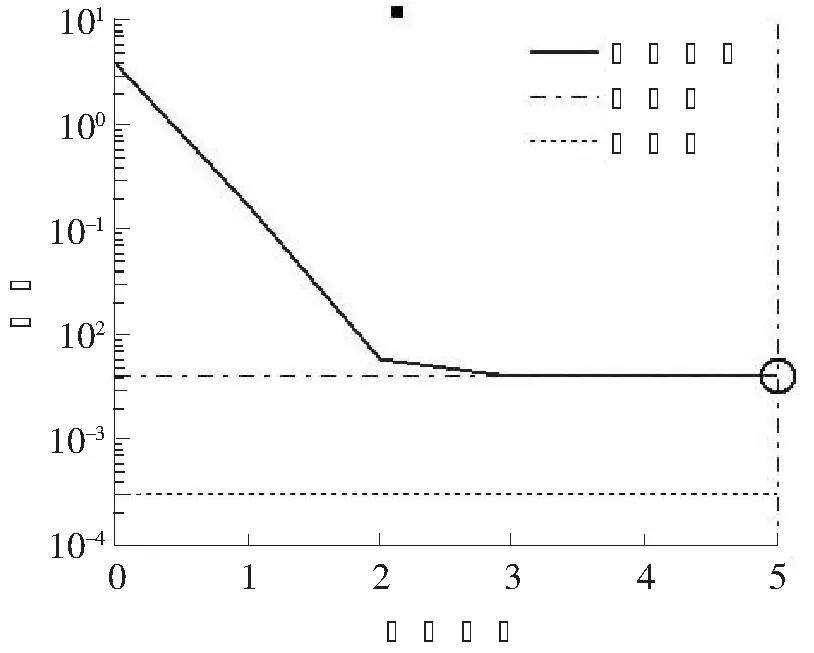
图6 ANN-2训练误差变化曲线

图7 ANN-1神经网络训练数据拟合结果
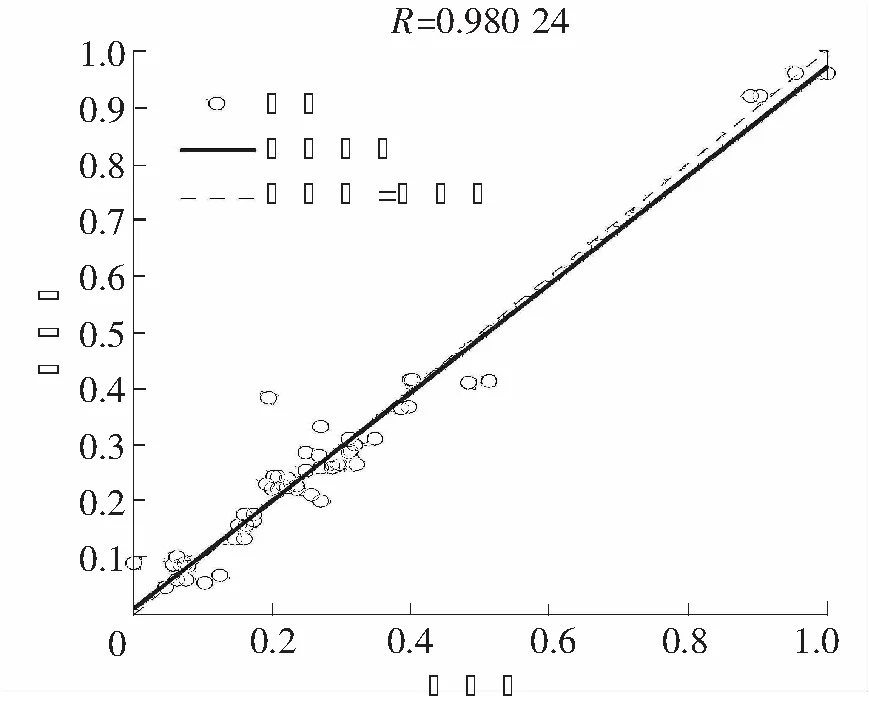
图8 ANN-2神经网络训练数据拟合结果
随后对6组来自不同文献的试验进行了预测,训练结果及与试验结果的比较见表2,结果表明, 两个神经网络模型预测误差均在允许范围之内,只有ANN-1最后一组数据的误差较大,为10.9%,其原因是由于试验条件不同,试验数据本身具有离散性,同时模型输入参数较简单,不能全面反映矩形钢管高强混凝土轴压承载力影响。
ANN-1预测平均误差为4.5%,ANN-2预测平均误差为2.2%,可见ANN-2预测效果更好,说明矩形钢管混凝土柱轴压承载力不仅与截面面积、材料强度等基本参数相关,还与长宽比、宽厚比、套箍系数和含钢率等因素有关。由于长宽比、宽厚比等不同,钢管对混凝土的约束就不同,宽厚比过小,钢管可能过早发生屈曲而降低钢管承载力。因此,矩形钢管高强混凝土的设计应当考虑钢管约束效应[20-21]。
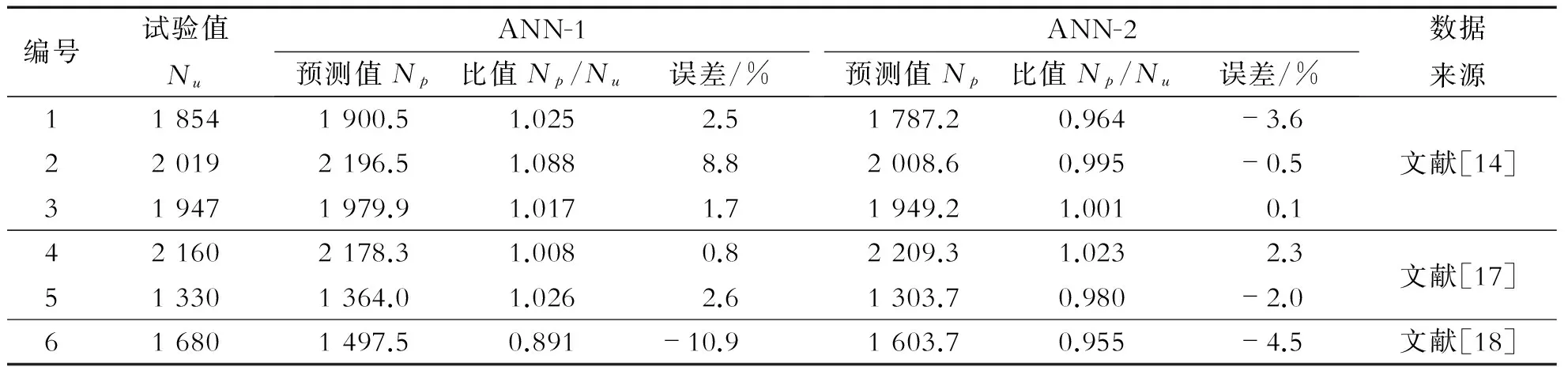
表2 ANN-1和ANN-2预测结果及误差
4 基于神经网络模型的矩形钢管混凝土参数化分析
GJB4142—2000采用基于试验回归的统一理论计算方法计算矩形钢管混凝土承载力,其公式如下
Nc=Ascfscy
(1)
式中,Asc=As+Ac;fscy=(1.212+Bξ+Cξ2)fck,B=0.138 1fy/235+0.764 6,ξ=Asfy/Ac/fckC=-0.072 7fck/20+0.021 6。
CECS159:2004中矩形钢管混凝土承载力计算公式如下
Nu=Asfy+Acfck
(2)
式中,As为钢管截面面积;Ac为混凝土截面面积;fy为钢管屈服强度;fck为混凝土抗压强度标准值。
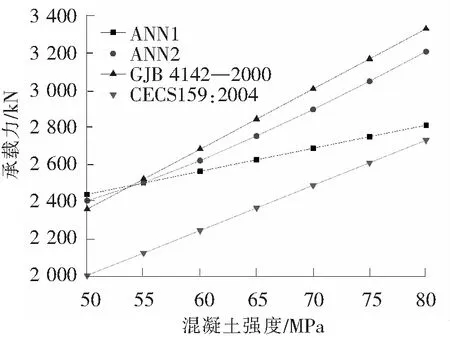
图9 参数化分析结果
利用训练好的神经网络ANN-1和ANN-2,进行了变化混凝土强度的矩形高强钢管混凝土柱的参数化分析,分析结果如图9所示。
混凝土在C50~C80范围时,CECS159:2004计算的强度最低,偏于保守。混凝土强度为C55及以下时,GJB4142—2000能够较为安全且准确地计算矩形钢管混凝土的强度,但是当混凝土强度达到C55及以上时,GJB4142—2000会高估矩形钢管高强混凝土的承载力,因此GJB4142—2000并不适用于矩形钢管高强混凝土的计算。总体来看,ANN-1和ANN-2能准确地反映承载力随混凝土强度的变化规律。
5 结论
本文建立了以不同参数为输入的神经网络ANN-1和ANN-2,用于预测矩形钢管高强混凝土的承载力。得到以下结论:
(1)基于试验数据的神经网络(ANN)模型能够准确地预测矩形钢管高强混凝土的轴压承载力;
(2)ANN-2比ANN-1预测更为准确,说明增加截面长宽比、长边宽厚比、短边宽厚比、套箍系数、含钢率等参数可以提高矩形钢管混凝土的计算精度;
(3)传统的规范不适用于采用高强混凝土的矩形钢管混凝土的计算,GJB4142—2000预测结果偏高,CECS159:2004偏于保守。
[1]中国土木工程学会高强与高性能混凝土委员会.CECS 104:99高强混凝土结构技术规程[S].北京:中国计划出版社,1999.
[2]谭克峰,蒲心诚.钢管超高强混凝土长柱及偏压柱的性能与极限承载力的研究[J].建筑结构学报,2002 ,21 (2) :12-19.
[3]周婷,李晓斐,胥民扬.方钢管混凝土组合异形柱传热性能[J].天津大学学报:自然科学与工程技术版,2015,48(增刊):74-80.
[4]蔡绍怀.我国钢管高强混凝土结构技术的最新进展[J].建筑科学,2002,18(4):1-7.
[5]王军文,王罡,张运波.钢管混凝土连续梁拱组合桥施工期拱脚应力监测与分析[J].石家庄铁道大学学报:自然科学版,2015,28(4):1-5,21.
[6] British Standards Institution.Eurocode 4, EN 1994-1-1 Design of composite steel and concrete structures.Part 1.1. General rules and rules for buildings[S]. [S.l.]:[s.n.],2004.
[7]ANSI/AISC 360-10. Specification for structural steel buildings[M]. Chicago, USA: American Institute of Steel Construction (AISC), 2010.
[8]中国工程建设标准化协会标准.CECS 159:2004矩形钢管混凝土结构技术规程[S].北京:中国计划出版社,2004.
[9]天津市地方标准.DB29-57—2003 天津市钢结构住宅设计规程[S].天津:天津市建设管理委员会,2003.
[10]国家军用标准.GJB4142—2000战时军港抢修早强型组合结构技术规程[S].北京:中国人民解放军总后勤部,2001.
[11]张德丰.MATLAB神经网络应用设计[M].北京:机械工业出版社,2012:37-50.
[12]邵成猛.基于盾构掘进参数的LVQ神经网络地层识别[J].石家庄铁道大学学报:自然科学版,2016,29(1):93-96,102.
[13]朱美春,王清湘,冯秀峰.方钢管混凝土短柱轴心受压承载力的神经网络模拟[J].计算力学学报,2006(3):252-255.
[14]郝艳娥, 翟振东.矩形钢管混凝土短柱轴压承载力神经网络评估[J].长安大学学报,2004,1(3):24-28.
[15]Wang Haijun, Zhu Huabei, Wei Hua. Bearing capacity of concrete filled square steel tubular columns based on neural network[J]. Advanced Materials Research ,2012,502:193-197.
[16]Liu Dalin, Gho Wiemin. Axial load behavior of high-strength rectangular concrete-filled steel tubular stub columns [J]. Thin-Walled Structures, 2005, 43: 1131-1142.
[17]张素梅,郭兰慧,叶再利,等.方钢管高强混凝土轴压短柱的试验研究[J].哈尔滨工业大学学报,2004,36(12):1610-1614.
[18]郭兰慧, 张素梅.截面长宽比对矩形钢管高强混凝土轴压构件的影响[J].哈尔滨工业大学学报,2003,35(增刊):155-159.
[19]Liu D. Tests on high-strength rectangular concrete-filled steel hollow section stub columns[J]. Journal of Constructional Steel Research, 2005, 61(7): 902-911.
[20]Lam D, Williams C A. Experimental study on concrete filled square hollow sections[J]. Steel and Composite Structures, 2004, 4: 95-112.
[21]Liu D, Gho WM, Yuan J. Ultimate capacity of high-strength rectangular concrete-filled steel hollow section stub columns[J]. Journal of Constructional Steel Research, 2003, 59(12): 1499-1515.

