并列双钝体箱梁三分力系数的气动干扰效应
, , ,
(1. 石家庄铁道大学 大型结构健康诊断与控制研究所,河北 石家庄 050043;2. 河北省大型结构健康诊断与控制重点实验室,河北 石家庄 050043;3. 石家庄铁道大学 土木工程学院,河北 石家庄 050043)
0 引言
三分力系数是表征桥梁风荷载的一组无量纲参数,它既是反映桥梁静风荷载的重要指标,也是分析桥梁气动问题的基础。为了准确获取三分力系数,研究者们通过风洞试验或数值模拟手段对不同断面外形的主梁进行了大量研究,并形成了一些规范条文[1],但目前的研究成果及相关规范主要是针对单幅主梁展开的。近年来,随着交通流量的逐渐增大,在一系列大跨桥梁的设计及修建过程中,具有上下行分离的双主梁桥不时出现。由于间距不大,这类桥梁两分离主梁之间存在气动干扰效应,上下游主梁的三分力系数不同于单主梁的三分力系数。对于双主梁桥三分力系数的气动干扰效应,已有一些研究者开展了相关研究。
刘志文等针对佛山平胜桥和青岛海湾大桥红岛航道桥开展了双主梁三分力系数的气动干扰效应研究[2-4],结果表明,气动干扰对阻力系数的影响较大,对升力系数和扭矩系数的影响很小。郭震山等针对某斜拉桥的改扩建工程,在引入气动干扰因子的基础上分析了既有桥梁对其临近的新建桥梁三分力系数的影响[5],结果表明,阻力系数干扰因子随着风攻角绝对值的增大而增大,升力系数干扰因子随风攻角的增加呈递减的趋势,扭矩系数干扰因子随风攻角的变化规律不明显。曲慧等以崇启大桥为背景,试验研究了分离双箱梁三分力系数的气动干扰效应[6],结果发现,两分离箱梁的三分力系数存在非常显著的相互干扰效应。郭春平等以陕西省咸阳市至旬邑县高速公路段的三水河大桥为背景,对6种不同间距下双分离主梁的三分力系数进行了数值计算,并与单幅主梁的结果进行了对比[7],研究发现,与单幅主梁相比,上游主梁的三分力系数变化不大,下游主梁的阻力系数和升力系数降低幅度很大,间距越小,降低幅度越大。
综合以上文献可以看到,目前分离双主梁三分力系数的气动干扰效应研究大部分都是针对实际的桥梁工程,在特定的间距下开展的。由于参数变化较少,所得的研究结果尚难以准确系统地认识分离双主梁三分力系数的气动干扰规律,十分有必要对这一问题开展进一步的深入研究。现针对近年来在分离双主梁桥中经常采用的一类双钝体箱梁,在15个不同的间距下进行了三分力的风洞测试,并将结果与单箱梁的结果进行了对比,详细地分析了三分力系数的气动干扰效应。
1 风洞试验概况
如图1所示,两钝体箱梁模型的尺寸一致。单幅箱梁模型宽B=370 mm,高H=110 mm,长L=2 000 mm。模型由ABS板制成,在上下游模型的中央位置沿周向各布置一圈测压孔,每圈共60个测点。考虑到模型棱角附近的流动参数变化比较剧烈,这些位置的测压孔相对密集。
如图2所示,风洞试验在石家庄铁道大学风工程研究中心STU-1风洞低速试验段中进行。该试验段长24 m,宽4.4 m,高3 m。首先进行单箱梁模型试验,然后进行并列双箱梁模型试验。对于并列双箱梁模型,选择了D/B(D为两模型的净间距,B为单幅模型的宽度)为0.025、0.05、0.075、0.1、0.2、0.3、0.4、0.6、0.8、1、2、3、4、5、6的15个间距进行试验研究。试验流场为均匀流场。为了避免模型的局部位置发生振动,提高试验精度,来流风速为6 m/s,以模型宽度B为特征尺寸定义的雷诺数为1.48×105。模型表面不同位置测压孔的风压通过电子压力扫描阀测得,电子压力扫描阀的采样频率为330 Hz,采样时间为30 s。

图1 试验模型的尺寸及测点布置(单位:mm)

图2 双箱梁模型试验照片

图3 箱梁模型的三分力
2 气动干扰效应试验结果
2.1 双箱梁三分力系数随间距的变化
在来流风作用下,箱梁模型单位长度上的顺风向阻力FD,横风向升力FL及绕中心的扭矩MT如图3所示。该三分力可通过对模型表面各测点的压力进行积分得到。
三分力系数定义如下
CD=2FD/ρU2B
(1)
CL=2FL/ρU2B
(2)
CM=2MT/ρU2B2
(3)
式中,B为模型的宽度;U为来流风速;ρ为空气密度,取1.225 kg/m3。
图4给出了双箱梁的三分力系数随无量纲间距D/B的变化曲线,并与单箱梁的结果进行了对比。
从图4(a)可以看到:(1)单箱梁的阻力系数约为0.34;(2)上游箱梁的阻力系数与单箱梁的阻力系数比较接近,仅在D/B<0.1的小间距时略大于单箱梁的阻力系数;(3)下游箱梁的阻力系数在D/B<1.0时为负值,随着间距的增大,阻力系数由负值变为正值,并逐渐增大,但即使当D/B=6时,其值还是比单箱梁的阻力系数小,约为0.28。从图4(b)可以看到:(1)单箱梁的升力系数约为0.82;(2)上游箱梁的升力系数与单箱梁的升力系数比较接近,仅在D/B<0.1的小间距时略小于单箱梁的升力系数;(3)下游箱梁的升力系数在D/B=0.025时约为-0.3,随着间距的增大,升力系数逐渐增大,当D/B=6时,约为0.12,仍远小于单箱梁的升力系数。从图4(c)可以看到:(1)单箱梁的扭矩系数约为0.16;(2)上游箱梁的扭矩系数与单箱梁的扭矩系数比较接近;(3)下游箱梁的扭矩系数在D/B=0.025时约为-0.03,随着间距的增大,扭矩系数呈现出先减小后增大的变化趋势,在D/B=0.3时达到最小值,约为-0.05,在D/B=6时达到最大值,接近单箱梁的扭矩系数。

图4 单箱梁及不同间距双箱梁的三分力系数
2.2 双箱梁三分力系数干扰因子随间距的变化
为了定量地分析双箱梁三分力系数的气动干扰效应,采用下式定义三分力系数的气动干扰因子
(4)
式中,IFSD为上游箱梁阻力系数干扰因子;IFSL为上游箱梁升力系数干扰因子;IFSM为上游箱梁扭矩系数干扰因子;IFXD为下游箱梁阻力系数干扰因子;IFXL为下游箱梁升力系数干扰因子;IFXM为下游箱梁扭矩系数干扰因子。干扰因子大于1,表示气动干扰为增大效应;干扰因子小于1,表示气动干扰为减小效应。
图5给出了上、下游箱梁的三分力系数干扰因子随间距的变化曲线。
从图5(a)可以看到:(1)上游箱梁阻力系数干扰因子IFSD大体接近1,仅在D/B<0.1的小间距时略大于1,最大值为1.17左右;(2)下游箱梁阻力系数干扰因子IFXD均小于1,变化范围为-0.25~0.83,在D/B=6时达到最大值,间距越小,干扰因子越小。这表明:气动干扰对上游箱梁阻力系数的影响很小,仅在D/B<0.1的小间距时略有影响,表现为放大效应;气动干扰对下游箱梁阻力系数的影响很明显,表现为减小效应,间距越小,这种减小效应越显著。
从图5(b)可以看到:(1)上游箱梁升力系数干扰因子IFSL大体接近1,仅在D/B<0.1的小间距时略小于1,最小值为0.69左右;(2)下游箱梁升力系数干扰因子IFXL均小于1,变化范围为-0.37~0.14,在D/B=6时出现最大值,随着间距的变小,干扰因子逐渐变小。这表明:气动干扰对上游箱梁升力系数的影响很小,仅在D/B<0.1的小间距时略有影响,表现为减小效应;气动干扰对下游箱梁升力系数的影响很大,表现为减小效应,间距越小,这种减小效应越显著。
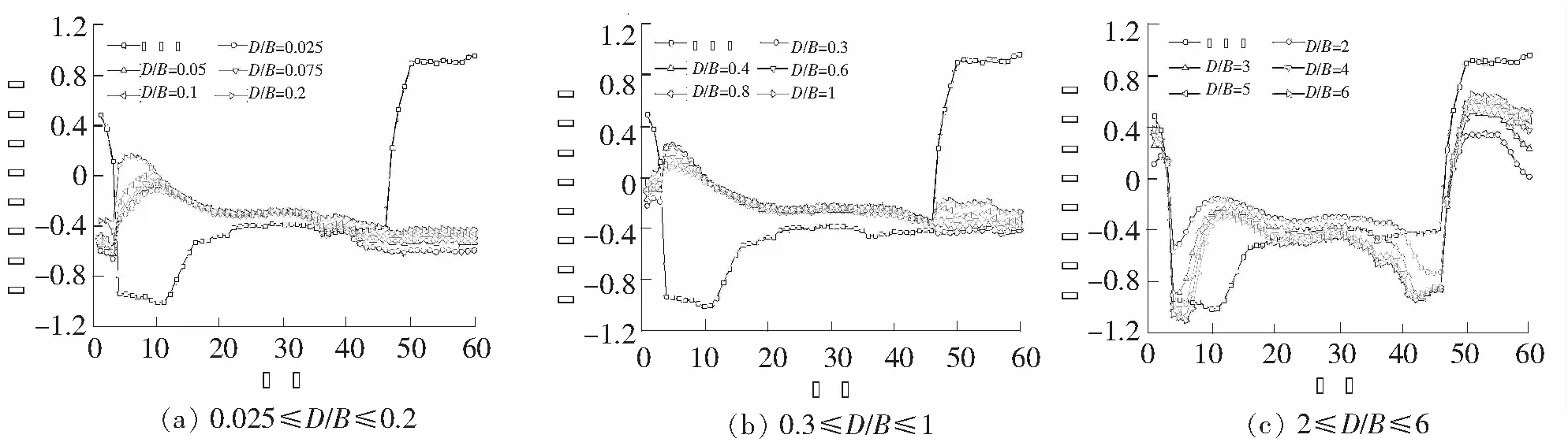
从图5(c)可以看到:(1)上游箱梁扭矩系数干扰因子IFSM的变化范围为0.92~1.07,基本接近1;(2)下游箱梁扭矩系数干扰因子IFXM均小于1;在0.025 图5 不同间距双箱梁的三分力系数干扰因子 从微观角度看,并列双钝体箱梁三分力的变化源于其表面各局部位置风压的变化,因此,下面从双箱梁表面风压系数分布的角度来解释三分力系数的气动干扰效应。考虑到气动干扰效应主要表现为对下游箱梁的影响,因此下面主要针对下游箱梁进行解释。 图6给出了不同间距时下游箱梁表面各测点的风压系数,并与单箱梁表面各测点的风压系数进行了对比。图中风压系数的正负号意义如下:正号表示风压沿模型表面法向向内,即对表面产生压力;负号表示风压沿模型表面法向向外,即对表面产生吸力。 图6 单箱梁及不同间距时下游箱梁各测点的风压系数 从图6可以发现:(1)下游箱梁表面测点风压系数与单箱梁表面测点风压系数的差异主要集中于迎风直面(测点1~3和测点47~53)、上表面(测点4~18)和迎风斜面(测点54~60)。(2)单箱梁迎风直面各测点的风压系数为正值,表明迎风直面受到顺风向的压力作用,方向与图3中定义的阻力正方向一致。下游箱梁迎风直面各测点风压系数在较大间距时虽然也为正值,但小于单箱梁的风压系数,随着间距的减小,其值不断减少,在小间距时甚至出现了负值。这说明,下游箱梁迎风直面受到的顺风向压力偏小,间距越小,压力越小,在小间距时甚至出现了逆风向的吸力,这是下游箱梁阻力系数小于单箱梁阻力系数,间距越小,减小幅度越大的主要原因。(3)单箱梁上表面各测点的风压系数为负值,表明上表面受到向上的吸力作用,方向与图3中定义的升力正方向一致。与单箱梁相比,下游箱梁上表面各测点风压系数虽然也为负值,但绝对值明显小于单箱梁的风压系数绝对值,间距越小,减小幅度越大,因此,其受到的向上吸力减小,间距越小,吸力越小,这是下游箱梁升力系数小于单箱梁升力系数,间距越小,减小幅度越大的一个原因。单箱梁迎风斜面各测点的风压系数为正值,表明迎风斜面受到向上的压力作用,方向与图3中定义的升力正方向相同。与单箱梁相比,下游箱梁迎风斜面各测点风压系数在较大间距时虽然也为正值,但小于单箱梁的风压系数,随着间距的减小,风压系数变小,因此,其受到的向上压力偏小,间距越小,减小的幅度越大,这是下游箱梁升力系数小于单箱梁升力系数,间距越小,减小幅度越大的另一个原因。(4)从单箱梁的风压系数分布可以看到,对扭矩起主要贡献的两个位置为上表面的迎风端(测点4~11)和迎风斜面(测点54~60)。上表面迎风端受到的向上吸力和迎风斜面受到的向上压力对断面中心产生的扭矩为顺时针方向,与图3中定义的扭矩正方向一致。从以上的分析可以看到,下游箱梁上表面迎风端受到的向上吸力小于单箱梁对应位置的吸力,迎风斜面受到的向上压力小于单箱梁对应位置的压力,这必然导致这两位置对断面中心产生的顺时针方向的扭矩偏小,此为下游箱梁扭矩系数小于单箱梁扭矩系数的主要原因。 针对并列双钝体箱梁开展了节段模型测压风洞试验,研究了在D/B=0.025~6(D为双箱梁的净间距,B为单箱梁宽)之间15个不同间距下的三分力系数,并与单幅钝体箱梁的三分力系数进行了对比,主要得到了以下几点结论: (1)气动干扰对上游箱梁阻力系数和升力系数的影响很小,仅在D/B<0.1时略有影响,分别表现为增大效应和减小效应。气动干扰对上游箱梁扭矩系数的影响基本可以忽略。 (2)气动干扰对下游箱梁阻力系数和升力系数的影响比较明显,均表现为减小效应,间距越小,减小幅度越大。气动干扰对下游箱梁扭矩系数的影响比较明显,表现为减小效应,在0.025 (3)建立了并列双钝体箱梁三分力系数气动干扰效应的定量研究方法,给出了三分力系数的干扰因子随间距的变化曲线,可为实际工程中并列双钝体箱梁桥的抗风设计提供参考。 [1]中交公路规划设计院. 公路桥梁抗风设计规范[M].北京: 人民交通出版社, 2004. [2]刘志文, 陈政清, 刘高. 双幅桥面桥梁三分力系数气动干扰效应试验研究[J]. 湖南大学学报, 2008, 35(1): 16-20. [3]陈政清, 刘小兵, 刘志文. 双幅桥面桥梁三分力系数的气动干扰效应研究[J]. 工程力学, 2008, 25(7): 87-93. [4]陈政清, 牛华伟, 刘志文. 双幅桥面桥梁主梁气动干扰效应研究[J]. 桥梁建设, 2007(6): 9-12. [5]郭震山, 孟晓亮, 周奇,等. 既有桥梁对邻近新建桥梁三分力系数的气动干扰效应[J]. 工程力学, 2010, 27(9) : 181-186. [6]曲慧, 马如进, 陈艾荣. 分离式钝体钢箱梁静气动力节段风洞试验研究[J]. 结构工程师, 2010, 26(3): 89-94. [7]郭春平, 白桦, 洪光. 双幅桥静分力系数气动干扰效应研究[J]. 重庆交通大学学报:自然科学版, 2011, 30(5): 899-902.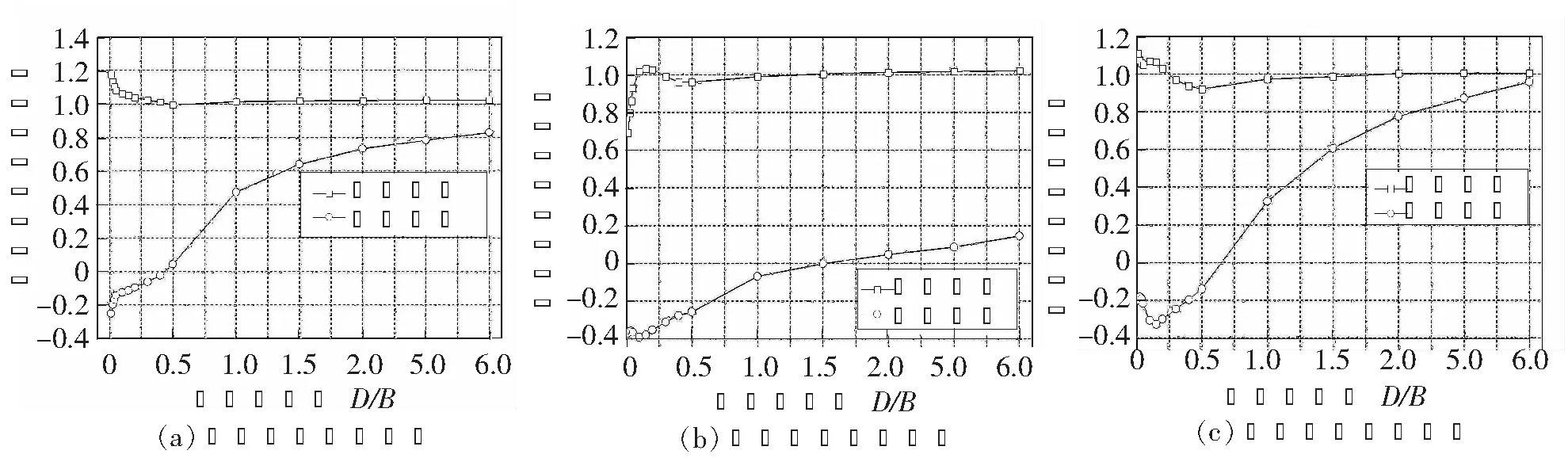
3 气动干扰效应的微观解释
4 结论

