基于蒙特卡洛仿真的金丝键合宽带匹配研究
, ,
(中国电子科技集团公司 第五十四研究所,河北 石家庄 050081)
0 引言
随着微波、毫米波电路向着小型化、高集成度的方向发展,金丝键合工艺已经越来越多地应用于微波射频器件的信号互联中,典型应用场景包括芯片—芯片、芯片—传输线间的信号传输等[1]。在射频电路中,金丝的引入会引起射频电路性能的恶化,工作频率越高,对电路性能的影响越明显。对改善金丝键合射频特性的研究主要集中于两个方面:一是通过改变金丝的数量和形状以减少金丝键合不连续性带来的射频性能恶化,二是优化与金丝相连的电路参数或电路图型,以对金丝键合引入的寄生参数进行补偿。对于金丝形状和数量的优化已经非常充分,得出多项有价值的结论,包括通过增加金丝根数来改善传输性能[2],降低金丝拱高和减小跨距来优化电路性能[3],以及在使用两根金丝的情况下通过改变金丝间角度以改善电路性能[4]等。通过电路参数和形状匹配补偿金丝键合不连续性的方法则包括L网络集总元件匹配、单短截线匹配、双短截线匹配和多节匹配等[5]。以上补偿手段都是通过确定性方法,针对特定的金丝落点进行匹配。
混合微波电路往往有套量小,结构复杂的特点,出于成本考虑,通常会采用人工键合的方式完成芯片与传输线器件间的互联。尽管在小批量任务上人工键合有很大的成本优势,但其弊端也很明显:人工键合精度无法和自动键合机相比,不同人员的操作水平也存在明显差距,尽管设计师可以优化出最好的键合方式,但按照预先给定的位置进行键合几乎不可能实现。在以往金丝键合优化的研究中,通常不考虑人工键合造成的数据离散,或者直接将其视作背景误差,这样做出的优化往往不是全局最优的。为此,本文提出了一种新的方法进行补偿,即基于蒙特卡洛仿真的金丝键合宽带匹配方法,以解决人工键合带来偏差的问题。
蒙特卡洛方法是一种计算方法,但与一般数值计算方法有很大区别。它是以概率统计理论为基础的一种方法[6]。蒙特卡洛方法能够比较逼真地描述事物的特点及物理实验过程,解决一些数值方法难以解决的问题[7]。
基于蒙特卡洛仿真的金丝键合宽带匹配方法,能够在不确定的情况下寻求一种精确的匹配,它首先统计若干人工操作的键合线的落点的数据,并计算出其统计特征值,然后建立一种与实际操作过程有相同的统计参数的概率化的金丝落点的数学模型,以复现人工打丝的过程。这种方法在金丝匹配的研究中通用性更强。
1 金丝键合模型分析
1.1 金丝键合等效电路分析
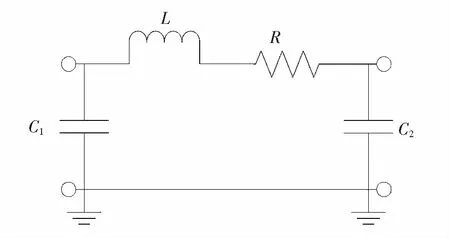
图1 金丝键合不连续结构等效电路图
使用金丝键合的传输线互连结构可等效为一个串联电阻R、一个串联电感L和两个旁路电容C1、C2组成的低通滤波器网络,如图1所示[8]。在该模型中,起主要作用的是键合线串联电感L, 而并联电容C1、C2和串联电阻很小, 所以常常忽略并联电容以及串联电阻的影响。模型可以简单等效为一只电感[9]。通常可使用一个容性结构来匹配电感。
1.2 传输线试验板的改进
首先通过测量传输线试验板上的金丝落点以获取人工打丝的金丝落点数据。以往传输线试验板的加工制造,是将两片带有微带线的印制板用导电胶安装于屏蔽盒内,在两块印制板之间留出一定间隙进行打丝,但两印制板之间的距离受装配工艺限制,对位精度很难保证,这就造成了试验可重复性差的问题。利用盲槽工艺针对这一环节进行了改良,即将两段微带线置于一整块多层印制板上,在印制板的两微带线之间处挖一个盲槽,并在传输线槽的两侧打丝,利用印制板更高的加工精度改善装配过程造成的额外的不一致性。
所谓盲槽工艺,是为了满足信号完整性以及信号接收与屏蔽匹配性等要求,在PCB制作时利用已经钻好槽孔板和半固化片与另一张板进行压合[10]。盲槽的具体制作方式为:先将低流动半固化片及相应芯板按要求铣出空槽,再直接压合而成[11]。
使用盲槽设计除改善试验一致性问题外,还可有效提高印制板的机械强度,从而对可测试性做出改善。本文采用的0.254 mm厚的Rogers Duroid 5880材质较软,若单独使用存在机械强度不够的问题,没有屏蔽盒的支撑保护将无法进行测试。所以采用了将Rogers Duroid 5880与FR-4混压的方式来增加强度,如图2所示。这种盲槽加混压的加工方式既提高了加工的一致性又省去了加工屏蔽盒的程序。
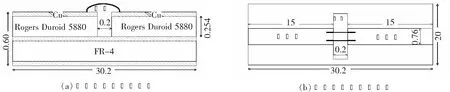
图2 金丝键合模型侧视图和金丝键合模型俯视图(单位:mm)
2 基于蒙特卡洛方法的金丝补偿与电容参数提取
2.1 蒙特卡洛补偿原理
蒙特卡洛仿真是一种能够在无法准确获取变量信息的情况下,对样本进行近似分析得到变量信息特性的方法,它是一种试验数学方法,利用随机数进行统计检验,以求得的统计特征值(如均值、方差、概率等)作为待解问题的数值解,并借助于概率化的数学模型和被研究实际问题的物理过程的统计特征计算以复现该过程的方法。该方法能对建立的数学模型进行多次试验,并以此为基础对试验数据做统计处理,得出被研究过程的特征,作为过程参数的统计估计值。根据这些参数的散布量,能够从概率意义上确定解决问题的近似程度[12]。
一般两根金丝键合互连的微波特性优于单金丝键合互连。所以,本次所匹配的金丝线模型为两根金丝线键合互连[5]。在用两根金丝进行键合的情况下,两金丝之间的距离变化会引起连接线之间互感系数的变化,对传输线的传输性能有一定影响[5]。而金丝之间距离的变化主要体现在金丝落点位置的变化。在人工打线的实际操作中,对金丝落点的控制不可能分毫不差,人工打线的实际金丝落点与之前仿真设定存在偏差,从而致使之前的匹配不准,影响微带线的信号传输。为了规避人工操作造成的不可避免的手工误差,利用蒙特卡洛法对金丝进行补偿,即提前考虑到金丝落点的不确定性,在落点不确定的前提下寻求一种最优的补偿。
2.2 统计参数提取
为了准确模拟人工打丝情况,首先要了解工人在已经知道金丝的焊接位置的前提下实际打出的金丝落点的离散性。为此加工了10套前述使用盲槽结构的传输线试验板,让工人以预先指定的落点位置为目标打丝,印制板实物图如图3所示。基板材质如前文,为Rogers Duroid 5880和FR-4混压基板,基板尺寸为30.2 mm×20 mm。微带线宽度为0.76 mm,微带线间距0.2 mm。
预设的4个落点A、B、C、D的坐标分别为A(-0.2,0.25)、B(-0.2,-0.25)、C(0.2,0.25)、D(0.2,-0.25),单位为毫米。坐标原点如图4所示为微带线缝隙中心点。对10块试验板的所有金丝落点进行测量并分别计算其均值和方差,与提前设定的目标值进行对比,如表1所示。金丝落点和目标值及均值的分布情况如图5所示。可以看出,实际落点位置与目标值的确存在一定偏差,且都落在一定范围内。

图3 匹配前传输线试验板实物图
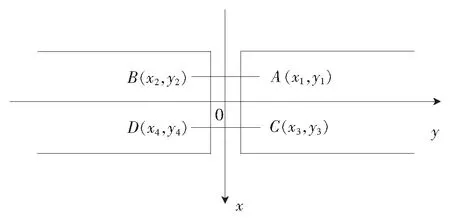
图4 金丝落点示意图

统计参数x1y1x2y2x3y3x4y4目标值 -0.20000.2500-0.2000-0.25000.20000.25000.2000-0.2500实测值均值 -0.19650.2350-0.2135-0.24500.18650.23000.1920-0.2480实测值方差 0.00210.00140.00300.00060.00390.00080.00560.0007实测值标准差0.04600.03700.05500.02400.06200.02800.07500.0260
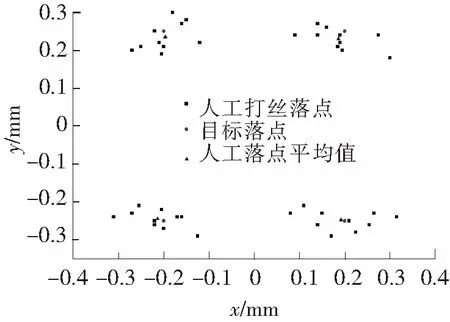
图5 目标值与实测值对比图
3 基于蒙特卡洛法的金丝键合宽带匹配的实现
3.1 软件平台
HFSS 是ANSYS的一款电磁场仿真软件,采用有限元法来解决微波电路的问题。可直接利用HFSS中的键合线模型修改键合线的各项参数来完成仿真。从而了解键合线参数变化对信号传输的影响。
VBScript是一种Windows脚本,是微软公司出品的一套可视化编辑工具,语法基于Basic。作为一种编程语言,VBScript也有循环语句的概念,因此可以在编写HFSS脚本语言时,使用VBS语言中的循环语句编写微波器件模型中的重复结构,直接点击VBS文件即可运行HFSS,在HFSS中自动生成该模型,这简化了建模过程中的很多重复的手动修改过程。在求解三维电磁问题的过程中,工作量主要体现在建立模型的过程。一旦模型建立完成,求解仅是计算机的计算过程,计算完成后返回画图界面是一个耗费时间的工作,并且无法针对无规律、不规则的结构问题进行反复计算或优化,而HFSS软件的宏命令则为上述想法提供了一个有效的解决方法[13]。
Ansoft公司开发的电磁仿真软件HFSS本身带有优化功能,可以利用软件的Optimistic模块选择需要优化的工程变量,然后根据设计意图进行优化设计。但是使用这种优化方法有一定的局限性,得到的最优值可能是局部最优而非全局最优,而且只能优化一个变量。HFSS使用VBS语言作为宏命令来进行二次开发,这为编写外部优化程序提供了可能。
本文使用HFSS-VBS建模语言,通过VBS脚本在HFSS软件中建立金丝连接微带线的模型,建模采用的是Rogers Duroid 5880基板,厚度为0.254 mm,相对介电常数2.2。微带线宽为0.76 mm,特性阻抗50 Ω。微带线间隙宽为0.2 mm,每段微带线长15 mm。键合线拱高设为150 μm。直径0.025 mm。
利用VBS中的循环语句修改参数使微带线的匹配半圆的半径由0.38 mm逐渐增加至1 mm,在循环语句内使用随机函数产生100组规定取值范围的8个随机数a,b,c,d,e,f,g,h作为两根金丝的4个落点的坐标值,即(x1,y1)、(x2,y2)、(x3,y3)、(x4,y4)4个落点。通过VBS脚本语言对大量模型进行上百次自动仿真,并将每一次产生的落点坐标和仿真结果的S参数提取至Excel,并使用Matlab进行数据处理。
3.2 仿真实现及优化
为了实现金丝与微带的匹配,在微带线不连续处金丝键合的两端分别加上一个半圆,如图6所示。增加了微带线宽度,从而增加了电容,以补偿金丝的电感。通过调节半圆的半径r来改变其特性阻抗,r从微带线宽度的一半0.38 mm开始取值,扫描范围为0.38~1 mm,在1~6 GHz进行频率扫描。
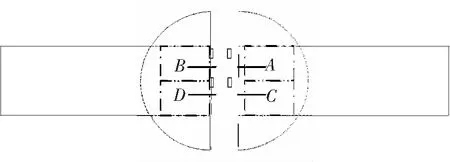
图6 微带线补偿示意图
用VBS脚本语言对仿真过程进行控制,在每一个半径取值处随机取一百种金丝的位置。通过统计人工打丝的落点坐标来确定随机落点的范围。首先把图6中A、B、C、D4个落点的坐标镜像到同一象限,分别计算其横坐标和纵坐标的统计参数,如表2所示。可以认为金丝落点的坐标分布服从正态分布,统计其数据进而计算出均值和方差。根据小概率原理,即概率很小的事件在一次试验中是几乎不可能发生的,和3δ准则,即随机变量服从正态分布时,其取值落在均值附近3δ区间之间的概率为0.997 4[14],可以认为工人在打丝操作中,其落点落在均值附近3δ之外的事件是一个小概率事件,几乎不可能发生。根据所得统计参数,计算出落点的3δ区间为x∈(0.02,0.374),y∈(0.155 5,0.323 5),进而确定在用HFSS进行仿真时选取落点范围为|x|∈(0,0.38),|y|∈(0.15,0.35)。

表2 键合线目标值与实测值对比
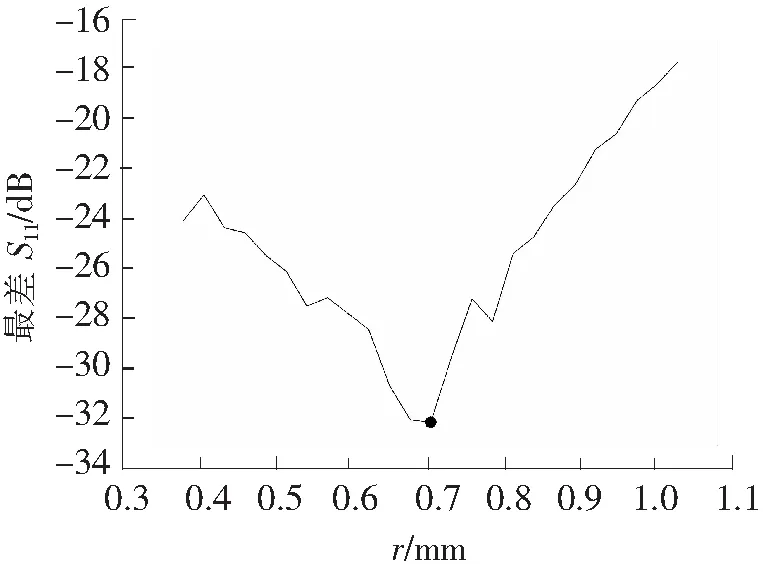
图7 不同匹配半径下的最差S11值
通过仿真优化并对仿真结果进行整理和统计,对应每一种半径的100种随机落点都会产生一簇S11参数曲线。在0.38~1 mm之间的24种半径取值下,找到24个S11曲线簇的最差点。比较这24个点的最差S11参数值,如图7所示。可以很直观地看出,在第12个取值处,即当半径为0.704 mm时,能够对键合线进行最好的补偿,传输线的传输性能最好。
4 测试及分析
4.1 测试平台
本次试验使用安捷伦公司的PNA-X矢量网络分析仪对加工的传输线试验板进行测试,频率范围为10 MHz~26.5 GHz。测试接头采用西南微波的Endlaunch接头,适用频率为0~18 GHz。
4.2 测试结果
针对仿真所得的最优匹配结论,加工了10套匹配后的传输线试验板如图8所示。对这10块试验板进行人工打丝,同样提前规定4个落点位置。加工完成后对两根金丝的4个落点进行测量,测量结果如图9所示。结果显示实际金丝落点均落在仿真过程中产生的随机落点范围内。最后,分别测试了1~6 GHz频率范围内的匹配前后S11参数,前后对比如表3所示。

图8 匹配后的传输线试验板示意图
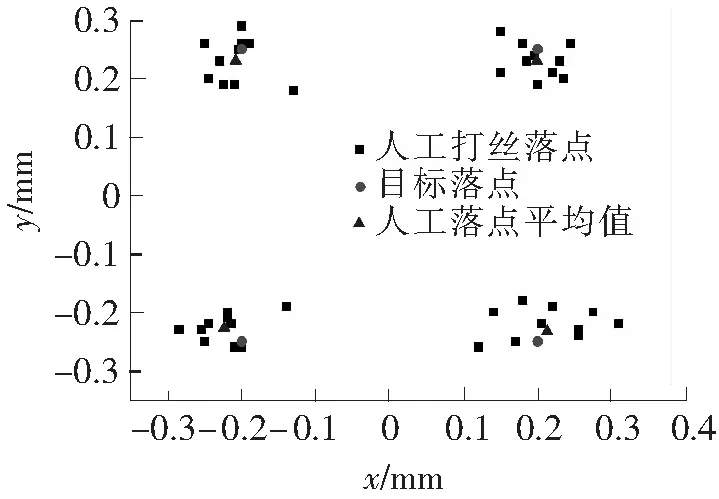
图9 匹配后金丝落点分布
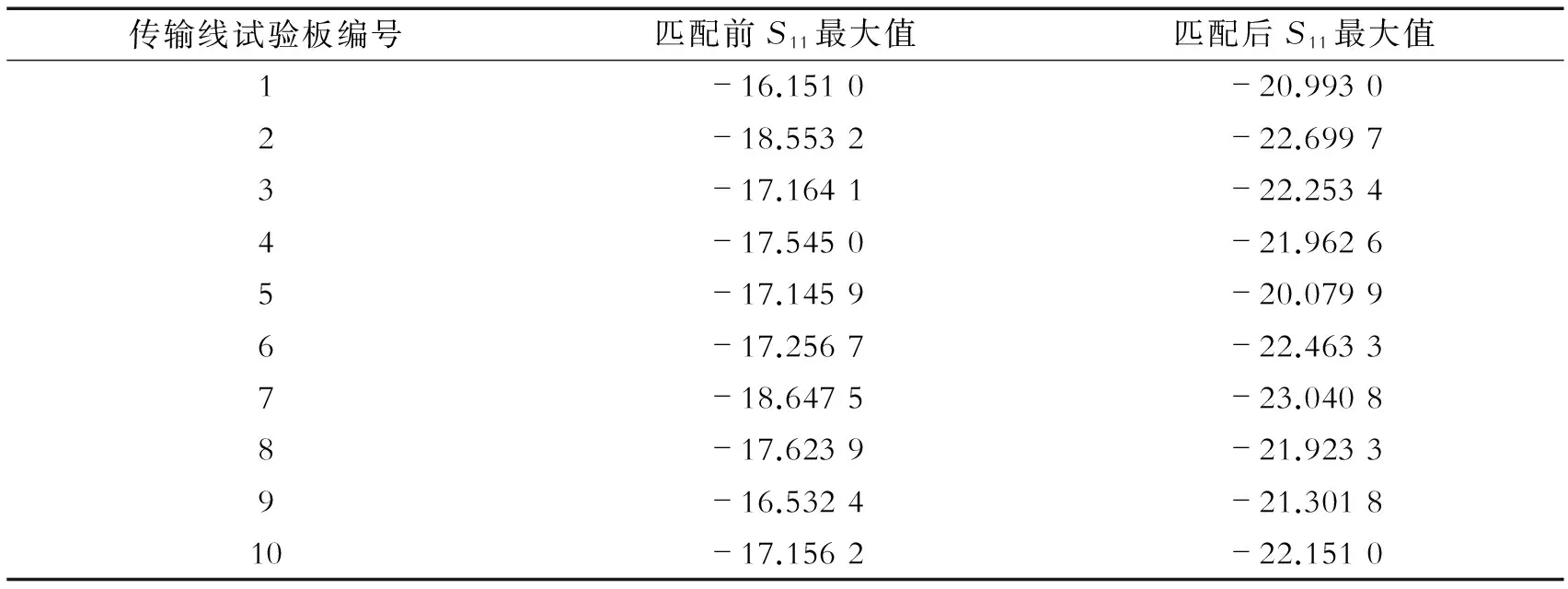
表3 匹配前后S11参数对比 dB
4.3 性能分析
如表3所示,在0~6 GHz范围内实现金丝的宽带匹配。匹配后的最大回波损耗相比匹配前的降低5 dB左右。由于设备条件所限,无法测量金丝的拱高,在进行建模仿真时只能大致估计。所以在较低频段对传输性能的改善不如仿真结果理想。
5 结论
本文介绍了一种对金丝键合进行补偿的新方法,基于蒙特卡洛仿真原理复现了人工打丝的不确定性。在不确定的前提下找到了一种最优匹配。使匹配更加符合实际情况,更加准确。该匹配方法可以应用在很多领域,比如电磁兼容。在后续工作中还可以继续完善相关参数进行仿真,如金丝拱高。使仿真模型更加准确,结论更加可靠。
[1]BAHL I. Lumped elements for RF and microwave circuits[M] . USA: Artech House, 2003: 146-155.
[2]段佐勇.微波功能模块微组装技术应用研究[D]. 南京:南京理工大学,2014.
[3]方勇. W波段防撞雷达集成前端关键技术研究 [D]. 成都:电子科技大学,2015.
[4]杨海峰, 邢孟江. 基于LTCC 技术的Ku波段金丝线匹配的研究 [J].电子元件与材料,2012, 31(5): 45-47.
[5]邹军, 谢昶. 多芯片组件中金丝金带键合互连的特性比较 [J]. 微波学报,2010(S1):378-380.
[6]张军,邓旭平,包龙生.响应面法在船撞桥可靠度分析中的应用[J].石家庄铁道大学学报:自然科学版, 2015,28(11):28-33.
[7]李鹏波. 战术导弹蒙特卡洛模拟及其可信性分析[J].战术导弹技术,1999(2):45-51.
[8]贾世旺,黄笑梅,张中海. EHF 频段键合线分析[J]. 无线电工程,2010,40(4):57-61.
[9]Alimenti F, Mezzanotte P, Roselli L, et al. An equivalent circuit for the double bonding wire interconnection [C]//IEEE MTT-S Digest.[S.l.]: IEEE, 1995.
[10]徐学军,李叶飞,冉彦详,等. 盲槽孔板的设计及加工方法探讨[J]. 印制电路信息,2010,10:415-421.
[11] 蔡童军,李金鸿,胡新星,等.一种特殊结构高频高速材料PCB加工问题探讨[J].印制电路信息,2012(S1):401-405.
[12] 王秉中.计算电磁学[M].北京:科学出版社,2012.
[13] 贾邦婕.基于粒子群算法的天线优化研究[D]. 昆明:云南大学,2015.
[14] 李孝轩,丁友石,严伟. 统计过程控制用于金丝键合质量控制研究[J]. 电子工艺技术,2009,30(6):346-348.

