基于控制点约束的地面三维激光扫描仪自检方法研究

,　　,　　,　

(1.天津大学 建筑工程学院，天津　300072；2. 天津市陆海测绘有限公司，天津　300191)

0　引言

地面三维激光扫描仪(以下简称扫描仪)近年来正呈现普及趋势，针对扫描仪的精度检测评估的国家或行业标准目前尚未制定颁布，因此对扫描仪自检方法的研究具有重要的意义。近年来一些学者进行了相关研究，并取得了一定的成果。文献[1-4]从测距、测角、温度环境影响等方面，提出具体的精度模型对扫描仪的精度进行测试和评定。冒爱泉等利用高精度基线场，通过基线比较计算扫描仪的加乘常数，给出误差修正模型[3]。张永彬等对扫描仪距离测量精度进行了试验研究，得出在一定距离内，测距精度相对较稳定，超出一定范围后随着距离的增加，内外符合精度逐渐下降[5]。张启福提出了基于人工标志的扫描仪自检校方法，并论证了该方法的可行性[6]。谢宏全根据六段解析模型对扫描仪测距精度进行了校验试验研究[7]。王瑞鹏等提出了基于球形靶标的加乘常数整体解算模型[8]。目前，国内外学者基本是在建立检校场的基础上，利用强制对中装置实现扫描仪扫描数据与其比较来评定扫描仪的精度，且大都只是检测评定其单一要素测量(例如测距)精度，但一般情况下扫描仪并不自带强制对中装置，其全要素(距离、水平角和竖直角)测量精度的同时检测评定是非常重要的[9-10]。以FARO公司的Focus3D X330扫描仪作为检测对象，利用仪器自带的对称基座和半球形标靶，以高精度的全站仪现场测设的控制点为约束，同时完成扫描仪的测距精度、测角(水平角和竖直角)精度的检测评估。该方法简单易实现，对制定扫描仪的精度检测评估行业标准具有一定的指导作用。

1　标靶球拟合的检测

1.1　标靶球拟合的检测方案

为了完整地扫描一个测区，一般需要对该测区进行多图幅的扫描，相邻图幅的相对定向和拼接必须依靠相邻图幅重叠区域内事先设置的一些公共标靶球来实现。扫描仪有自带的标靶球自动识别和球心坐标拟合算法的软件。标靶的拟合算法建立在扫描仪扫描到标靶球表面点云的数据特征上，数据量越多其拟合计算结果越可靠。而激光从扫描仪发出后呈发散状传播，距离扫描仪越远，激光的点间距就越大，落在标靶球上的点就会越少。如果扫描仪和标靶球之间距离过大，标靶球上的点云数据量过少，将影响扫描仪识别的精度，甚至不能识别标靶球。为此，本文设计在不同距离下标靶球被识别和拟合精度的试验，试验采用FARO公司的Focus3D X330扫描仪作为实验对象。检测试验标靶布置如下：选择两个高度相同、相距约3 m的固定点A、B，在这两点上放置直径为139.6 mm的标靶球，在这两点的中垂线上的25 m、30 m、40 m、50 m、60 m、70 m、80 m、90 m、100 m、110 m、120 m、130 m，140 m和150 m的地方(即图1中的1～14号点位处)分别架设三维激光扫描仪，分别用1/2倍的分辨率和1倍的分辨率对A、B这两个标靶球进行扫描，每站扫描10次。

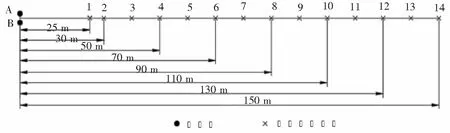
图1　标靶球拟合检测示意图

1.2　标靶球的拟合距离和识别精度

图2　标靶球拟合的距离D和中误差δ

将扫描仪的扫描结果数据导入到仪器自带的SCENE软件中，进行加载数据和查找球体操作，提取标靶球中心点的坐标(在距离较远处，软件无法自动识别时，采用手动识别)，能够拟合出的最远标靶的坐标如下：1/2倍分辨率下自动识别最远标靶坐标为(40.400，-0.014，-0.174)，手动识别为(70.234，-0.119，-0.104)；在1倍分辨率下自动识别最远标靶坐标为(70.154，-0.103，-0.154)，手动识别为(110.470，-0.143，-0.093)。为了尽量减小其他因素造成的误差，以两标靶之间的距离作为识别精度评定的标准。利用扫描仪拟合出的标靶球中心点坐标计算A、B两标靶球之间的距离，以10次的平均值为最或然值，求出中误差(见图2) 。

从图2可以看出，标靶球拟合的最远距离及识别精度与扫描仪自身的分辨率有很大关系：在1/2倍分辨率时，在40 m以内可以自动拟合，通过手动拟合最远距离为70 m，其误差在50 m以内不超过2 mm，50 m以外误差随距离逐渐增大；在1倍分辨率时，在70 m以内可以自动拟合，通过手动拟合最远距离为110 m，其误差在80 m以内不超过2 mm，80 m以外误差随距离逐渐增大。

2　扫描仪精度检测原理及方法

2.1　扫描仪测量误差解算原理

地面三维激光扫描仪由其内部的步进电机驱动仪器的上部和激光束转向镜分别绕竖直轴和水平轴旋转，仪器按照从上到下(逐行)、从右到左(逐列)的方向自动将激光依次投射到扫描范围内的被测物体上，经过被测物体表面的漫反射后被扫描仪接收到。这两个旋转轴的交点构成仪器坐标系的原点O，水平轴构成X轴，竖直轴构成Z轴，与X轴及Z轴垂直的为Y轴，O-XYZ构成右手坐标系。在扫描仪的实测数据中，仪器首先测量出坐标原点至被测物体之间的距离s、水平角θ、竖直角φ，然后将测量值(s,θ,φ)转换成仪器坐标系中被测点的三维直角坐标值x、y、z

[x,y,z]T=[scosθcosφ,ssinθcosφ,ssinφ]T

(1)

对式(1)进行全微分可得

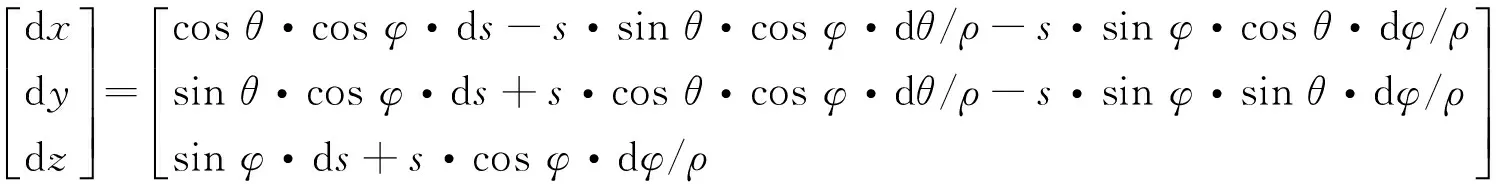
(2)

其中ρ=180°×3 600″/π=206 265″。当水平角θ=90°、竖直角φ=0°时，将式(2)变换后可得

[ds,dθ,dφ]T=[dy,-ρdx/s,ρdz/s]T

(3)

由式(3)可以得知，在检测扫描仪时，首先在检测现场沿扫描仪坐标系的Y轴方向设置若干与扫描仪大致等高的控制点(即基本保证：水平角θ=90°，竖直角φ=0°)，通过其他方法精确测得这些控制点的三维直角坐标，然后与扫描仪测得的三维直角坐标进行比较，求得扫描仪所测控制点坐标的误差(dx, dy, dz)，再由式(3)分别求得扫描仪的测距误差ds、水平角测量误差dθ和竖直角测量误差dφ(式(3)中的s由直角坐标反算求出)。

2.2　基于控制点约束的扫描仪检测方法

2.2.1对称基座与半球形标靶

在采用高精度全站仪现场测设控制点时，为了统一全站仪和扫描仪两者的仪器坐标系和对控制点同一部位的测量，必需借用如下扫描仪自带的辅助设备：

(1)对称基座。如图3(a)所示，以扫描仪中心为对称点的左右各一个对称基座，在基座上安置反射棱镜，全站仪通过测量两对称基座上反射棱镜的坐标，从而求得扫描仪中心的坐标。

(2)半球形标靶。如图3(b)所示，半球形中部嵌入一个反射棱镜，棱镜中心与球心重合，便于扫描仪和全站仪的同时瞄准测量，两仪器所测的结果均为控制点同一部位的坐标值。

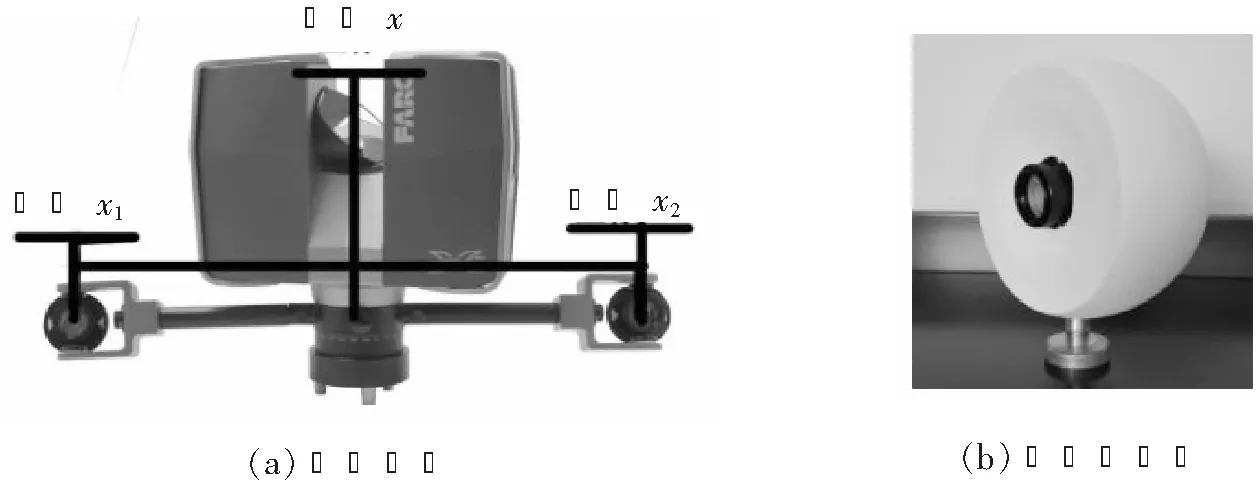
图3　对称基座与半球形标靶

2.2.2检测控制场的建立与检测步骤

采用Leica TC1201高精度全站仪进行检测，其测距精度为(1 mm+1.5×10-6)，测角精度为1″。检测控制场如图4所示，全站仪距离扫描仪约10 m，在全站仪与扫描仪连线的延长线上，且距离扫描仪分别为5 m、10 m、15 m、20 m、25 m、30 m、40 m、50 m、60 m、70 m、80 m、90 m、100 m、150 m、200 m、250 m、300 m的地方安置半球形标靶作为待测标靶。在离扫描仪25 m且偏离延长线10 m处安置一半球形标靶作为定向标靶，用于全站仪和扫描仪统一的后视方向。扫描仪采用1倍分辨率进行扫描，当距离超过110 m后，由于标靶球不能被扫描仪拟合，故采用中心带有反射片的平面标靶作为待测标靶，分别将平面标靶安置在150 m、200 m、250 m、300 m位置处。

图4　检测控制场示意图(单位：m)

检测步骤：(1)安置全站仪、扫描仪、定向标靶，在距离扫描仪5 m处安置待测标靶；(2)根据全站仪初测后调整待测标靶高度，使其中心尽量和扫描仪保持等高；(3)用全站仪测得扫描仪左右两对称基座上反射棱镜的坐标、定向标靶的坐标和待测标靶的坐标；(4)用扫描仪对待测标靶和定向标靶分别扫描10次；(5)将待测标靶摆放在距离扫描仪10 m处，重复以上(2)、(3)、(4)操作步骤，再将待测标靶摆放在距离扫描仪15 m处，直到完成所有位置处待测标靶的测量和扫描。

2.2.3待测标靶的坐标提取

根据全站仪的数据，计算出扫描仪中心的坐标，再将扫描中心坐标和定向标靶中心的坐标导入SNECE软件中，从而实现扫描仪和全站仪坐标系的统一。然后将所有扫描数据导入SNECE软件中，依次提取出不同位置处待测标靶中心点的坐标，并计算各待测标靶坐标的平均值(对于距离超过100 m的平面标靶中心，由于SNECE软件不能自动识别，故通过其点云手动识别)。

3　扫描仪测量误差分析

将扫描仪对各标靶10次扫描所得坐标分别与各标靶坐标平均值(最或然值)比较、与全站仪测得的各标靶坐标(真值)比较，可以算得扫描仪所测各标靶三维坐标的内符合误差(dx′,dy′,dz′)和外符合误差(dx, dy, dz)，然后根据式(3)求得扫描仪对各标靶的距离s、水平角θ和竖直角φ测量的内、外符合误差，进而求出内、外符合中误差，计算结果如表1。

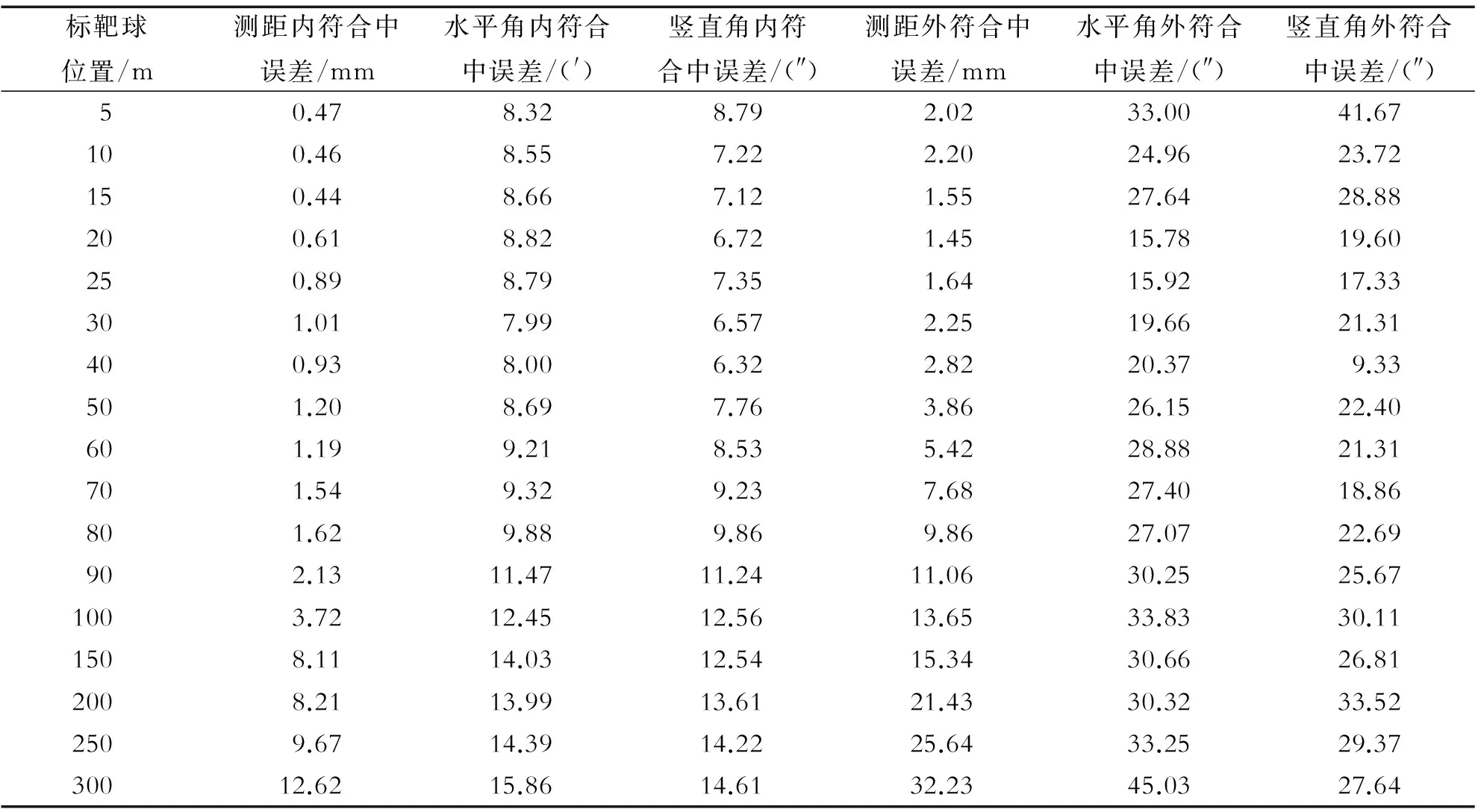
表1　三维扫描仪测距测角误差

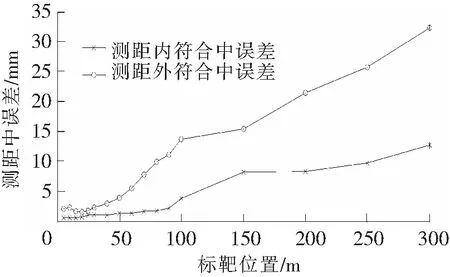
图5　扫描仪测距中误差

3.1　测距误差分析

扫描仪测距中误差结果见图5。

扫描仪测距的内符合中误差在90 m以内不超过2.13 mm，在300 m时达到12.62 mm；扫描仪测距的外符合中误差在40 m以内不超过2.82 mm，在300 m时达到32.23 mm，且在25 m以外时与标靶球的距离存在很明显的线性相关。由于扫描仪的测距原理属于光电测距范畴，其外符合误差模型可以采用加乘常数模型，根据多段基线扫描结果列出误差方程[1]

δ=(S0-S)-K-R·S

(4)

式中，K为加常数；R为乘常数；S0为基线参考值(即全站仪测出的扫描仪与待测标靶的距离)；S为扫描仪测得的标靶的距离；δ为误差改正数。为了降低标靶拟合精度对实验结果的影响，该文将80 m以内的实测标靶数据代入误差方程，根据间接平差原理，解算出该扫描仪的加乘常数分别为：K=2.75 mm，R=7.64×10-5。

3.2　测角误差分析

从表1、图6和图7可以看出：

(1)扫描仪水平角和竖直角测量的内符合中误差在80 m以内分别不超过9.88″和9.86″，在300 m时分别达到15.86″和14.61″；内符合中误差的曲线基本都很平缓，与标靶球的距离不存在较强的相关性(其随距离有所增大的原因可能是由于折光误差引起的测角误差)。

(2)扫描仪水平角和竖直角测量的外符合中误差变化范围分别为15.78″～45.03″和9.33″～41.67″，且其最小值与最大值并非发生在最小距离和最大距离处；它们的曲线均为上下波动状，与标靶球的距离不存在明显的相关性；水平角和竖直角测量的外符合中误差的平均值(即各中误差之和取平均)分别为27.66″和24.72″，均小于其标称分辨率32.4″。

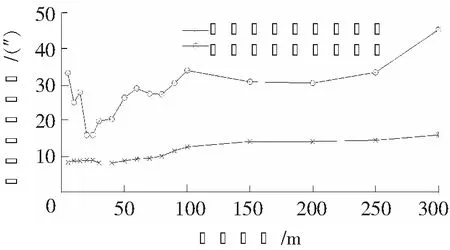
图6　扫描仪水平角测量中误差

图7　扫描仪竖直角测量中误差

4　结论

以FARO公司的Focus3D X330地面三维激光扫描仪作为检测对象，对其标靶球拟合的最远距离及识别精度、距离测量精度、水平角测量精度和竖直角测量精度进行了检测，得到了以下几点结论：

(1)标靶球拟合的最远距离及识别精度与扫描仪自身的分辨率有很大关系，在1倍分辨率时，自动拟合和手动拟合的最远距离分别为70 m和110 m，其拟合误差在80 m以内不超过2 mm。

(2)扫描仪测距的外符合中误差在25 m以外时与标靶球的距离存在很明显的线性相关，在40 m时中误差为2.82 mm，在300 m时达到32.23 mm。扫描仪测距的外符合误差模型可以采用加乘常数模型，通过解算得其加乘常数分别为：K=2.75 mm，R=7.64×10-5。

(3)扫描仪水平角和竖直角测量的外符合中误差变化范围分别为15.78″～45.03″和9.33″～41.67″，与标靶球的距离不存在明显的相关性。水平角和竖直角测量的外符合中误差的平均值分别为27.66″和24.72″，均小于其标称分辨率32.4″。

(4)利用扫描仪自带的对称基座和半球形标靶，以高精度的全站仪现场测设的控制点为约束，同时完成了扫描仪的测距精度和测角精度的检测评估，此方法简而易行，对于未来地面三维激光扫描仪精度检测评估行业标准的制定具有一定的指导意义。

[1]刘春. 地面三维激光扫描仪的校准和精度评估[J]. 测绘通报, 2013(12): 25-27.

[2]Lichti D D, Licht M G. Experiences with terrestrial laser scanner modeling and accuracy assessment [C]// Proceedings of the ISPRS Commission V Symposium: Image Engineering and Vision Metrology: XXXVI. Dresden: ISPRS, 2006: 155-160.

[3]冒爱泉, 朱益虎, 郝思宝, 等. 地面三维激光扫描仪精度测评方法和误差改正模型研究[J]. 测绘通报, 2014(2): 72-75.

[4]郑德华, 沈云中, 刘春. 三维激光扫描仪及其测量误差影响因素分析[J]. 测绘工程, 2005, 14(2): 32-34.

[5]张永彬, 高祥伟, 谢宏全, 等. 地面三维激光扫描仪距离测量精度试验研究[J]. 测绘通报, 2014(12): 16-19.

[6]张启福, 孙现申, 李宗春. 基于人工标志的三维激光扫描仪自检校方法研究[J]. 测绘通报, 2012(S0): 80-84.

[7]谢宏全, 高祥伟, 邵洋. 地面三维激光扫描仪测距精度检校试验研究[J]. 测绘通报, 2013(12): 25-27.

[8]王瑞鹏,王力,李广云,等. 基于球形靶标的三维激光扫描仪加乘常数测定方法[J].测绘通报，2014(S1):133-134.

[9]郑岗,戴玮,谢玉萌. 三维钢筋建模统计及自动出样方法研究[J]. 石家庄铁道大学学报：自然科学版,2015,28(4):34-38.

[10]王军文,王罡,张运波. 钢管混凝土连续梁拱组合桥施工期拱脚应力监测与分析[J]. 石家庄铁道大学学报：自然科学版,2015,28(4):1-5,21.