体验数据随机性，培养数据分析观念——以“掷一掷”为例

□斯 瑶

随着对“统计与概率”领域的探索与教学，我们意识到教学绝非停留在绘制统计图、求平均数等知识技能的传授上，数据分析观念的建立，更符合学生发展的需求。“数据分析观念”成为《义务教育数学课程标准（2011年版）》所提出的十大核心概念之一，也是“统计与概率”领域的核心。史宁中教授对“数据分析观念”的内涵进行了阐述，认为“体验数据的随机性”是数据分析观念的一部分，它有两个层次的含义：一是对于同样的事情每次收集到的数据可能会是不同的，二是只要有足够的数据就可能从中发现规律。

那么，在小学数学的教学中如何体现数据分析观念，如何让学生体验数据的随机性？本文将以人教版五年级上册“掷一掷”一课为例，结合教学实践，谈谈笔者的想法。

一、着眼解决问题，体会收集数据的必要性

数据分析观念的培养需要基于学生感兴趣的事物，进而引导学生了解要解决现实问题往往需要经历调查、数据收集、分析的过程，并根据数据中蕴含的信息进行推断。创设解决问题的现实背景，能有效沟通数学知识与具体问题间的联系，激发学生主动参与探究活动的积极性。因此在了解了掷两枚骰子面朝上的点数和可能是2～12这11种可能之后，创设了古代小商贩摆赌局的情境。玩家掷一次付给商贩10文钱，如果掷出的点数和是2，3，4，9，10，11，12这7个数，则商贩付给玩家20文钱，反之则10文钱归商贩。点数和7∶4的分组设计区别于教材中6∶5的分组设计（2，3，4，10，11，12为一组，5，6，7，8，9为一组），其原因在下文中会谈到。

学生在学习本课之前，已经在“可能性”单元通过简单试验体会可能性是有大小的，并与数量的多少有关。表决统计也显示，全班44人，有40位同学表示玩家赢的可能性大，理由是数量点数和多。3位同学表示玩家赢的可能性小，理由分别是：商贩以营利为目的，不会输；每个点数和的组合不同，只有掷出1和1才能出现点数和2。有1位同学表示可能性一样大，综合了两方的想法。此时，即便是觉得玩家输的可能性大的3位同学也是出于一种感觉。当即教师提出问题：怎样才能知道玩家究竟是赢的可能性大还是输的可能性大。学生立即反应，做实验，并不断有学生补充，需要大量做实验，对实验结果还需要进行记录统计以发现规律。

培养数据分析观念，首先就要让学生经历产生统计思想的过程，体会统计在解决问题中的必要性。实验、统计、发现规律，在教师的引导过程中，学生逐步构建数据分析的过程，数据分析观念也慢慢在学生脑中形成。

二、实验统计，体验数据的随机性

对于同样的事件，每次收集到的数据可能会不同，而大量收集数据后有可能会形成某种规律。这就是数据的随机性。从部分推断整体是统计的一个基本思想，既然是由部分来推断，我们就不能保证推断是准确无误的。这也是产生数据随机性的原因之一。

在“掷一掷”一课的教学中，学生自主提出通过实验和统计探究玩家输赢的可能性大小。随即开展了四人小组合作的实验活动。教师提供了类似条形统计图的表格，掷出的和是多少就在对应的点数和上方涂一格，任意一列涂满，游戏结束。

这里就要谈到7∶4分组的设计意图。两枚骰子点数的组合方式共36种，6∶5的分组设计，点数和出现的可能性大小分别是和。7∶4的分组设计，点数和出现的可能性大小分别是和。细小的变化，却让实验结果变得更为有趣。全班共分成11个小组，下图为3个小组的实验结果。

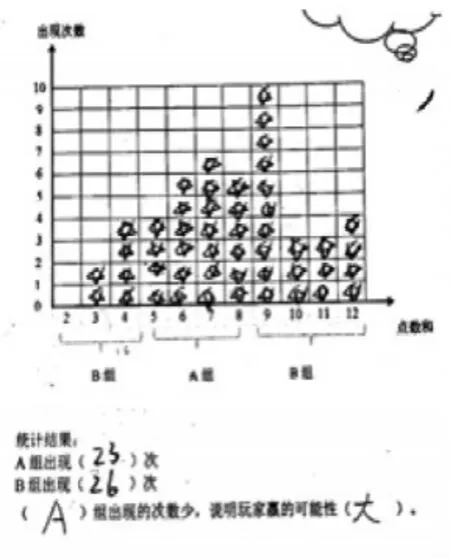
图1

图2

图3

由于两组数出现的概率较接近，学生的实验结果中，两组数掷出的次数也会相对较接近。即便如此，全班11个小组，每个小组最终掷的次数都在50次左右，其中10个小组都得到了玩家赢的可能性小的结论。通过观察统计图，学生都发现中间的点数和出现的次数多一些，两边的少一些。这里，也让学生些许体会到统计与概率的魅力。但在反馈图1和图2后，学生也感受到两组数据统计结果的差异，初步体会数据的随机性。在几次试教中，几乎每个班都会出现有一组是玩家胜利的结果，如图3。这就让课堂变得更为有趣。学生的回答也非常精彩：我们小组的统计图也呈现中间多两边少的形状，但由于9出现的次数异常多，所以我们组得到的结论是A组出现次数少，玩家赢的可能性大。至此，学生对数据的随机性又得到了更深刻的体验。

由部分推断整体，然而部分数据存在随机性，因而结论也会出现偏差。

三、归纳推理，感悟数据的规律性

统计是用数据进行推断，其推理方式主要是归纳。而实际教学中，教师往往习惯于先给出定义。以“抛硬币”为例，一般的教学步骤是：①面朝上的可能有哪些？（可能是正面朝上，也可能反面，基于概率角度的随机性）②它们的可能性大小是多少？（几乎每个五年级的孩子都知道正面或反面朝上的概率是二分之一）③学生或计算机实验验证。这就类似于演绎推理的过程，先得出结论再进行实验，而学生对于数据随机性的体会是模糊而不深刻的，更谈不上数据分析观念的建立了。

在前文的论述中，已经阐述了学生通过实验体验了数据的随机性。而数据随机性中，还包括了一点，只要有足够的数据，就可以从中发现规律。在这里笔者将它称为数据的规律性。

学生在感知数据具有随机性，小数据更具有偶然性后，开始主动寻求大数据，探究规律。有学生想到将全班的数据合在一起。课前安排了大组的观察员，在小组合作实验结束后，统计了大组的实验数据。课堂上将各个大组的数据通过excel统计形成统计图，在输入的过程中，引导学生不断发现规律：随着数据的增加，统计图“山”一样的形状越来越稳定。从而帮助学生体会到收集大量的数据后就会形成某种规律，让学生对数据的随机性也有了更完整的认识。

已有经验与实验结果的冲突，让学生不禁质疑：明明占的点数和少，为什么出现的次数反而多呢？为什么会呈现中间多两边少的形态？进而激发学生继续探究的欲望，引起学生思考。在实验过程中，会有学生感悟到每个点数和出现的可能性大小不同，这与数的组成有关。

从实验到统计，从统计到数据分析，揭秘真相，这样一个类似于“猜谜”的活动，学生既体会到了数据的随机性，又感受到数据中蕴含着信息，大数据中还可能蕴藏规律，帮助我们作出判断。这实际就是一个归纳推理的过程。在小学阶段，教材上有让学生经历归纳推理的过程，但大多都是规律、公式、定理的推导。像这样通过自己创造的数据推理现实问题，从部分数据推断整体结果的具有统计意义的推理，于学生而言是非常难得的。

四、理论实践相结合，感受数据统计的魅力

在学生谈到点数和出现的可能性大小与数的组成有关后，笔者让学生在表格中记录所有点数和是2～12的算式，如图4，再次观察，看看有什么发现？

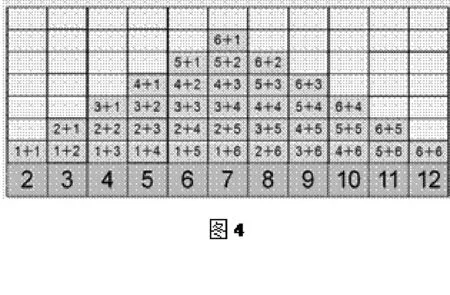
图4

通过观察进而发现，出现点数和5，6，7，8的可能为20种，所以出现的可能性大，剩余7个点数和出现的可能有16种，出现的可能性小。学生也体会到，可能性的大小不能由表面的数量决定，要找到真正影响可能性大小的因素。在这个游戏中影响可能性大小的因素是数的组合方式。

从数据分析到探究原因，从实践操作到理论分析，是学生自己得到的实验数据推动着进一步的思考，是主动的探索与发现。

课堂最后，笔者将通过实践得到的统计图（图5）和通过数的组成分析得到的表格（图4）进行对比，两幅形似“山”一样的图片重合在了一起，让笔者产生视觉的冲击，同时也让学生说说自己的想法。一学生回答道：实践与理论是一致的。学生都不禁感叹，两幅图惊人的相似。

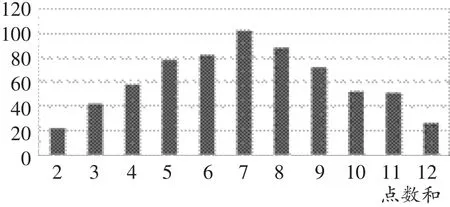
图5

“点数和”出现次数统计图出现次数

这一环节的设计，旨在帮助学生感悟任何不确定事件的背后一定有理可依，偶然中藏着某种必然。这是学习数学的价值，它可以在一定程度上帮助我们分析生活中的不确定事件。这同样也是统计的魅力所在，通过数据统计可以帮助我们对实物作出判断。就像我们常说的，理论指导实践，实践检验真理。

要让学生建立起数据分析观念，需要让学生在解决问题的过程中，亲身经历统计思想产生和发展的过程。在体会数据分析的必要性后，通过实验统计分析数据，感知可以通过部分推断整体，即便这个“部分”存在一定的随机性。以归纳推理的形式，展开数据分析，对于帮助学生建立数据分析观念，渗透统计思想，具有重要意义。

参考文献：

[1]史宁中，张丹，赵迪.“数据分析观念”的内涵及教学建议[J].课程·教材·教法，2008（6）:40-44.