基于演化博弈的台风灾害应急疏散决策机制研究

，　 ，　

(哈尔滨工程大学 经济管理学院，黑龙江 哈尔滨 150001)

1　引言

近年来，世界各地不断受到台风侵袭，2012年的“Sandy”飓风袭击了美国，约30万人口从沿海低海拔区域疏散到内陆较高海拔区域[1]。而我国作为遭受台风影响严重国家，仅2016年就受到29次台风影响，约70万人口进行了紧急疏散。当台风灾害即将来临时，危险地区的人群通常会依据个体主观判断做出撤离的决策，然而考虑到撤离成本、家庭财产以及不可预知的其他风险，一部分被疏散者会采取冒险的滞留策略[2]，给自身、家庭乃至国家带来一定的消极影响。可预知自然灾害的疏散、撤离、妥善安置受到威胁的人员以及采取其他救助措施，是我国政府应急管理的重要内容之一。因此，探究台风灾害影响下被疏散群体的撤离行为决策及意志导向，对完善我国应急疏散预案、促进应急管理发展具有重大的实践意义。

国外关于飓风疏散的相关研究表明：人们更愿意以家庭为单位，接受疏散指令决定是否撤离，撤离决定主要基于指令的类型(自愿疏散或政府参与的强制疏散)、对疏散指令的信任度、对风险的感知度、对疏散方案的经验认可度等[3,4]。对于疏散决策的研究，多集中于疏散需求领域，通过疏散与否，疏散时间和路径的综合研究对交通需求进行预测[5～7]。而是否参与疏散则从个体角度出发，通过利用调查的数据构建Logistic回归模型判断影响决策的因素[8,9]，及人工神经网络模型等预测交通需求[10]。其中Fu[11]通过序贯的Logit模型将疏散过程分成多时段分析被疏散者的撤离策略选择；Hasan等[12]介绍了风险建模方法中的随机参数以理解家庭层级的疏散决策；Gudishala和Wilmot[8]构建了二元Logistic模型分析被疏散群体选择不撤离策略的影响因素。

国内已有关于疏散的研究多集中于大型建筑物、集散地等范围的微观个体疏散层面[13,14]，针对台风灾害下大规模区域应急疏散的研究相对较少。其中高明霞对城市道路交通应急疏散问题做了相关探讨[15]；安实等[16]针对台风灾害重点研究了关于疏散的交通需求预测问题；吴文祥和黄海军[17]发现通过发布最优信息，可以缓解交通拥挤，实现交通系统最优状态；吴健宏等[18]基于地理信息系统利用仿真平台研究城市应急疏散中信息发布对疏散结果的影响。此外，学者们多从缓解交通拥堵现象的视角基于演化博弈理论，对疏散、出行等问题进行相关研究[19,20]。Han等[21]利用博弈思想建立了个体出行的决策模型；肖海燕和王先甲[22]运用演化博弈理论对政府参与条件下的出行方式选择行为进行了分析；周勇等[23]根据疏散资源的稀缺性和疏散资源使用者的自私性等结合博弈论模型提出了缓解拥堵问题的对策。

通过文献梳理发现，国内外学者对于应急疏散决策的研究已经取得了较为丰富的成果，相关研究多集中于利用行为决策理论，预测疏散过程中的交通需求。然而，针对利益博弈关系的应急疏散研究相对较少，且对政府参与条件下被疏散者决策变化的研究更为匮乏。基于此，本文利用演化博弈理论对台风灾害下撤离疏散的决策机制进行研究，打开被疏散群体撤离决策行为的“黑箱”，从被疏散者对于疏散资源竞争的视角对驱动其决策的利益博弈关系进行深入剖析，从而理解被疏散的目标人群所做出的撤离行为决策的依据。同时，本文分别分析了自愿撤离和政府参与条件下的均衡状态，突出了政府参与疏散行动的重要作用，为政府制定相关的政策提供有益借鉴。

2　基本假设

根据Gladwin等[24]的研究，基于微观视角分析，虽然政府会发布疏散指令(自愿或强制)，但最终决定权仍然掌握在危险地区的被疏散群体中，政策制定者不能期望所有群众完全听从指令。因此，根据研究需要选择被疏散群体作为研究对象具有实际意义。被疏散群体在接到台风预警后，选择是否撤离是一个决策问题，与被疏散群体的决策心理以及被疏散成员之间的相互影响有关。在台风灾害影响下，被疏散群体为保护其生命财产安全的同时使其成本最小收益最大做出是否疏散的决策。但由于社会资源总量有限，选择撤离的人群比例越高，则撤离的成本越高，进而干扰决策。因此，被疏散者在选择是否撤离和其他被疏散者选择撤离策略之间存在博弈关系。在有限理性条件下，被疏散群体在收到台风预警后会继续收集相关信息辅助决策，在开始阶段被疏散者依据自身经验会有策略选择偏好，将其划分为选择撤离策略的被疏散群体和选择不撤离策略的被疏散群体，被疏散者根据对台风灾害的风险估计，撤离所能保护的生命财产安全，撤离所舍弃的资产以及撤离成本之间的权衡，选择收益最大的策略。经过一段时间演化，群体成员间随机配对、相互学习、重复博弈使个体得到收益最大化的策略，其策略调整过程可以用复制动态机制来模拟，最终导致群体意义上的策略均衡。当系统呈现均衡状态时，可以得到被疏散群体选择特定策略的比例，为制定有效的管理策略影响系统中的被疏散者的撤离策略提供理论依据，使撤离人群比例朝着管理者期望方向演化。基于Han等[21]，Gladwin等[24]和安实等[16]的研究，本文提出如下假设：

假设1在某即将可能受台风灾害影响的地区，被疏散群体需要争夺某些社会资源(如公路道路资源，油气资源，应急设施资源等)以保证自己利益最大化，根据被疏散群体的选择偏好将该地区人群划分为两类有差别的有限理性群体，即被疏散群体1和被疏散群体2，其中被疏散群体1为撤离策略偏好型，被疏散群体2为不撤离策略偏好型，两类群体均处于台风威胁环境下(台风预警)。

假设2被疏散群体1和被疏散群体2在灾害条件下收到气象部门发布的台风预警消息后，假设灾害实际发生的概率为α，群体中的决策者均有两种策略选择，即撤离危险地区和停留在危险地区，策略集为{撤离，不撤离}。

假设3被疏散群体i所拥有的总资产为Pi，包括物质财产和生命财产等。为了保证生命财产安全，被疏散者选择撤离策略时，会舍弃部分固定资产Ci，离开家到避难点等其他安全地点，同时撤离过程需要消耗如时间、路费、外宿等成本Di，因此双方都选择撤离策略的收益为Pi-αCi-Di。

假设4当被疏散群体对α的估计值偏低时，往往选择不撤离策略，收益为(1-α)Pi。而一方在选择不撤离策略时，会让出社会资源给撤离的群体，减少撤离过程中的道路拥堵，导致撤离的成本降低，设减少的撤离成本比率为β，则撤离过程的成本为(1-β)Di。

3　自愿撤离条件下的决策机制分析

3.1　模型构建

根据以上假设，收到台风预警后，自愿撤离条件下，被疏散群体1和被疏散群体2作为决策主体在选择撤离和不撤离两种策略下的博弈收益矩阵如表1所示。

表1　自愿撤离条件下被疏散群体的博弈支付矩阵

假设在博弈初始阶段，被疏散群体1中采取撤离策略的比例为x，采取不撤离策略的比例为(1-x)；被疏散群体2中采取撤离策略的比例为y，采取不撤离策略的比例为(1-y)。x、y的值随着时间t的变化而变动，由表1可得：

被疏散群体1选择撤离策略E的收益为

UE1=y(P1-αC1-D1)+(1-y)·

[P1-αC1-(1-β)D1]

(1)

被疏散群体1选择不撤离策略S的收益为

US1=y[(1-α)P1]+(1-y)[(1-α)P1]

(2)

被疏散群体1采取撤离策略E和不撤离策略S的期望收益为

U1=xUE1+(1-x)US1

(3)

被疏散群体2选择撤离策略E的收益为

UE2=x(P2-αC2-D2)+(1-x)·

[P2-αC2-(1-β)D2]

(4)

被疏散群体2选择不撤离策略S的收益为

US2=x[(1-α)P2]+(1-x)[(1-α)P2]

(5)

被疏散群体2采取撤离策略E和不撤离策略S的期望收益为

U2=yUE2+(1-y)US2

(6)

被疏散者根据多次博弈结果来调整对策略的选择，被疏散群体的撤离策略的演化可以用如下的复制动态微分方程来表示

f(x)=dx/dt

=x(1-x)[-βD1y+αP1-αC1-(1-β)D1]

(7)

f(y)=dy/dt

=y(1-y)[-βD2x+αP2-αC2-(1-β)D2]

(8)

3.2　稳定性分析

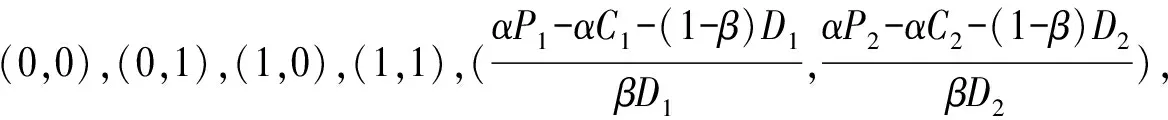
(9)

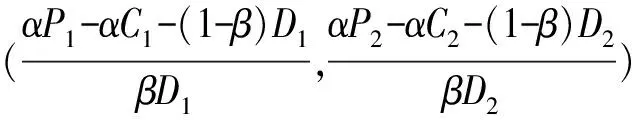
(10)

则矩阵J0行列式为[αP1-αC1-(1-β)D1]·[αP2-αC2-(1-β)D2]，矩阵J0的迹为αP1-αC1-(1-β)D1+αP2-αC2-(1-β)D2。当矩阵的行列式为正值且迹为负值时，(0,0)是被疏散群体撤离决策演化博弈的稳定点。同理，分析4个均衡点的稳定性可以得到以下结论：

结论1αP1-αC1-(1-β)D1>0且αP2-αC2-D2<0时，(1,0)是系统的演化稳定点，经过变换可得到α(P1-C1)>(1-β)D1且α(P2-C2)0且αP2-αC2-D2<0的条件下，虽然被疏散群体1和群体2均选择撤离策略，但群体2中的个体由于撤离并没有收益，反而会有损失，则会放弃撤离，为群体1的人让出社会资源。

结论2αP1-αC1-D1<0且αP2-αC2-(1-β)D2>0时，(0,1)是系统的演化稳定点，即α(P1-C1)(1-β)D2，说明被疏散群体1采取撤离策略而保障的生命财产安全小于撤离过程的成本，而被疏散群体2采取撤离策略的收益大于在部分撤离条件下的撤离成本，经过多次博弈后，系统达到被疏散群体1的个体全部选择不撤离策略，被疏散群体2的个体全部选择撤离策略的稳定状态。例如，对于老年人和残疾人等特殊群体，撤离过程中的成本过高时，即使台风来临的风险值很高，仍会采取冒险策略，选择不撤离策略。

结论3当αP1-αC1-(1-β)D1<0且αP2-αC2-(1-β)D2<0时，(0,0)是系统的演化稳定点，即α(P1-C1)<(1-β)D1且α(P2-C2)<(1-β)D2，说明在台风预警条件下台风来临的情境撤离行动可以获得的收益小于撤离过程中所消耗的成本。也就是当撤离的效用并不明显时，那么被疏散者都会选择留在家中。这种情况通常发生于被疏散群体对于α的估计值较低，双方经过多次博弈均对于此次台风的风险感知水平较低，即使都放弃撤离，撤离成本降低，但仍然会在多次博弈后选择不撤离，放弃撤离策略。

结论4αP1-αC1-D1>0且αP2-αC2-D2>0时，(1,1)是系统的演化稳定点，即α(P1-C1)>D1且α(P2-C2)>D2，说明被疏散群体1和被疏散群体2在都采取撤离策略时，能够保障的生命财产安全的效用均大于在撤离过程中消耗的成本，则即使所有群体均采取撤离行动，即使撤离成本较高，仍小于撤离行动所带来的财产安全的保证。因此，在这种条件下，长时间博弈后，两个群体中的被疏散者均会选择撤离策略，系统达到稳定状态。

4　政府参与疏散条件下的撤离决策机制分析

4.1　模型构建

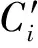
表2　政府参与条件下被疏散群体的博弈支付矩阵

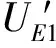
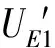
(11)

政府参与下被疏散群体1选择不撤离策略S的收益为

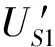
(12)

政府参与下被疏散群体2选择撤离策略E的收益为

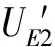
(13)

政府参与下被疏散群体2选择不撤离策略S的收益为

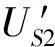
(14)

因此，政府参与疏散指令条件下，被疏散群体的撤离决策演化可以用如下的复制动态微分方程来表示

g(x)=dx/dt

=x(1-x)[-β(1-δ)D1y+γP1-

(15)

g(y)=dy/dt

=y(1-y)[-β(1-δ)D2x+γP2-

(16)

4.2　稳定性分析

相似地，令(15)、(16)式微分方程中的g(x*)=g(y*)=0，得到5个局部稳定点，分别是(0,0)，(0,1)，(1,0)，(1,1)和

(17)

将均衡点分别带入雅克比矩阵，根据其行列式和迹的符号，判断演化系统在均衡点的稳定性，可以得到以下结论：

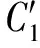
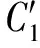
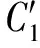
5　结论与启示

本文基于应急疏散决策理论，利用演化博弈方法从自愿撤离和政府参与两方面分析了台风灾害影响下被疏散群体撤离行为的决策机制。结果表明：

(1)在自愿撤离条件下，当得到台风预警后如果台风发生并且采取了撤离的策略，能够挽救的生命和物质财产收益小于当部分被疏散群体选择不撤离策略时的疏散过程消耗的成本时，双方最终都会选择不撤离。相反，当被疏散群体采取撤离策略可能挽救的生命和物质财产大于全体撤离时所消耗的撤离成本，双方才会全部选择撤离策略。而当一方选择不撤离时，所让出的疏散资源保证另一方撤离成本小于其保障的财产时，另一方选择撤离。

(2)被疏散群体的总资产、固定资产、对台风来临的概率估计、疏散过程的成本和当疏散人数减少所导致的疏散成本降低比率对被疏散群体的决策结果都有显著的影响。其中被疏散群体的总资产量，对台风来临概率的估计以及一方不撤离减少疏散成本比率的增加对于被疏散群体选择撤离策略有正向促进作用。说明当撤离行动能够带来的安全保证大于其损失的风险，则被疏散群体倾向于撤离策略。被疏散群体的固定资产量和撤离成本的增加会对被疏散群体选择撤离策略有反向促进作用。表明阻碍人们选择撤离策略的原因一方面在于想要保护其固定资产，另一方面则出于对疏散过程的拥堵可能带来其他风险以及损失的考虑。

(3)政府参与疏散对被疏散群体选择撤离策略有促进的作用，这里体现在政府制定有效合理的疏散策略，参与疏散指导能够对疏散成本的降低起到重要作用，并且能够保护被疏散者的一部分固定资产。一般情况下，在政府参与疏散引导工作时，台风灾害的风险值较高，当撤离行动所保障的生命财产安全大于在政府疏导条件下的疏散成本时，被疏散群体双方全部疏散，是系统演化的“理性状态”。

基于本文研究的结论得到如下启示：第一，在自愿撤离的条件下，系统的最优状态并非全部采取撤离策略，而是需要依据台风带来灾害的可能性不同而变化。当可能性较高时全部撤离，反之全部留下，才是系统的“理想状态”。此时，政府应该及时发布灾害相关的信息，提高风险沟通水平，帮助群众正确估计风险，采取相应行动应对台风灾害。第二，当台风来临的风险较高时，政府有必要积极参与疏散工作，采取有效的措施帮助疏导交通，帮助减少疏散成本，包括对弱势群体高疏散成本的撤离工作的支持，一方面提供疏散的交通工具，能有效缓解路网通行能力不足，帮助无车群体疏散；另一方面在避难点安置必要的应急设施和应急物资，帮助节约被疏散群体的撤离成本。第三，政府应不断提高交通仿真技术以及GIS技术的应用水平，在准确地估计台风风险的同时合理规划疏散路径，做好应急疏散预案，提高风险的应对能力，并通过制定灾后重建，巨灾保险等政策保护被疏散者的固定资产，解除被疏散群体的后顾之忧。

本文研究在一定意义上揭示了台风灾害下被疏散群体的撤离决策机制，为政府制定和完善应急疏散预案提供一定参考依据。但是本文仍存在不足：一方面，研究被疏散群体决策时，并未将其个体的人口学特征考虑在内，只将其划分成两类有差别群体，具有一定局限性；另一方面，疏散决策分析后对于交通需求的作用，在本文没有涉及。今后研究可以从以下几个方面展开：(1)将n个被疏散的个体作为博弈的主体进行分析；(2)台风灾害下疏散的交通需求预测研究等。

参考文献：

[1] 张钊.可预知灾难性事件下城市群应急交通疏散模型及分析[D].成都:西南交通大学,2013.

[2] 崔娜.台风灾害下无车群体疏散需求预测与集散设施选址研究[D].哈尔滨:哈尔滨工业大学,2012.

[3] Southworth F. Regional evacuation modeling: a state of the art reviewing[J]. Oak Ridge National Labs, 1991, 11(5): 511-521.

[4] Murray-Tuite P, Wolshon B. Evacuation transportation modeling: an overview of research, development, and practice[J]. Transportation Research Part C: Emerging Technologies, 2013, 27(2): 25- 45.

[5] Pel A J, Bliemer M C J, Hoogendoorn S P. A review on travel behaviour modeling in dynamic traffic simulation models for evacuations[J]. Transportation, 2012, 39(1): 97-123.

[6] Xie C, Lin D Y, Waller S T. A dynamic evacuation network optimization problem with lane reversal and crossing elimination strategies[J]. Transportation Research Part E: Logistics & Transportation Review, 2010, 46(3): 295-316.

[7] Kalafatas G, Peeta S. Planning for evacuation: insights from an efficient network design model[J]. Journal of Infrastructure Systems, 2009, 15(15): 21-30.

[8] Gudishala R, Wilmot C. Comparison of time-dependent sequential logit and nested logit for modeling hurricane evacuation demand[J]. Transportation Research Record Journal of the Transportation Research Board, 2012, 2312(2312): 134-140.

[9] Carnegie J, Deka D. Using hypothetical disaster scenarios to predict evacuation behavioral response[A].Transportation Research Board 89th Annual Meeting[C]. National Academy of Sciences, Washington D C, 2010.1

[10] Mei B. Development of trip generation models of hurricane evacuation[D]. Louisiana: Louisiana State University, 2002.

[11] Fu H. Sequential logit dynamic travel demand model for hurricane evacuation[J]. Transportation Research Record Journal of the Transportation Research Board, 2004, 1882(1): 19-26.

[12] Hasan S, Mesa-Arango R, Ukkusuri S. A random-parameter hazard-based model to understand household evacuation timing behavior[J]. Transportation Research Part C: Emerging Technologies, 2013, 27(2): 108-116.

[13] 马洁,徐瑞华,黄家骏.基于危险源影响的地铁车站乘客疏散仿真模型[J].系统工程理论与实践,2016,36(6):1585-1592.

[14] 张永彬,王坚,王超,等.基于SAPSO算法的人群疏散模型研究[J].管理评论,2016,28(8):152-157.

[15] 高明霞.基于双层规划的交通疏散中车辆出发与交通控制综合优化[J].中国管理科学,2014,22(12):65-71.

[16] 安实,崔建勋,王健.基于模糊逻辑与离散选择模型的混合疏散人口估计模型[J].交通运输工程学报,2009,(5):78- 82.

[17] 吴文祥,黄海军.固定需求交通网络的一般系统最优模型与性质[J].管理科学学报,2015,18(12):58- 67.

[18] 吴健宏,翁文国,倪顺江.不同路径选择策略的城市疏散仿真研究[J].系统仿真学报,2013,25(1):122-126.

[19] 陈星光,周晶,朱振涛.城市交通出行方式选择的演化博弈分析[J].管理工程学报,2009,23(2):140-142.

[20] 巩亚文.信息诱导条件下出行路径选择行为的演化博弈分析[J].公路,2015,(1):108-113.

[21] Han Q, Dellaert B, Raaij F V, et al.. Modeling impact of emerging uncertain time-dependent aggregate activity-travel patterns on individual activity participation and timing decisions[J]. Transportation Research Record Journal of the Transportation Research Board, 2004, 1894(1): 28-36.

[22] 肖海燕,王先甲.政府参与模式下出行者出行方式选择行为的演化博弈分析[J].管理工程学报,2010,24(2):115-118.

[23] 周勇,张和平,万玉田,等.人员疏散拥堵问题的博弈分析[J].中国安全科学学报,2008,18(8):131-134.

[24] Gladwin C, Gladwin H, Peacock W G. Modelling hurricane evacuation decisions with ethnographic method[J]. International Journal of Mass Emergencies & Disasters, 2001, 19(2): 117-143.