构建三角恒等式链的一种方法

刘小宁

(武汉软件工程职业学院　湖北　武汉：430205)

利用韦达定理与对称多项式知识证明三角恒等式，是初等数学研究的热点与前沿内容[1-14]，目前虽然取得一定的研究成果，但是还存在进一步丰富的空间。文中应用韦达定理，构建一元高次方程根与系数的一个关系，获得建立三角恒等式链的一种方法。

1　定理

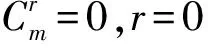
定理1：若xi(1≤i≤n)为一元n次方程

之根，记

有：f(1)=f(2)=…=f(m) =…=f(n)=1/σ0。

证明：根据韦达定理[2,3]可知

(1)

(2)

……

(3)

……

(4)

将式(1)～式(4)变形可得

由此即知定理1成立。

利用类似方法，可证明得到

定理2：若xi(1≤i≤n-1)为一元(n-1)次方程

之根，记

有：F(1)=F(2)=…=F(m) =…=F(n-1)=1/σ0。

显然，定理1与定理2构建了一元高次方程根与系数的一个新关系。

2　引理

引理1[2-8]：一元n次方程根与系数存在表1的对应关系。

表1　一元n次方程的根与系数

引理2[2-8]：一元(n-1)次方程根与系数存在表2的对应关系。

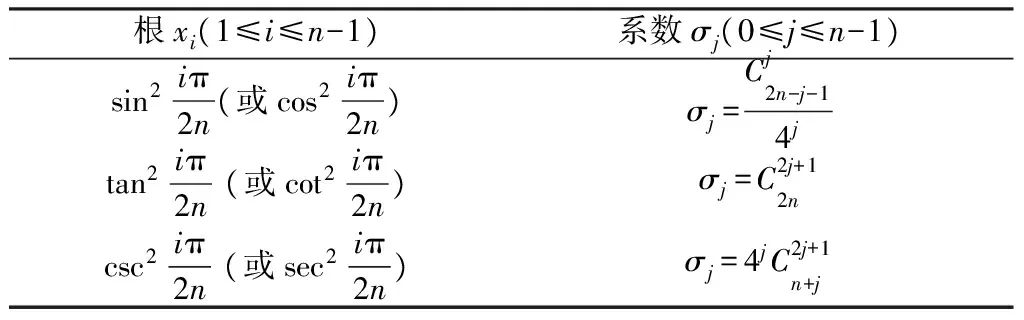
表2　一元(n-1)次方程的根与系数

3　构建三角恒等式链的方法

由定理1与引理1、定理2与引理2，可获得建立三角恒等式链的如下方法。

记

(5)

有：f1(1)=f1(2)=…=f1(m) =…=f1(n)=1。

记

(6)

有：f2(1)=f2(2)=…=f2(m) =…=f2(n)=1。

记

(7)

有：f3(1)=f3(2)=…=f3(m) =…=f3(n)=1/(2n+1)。

记

(8)

有：f4(1)=f4(2)=…=f4(m) =…=f4(n) =1/(2n+1)。

记

(9)

有：f5(1)=f5(2)=…=f5(m) =…=f5(n)=1。

记

(10)

有：f6(1)=f6(2)=…=f6(m) =…=f6(n)=1。

记

(11)

或

(12)

有：F1(1)=F1(2)=…=F1(m) =…=F1(n-1)=1。

记

(13)

或

(14)

有：F2(1)=F2(2)=…=F2(m) =…=F2(n-1)=1/(2n)。

记

(15)

或

(16)

有：F3(1)=F3(2)=…=F3(m) =…=F3(n-1)=1/n。

4　示例

根据式(5)～式(16)，可以建立形式优美的三角恒等式链与三角恒等式。

当n=3时，由式(5)～式(10)整理可得到三角恒等式链与三角恒等式的示例。

当n=4时，由式(11)～式(16)整理，可得到三角恒等式链与三角恒等式的如下示例。

显然，根据文中构建的方法，不但可得到形式优美的三角恒等式链，而且还可获得系列的三角恒等式。

[1]黄盛清.基于余弦7倍角公式求几个一元三次方程的解及其应用[J].数学通报,2017，(6):59-60.

[2]刘小宁.三角恒等式的一个来源[J].武汉工程职业技术学院学报,2013,25(2):74-76.

[3]刘小宁.获得一类三角恒等式的新方法[J].高等数学研究,2015,18(1):61-62.

[4]倪忠仁.利用韦达定理证明某些三角恒等式[J].数学通报,1982，(5):29-31.

[5]贾维玉.一类系数为组合数的高次方程[J].数学通讯,1994，(10):18-19.

[6]师五喜.也谈用韦达定理证明某些三角恒等式[J].数学通报,1996，(1):22-23.

[7]刘小宁.直接计算贝努利数的新公式[J].武汉工程职业技术学院学报,2011,23(3):79-80.

[8]陈计,叶中豪.初等数学前沿(1995)[M].南京:江苏教育出版社,1996:310-316.

[9]刘小宁.几个不常见的三角多倍角公式[J].武汉工程职业技术学院学报,2012,24(4):75-77.

[10]卢新平,王道金.构造方程证明两个三角恒等式[J].数学通报,2010,(7):50-51.

[11]刘小宁.涉及Lucas数的几个无穷级数求和[J].武汉工程职业技术学院学报,2015,27(4):82-84.

[12]刘小宁.用初等方法求一个无穷级数和[J].武汉工程职业技术学院学报,2011,23(1):79-80.

[13]刘小宁.关于Fibonacci与Lucas数的求和[J].武汉工程职业技术学院学报,2016,28(2):76.

[14]张青山.一个三角恒等式的推广的复数证明[J].数学通报,1998,(8):23.