区间变时滞不确定系统鲁棒稳定性分析
吴玉彬, 张合新, 惠俊军, 李国梁, 周 鑫, 孙大为
(1. 火箭军工程大学控制工程系, 陕西 西安710025; 2.中国人民解放军96037部队, 陕西 宝鸡 721013; 3. 火箭军士官学校基础系, 山东 青州 262500)
0 引 言
现实世界的许多动力学模型系统,例如网络控制系统、过程控制系统以及核反应堆控制系统等,在数据和物质的传输过程中,都包含非常明显的时滞。在众多的时滞类型中,区间变时滞更具代表性,它的时滞下界不一定为零,且时滞处于一个变化的区间内,常见于化学反应器、内燃机和网络控制等工程实际应用中。因而近年来,区间变时滞系统的稳定性分析[1-30]成为热门的研究领域。
对于区间时滞系统的稳定性分析,最常见的方法是采用基于时域内直接构造Lyapunov-Krasovskii泛函(Lyapunov-Krasovskii function, LKF)并结合线性矩阵不等式(linear matrix inequality, LMI)对其稳定性进行分析。在此框架下,如何降低所得结论的保守性便成为普遍关注的热点问题。就分析方法而言,有增广泛函法、自由权矩阵方法和时滞分割方法等。这些方法的共同点在于能充分利用系统的时滞信息,有效降低结论的保守性。但是随着矩阵变量的过多引入及分割数目的不断增加势必给理论分析和工程计算带来负担;于是,具有形式简单、含矩阵变量少的积分不等式界定技术作为新颖的分析方法逐渐给时滞系统的稳定性分析带来了推动作用。例如,文献[2]最早把Jensen’s不等式引入到时滞系统的稳定性分析中,随后文献[9-11]对Jensen’s不等式做了进一步推广,从而得到结论保守性更低的相关结论。
文献[13-14]通过凸组合技术,获得时滞系统稳定性分析的新颖方法。文献[13]采用交互式凸组合技术,给出LMI形式保守性更低的稳定性新判据。同样,文献[14]借助于Jensen’s不等式和交互式凸组合技术,推导出非线性时变时滞系统的稳定性判据。文献[21]采用凸组合技术估计附加时变项,获得严格约束的非线性时变系数,所得结论在稳定性方面更具优越性。
文献[22]新构造的LKF包含三重积分泛函项,优化了时滞系统的稳定性条件。文献[23-24]针对时变时滞的线性系统,通过构造包含三重积分泛函项的LKF,得到了保守性更低的稳定性判据。文献[25]构造了包含时变时滞信息的新LKF,基于新的积分不等式界定技术得到了区间时变时滞系统的时滞相关鲁棒稳定性判据。文献[29]通过构造时滞分割LKF,避开凸组合技术和自由权矩阵方法,仅仅采取更严格的界定不等式条件,给出了区间时变时滞离散系统的稳定性判据。文献[30]研究了一类不确定T-S模糊区间时变时滞系统的鲁棒稳定性,通过构造包含时滞分割特性的适当LKF,借助于更紧密界定技术的积分不等式处理交叉项,最后用数例证明了给出的稳定性条件在计算效率上具有更小的保守性。
本文针对一类区间变时滞不确定系统,提出形式简单、保守性更低的鲁棒稳定判据。该判据采用新型的时滞分割法,把时滞区间分成不均匀的两个分割区间,针对每一分割区间构造新的LKF,并采用积分不等式和交互式凸组合技术给出不包含任何多余参量的LMI形式结论。不同于以往方法,①在构造LKF时加入包含更多时滞信息的四重积分项和增广泛函项;②在处理泛函导数的交叉项时,在未忽略有用项的前提下,利用缩放程度更小的积分不等式进行界定,有利于降低结论的保守性;③采用交互式凸组合技术推导出保守性更低的稳定性判据。最后的数值仿真对比验证了本文所提判据的有效性与优越性。

1 问题描述
考虑线性区间变时滞不确定系统
(1)
式中,x(t)∈Rn为系统的状态向量;A和B为适当维数的系统矩阵;h(t)为系统状态时变时滞且满足:0≤hm≤h(t)≤hM,ΔA(t)和ΔB(t)为具有范数有界不确定性的时变结构未知矩阵且满足
(2)
式中,D、Ea和Eb为适当维数的已知矩阵;F(t)是具有可测元的不确定矩阵,且满足
F(t)TF(t)≤I,∀t.
(3)
当F(t)=0时,系统(1)变为标称系统(4)。
为证明方便,现将需用到的引理归纳如下。
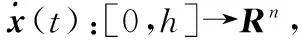
引理2[22]假定任意的矩阵M=MT>0,标量和向量函数x(t):[0,h]→Rn,则有不等式成立,即


其中
2 主要结论
本小节分两步讨论系统的稳定性,首先给出标称系统的稳定性判据,其次分析区间变时滞不确定系统的稳定性问题。
系统(1)的标称系统为
(4)
针对系统(4),通过构造包含时滞信息增广项和四重积分项的L-K新泛函,结合引理1~引理3有如下结论。
定理1对于给定标量hm、hM和λ1、λ2(λ1>λ2),且若存在正定对称矩阵Pi(i=1,2,3,4,5)、Q1、Q2、U1、U2、Xj、Rj(j=1,2,3,4),使得式(5)成立,则标称系统(4)渐近稳定。
Φ=(Φi,j)10×10<0
(5)
其中
Φ13=X2,Φ14=0,Φ15=2P2+hmR2
Φ16=(2-ε)(hM-hm)R4
Φ17=(1+ε)(hM-hm)R4
Φ23=-(α-2)X4,Φ24=(1+α)X4
Φ25=Φ26=Φ27=Φ28=Φ29=Φ210=0
Φ33=Q2-Q1-X2+(α-2)X4
Φ35=-2P2,Φ36=Φ37=2P3
Φ34=Φ38=Φ39=Φ310=0
Φ44=-Q2-(1+α)X4,Φ46=Φ47=-2P3
Φ45=Φ48=Φ49=Φ410=0,Φ55=-X1-R2
Φ56=Φ57=Φ59=Φ510=0,Φ58=-2P4
Φ66=(α-2)X3-(2-ε)R4,Φ67=Φ68=0
Φ69=Φ610=-2P5,Φ77=-(α+1)X3-(1+ε)R4
Φ78=0,Φ79=Φ710=-2P5,Φ88=-R1-U1
Φ89=Φ810=0,Φ99=-(2-ε)R3-U2
Φ910=-U2,Φ1010=(1+ε)R3-U2
证明令hΔ=γhm+(1-γ)hM, 0<γ<1,则有hm 情形1当hΔ≤h(t)≤hM时,设计LKF为 V(x(t))=V1(x(t))+V2(x(t))+ V3(x(t))+V4(x(t))+V5(x(t)) (6) 其中 计算LKFV(x(t))沿系统(4)的导数,即 (7) 其中 xT(t-hΔ)Q2x(t-hΔ)-xT(t-hM)Q2x(t-hM) 由引理1与引理2可得 (8) (9) 其中,ζ(t)同引理3中hm=hΔ时定义一致。 由引理3可得 (10) 同样可以得到 (11) (12) (13) (14) (15) (16) (17) ζT(t)[αΓ1+(1-α)Γ2+εΓ3+(1-ε)Γ4]ζ(t) (18) 其中 因为0≤α,ε≤1,根据凸组合技术,不等式(19)、不等式成立,即 α(Γ1+λ1I)+(1-α)(Γ2+λ1I)<0 (19) ε(Γ3-λ2I)+(1-ε)(Γ4-λ2I)<0 (20) 即 αΓ1+(1-α)Γ2<-λ1I (21) εΓ3+(1-ε)Γ4<λ2I (22) 由于λ1>λ2,合并式(21)、式(22),可得 αΓ1+(1-α)Γ2+εΓ3+(1-ε)Γ4<(λ2-λ1)I<0 (23) 情形2当hm≤h(t)≤hΔ时,设计LKF为 V0(x(t))=V01(x(t))+V02(x(t))+ V03(x(t))+V04(x(t))+V05(x(t)) (24) 其中 其中 Pi(i=1,2,3,4,5)、Q1、Q2、U1、U2、Xj、Rj(j=1,2,3,4) 同式(8)中所定义的矩阵。利用同样的方法,可得 εΓ03+(1-ε)Γ04]ζ0(t) (25) 其中 对式(18)或式(25)应用引理3,则其等价于式(5)。 证毕 注2在式(5)中,新的稳定性判据没有涉及冗余的自由权矩阵,只是巧妙地采用新颖的积分不等式来界定LKF导数产生的交叉项,并利用极少数自由矩阵表示相关项之间的关系,因此大大减少了理论推导和计算上的复杂性,从而降低了结论的保守性。 注3在式(10)、式(11)和式(14)中,交互式凸组合处理技术[13,27]作为非传统方法用来更有效地界定LKF导数产生的交叉项,可以得到保守性更低的稳定性结论。 定理2对于给定标量hm、hM和λ1、λ2(λ1>λ2)、μ,且若存在正定对称矩阵Pi(i=1,2,3,4,5)、Q1、Q2、Q3、U1、U2、Xj、Rj(j=1,2,3,4),使得LMIs成立,即 (26) 下面针对区间变时滞不确定系统(1)的鲁棒稳定性问题进行研究。 定理3对于给定标量0 (27) 则不确定系统(1)渐近稳定。其中 证明对于不确系统(1),分别以A+ΔA(t),B+ΔB(t)代替式(4)中的A和B,仿照定理1的证明,可得到系统(1)渐近稳定。 证毕 通过3个具有代表性的数值例子来比较说明本文方法的优越性。利用Matlab的LMI工具箱很容易求得所需要的可行性解。最大允许时延(maximum allowable delay bound, MADB)定义为保证系统稳定的最大允许时滞上界值,是比较时滞系统稳定性结论保守性最普遍的衡量标准。 例1首先考虑区间变时滞闭环控制系统为 针对不同的时滞下界hm,根据式(26)和式(5),分别从时滞变化率μ=0.3和时滞变化率μ取任意值两个角度,仿真给出相应的MADB值即hM如表1和表2所示。 表1 例1中针对不同的时滞下界,不同方法仿真给出的MADB值 表2 例1中当时滞变化率未知时,不同方法仿真给出的MADB值 由表1和表2可知,本文提出的方法明显优于已有文献的结论。 例2考虑区间变时滞不确定系统,即 式中,δ1,δ2,δ3和δ4为未知参数,满足:|δ1|≤1.6,|δ2|≤0.05,|δ3|≤0.1,|δ4|≤0.3。 针对不同的时滞下界hm,根据式(26),仿真给出相应的MADB值即hM如表3所示。 表3 例2中针对不同的时滞下界,不同方法仿真给出的MADB值 由表3的比较结果可知,对于本例而言,本文方法改善了现有文献[5,9,16,25]的结论。 例3考虑另一区间变时滞不确定系统,其系统参数为 根据式(27),针对不同的时滞下界hm,当时滞变化率未知时,仿真给出相应的MADB值即hM如表4所示。 表4 例3中针对不同的时滞下界,不同方法仿真给出的MADB值 由表4可知,本文所提出的稳定性判据扩大了保证系统稳定的最大允许时滞上界范围,具有更低的保守性。 针对一类区间变时滞不确定系统的鲁棒稳定性问题进行了分析研究。基于新型的非均匀时滞分割法,通过构造包含四重积分增广泛函项的新LKF,提出了基于LMI的稳定性新判据。为了提高计算效率并简化结论,该判据避免使用模型变换与自由权矩阵界定技术,取而代之的是采用具有更紧密界定技术的积分不等式和交互式凸组合技术,从而充分利用了时滞下界信息,获得了保守性更低的结论。最后,数值仿真证明了所得判据相比较已有文献中的方法,扩大了系统稳定所允许的最大时滞上界范围,更具优越性与竞争性。 参考文献: [1] GAHINET P, NEMIROVSKI A, LAUB A J, et al. LMI control toolbox user’s guide[J].1995. [2] GU K, KHARITONOV V L, CHEN J. Stability of time-delay systems[M]. Boston: Birkhäuser, 2003. [3] HE Y, WANG Q G, LIN C, et al. Delay-range-dependent stability for systems with time-varying delay[J].Automatica,2007,43(2): 371-376. [4] HE Y, WANG Q C, XIE L, et al. Further improvement of free weighting matrices technique for systems with time-varying delay[J]. IEEE Trans.on Automatica Control, 2007, 52(2): 293-299. [5] JIANG X F, HAN Q L. New stability criteria for linear systems with interval time varying delay[J]. Automatica, 2008, 44(10): 2680-2685. [6] PENG C, TIAN Y. Delay-dependent robust stability criteria for uncertain systems with interval time-varying delay[J]. Journal of Computational and Applied Mathematics, 2008, 214(2): 480-494. [7] SHAO H. Improved delay-dependent stability criteria for systems with a delay varying in a range[J]. Automatica,2008,44(12): 3215-3218. [8] SHAO H Y. New delay-dependent stability criteria for systems with interval delay[J]. Automatica, 2009, 45(3): 744-749. [9] RAMAKRISHNAN K, RAY G. Delay-dependent robust stability criteria for linear uncertain systems with interval time varying delay[C]∥Proc.of the TENCON 2009-2009 IEEE Region 10 Conference, 2009: 539-543. [10] RAMAKRISHNAN K, RAY G. Robust stability criteria for uncertain linear systems with interval time-varying delay[J]. Journal of Control Theory and Applications, 2011, 9(4): 559-566. [11] 张合新,惠俊军,周鑫,等.基于时滞分割法的区间变时滞不确定系统鲁棒稳定新判据[J].控制与决策,2014,29(5):907-912. ZHANG H X, HUI J J, ZHOU X, et al. New robust stability criteria for uncertain systems with interval time-varying delay based on delay-partitioning approach[J]. Control and Decision, 2014, 29(5): 907-912. [12] YUE D, TIAN E, WANG Z, et al. Stabilization of systems with probabilistic interval input delays and its applications to networked control systems[J]. IEEE Trans.on Systems, Man and Cybernetics, 2009, 39(4): 939-945. [13] ZHU X L, WANG X Y, YANG G H. New stability criteria for continuous-time systems with interval time-varying delay[J]. IET Control Theory Applications, 2010, 4(6): 1101-1107. [14] AN J Y, LI Z Y, WANG X M. A novel approach to delay-fractional dependent stability criterion for linear systems with interval delay[J]. ISA Trans., 2014, 53(2): 210-219. [15] ZHANG W, CAI X S, HAN Z Z. Robust stability criteria for systems with interval time-varying delay and nonlinear perturbations[J]. Journal of Computational and Applied Mathematics, 2010, 234(1): 174-180. [16] PARK P, KO J W, JEONG C. Reciprocally convex approach to stability of systems with time-varying delays[J]. Automatica, 2011, 47(1): 235-238. [17] KWON O M, LEE S M, PARK J H. Linear matrix inequality approach to new delay-dependent stability criteria for uncertain dynamic systems with time-varying delays[J]. Journal of Optimization Theory Applications, 2011, 149(3): 630-646. [18] LI T, SONG A, XUE M, et al. Stability analysis on delayed neural networks based on an improved delay-partitioning approach[J]. Journal of Computational and Applied Mathematics, 2011, 235(9): 3086-3095. [19] WANG C, SHEN Y. Delay partitioning approach to robust stability analysis for uncertain stochastic systems with interval time-varying delay[J]. IET Control Theory and Applications, 2012, 6(7): 875-883. [20] TANG M, WANG Y W, WEN C. Improved delay-range-dependent stability criteria for linear systems with interval time-varying delays[J]. IET Control Theory and Applications, 2012, 6(6): 868-873. [21] PHAT V N, KHONGTHAM Y, RATCHAGIT K. LMI approach to exponential stability of linear systems with interval time-varying delays[J]. Linear Algebra and Its Applications, 2012, 436(1): 243-251. [22] SUN J, LIU G P, CHEN J. Delay-dependent stability and stabilization of neutral time-delay systems[J]. International Journal of Robust Nonlinear Control, 2009, 19(12): 1364-1375. [23] SUN J, LIU G P, CHEN J, et al. Improved stability criteria for linear systems with time-varying delay[J]. IET Control Theory Applications, 2010, 4(4): 683-689. [24] SUN J, LIU G P, CHEN J, et al. Improved delay-range-dependent stability criteria for linear systems with time-varying delays[J]. Automatica, 2010, 46(2): 466-470. [25] LIU P L. Further improvement on delay-range-dependent stability results for linear systems with interval time-varying delays[J]. ISA Transaction, 2013, 52(6): 725-729. [26] LEE W, PARK P. Second-order reciprocally convex approach to stability of systems with interval time-varying delays[J]. Applied Mathematics and Computation, 2014, 229(10): 245-253. [27] FARNAM A, ESFANJANI R M. Improved linear matrix inequality approach to stability analysis of linear systems with interval time-varying delays[J]. Journal of Computational and Applied Mathematics, 2016, 294(C): 49-56. [28] FARNAM A, MAHBOOBI ESFANJANI R. Improved stabilization method for networked control systems with variable transmission delays and packet dropout[J]. ISA Transaction, 2014, 53 (6): 1746-1753. [29] ZHANG J, PENG C, ZHENG M. Improved results for linear discrete-time systems with an interval time-varying input delay[J]. International Journal of Systems Science, 2015, 47(2): 492-499. [30] PENG C, FEI M R. An improved result on the stability of uncertain T-S fuzzy systems with interval time varying delay[J]. Fuzzy Sets and Systems, 2013, 212(1): 97-109.
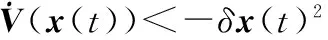



3 数值仿真与比较
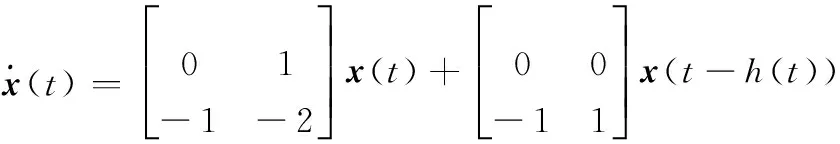




4 结 论

