退化相关多部件系统预防性维修决策模型

杨志远, 赵建民, 程中华

(陆军工程大学石家庄校区装备指挥与管理系, 河北 石家庄 050003)

0　引　言

随着技术的发展,现代工业设备结构越来越复杂,相应的价值和停机造成的损失也越来越高,维修对于降低系统故障率和减少使用成本具有重要的意义。在复杂系统中,各部件间的退化失效往往具有相互影响,这就使得这类系统的维修决策变得更为复杂,如果将此类系统的维修决策问题按照独立退化过程来处理,将会影响维修决策的科学性乃至正确性。

部件间的相关关系可划分为经济相关、结构相关和故障相关,近年来,在复杂系统维修决策研究中,最受关注的是对故障相关性的研究。故障相关也称随机相关,是指一个部件的状态会影响其他部件的状态。这里的“状态”包括寿命、故障率、故障状态等各种状态度量标准。目前,在故障相关研究中最常见的是考虑故障率之间的相关关系,这种方法是建立在多部件系统故障失效随机数据基础上的。在关于故障相关的早期研究中,文献[1-2]提出了多部件系统中存在的3种类型的故障相关;文献[3]考虑两部件并联系统在交叉检测下的可靠度问题,其中一个部件故障后将以概率p影响另一个部件的故障概率。文献[4]建立了一个解析模型用于定量分析部件间的相关故障率。文献[5]假设两部件可修复系统中故障相关是单向的,在此基础上,建立了周期性检测优化模型。另外共因失效也是一种特殊的故障相关表现,目前关于共因失效的研究也可以认为是基于故障率相关的,共因失效增大了系统各失效模式间的联合失效概率[6],关于其研究可参考文献[7-8]。故障率交互的方法是基于故障失效数据的,在实际中,有些设备的可靠度较高因而能获得的故障数据较少[9],会限制该方法的应用,而且由于复杂系统各个部件的独立故障率难以通过失效数据统计得到,因此也很难推导故障率之间的相互影响关系。

故障相关性另一种研究方法是基于退化过程相关开展的,通过各部件退化过程间的相互影响来对部件间的相关性进行分析研究。目前关于退化过程相关的研究文献还较少,比较常用的是用两变量退化分布模型[10-12]和Copula函数[13-14]来表现复杂系统不同部件退化量间的相关关系。使用两变量退化分布模型和Copula函数难点在于确定相关函数的形式,就Copula法来说,常见的Copula函数有Gumbel Copula、Clayton Copula、Frank Copula、Gaussian Copula、t-Copula等[15],确定系统适合的Copula函数及相关参数比较困难。退化过程相关也可用部件退化速率之间的关系表示,目前采用此种方法的研究还较少且相关维修策略较为单一,在维修决策模型中也通常只考虑两部件相关,文献[16]运用退化速率相关的方法研究了多部件系统部件退化间的相关关系模型并提出了相应的基于状态维修策略,但模型采用数据驱动的方法,没有建立关于部件退化过程相互影响的解析模型,也未得到相应的退化过程显式模型,这限制了对该方法的深入研究和使用。

基于此,本文在非线性Wiener退化过程模型基础上,考虑退化速率影响建立了退化相关多部件系统退化过程解析模型和可靠度模型,并提出了相应的预防性维修策略,以单位时间维修费用最小为目标建立了预防性维修决策优化模型,进而得到了系统最优预防性维修策略,以提高这类系统维修活动的经济效益。

1　退化过程模型

在现有退化过程模型中,常用的包括退化轨迹模型、退化量分布模型、累积损伤模型、Gamma过程模型以及Wiener过程模型,其中Gamma过程模型与Wiener过程模型是常用的随机过程模型。由于Wiener过程模型能够描述多种典型产品的性能退化过程,并且具有良好的计算性质,因而是目前性能可靠性建模领域较常用的退化模型之一。本文中采用非线性Wiener过程模型来建立部件退化模型,令X(t)表示部件在时刻t的退化量,那么X(t)可表示为

(1)

式中,λ(t;ϖ)是关于时间t的连续非减函数,表示退化过程的平均趋势,ϖ为影响退化过程的相关参数;B(t)为标准布朗运动,表示退化过程中的随机性。可以看出,如果令λ(t;ϖ)=λ,那么模型就变为了线性Wiener过程模型;如果令σB=0,那么模型将退化为真实退化路径模型。为便于分析,令X(0)=0,即在开始时刻0部件的退化量为0,用X(t)表示部件的累计退化量,则有

(2)

在此基础上,进一步设定

(3)

式中,μ(t;ϖ)表示的是期望退化量随时间的变化情况。由此,部件退化非线性Wiener过程模型可表示为

X(t)=μ(t;ϖ)+σBB(t)

(4)

假设系统由n个部件组成,部件退化过程中存在相关关系。根据建立的退化模型,n个部件退化过程模型可表示为

X(t)=μ(t;ϖ)+σBB(t)

(5)

式中,X(t),μ(t;ϖ)和σB均为n维列向量,表示不同部件的退化模型。可以看出,退化量X(t)由两部分组成,第二部分表示的是部件在退化过程中的随机性因素,假设对于不同的部件随机性因素是相互独立的,所以在本文中采用μ(t;ϖ)描述不同部件退化过程间的相互关系。

在系统运行过程中,部件的退化会对与其具有相关关系部件的退化速率产生影响,这是由于某些部件的退化造成了整个系统在非正常状况下运行,这会影响相关部件的退化速率。以齿轮箱为例,轴承的磨损将会造成过量的振动,因此相关的齿轮退化速度也会加快,反之,齿轮的磨损也会导致轴承的加速退化。为方便实际应用,本文中采用退化量期望值的变化定义部件在t时刻的退化速率,表示为

(6)

基于此,借鉴文献[16]中的退化率相关法和文献[18]中相关故障率的概念,建立部件退化相关解析模型为

ϖ)=Θn×nμ(t;ϖ)+Q(t)

(7)

式中,Θn×n是部件间的相关系数矩阵,表示部件退化间相关关系的强弱;Q(t)表示部件的固有退化率。以上参数可由系统或类似系统历史退化数据或实验数据估计得到,以较小时间间隔Δt对各部件的退化状态进行取样,令ΔXt=Xt+Δt-Xt,根据式(5),可得到ΔXt=μ(t+Δt;ϖ)-μ(t;ϖ)+σBB(t+Δt)-σBB(t),由Wiener过程可得

(8)

基于此,可采用最大似然估计法对Θn×n和Σ的值进行估计;对于Q(t)可参照文献[16]中所采用的回归方法得到,这里不再赘述。

式(7)表示部件退化速率受到其自身和具有相关关系部件退化量的影响。为便于理解,将式(7)展开为

(9)

式中,θij为部件j累积退化量对部件i退化速率的影响,θij=0表示部件j对部件i无影响。如果θij为常数,式(7)可以看作一个常系数线性非齐次微分方程组,根据线性非齐次微分方程组解的存在与唯一定理,给定相应的初始条件,那么式(7)存在唯一解。通过求解式(7),就可以求得相应的μ(t;ϖ),进而得到各部件退化过程模型X(t)。为求解式(7),引入线性微分算子L,L表示为

(10)

引入线性微分算子L后,式(7)可简化表示为

L[μ(t;ϖ)]=Q(t)

(11)

其对应的齐次常微分方程组形式为

L[μ(t;ϖ)]=0

(12)

根据微分方程组解得结构性质,式(11)的解可表示为

(13)

根据Cayley-Hamilton定理[19]可以得到φ(t)的表达式为

(14)

式中,P0=E;Pj=(Θ-λjE)(Θ-λj-1E)…(Θ-λ1E);j=1,2,…,n。其中,λ1,λ2,…,λn是矩阵Θ的特征根(不一定相异),而函数γj(t)(j=1,2,…,n)是微分方程组式(15)初值问题的解。

(15)

(16)

由此可得部件退化相关模型式(7)的通解为

(17)

给定系统各部件的初始退化量μ(t0;ϖ)=μ0,即可得到具有退化相关关系各部件的期望退化量函数为

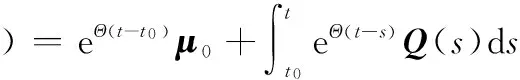
(18)

在此基础上,将式(18)代入式(5)中,可得部件退化过程模型为

(19)

2　可靠度模型

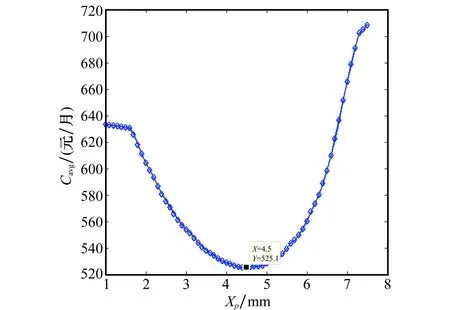
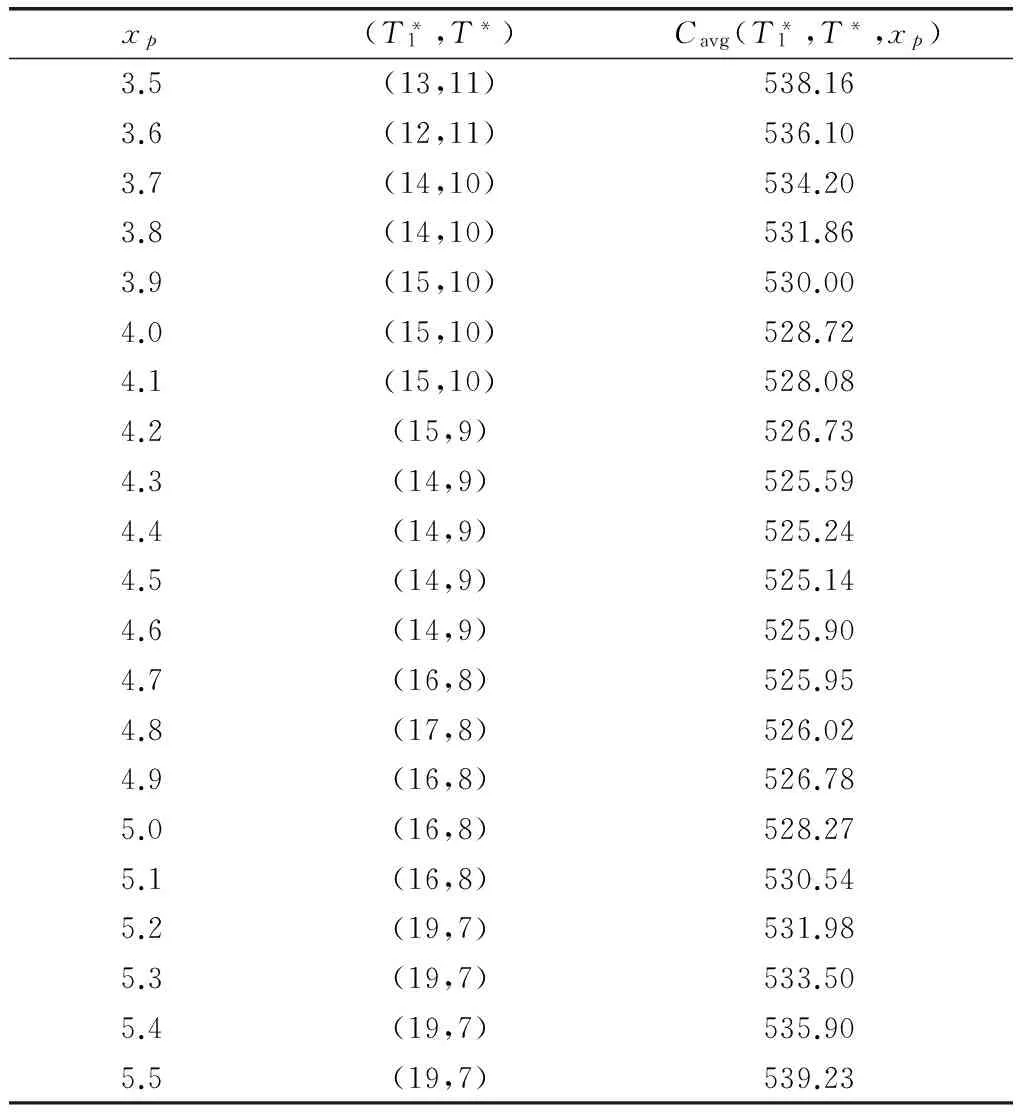
由于本文在退化建模中采用的是非线性Wiener过程模型,然而由于退化模型的复杂性,难以得到部件精确的故障分布函数。为此,考虑到在实际中部件退化过程一般是非减的,做出假设:对于任意t>s≥0,部件退化量X(t)

2.1　部件可靠度

根据式(19)可得到退化量在t时刻的分布Gt(x),定义

Gt(x)=Pr{X(t)≤x}

(20)

用T(x)表示退化量达到一定水平x时的随机时间,定义

Fx(t)=Pr{T(x)≤t}

(21)

基于以上假设,容易得到当且仅当T(x)>t时,X(t)≤x,因此Gt(x)和Fx(t)之间存在关系为

Gt(x)=1-Fx(t)

(22)

假设退化过程的故障阈值为D,在本文中,部件故障仅由退化引起,不考虑偶然故障影响,也就是说,当退化水平X(t)超过阈值D时，部件出现故障。那么根据假设和可靠度的定义,部件的可靠度函数可表示为

RD(t)=Gt(D)=1-FD(t)

(23)

(24)

式中,Φ(·)表示标准正态分布。

Ψt(x;u)=Pr{ΔXt(u)≤x}=

(25)

2.2　系统可靠度

根据部件退化相关模型可以看出,部件退化间的相互关系是通过μ(t;ϖ)来表示的。而退化模型中σBB(t)只与时间相关,不同部件之间σBB(t)是相互独立的,当时间一定时,μ(t;ϖ)是固定值,所以不同部件间是否发生故障(退化量是否超过故障阈值)可认为相互独立。因此,系统可靠度函数可表示为

(26)

3　系统预防性维修模型

3.1　基本假设与预防性维修策略

在建立预防性维修模型之前,做出以下基本假设:

假设1任意部件故障都会造成系统故障,系统故障是由不同部件故障引起的竞争失效过程,系统一旦发生故障则会立即停止运行并被发现。

假设2部件的退化状态只能通过检测得到,且检测是完善的,即通过检测能够精确地得到部件退化状态。

假设3系统由1个核心部件和n-1个辅助部件组成,任何一个部件的故障都将导致系统出现功能故障,核心部件是指价值较高、功能重要且发生故障造成损失较大的部件。需要注意，本文中的“部件”既可以是单个部件,也可以指一个子系统,本文中所指的核心部件是符合上述特点,有必要进行定期检测的部件组成的子系统。

图1　系统预防性维修策略

在以上预防性维修策略下,由于部件退化间的相互关系,部件在每个间隔期内的退化过程有所差异。假设部件在第i个预防性维修间隔内t时刻期望退化量记为μi(t;ϖ),为了便于以下模型推导,令每个预防性维修间隔期均从0时刻开始,即0≤t≤Ti。在任意间隔期内,部件退化间的相互关系模型是相同的,均由式(7)给出,所以式(16)给出的通解在每个预防性维修间隔期内均适用,只需改变相应的初始条件即可。对部件进行更换使得部件修复如新,即退化量变为0,因此,在第i个预防性维修间隔期内模型初始条件可表示为

向量中第一项是对于核心部件来说的,由于对其进行检测不影响退化量,在第i个间隔期初始退化量等于第i-1个间隔期结束时的退化量,其中对核心部件退化模型存在μ1(0;ϖ)=μ0(T0;ϖ)=0。由此,可得到在第i个预防性维修间隔期内部件的退化过程模型为

(27)

在式(27)基础上,根据式(23)可得到各部件在各预防性维修间隔期内的可靠度和故障分布函数。

已经给出了部件可靠度和故障分布函数,但对于核心部件而言,由于其采用功能检测策略,所以其发生故障更新或预防性更换的概率不能由可靠度函数简单得到,需要分情况进行讨论。

当i=1时,即在第一个预防性维修间隔期内,发生故障更新或预防性更换的概率较为简单,根据部件可靠度函数及功能检测策略,其分别为FD,1(T1)和GT1,1(D)-GT1,1(xp)。符号Gt,i(x)=Pr{Xi(t)≤x},表示在第i个预防性维修间隔期内的Gt(x)函数,其他相关符号表示相同,下面不再赘述。

当i≥2时,核心部件首次更新发生在第i个预防性维修间隔期内t时刻前故障更新的概率为

HD,i(t)=Pr{Xi(0)

Pr{Xi(0)

(28)

式中,g0,i(x)=dG0,i(x)/dx。

核心部件在第i个预防性维修间隔期内t时刻前未出现部件更新的概率为

Pr{Xi(0)

Pr{Xi(0)

(29)

核心部件在第i次检测时出现预防性更换更新的概率为

Pr{Xi(0)

Pr{Xi(0)

(30)

(31)

式中,EC表示每个更新周期内系统维修费用期望值；EL表示系统期望更新周期长度。

在预防性维修策略中,系统有两种可能的更新方式,一种是由于任意部件故障引起的系统故障更换,称为故障更新;另一种是由于核心部件在检测时，退化量在预防性更换阈值xp和故障阈值D之间引起的系统预防性更换,称为检测更新。

3.2　系统维修总费用

(32)

当i≥2时,根据系统故障更新是否由核心部件(假设核心部件编号为1)发生故障引起,考虑两种情况,和首次预防性维修间隔期内故障更新概率计算原理类似,可得在第i个预防性维修间隔期内,系统故障更新概率为

(33)

(34)

基于此,可得到系统更新周期内故障更新期望费用为

(35)

系统检测更新是由核心部件预防性更换引起的,而核心部件第i次检测时发生预防性更换的概率已在之前推导给出,如式(29)所示,综合所有可能的检测点(i=1,2,…)即可得到系统检测更新发生的概率,在此基础上,可得到系统更新周期内检测更新期望费用为

(36)

综合系统更新周期内故障更新和检测更新期望费用,可得到每个更新周期内系统维修费用期望值

EC=ECfs+ECps

(37)

3.3　系统更新周期长度

在计算期望更新周期长度时,和维修费用模型类似,也可划分为故障更新和检测更新,更新概率在维修模型中已得到。在此基础上,可得到故障更新期望周期长度为

(38)

检测更新期望周期长度为

(39)

综合系统更新周期内故障更新和检测更新期望周期长度,可得到系统期望更新周期长度为

EL=ELfs+ELps

(40)

将式(37)和式(40)代入式(31)中即可得到系统单位时间维修费用Cavg(T1,T,xp)的表达式。

(41)

4　算例分析

假设系统由两个部件(子系统)组成,不失一般性,令部件1为核心部件,部件2为辅助部件,两部件退化间存在相关关系,任意部件故障都会引起系统失效,系统故障是竞争失效过程。为减少系统维修费用,采用所提预防性维修策略对系统进行维修,退化和维修模型相关参数设定如表1所示,为方便分析,费用单位统一设置为元,部件退化量单位为毫米(mm),时间单位为月,在以下叙述中不再重复标明。

基于退化过程相关模型和预防性维修策略,可利用非线性Wiener过程的独立增量特性生成部件退化过程的仿真轨迹。当T1=25,T=10时,对两部件的退化过程独立仿真5次,得到的仿真轨迹如图2所示。

表1　模型参数设置

图2　预防性维修策略下部件仿真退化轨迹

可以看出,两个部件的退化过程均呈现明显的递增趋势,且两部件退化间有明显的相关关系,如随着部件1的退化量增加,部件2的退化速率也明显加快,在相同时间内的退化量增加;对部件2进行预防性更换时,部件1的退化速率也会相应变慢,退化仿真轨迹出现转折。如果不考虑部件间退化的相互影响,即任意部件维修活动不会影响其他部件的退化过程,将会对维修决策优化结果产生影响,在下面的维修费用分析中将详细说明。

在得到退化过程模型基础上,为得到部件可靠度函数,将部件退化近似做非减退化过程处理,为验证该方法的合理性和精确性,在以上参数设置下对部件1和部件2首次到达故障阈值时间进行仿真,分别取样5 000次,做出首次故障时间的直方图,得到其近似分布,与解析故障密度函数进行对比,如图3所示。

图3　首次故障时间仿真数据和解析分布对比

由结果图仿真数据和解析分布对比可以看出,所提方法可较为精确地得到部件的故障分布函数,也验证了当σB较小时,部件非减退化过程假设的合理性。在此基础上,对系统首次故障时间进行仿真,同样取样5 000次,得到系统故障时间分布仿真数据与解析分布对比图,结果显示系统可靠度函数式(25)可较为精确地描述系统真实故障分布情况。在用迭代法搜寻模型最优值的过程中,为方便预防性维修策略的实施,预防性维修间隔期的搜索步长取1,即只在整数范围内求预防性维修间隔期的最优值。当预防性维修间隔期(T1,T)确定时,根据优化模型可得到系统单位时间维修费用Cavg(T1,T,xp)随预防性更换阈值xp的变化情况,如图4所示。

图4　xp与Cavg(T1,T,xp)的关系

图4中列举了4种不同预防性维修间隔期下单位时间维修费用随xp的变化情况,显示了对于固定的(T1,T),存在最优的预防性维修阈值xp使得单位时间维修费用最小。从整体上看,随着预防性维修间隔期的减小,xp的最优值是逐渐增大的,这是由于较小的预防性维修间隔期可以更为及时地检测系统退化量,从而可以在部件达到故障阈值前设置更大的预防性维修阈值以充分利用部件使用寿命。较小的xp值会引起系统过早更换,而较大的xp值则可相对减少过早更换，但同时会增加系统故障风险,这都会导致维修费用增加。同时通过曲线的对比可以说明区分首次预防性维修间隔期与重复预防性维修间隔期的必要性。

当预防性更换阈值xp固定时,系统单位时间维修费用Cavg(T1,T,xp)与预防性维修间隔期(T1,T)的关系如图5所示(以xp=5为例)。由系统维修费用率变化三维图和等高线图可以看出,对于固定的xp,从整体上看,无论是随着T1或T的增大,Cavg(T1,T,xp)呈现先降低后升高的趋势,这是预防性维修费用减少和故障更换费用增加共同作用结果。存在最优的(T1,T)使得系统单位时间维修费用最小,例如当xp=5时,最优预防性维修间隔期为T1=16,T=8,此时系统单位时间维修费用为528.27元。

在不考虑部件间相互影响的条件下,两部件的退化过程不会随着另一个部件的维修发生变化,所以此时两部件退化过程可由第一次预防性维修间隔期内的退化模型表示,图5(b)中的T1=25,T=4点表示在这种情况下对应的优化结果,可以看出如果部件间相互影响,所得到的实际费用和预防性维修间隔期并不是最优值。

图5　(T1,T)与Cavg(T1,T,xp)的关系(xp=5)

在以上分析基础上,对不同xp取值下的模型进行优化,得到相应的最优预防性维修间隔期和系统单位时间维修费用值,如图6所示。

图6　不同xp下系统最小单位时间维修费用

表2　不同xp对应优化结果

在预防性维修策略实施过程中,由于工作任务或者其他一些因素影响,可能不能严格按照最优预防性维修间隔期对部件实施检测和预防性更换工作,这时就需要分析预防性维修间隔期变化对系统单位时间维修费用产生的影响。

表3　不同(T1,T)下系统单位时间维修费用

5　结　论

本文在非线性Wiener退化过程模型基础上提出了基于退化速率的退化相关多部件系统退化过程模型和可靠度模型,在此基础上,建立了系统预防性维修决策优化模型。在模型算例分析部分,通过对不同部件的退化过程仿真说明了部件间的相关关系;通过仿真数据和解析分布的对比,验证了可靠度模型的精确性;通过优化得到了系统最优预防性维修策略,对比说明了最优预防性维修策略的经济效益。最后分析了决策变量变化对维修费用的影响,为预防性维修策略的实施提供参考。

参考文献：

[1] MURTHY D, NGUYEN D. Study of two-component system with failure interaction[J].Naval Research Logistics,1985,32(2): 239-247.

[2] MURTHY D, NGUYEN D. Study of a multi-component system with failure interaction[J]. European Journal of Operational Research, 1985, 21(3): 330-338.

[3] ZEQUEIRA R I, BERENGUER C. On the inspection policy of a two-component parallel system with failure interaction[J]. Reliability Engineering and System Safety, 2005, 88(1): 99-107.

[4] SUN Y, MA L, MATHEW J. An analytical model for interactive failures[J]. Reliability Engineering and System Safety, 2006, 91(5): 495-504.

[5] GOLMAKANI H R, MOAKEDI H. Periodic inspection optimization model for a two-component repairable system with failure interaction[J].Computers and Industrial Engineering,2012,63(3): 540-545.

[6] 周金宇, 谢里阳, 王学敏. 多状态系统共因失效分析及可靠性模型[J]. 机械工程学报, 2005, 41(6): 66-70.

ZHOU J Y, XIE L Y, WANG X M. Analysis for common cause failure and reliability model in multi-state systems[J]. Journal of Mechanical Engineering, 2005, 41(6): 66-70.

[7] LEVITIN G. Incorporating common-cause failures into non-repairable multistate series-parallel system analysis[J]. IEEE Trans.on Reliability, 2001, 50(4): 380-388.

[8] 李春洋,陈循,易晓山,等.基于马尔可夫过程的k/n(G)系统共因失效分析[J].系统工程与电子技术,2009,31(11):2793-2796.

LI C Y, CHEN X, YI X S, et al. Analysis of k-out-of-n: G systems subject to common cause failures based on Markov process[J]. Systems Engineering and Electronics, 2009, 31(11): 2793-2796.

[9] HSIEH M H, JENG S L, SHEN P S. Assessing device reliability based on scheduled discrete degradation measurements[J]. Probabilistic Engineering Mechanics, 2009, 24(2): 151-158.

[10] SARI J K, NEWBY M J, BROMBACHER A C. Bivariate constant stress degradation model: LED lighting system reliability estimation with two-stage modeling[J]. Quality and Reliability Engineering International, 2009, 25(8): 1067-1084.

[11] PAN Z, BALAKRISHNAN N. Reliability modeling of degradation of products with multiple performance characteristics based on gamma processes[J]. Reliability Engineering and System Safety, 2011, 96(8): 949-957.

[12] PAN Z, BALAKRISHNAN N, SUN Q, et al. Bivariate degradation analysis of products based on wiener processes and copulas[J]. Journal of Statistical Computation and Simulation,2013,83(7): 1316-1329.

[13] KAISHEV V K, DIMITROVA D S, HAVERMAN S. Modeling the joint distribution of competing risks survival times using copula functions[J]. Insurance, Mathematics and Economics, 2007, 41(3): 339-361.

[14] WANG Y P, PHAM H. Modeling the dependent competing risks with multiple degradation processes and random shock using time-varying copulas[J]. IEEE Trans.on Reliability, 2012, 61(1): 13-22.

[15] 郭驰明.基于独立增量过程的视情维修优化方法研究[D].长沙: 国防科技大学, 2013.

GUO C M. Condition-based maintenance optimization with independent increments processes[D]. Changsha: National University of Defense Technology, 2013.

[16] RASMEKOMEN N, PARLIKAD A K. Condition based maintenance of multi-component systems with degradation state-rate interactions[J]. Reliability Engineering and System Safety, 2016, 148(1): 1-10.

[17] 刘次华.随机过程[M].5版.武汉:华中科技大学出版社,2014: 21-22.

LIU C H. Stochastic process[M]. 5th ed. Wuhan: Huazhong University of Science and Technology Press, 2014: 21-22.

[18] SUN Y, MA L, MATHEW J. Failure analysis of engineering systems with preventive maintenance and failure interactions[J]. Computer and Industrial Engineering, 2009, 57(1): 539-549.

[19] 焦宝聪.常微分方程[M].北京:清华大学出版社,2008:177-178.

JIAO B C. Ordinary differential equations[M]. Beijing: Tsinghua University Press, 2008: 177-178.

[20] BAE S J, KUO W, KVAM P H. Degradation models and implied lifetime distributions[J]. Reliability Engineering and System Safety, 2007, 92(5): 601-608.

[21] LIU B, XU Z G, XIE M, et al. A value-based preventive maintenance policy for multi-component system with continuously degrading components[J]. Reliability Engineering and System Safety, 2014, 132(132): 83-89.

[22] WANG X L, BALAKRISHNAN N, GUO B. Residual life estimation based on a generalized wiener degradation process[J].Reliability Engineering and System Safety,2013,124(4):13-23.