一个包含两个数论函数方程的解

张四保，官春梅

(喀什大学数学与统计学院，新疆 喀什 844008)

0　引言

对任意正整数n，φ(n)为Euler函数，其取值为序列0，1，2，…，n-1中与n互素的数的个数.[1]Euler函数φ(n)是数论中的一类重要函数，对它的研究可谓丰富多彩.

对于方程φ(x)=n的解以及解的个数问题，许多学者进行过研究.[2-5]对于方程kφ(n)=n-1解的问题，Lehmer[6]证明了：当k=2时，该方程的解至少是7个互异奇素数的乘积；当k=3时，该方程的解至少是33个互异奇素数的乘积.1963年，柯召与孙琦[7]将这一结论进行了改进，证明了：当k=2时，方程kφ(n)=n-1的解至少是12个互异奇素数的乘积；当k=3时，方程kφ(n)=n-1的解至少是97个互异奇素数的乘积.

对于方程φ(xy)=k(φ(x)+φ(y))解的研究也有很多.文献[8-9]研究了k=3时的情况；文献[10]研究了k=7时的情况.对于方程φ(xyz)=k(φ(x)+φ(y)+φ(z))的解也有所研究.[11-12]

定义ω(n)为正整数n相异素因数的个数.对于包含φ(n)与ω(n)两个数论函数的方程的解的讨论也引起了众多学者的兴趣.文献[13]讨论了方程φ(n)=2ω(n)的解，给出了其全部的6个解；文献[14]讨论了方程φ(φ(n))=2ω(n)的解，给出了其全部的20个解；文献[15]讨论了方程φ(φ(φ(n)))=2ω(n)的解，给出了其全部的59个解；文献[16]讨论了方程φ(n)=2tω(n)的解，给出了t≤230的所有解以及t>230时的33个具体解.

本文将探讨方程φ(n)=2ω(n)3ω(n)的解，利用初等方法并结合Euler函数φ(n)的有关性质，给出了该方程的全部解，确定了该方程共有30个解.

1　主要结论

定理1方程

φ(n)=2ω(n)3ω(n)

(1)

有解n=1，7，9，57，63，74，76，399，494，518，532，654，666，684，702，756，810，3 458，4 218，4 446，4 578，4 662，4 788，4 890，4 914，5 130，31 122，34 230，35 910，49 210.

证明当n=1时，φ(1)=1，2ω(n)3ω(n)=2ω(1)3ω(1)=2030=1，因而n=1是方程(1)的解.

(2)

(3)

(4)

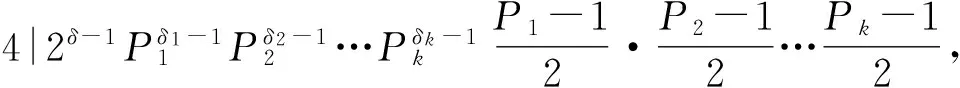
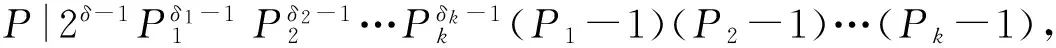
(5)

(6)

情况1δ=0.

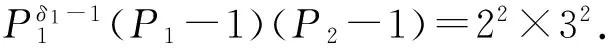
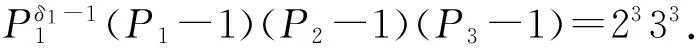
情况2δ≠0.

当δ1=1时，P1-1=2232，因而P1=37，从而n=2×37=74是方程(1)的解.

当δ1=2时，P1(P1-1)=2232.显然不存在奇素数P使得P1(P1-1)=2232成立，因而此时方程(1)无解.同理当δ1≥3时，方程(1)也无解.

当δ1=1时，(P1-1)(P2-1)=2333.由P1，P2的对称性以及其互异性，对于(P1-1)(P2-1)=2333，只需考虑以下几种情况：当P1-1=2，P2-1=22×33时，P1=3，P2=109，此时n=2×3×109=654是方程(1)的解；当P1-1=22，P2-1=2×33时，P1=5，P2=55，由于55不是素数，因而此时方程(1)无解；当P1-1=2×3，P2-1=22×32时，P1=7，P2=37，此时n=2×7×37=518是方程(1)的解；当P1-1=2×32，P2-1=22×3时，P1=19，P2=13，此时n=2×13×19=494是方程(1)的解.

当δ1=2时，P1(P1-1)(P2-1)=2333.从而P1=3，P2=37，此时n=2×32×37=666是方程(1)的解.

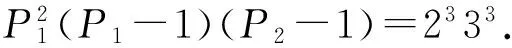
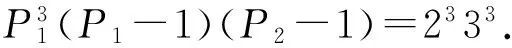
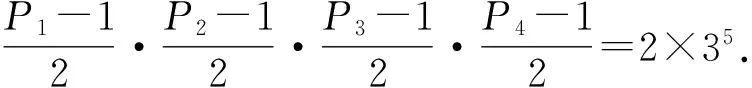
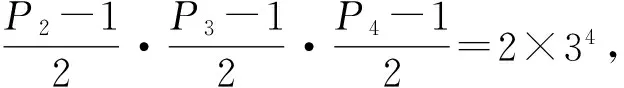
情况2.2δ=2，此时n=22P1δ1P2…Pk.

当δ1=1时，P1-1=2×32，因而P1=19，从而n=22×19=76是方程(1)的解；

当δ1=2时，P1(P1-1)=2×32.显然不存在奇素数P使得P1(P1-1)=2×32成立，因而此时方程(1)无解.同理，当δ1≥3时方程(1)也无解.

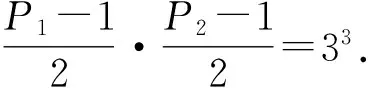
当δ1=2时，P1(P1-1)(P2-1)=2233，从而P1=3，P2=19，此时n=22×32×19=684是方程(1)的解.

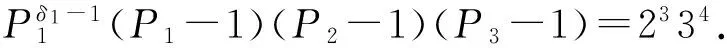
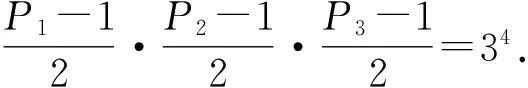
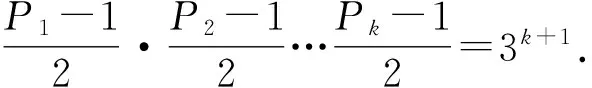
故方程(1)无解.同理当δ1≥2时，方程(1)也无解.

[参考文献]

[1]闵嗣鹤，严士健.初等数论[M].北京：高等教育出版社，2009：58.

[2]ERDÖS P.On the normal number of prime factors ofp-1 and some related problems concerning Euler’sφfunction [J].Quart J Math Oxford Ser，1935(6)：205-213.

[3]WOOLRIDGE K.Values taken many times by Euler’s phi-function[J].Proc Amer Math Sco，1976，76：229-234.

[4]POMERANCE C.Popular values of Euler’s function [J].Mathematika，1980，27：84-89.

[5]MASAI P，VALETTE A.A lower bound for a counterexample to Carmichael’s conjecture[J].Boll un Mat Ital，1982(2)：313-316.

[6]LEHMER D H.On Euler’s totient function[J].Bulletin of the American Mathmatical Society，1932，38(1)：745-751.

[7]柯召，孙琦.关于方程kφ(n)=n-1[J].四川大学学报(自然科学版)，1963(1)：13-21.

[8]SUN CUIFANG，CHENG ZHI.Some kind of equations involving Euler functionφ(n)[J].Journal of Mathematical Study，2010，43(4)：364-369.

[9]张四保.有关Euler函数φ(n)的方程的正整数解[J].数学的实践与认识，2014，44(20)：302-305.

[10]孙树东.一个与Euler函数φ(n)有关的方程的正整数解[J].北华大学学报(自然科学版)，2015，16(2)：161-164.

[11]张四保，刘启宽.关于Euler函数一个方程的正整数解[J].东北师大学报(自然科学版)，2015，47(3)：49-54.

[12]张四保，杜先存.一个包含Euler函数方程的正整数解[J].华中师范大学学报(自然科学版)，2015，49(4)：497-501.

[13]吕志宏.两个数论函数及其方程[J].纯粹数学与应用数学，2006，22(3)：303-306.

[14]吕志宏.一个包含Euler函数的方程[J].西北大学学报(自然科学版)，2006，36(1)：17-20.

[15]陈国慧.一个包含Euler函数的方程[J].纯粹数学与应用数学，2007，23(4)：439-445.

[16]马静.方程φ(n)=2tω(n)(t∈Z+)的解[J].安徽师范大学学报(自然科学版)，2009，32(1)：23-26.