基于继电反馈及模型参数的串级控制器设计

顾大可，王　健，张　鋆

(1.东北电力大学自动化工程学院，吉林 吉林 132012； 2.福建华电可门发电有限公司，福建 福州 350500)

0　引言

由文献[1]提出的继电整定方法是一种极简单且鲁棒性能好的自整定方法，它成功地应用在工业中，主要在蒸馏塔控制中发挥重要作用.继电整定法是用非线性的继电环节产生等幅振荡来替代手动的Z-N频域响应法，通过对临界值的估算求出PID参数.W.L.Luyben等人[2]提出一种变化的自整定方法(ATV)，通过理想继电反馈与关键点的幅相关系得出简单的计算公式；W.Li等人[3]运用ATV方法求出的临界估计值与理论值相比有-18%～+27%的误差；C.C.Yu[4]提出一种饱和继电反馈实验，得到的继电输出是类似于正弦的斩波波形，减小了因只考虑一次谐波而产生的误差，随着继电整定方法的发展[5-6]，该方法也逐渐被用在串级控制系统中[7-8]；1994年C.C.Huang[9]用理想继电器替代串级回路中原有控制器，修正控制器参数，得到相对较好的控制方法，成为继电反馈在串级控制中应用的先例.

ATV方法等多数继电整定方法都不依赖于模型，其整定规则一般选择具有普遍性的Z-N法或改进的Z-N法，但是对于部分控制对象而言，这类方法的效果并不理想.比如，一个一阶惯性时滞系统(FOPDT)和一个二阶惯性时滞系统(SOPDT)，他们可能具有相同的临界参数，如果得到的控制器适用于FOPDT模型，那么它一定不适用于SOPDT模型.因此，使用同一个PID控制器的2种被控对象不可能同时达到理想的控制效果.另外串级控制系统的提出主要是为了克服对象的惯性及延迟，针对惯性和延迟时间较大的被控对象尤为有效，它相对于单回路控制而言对外界扰动具有提前抑制的作用.Z-N法在整定这类被控对象时易产生较大的超调，控制质量较差.针对以上问题本文提出一种基于继电反馈及模型参数的PID串级控制方法，对带有迟滞的被控对象，控制效果较ATV法超调量更小，趋于稳定时间更快，最后通过仿真实验对提出的方法加以验证.

1　控制器设计

FOPDT和SOPDT的模型为：

(1)

(2)

根据阻尼特性在设计控制器时将被控对象分为两组：第1组为FOPDT和SOPDT的过阻尼及部分欠阻尼对象，即ζ≥0.707；第2组为余下SOPDT的欠阻尼对象，即ζ<0.707.如此分类的原因是SOPDT模型的阻尼系数大于一定值时可以近似为FOPDT系统，性能上具有相似性.[10]两组被控对象的控制器设计均参考H.P.Huang提出的一种补偿控制回路.[11]

1.1　第1组被控对象控制器设计

令系统开环传递函数为

(3)

设计第1组PID控制器方程为

(4)

其中τf=0.05Td.根据继电反馈得到的FOPDT参数带入(4)式得到PID控制器参数计算公式：

(5)

其中：ko=0.65，a=0.4，ωμ=2π/Tμ，Tμ和Kμ分别为继电反馈实验所得临界周期和临界增益值.

对于第1组被控对象来说PI控制器也可满足一定的控制需求，根据上述开环传递函数，得到PI控制器方程为

(6)

同样可得PI控制器参数计算公式：

(7)

其中：ko=0.55，a=0.4，ωμ=2π/Tμ，Tμ和Kμ分别为临界周期和临界增益值.

1.2　第2组被控对象控制器设计

对于第2组欠阻尼系统，PI控制器会对系统的稳定性产生极大影响，所以仅采用PID控制.

令开环传递函数为

(8)

第2组被控对象采用SOPDT模型，可得到PID控制器方程为

(9)

PID控制器参数计算公式：

(10)

其中：ko=0.5，ωμ=2π/Tμ，Tμ和Kμ分别为临界周期和临界增益值，kp和θ为SOPDT模型中的稳态增益和延迟时间.

2　模型参数辨识

对于高阶的惯性时滞系统来说，经过降阶处理后也可以适用于以上的整定方法.在公式(10)中，除临界周期Tμ和临界增益Kμ可通过继电反馈实验获取外，还有关于降阶后的SOPDT模型参数的未知量：稳态增益kp和延迟时间θ，所以对于降阶后的SOPDT模型参数为已知条件，然后再通过辨识后的ζ选择分组和控制器类型.稳态增益kp采用继电反馈方法辨识[12-15]，延迟时间θ和阻尼比ζ则通过θ，ζ和τ之间的非线性关系得到.

2.1　辨识参数kp

为了得到kp，首先对继电反馈实验进行初始化，初始化的方法是使设定点或对象的输入人为加入扰动，扰动时间不宜过长，随后恢复原始值.

根据继电反馈曲线得到稳态增益[14]

(11)

当t>T时，继电反馈实验产生等幅振荡，且yI和uI同步振荡，yI和uI分别见图1中定义的平均值，kp计算公式为

(12)

2.2　辨识参数θ，ζ和τ

图1　yI和uI振荡曲线

理想继电反馈实验结构如图2a所示，被控对象的输出经过纯滞后时间θo后开始振荡，最终达到稳定，等幅振荡的幅值为A，周期为Tμ，且通过输出响应曲线得到一组测量值：幅值Aθ和时间Tp(见图2b).

对于SOPDT系统，Aθ/A和θ/Tp与系统参数θ，ζ和τ的对应关系为[10]

(13)

此外还需满足幅相特性关系：

(14)

其中Kμ为继电整定实验所求临界增益.

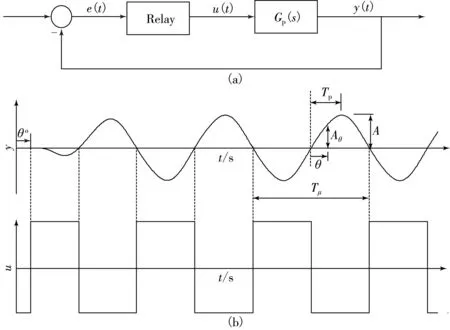
图2　理想继电反馈结构框图(a)和理想继电反馈输出响应曲线(b)

方程(13)中的θ与纯时滞θo并不等价，被辨识参数θ是高阶系统降阶后等价SOPDT模型中的延迟时间，而θo则是高阶系统本身具有的延迟时间，所以只有在高阶系统是SOPDT形式时θ与θo才相等.

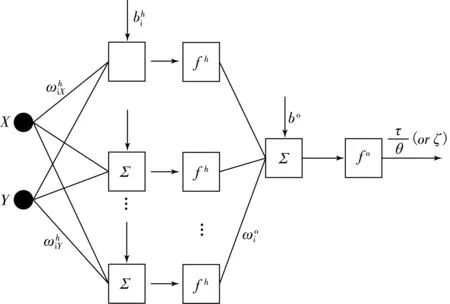
图3　神经网络结构

由于方程(13)是比较复杂的非线性函数关系，设计中采用BP神经网络的方法实现非线性函数的拟合，其网络结构如图3所示.

采用2个神经网络分别训练得到f1和f2函数关系.用于神经网络训练的输入值与目标值需要通过进行多组继电反馈实验获取，由于所得输入值分布太过密集，不便于训练，所以将2个输入值Aθ/A和θ/Tp转化成X和Y的形式：

(15)

对于已经训练好的神经网络，由于被降阶的高阶系统响应曲线上的θ值未知，所以能够得到多组τ/θ和ζ值，筛选出误差为

(16)

其中e为最小的一组，即为所求参数值.经过BP神经网络求得降阶后的SOPDT模型参数θ，ζ和τ值，通过ζ值大小选择控制器，完成PID参数整定.

3　PID串级控制系统

基于继电反馈的PID串级控制系统如图4所示.串级控制分为副回路和主回路，在C.C.Hang提出的串级继电整定方法中，主回路整定前副回路控制器已手动调节完成，即两步整定法，同样延用基于继电反馈的两步整定法实现PID整定.

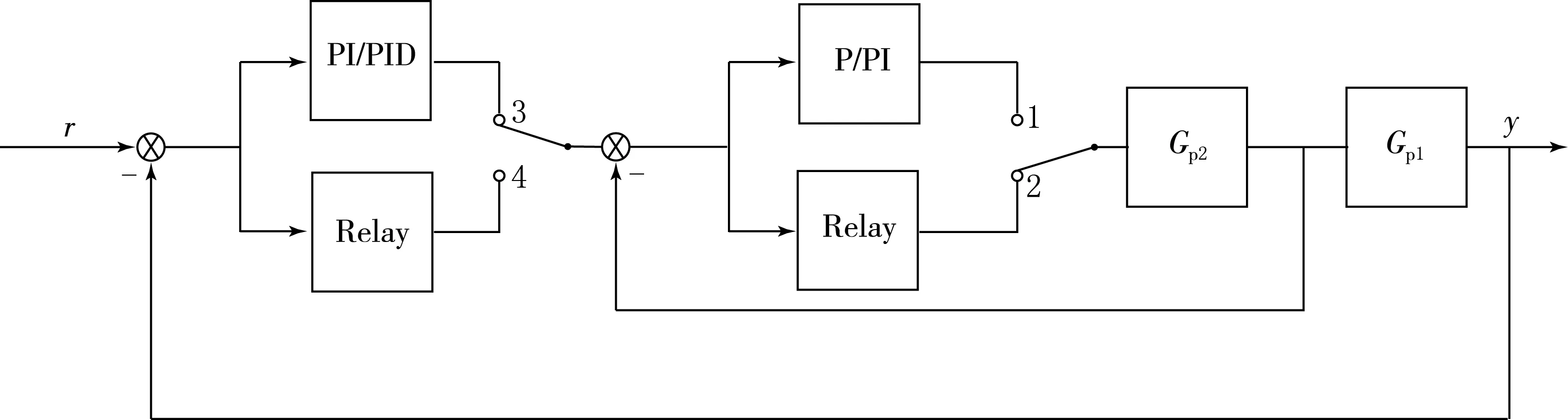
图4　继电反馈PID串级控制系统结构

当仅整定副回路时，开关置2(见图4)，副回路处于整定阶段，根据继电反馈实验得到临界参数Kμ2和Tμ2，判断副控对象类型，将高阶模型降阶，选择合适控制器类型合理设计副回路控制器.

当副回路整定完毕，开关置1，副回路处于控制阶段，主回路置4，处于整定阶段.利用上一节的模型参数辨识方法将副回路和主回路的被控对象看做是一个整体得到降阶后的SOPDT模型，其中θ的取值为θo至Tp区间.降阶完成后的等价模型根据ζ值选取控制器类型，结合继电整定方法得到临界参数Kμ1和Tμ1完成PID串级控制器参数整定.

4　仿真实验

用2个例子来验证方法的有效性.

实验1

(17)

整定串级控制系统的副回路，通过继电反馈实验得到Kμ2=2.28，ωμ2=20.43，副回路被控对象为FOPDT模型，选择公式(7)的PI控制器，其参数为Kp2=0.72，Ti2=0.13；将主回路接入，通过继电反馈实验的响应曲线结合神经网络方法求出θ=1.184，ζ=0.83，用公式(5)求得Kp1=0.72，Ti1=0.13，用公式(7)求得Kp1=0.701，Ti1=0.185，Td1=0.67.将基于模型的继电方法与ATV法的控制曲线进行对比(见图5).

实验2

(18)

断开主回路，继电反馈实验得到副回路的临界参数Kμ2=5.556，ωμ2=0.911 3，选择(7)式的PI控制器，其参数为Kp2=3.4，Ti2=6.16；将主回路接入，通过继电反馈实验的响应曲线结合神经网络方法求出θ=21.71，ζ=0.104 8，用(10)式求得PID控制器参数Kp1=0.725 9，Ti1= 30.853、Td1= 1.460 7.本文提出方法的PID控制曲线以及应用Z-N法的PI/PID控制曲线见图6.

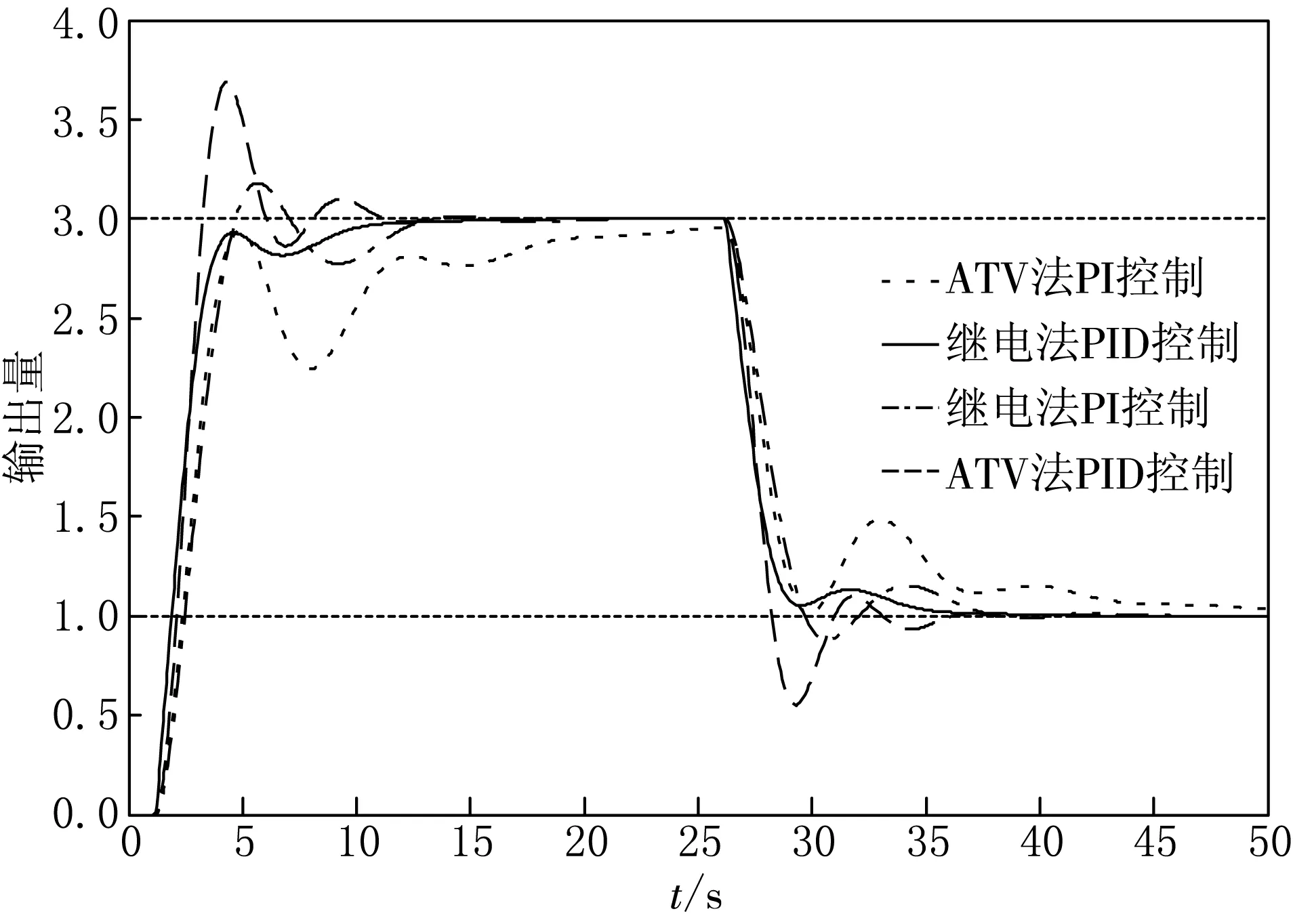
图5　实验1的串级系统控制曲线对比图图6　实验2的串级系统控制曲线对比图

从以上2个仿真图形中可以清晰地看到：基于模型的继电整定方法超调量小，趋于稳定时间较快，当外界扰动或设定值改变时，也能及时恢复稳定，但也存在一些问题，比如响应时间较ATV法慢，但总体的控制效果优于ATV法.

5　结论

针对串级控制系统提出了一种新的PI/PID整定方法，根据不同的参数模型之间的差异性把被控对象分为两组，对每组的对象提出不同的控制器参数整定方法，解决了部分被控对象由于传统继电整定方法不考虑模型结构而无法达到满意控制效果的问题.将主副回路分别结合继电反馈实验求出临界参数，主副回路被控对象当做整体作为主控对象，利用BP神经网络和继电反馈方法实现对高阶模型的降阶.该方法也同样适用于惯性和延时较大的系统.根据仿真结果可见，其控制性能优于Z-N整定方法.

[参考文献]

[1]HANG C C，ASTROM K J，Wang Q G.Relay feedback auto-tuning of process controllers：a tutorial review[J].Journal of Process Control，2002，12(1)：143-162.

[2]LUYBEN W L， Derivation of transfer functions for highly nonlinear distillation columns[J].Ind Eng Chem Res，1987，26(12)： 2490-2495.

[3]LI W，ESKINAT E，LUYBEN W L.An improved autotune identification method[J].Ind Eng Chem Res，1991，30(7)：1530-1541.

[4]YU C C.Autotuning of PID controllers，A relay feedback approach[M].Germany： Springer，2006：23-96.

[5]KIM J S，BYEON J，CHUN D，et al.Relay feedback methods for noisy processes[J].Aiche Journal American Institute of Chemical Engineers，2010，56(2)：560-562.

[6]TANG W，WANG Z F，ZHANG J G，et al.A relay feedback based autotuning PID controller and its application to pulp consistency control[C]// Proceedings of the 29th Chinese Control Conference.Beijing：IEEE，2010：3481-3485.

[7]PADHAN D G，MAJHI S.An improved parallel cascade control structure for processes with time delay[J].Journal of Process Control，2012，22(5)：884-898.

[8]MEHTA U，MAJHI，S.On-line identification of cascade control systems based on half limit cycle data[J].Isa Transactions，2011，50(1)：473-478.

[9]HANG C C，LOH A P，VASNANI V U.Relay feedback auto-tuning of cascade controller[J].Control Systems Technology，IEEE Transactions on，1994，2(1)：42-45.

[10]HUANG H P，JENG J C，LUO K Y.Auto-tune system using single-run relay feedback test and model-based controller design[J].Journal of Process Control，2005，15(6)：713-727.

[11]HUANG H P，JENG J C.Monitoring and assessment of control performance for single loop systems[J].Industrial and Engineering Chemistry Research，2002，41(5)：1297-1309.

[12]LIU T，WANG Q G，HUANG H P.A tutorial review on process identification from step or relay feedback test[J].Journal of Process Control，2013，23(10)：1597-1623.

[13]SANTOSH S，CHIDAMBARAM M.Tuning of proportional integral derivative controllers for critically damped second-order plus time delay systems[J].Indian Chemical Engineer，2015，57(1)：32-51.

[14]HUANG H P，JENG J C.Identification for monitoring and autotuning of PID controller[J].Journal of Chemical Engineering of Japan，2003，36(3)：284-296.

[15]SOLTESZ K，HAGGLUND T，ASTROM K J.Transfer function parameter identification by modified relay feedback[C]//American Control Conference.American：Proceedings of the IEEEXplore，2010：2164-2169.