基于深度学习和复杂空间关系特征的多尺度遥感图像检索
王生生,张宇婷
(吉林大学计算机科学与技术学院,吉林 长春 130012)
随着各种卫星和机载传感器的高速发展,产生了大量高分辨率遥感图像,这些图像被应用在许多领域并创造出巨大的价值.因此遥感图像处理和分析已成为近几年来一个热点课题.遥感图像检索是高分辨率遥感图像应用的重要部分.而在实际研究过程中,由于遥感卫星发射数目剧增、图像采集设备的更新换代以及光遥感图像的分辨率显著增强等变化,出现了图像数据量过大、数据尺度不统一、数据格式不规范等诸多问题,因此如何实现高效准确的遥感图像检索是非常重要的研究课题.
这些高分辨率的遥感图像清晰地展现了一个空间场景的真实情况,一个空间场景由若干实体以某种结构分布构成,因此有效的遥感图像检索算法必须在提取图像特征的时候综合以下2个方面:(1)实体自身特征;(2)实体间空间关系特征.其中空间关系包括距离、方向、拓扑等.而这2个方面特征也会因为数据源不同、数据格式不统一等产生视觉差异,比如光照情况影响实体自身颜色变化,拍摄角度影响实体自身形状的变化,数据源尺度不同导致同一场景中部分目标或目标的一部分消失、拓扑关系的变化等问题.3种尺度下的同一区域的遥感图像见图1,从图1可明显看出,由于尺度不同,同一区域的遥感图像颜色差异巨大,尺度变化导致部分实体变形或消失,因此颜色纹理等特征在此情况下并不适用.
图像检索在现实生活中的应用已经取得了十分优异的成绩,近年来基于内容的图像检索(CBIR)已经趋近成熟,所提出的一系列算法包含各类底层特征也具有很强的鲁棒性.例如基于颜色直方图的图像检索算法[1],使用HSV模型利用色调、明亮度和饱和度对图像进行特征提取;尺度不变特征变换(SIFT)算法[2],它在空间尺度中寻找极值点,并提取特征不变量;基于纹理特征的灰度共生矩阵(GLCM)算法[3],提取图像关于灰度级空间的特征,基于单个像素点进行,根据关联建立矩阵;基于形状的形状上下文(SC)算法[4],以点为基础提取特征,在底层特征的基础上,提出了一些新的算法.
BOW算法[5]将图像中的特征向量进行聚类,将生成的码本最终以多维向量形式表示,但这些对于遥感图像并不适用,因为遥感图像包含复杂的视觉内容与场景结构,且容易受到不相干噪声所干扰,因此出现了一些针对遥感图像的算法.Y.Yang等人[6]于2013年利用局部不变特征对图像的显著性进行评估,并调整参数设计了针对遥感图像的视觉词包(BOVW);E.Aptoula[7-8]于2014年提出AL算法改进了传统的CBIR,算法用主动学习方法来推进相关反馈在支持向量机分类器中的工作,有效地提高了检索精度;E.Aptoula[7]同时也提出一种结合形态纹理的描述符,提取特征形成“视觉形态”词袋,最终用直方图表达特征;B.Begum[9]于2015年提出了基于散列的近似最近邻搜索算法,将高维图像特征向量映射成紧凑的二进制散列码;B.Begum[10]同时还提出一种改进的全局形态纹理描述符应用于遥感图像检索的方法,使用圆形协方差直方图和旋转不变点三元组来描述特征;L.Zhang等人[11]于2016年提出针对遥感图像的三层检索方法,算法获取图像特征排序取得图像锚点,进行扩展查询;同年Z.Du[12]提出一种局部结构学习的方法,首次将拓扑结构融入遥感图像检索中.但对于空间场景的检索来说,上面的算法对空间关系特征的提取不够完整,对于尺度变化鲁棒性不强.本文提出基于深度学习和复杂空间关系特征的多尺度遥感图像检索,算法融合图像底层特征与空间结构特征.利用深度学习算法Faster R-CNN对遥感图像进行目标检测;利用Delaunay三角网提取遥感图像的全局空间关系结构特征;使用模糊形状模型[13]提取局部空间关系特征,模糊形状模型对于刚性形变的鲁棒性极强且提取的特征不受尺度光照等影响,有效地规避了由于数据源不同所带来的视觉差异.本文所提出的算法流程如图2所示.

图2多尺度遥感图检索流程
1 算法描述
1.1 基于深度学习的目标检测
在对空间场景进行特征提取前需要先进行目标检测,将空间场景分解为单个子目标,以便于后续对目标特征和目标之间特征的提取与相似性计算.本文使用Faster R-CNN算法(Faster Regions with Convolutional Neural Network features)实现,该算法可分为2个部分:(1)RPN网络提取候选区域;(2)Fast R-CNN网络对候选区域进行分类.
1.1.1候选区域生成
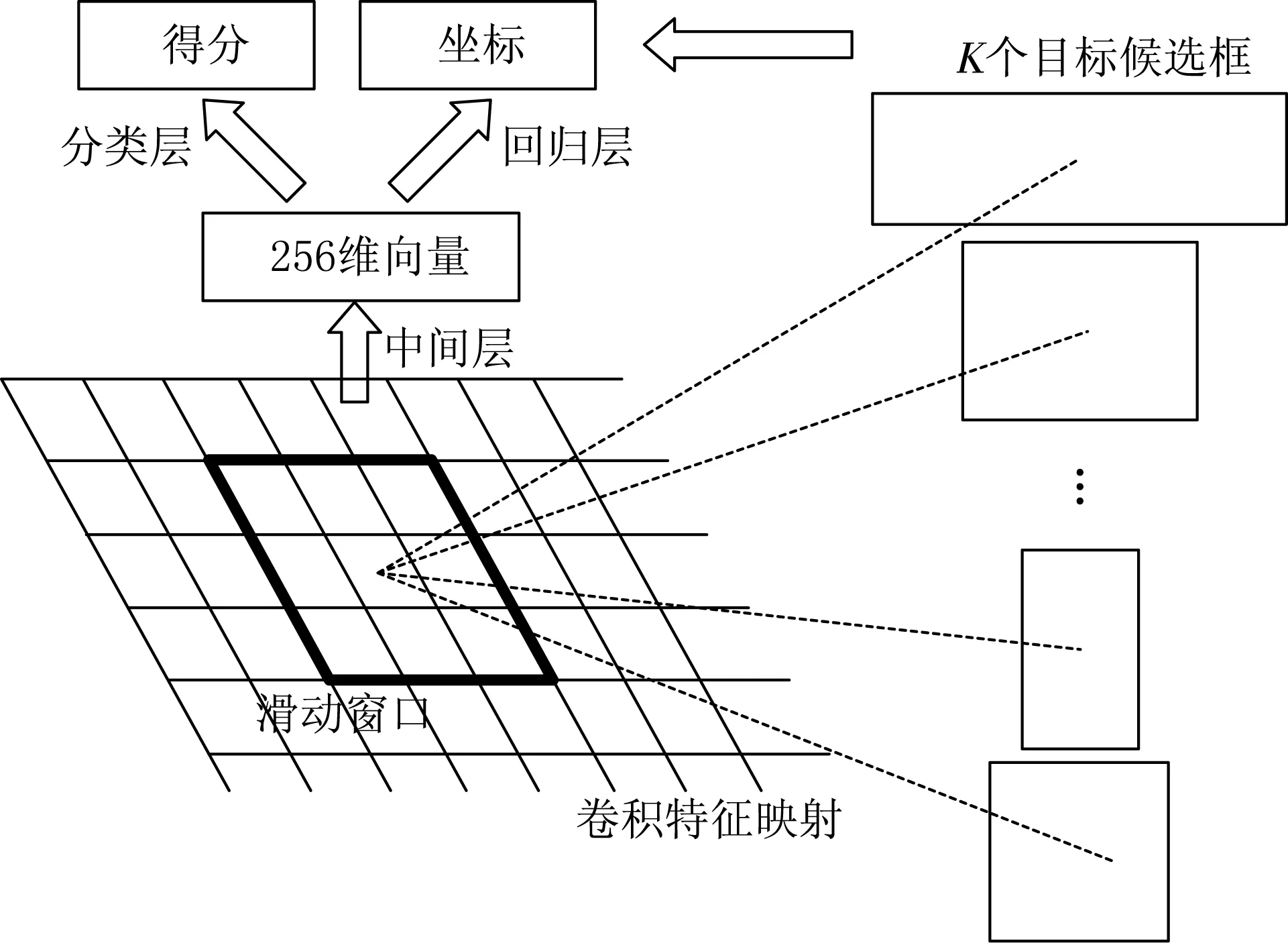
图3 RPN网络结构图
图像包含的信息十分复杂,其中的实体有不同的形状、尺寸、颜色、纹理以及实体在图像上的位置信息,因此提取时间复杂度较高.Faster R-CNN区别于其他使用SS(Selective Search)方法提取候选框的算法,将单张图片的特征提取时间降低了一个数量级.核心思想是利用卷积神经网络直接产生目标区域,设计了提取候选区域的网格Region Proposal Network(RPN),RPN是一个全卷积网络,其结构如图3所示.
1.1.2候选区域的分类
在多类别对象检测的场景中,Faster R-CNN中的RPN无法得知精确类别.但对于单一类别检测,在RPN中设置不同宽高比及尺度的候选框,不同尺度的候选框之间可以互相覆盖,送入网络中进行目标检测.网络最终输出2个向量:第1个是分类的标签及得分;第2个是位置.得到的标签依赖于程序在前期训练集的学习,对于本文数据集的特征,训练时只需要指定正负标签,即目标与非目标,网络将自主学习目标区域中的目标,即使尺度变换导致实体大小方向发生变化,实体所在几何中心相对位置也是固定的,因此Faster R-CNN对于遥感图像的目标识别不受尺度影响.
1.2 特征提取与匹配
1.2.1全局空间关系特征
考虑尺度因素对遥感图像空间关系的影响,一些小的目标在大比例尺图像上会消失,因此在多尺度遥感图像检索中会面对实体个数的增减等一系列问题,我们选择对差错点容错程度较强的方法,即使用本征参考系对空间关系进行描述.同时,考虑到实体的形状在不同尺度下差异较大,用实体几何中心之间的距离表示他们的距离关系,用相邻两条中心之间的连线夹角表示实体间的方向关系.考虑到不同尺度下绝对距离不同,将进行标准化处理.
空间场景图片经过Faster R-CNN处理以标注出所有单个目标,并返回目标的位置坐标.按照位置坐标提取每一个空间实体,用空间实体的几何中心代替这一实体在空间场景中的位置,实体间空间关系特征主要是距离和方向,这2种特征的表达都依赖于一个参照标准,为了满足局部匹配,需要提取具有局部拓扑不变性的特征.本文研究的对象为遥感图像,即多目标复杂空间场景,因此匹配成功的实体数目至少为3,因此我们选择稳定性最佳的三角形进行全局空间关系的匹配,将提取到的空间场景位置构造成对应的Delaunay三角网,将空间实体分组匹配,再选择全局空间关系特征相似的部分进行部分空间关系特征匹配.
遥感图像处理后返回的实体坐标及将坐标抽象成点集所构造的Delaunay三角网见图4.
因为点集构成的Delaunay三角网是唯一确定的,且三角网受单一元素影响较小,因此在尺度发生变化时出现实体增加或减少的情况,对算法的影响也很小,可以实现部分匹配.因此使用Delaunay三角网表示全局空间关系特征.
每一个三角形都表示空间实体之间的相对位置,由于三角形的稳定性,夹角固定的三角形三边比例一定相等,因此对任意两幅空间场景图片转化得到Delaunay三角网中的三角形进行了匹配.

图4 实体坐标(a)与Delaunay三角网的构造(b)
三角形特征相似定义:首先构造点集S的Delaunay三角网,其中由Si,Sj,Sk三点构成的一个△SiSjSk,这个三角形就对应这3个实体在图像上的空间关系特征,表示为
TRs(i,j,k)={∠SiSjSk,∠SjSiSk,∠SiSkSj}.
(1)
点集T由Ti,Tj,Tk三点构成的三角形△TiTjTk的特征可表示为
TRT(i,j,k)={∠TiTjTk,∠TjTiTk,∠TiTkTj}.
(2)
S由Si,Sj,Sk三点所确定的相对拓扑特征与T中由Ti,Tj,Tk三点所确定的相对拓扑特征之间的相似程度的表达式为
(3)
2个三角形的拓扑相似度度量为
SIMtopo=LA.
(4)
其中A和L分别代表两点集中的三点之间角度与距离的相似性度量,A表示角度偏差值.由于图像预处理误差,三角形的相似性在这里要重新定义,2个三角形角度之间允许有一定偏差,L为距离偏差,SIMtopo越小,S中由Si,Sj,Sk三点所确定的相对拓扑特征与T中由Ti,Tj,Tk三点所确定的相对拓扑特征越相似.遍历整个Delaunay三角网,对于S中的每个小三角形有一组T中的三角形序列作为候选待匹配,按照SIMtopo即拓扑相似度由低到高排序,选择前n个准备进行实体本身匹配,由实验可知n取5时效果最佳.
1.2.2局部空间关系特征
在完成全局空间关系匹配后,对于三角网中的每个小三角形进行局部特征关系的匹配,三角形的每一个顶点代表一个空间实体,三维实体的特征属性包括颜色、纹理、形状等,但在遥感图像中的空间场景由于来源不同,后期处理方式不同,图像中对于颜色、纹理的特征鲁棒性不强,因此采用模糊形状模型计算实体特征.
模糊形状模型是对其形状的一组关键点进行处理,使用网格装置对于不同梯度幅值的点进行分类描述,对相邻的区域关键点之间的空间关系进行运算,从而描述图像特征.
给定一组形成形状S的点S={X1,X2,…,Xm},对于每个点Xi∈S,叫做形状点.被视为一个特征用来计算模糊形状模型描述符.整个图像的区域被分割为N×N个形状大小相等的网格,每个网格上存在一些形状点,也可以从相邻区域的形状点上找到区域关系,因此,每个形状点都有助于本身的区域与相邻区域之间的模糊程度,并且网格的尺寸也标志了所允许的形状模糊水平,经过测试本实验选取16×16的网格已达到最佳效果.
首先将图片分成n×n个相等的子区域,用R表示,即R={r1,r2,…,rn×n},设Ci为每个区域ri的中心点,i∈{1,2,…,n}.N(ri)为ri的邻域,表示为
N(ri)={rk|rk∈R,|Ck-Cr|<2|g|}.
(5)
其中g为网格尺寸,对于每一个形状点更新特征向量表示为
(6)
再使用公式

(7)
将向量v进行标准化.
模糊形状模型的算法过程见图5,图5(a)为预处理后的目标,图5(b)为算法选取的特征点,图5(c)为最终得到的特征直方图.
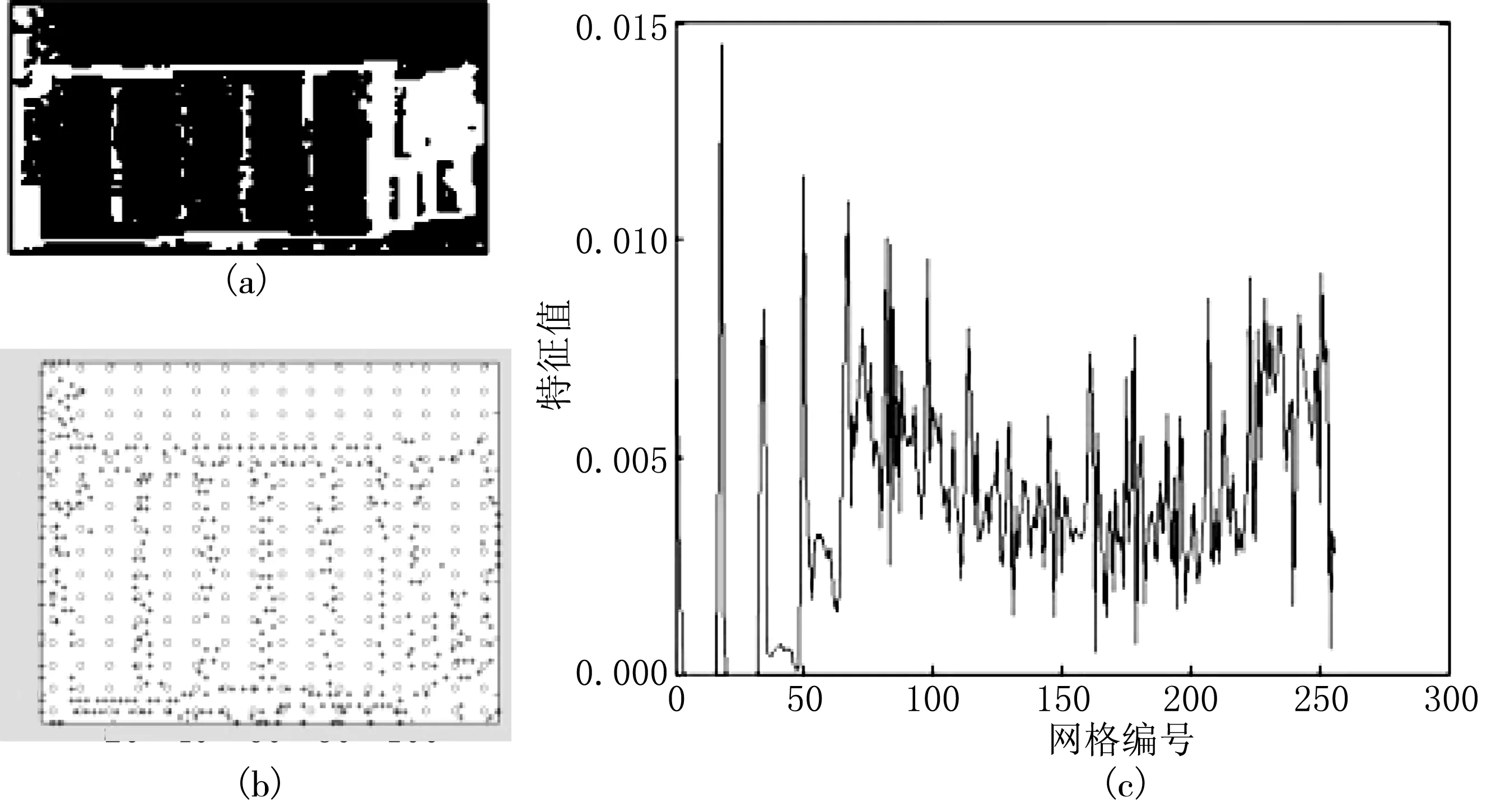
图5 模糊形状模型算法过程
1.2.3特征匹配
按照SIMtopo顺序寻找T中三角形对应的空间实体,对局部空间关系特征进行匹配.在进行局部空间关系匹配时只需要匹配代表局部图像的直方图,算法使用卡方系数方法进行匹配.
卡方系数是用于进行卡方检验的系数,是样本理论数据与真实数据的偏离程度,结果得到卡方值越小,证明样本理论数据越合理.卡方系数计算公式为
(8)
若代价值超过某一阈值则认为匹配成功,再进行下一组局部空间关系的匹配.假设匹配成功的空间实体数为K,待检索图像中空间实体数为E,然后最终两幅遥感图像的局部空间匹配率SIMlocal定义为
(9)
最终两幅遥感图像的匹配程度SIM值可表示为
SIM=(1-SIMtopo)*SIMlocal.
(10)
本文算法具体流程如下:
(2) 计算得出空间实体几何中心,构造Delaunay三角网;
(3) 对Delaunay三角网中的每一个小三角形描述并进行SIMtopo的排序;
(4) 构造每一个小三角形的局部空间关系特征,生成特征直方图;
(5) 按照SIMtopo顺序匹配直方图;
(6) 超过某一阈值视为成功匹配,继续匹配下一个,最终得到SIMlocal;
(7) 融合两种特征得到相似性,从大到小排序即为最终结果.
2 实验与分析
2.1 数据库
为了准确地评估本文方法的准确度,实验选择了具有不同视觉属性的光学遥感数据集.为了证明本文算法可部分匹配以及平移、旋转、缩放的不变性,手动对原始图片进行切割、旋转等操作.本文数据来自遥感图像的UC Merced Land-Use数据集[14]和RS19数据集[15-16].UC Merced Land-Use数据集来自美国国家地图局,它包含可见光谱中的空间高分辨率场景.手动标记过的数据集由2 100个遥感图像组成,每幅图像大小为256像素×256像素,分辨率为30.48 cm.包含农业、飞机、海滩、港口等21个分类,本文数据取自UC Merced Land-Use数据集中的buildings,dense residential,medium residential和sparse residential 4类.RS19数据集来自谷歌地图,包含从不同地区收集的高分辨率卫星图像.共1 005幅遥感图像,每幅图像的大小为600像素×600像素.包含19个分类,每类图像50张左右.本文数据取自RS19数据集中的commercial,industrial和residential 3类.这7类图像各有特点,residential图像分辨率高,包含丰富的特征在进行尺度变化时能够保留原有的精度,sparse residential图像分辨率适中,稀疏住宅图像特征单一,空间结构较为简单,处理时要注意有效特征的保留.为证明本文方法对于多尺度遥感图像检索的准确性,对于每类图像,经过处理、增加旋转、尺度放缩等变换.最终进行实验所用的数据集包含350张遥感图像,分为7类,每类50张.数据库部分示例如图6所示.
根据大量的实验可知,随着节点数目的增加,跳数在逐渐减少.由于随着节点数目的增加,可靠的下一跳节点数目也在增加,使得3种路由都选择距离目的节点最近的节点成为转发节点,减少了跳数.从图中可以明显的看出,RAR路由在节点数小于57时,其跳数远大于其他2个路由算法,而当节点数大于60时,其跳数逐渐接近于GPSR,而小于SLFB路由算法.这是由于当节点数少时,RAR路由算法寻找到的可靠下一跳节点并不是距离目的节点最近的节点,这就使得为了保证可靠性而去缩短了一跳的范围.但是随着节点数目的增加,同时节点的移动速度也比较慢,这就使得选取的下一跳节点更加容易是距离目的节点最近的节点,从而减少了跳数.

图6 数据集部分示例
数据库中图像经过目标检测之后能够准确找出空间实体的位置,实验中设置不同宽高比(a=h/w)和尺度(sc)的候选框,以及多种尺度的经过实验得到a的范围在[0.41,1.3]之间效果最佳,设置3种sc的大小分别为原尺寸的50%,100%和200%,在此期间的候选框可以最大程度的减少噪声影响.采取效果较好的VGG-16网作为骨干网,中间设置3个卷积层和2个同级一对一卷积层来实现分类与候选框的位置回归.候选框以8像素的步幅向原始候选区域回归,最终的检测误差小于15%,图7为密集住宅区目标识别后的结果.

图7 目标检测结果
2.2 全局空间关系特征
使用Delaunay三角网表达实体间空间关系,所提取的空间关系不受尺度变化影响,整体空间关系受局部影响较小,本质上是利用Delaunay三角网的唯一性和稳定性,为了测试上述匹配的效果,使用检索中常用的Top-N方法,给出99个形状不同的三角形进行测试.对于每个三角形进行相似度检索,取前10名的形状(Top-10),判断这10个三角形与原三角形的匹配程度.因为数据库中共有99个三角形,所以对于本次Top-10,最佳的结果便是99.实验结果见表1.从表1中可看出,算法在Top-1到Top-5效果显著,因此在特征融合时选择SIMtopo顺序前5的进行下一步匹配.

表1 Delaunay三角网检索结果
2.3 局部空间关系特征

图8 底层视觉特征检索结果示例
模糊形状模型在单一形状检索领域已经表现出很大的优势,算法在处理刚性物体时表现出很强的稳定性,因此本文首次将模糊形状模型应用在遥感图像中,算法提取特征生成二维特征直方图几乎能够完整地表示实体全部特征.经过实验证明,模糊形状模型描述符中网格的大小设置为16像素×16像素时为最佳.考虑到尺度不同图像精度的差异,对于空间实体匹配时选取100个点作为特征点,每个特征点将被描述为其邻域的6或9个权值,同一网格上所有特征点产生的权值相累加.最终将所有网格的特征值标准化后进行统计,生成整个形状的特征直方图.使用卡方系数进行匹配,按照代价值降序排列,检索结果实例见图8.通过图8可以看出,模糊形状模型对于空间实体的特征提取与表达正确率较高,说明算法对于空间实体的检索是有效的,作为空间场景匹配中的重要环节,精确度达到要求.
2.4 空间场景检索
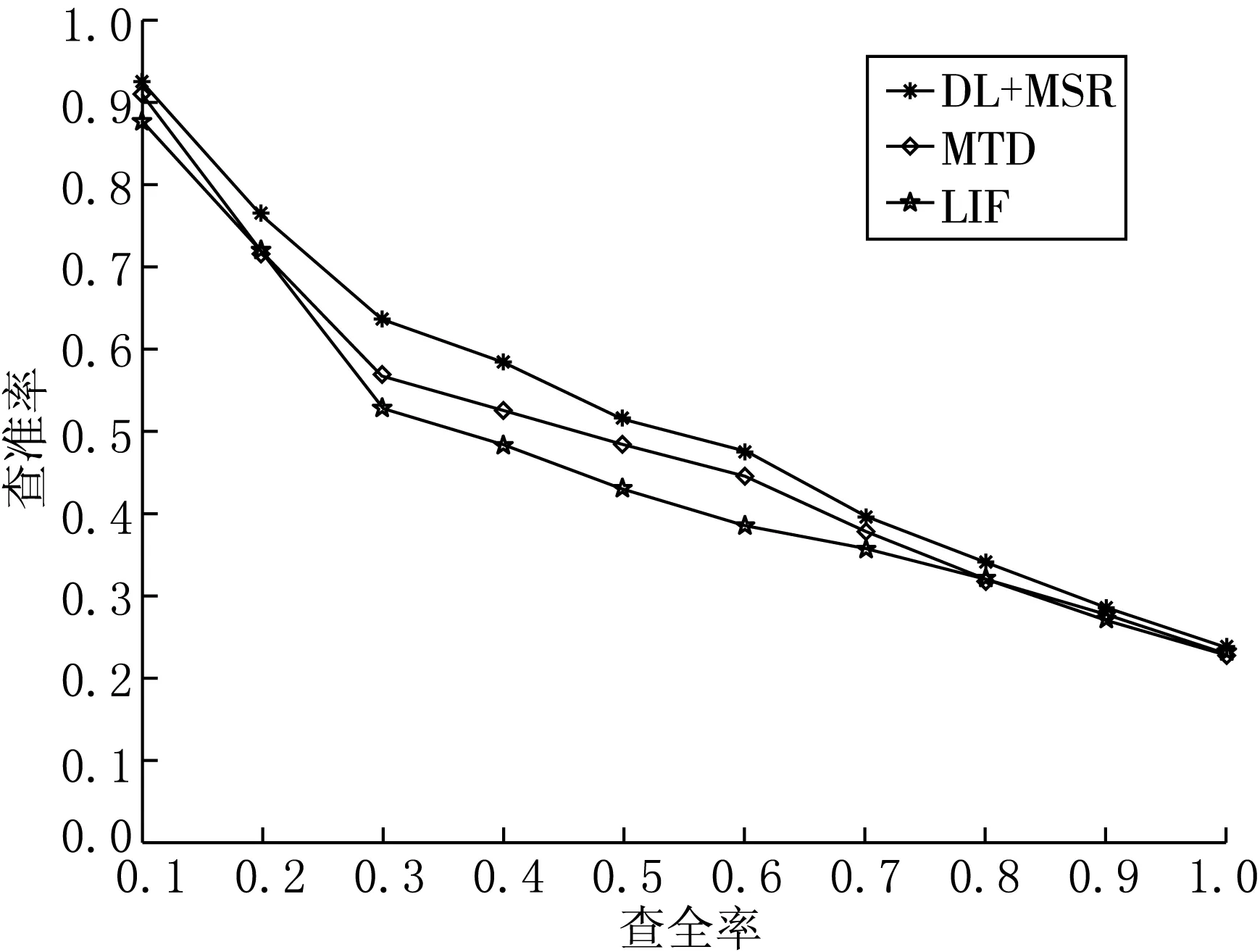
图9 3种方法的检索性能对比
按照空间关系排序后进行空间实体的匹配,最终按匹配程度给出序列.为了全面证明本文提出的算法对遥感图像空间场景检索的有效性,选择了2个在遥感检索中表现优秀的算法与我们提出的算法做比较.
第1种是利用局部不变性特征[6](Local Invariant Features)进行特征提取,简称为LIF,该算法设计了基于网格的局部特征提取并聚类生成视觉词包;第2种是结合数学形态学与全局纹理描述符的特征表达方法,叫形态纹理描述符[8](Morphological Texture Descriptors),简称为MTD.实验采用二分类问题常用的评价指标,查准率表示检索到的目标图像数与被检索的图像数的比值,查全率表示检索到的目标图像数与数据库中所有的图像数的比值.本文实验与其他2种算法的对比结果如图9所示.
考虑到检索结果的排名准确性,利用平均查准率(mean average precision,MAP)表示检索结果的准确性,理想检索结果集为A={A1,A2,…,An},共n个结果,实际检索结果集为B={B1,B2,…,Bm}共m个结果,检索序列实际排序值为R1(i),检索序列理论排序值为R2(i),MAP的计算公式为
(11)
当m 3种算法的MAP在7个类别中的结果如图10所示. 图10 3种方法的平均查准率对比 从实验结果可以看出,本文提出的算法在检索的整体性能上优于其他2种算法,LIF和MTD算法在处理多尺度且带有复杂结构信息的遥感图像时并未显出优势,在图10中也可以明显看出本文算法在稀疏住宅区上的检索效果不理想,因为稀疏居民区提供的空间关系特征不足,而在其他空间关系复杂类别上取得了预期的结果,证明了算法的有效性. 本文提出了一种基于深度学习和复杂空间关系的多尺度遥感图像检索算法.给出了匹配方案实现空间场景的检索.实验结果表明,本文提出的多尺度遥感图像检索算法优于其他在遥感图像检索领域表现较好的算法.区别于其他相关算法,本文算法融合了全局空间关系特征与局部空间关系特征,减少了尺度因素对特征表达的影响,增强了图像特征的表达能力,捕捉到了其他算法忽略的空间关系,实现了其他算法无法完成的部分匹配与多尺度匹配,提升了多尺度遥感图像检索的性能. [参考文献] [1]SURAL S,QIAN G,PRAMANIK S.Segmentation and histogram generation using the HSV color space for image retrieval[C]// 2002 IEEE International Conference on Image Processing.Newyork:IEEE,2002:589-592. [2]LOWE D G.Object recognition from local scale-invariant features[C]// 1999 IEEE the proceedings of the seventh IEEE international conference on.Kérkira:IEEE,1999:1150-1157. [3]HARALICK R M,SHANMUGAM K.Texture features for image classification[J].IEEE Transactions on systems,man,and cybernetics (SMC),1973,3(6):610-621. [4]BELONGIE S,MALIK J,PUZICHA J.Shape matching and object recognition using shape contexts[J].IEEE Transactions on Pattern Analysis & Machine Intelligence,2002,24(4):509-522. [5]JÉGOU H,DOUZE M,SCHMID C.Improving bag-of-features for large scale image search[J].International Journal of Computer Vision,2010,87(3):316-336. [6]YANG Y,NEWSAM S.Geographic image retrieval using local invariant features[J].IEEE Transactions on Geoscience & Remote Sensing,2013,51(2):818-832. [7]APTOULAE.Bag of morphological words for content-based geographical retrieval[C]// 12th International Workshop on Content-Based Multimedia Indexing.Klagenfurt:CBMI,2014:1-5. [8]APTOULAE.Remote sensing image retrieval with global morphological texture descriptors[J].IEEE Transactions on Geoscience & Remote Sensing,2014,52(5):3023-3034. [9]DEMIR B,BRUZZONE L.Hashing-based scalable remote sensing image search and retrieval in large archives[J].IEEE Transactions on Geoscience & Remote Sensing,2016,54(2):892-904. [10]DEMIR B,BRUZZONE L.A novel active learning method in relevance feedback for content-based remote sensing image retrieval[J].IEEE Transactions on Geoscience & Remote Sensing,2015,53(5):2323-2334. [11]WANG Y,ZHANG L,TONG X,et al.A three-layered graph-based learning approach for remote sensing image retrieval[J].IEEE Transactions on Geoscience & Remote Sensing,2016,54(10):6020-6034. [12]DU Z,LI X,LU X.Local structure learning in high resolution remote sensing imageretrieval[J].Neurocomputing,2016,207:813-822. [13]ESCALERA S,FORNÉS A,PUJOL O.Blurred shape model for binary and grey-level symbolrecognition[J].Pattern Recognition Letters,2009,30(15):1424-1433. [14]YANG Y,NEWSAM S.Bag-of-visual-words and spatial extensions for land-use classification[C]// Sigspatial International Conference on Advances in Geographic Information Systems.San Jose:ACM,2010:270-279. [15]DAI D,YANG W.Satellite image classification via two-layer sparse coding with biased image representation[J].IEEE Geoscience & Remote Sensing Letters,2011,8(1):173-176. [16]XIA G S,YANG W,DELON J,et al.Structural high-resolution satellite image indexing[J].ISPRS TC VII Symposium-100 Years ISPRS,2010,38:298-303.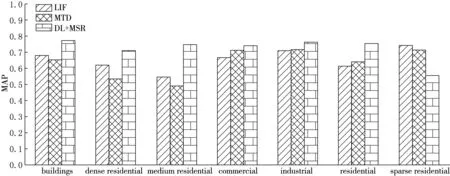
3 结论

