两体耦合腔阵列的PT相变和单光子传输

薛立飞，朱红波

(东北师范大学物理学院，吉林 长春 130024)

0　引言

自从C.M.Bender等人[1-2]提出了PT对称的概念以来，PT对称理论的潜在应用已经吸引了众多学者的研究兴趣.当参数达到某一临界值时，PT对称的非厄米系统将会发生相变，这一临界值称为异常点，也称为自发的PT对称断裂点(EP).[1-3]当参数低于异常点时，非厄米哈密顿量的本征值为实数；当高于异常点时，哈密顿量的本征值部分或全部为复数，这种现象通常被看做是PT对称性破缺.PT对称性破缺将导致一系列有趣的现象.例如，人们已经在PT对称结构中观察到了非相互作用的单光子传输[4-10]，并预测了由于场局域化而引起的非线性相互作用的加强.[11-12]PT对称系统在各个领域都有潜在的应用，如量子计算、耗散现象、超声波光学混沌等.[13-14]另外，耦合腔系统广泛应用于连续地控制光子传输.在无限长耦合腔阵列中，可以引入破缺来构建频率转换器[15]、单光子开关[16-17]和路由器[18].目前，人们已经可以实现两体耦合腔的实验，例如状态传输[19]与相干极化[20].

本文研究了PT对称的两体耦合腔系统，该体系由对称的光场增益和耗散的两腔组成，并且两腔之间具有线性耦合，构成了耦合腔阵列.分析了该体系的PT相变以及PT对称相和对称破缺相中的单光子传输特点.

1　体系模型与PT相变

研究系统是一个有PT对称性的两体耦合腔阵列，2个单模腔(A和B)中分别有光场的耗散(腔A)和增益(腔B)，并且增益腔与耗散腔之间发生线性耦合，如图1所示.

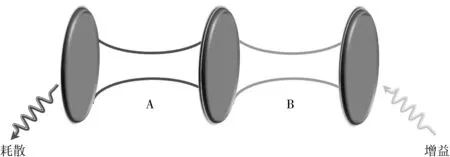
A腔有光场的耗散；B腔有光场的增益

对于这个两体耦合腔系统，令ћ=1，体系的哈密顿量可写为

(1)

其中：a1，a2(a1+，a2+)分别是耗散腔A与增益腔B的光场湮灭(产生)算符；ω1，ω2分别是两腔的谐振频率；J是两腔之间的线性耦合系数，其大小可以通过改变增益腔与耗散腔之间的距离来调节；γ1(γ1>0)是A腔的光子数耗散率；γ2(γ2>0)是B腔的光子数增益率.在研究体系PT相变的过程中，考虑两腔的谐振频率相同(ω1=ω2=ω)和光子数的增益率与耗散率相同(γ1=γ2=γ)的情况下，此时哈密顿量满足PT对称性即[H1，PT]=0.这里P表示空间对称算符1↔2，T表示时间反演算符it↔-it[1].

其中N±是正交归一化常数，为了方便我们把|E±〉写作两分量向量，并且

a：E±的实部随J/γ变化规律； b：E±的虚部随J/γ的变化规律；c：|a±|随J/γ的变化规律图2　两体耦合腔的透射率

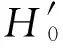
E±的实部和虚部随J/γ的变化规律及分量的相对几率幅绝对值随J/γ的变化规律见图2(ω=5γ，γ=1).由图2可以看出，系统的本征值是对称分布的.在PT对称相中，增益的光子快速地从增益腔转移到耗散腔，光子在增益腔和耗散腔中对称分布；当J=γ时系统发生PT相变，在PT对称性破缺相中，增益的光子也是从增益腔转移到耗散腔，足够长的时间过后，光子局域化在耗散腔中.

2　单光子传输

(2)

(3)

2.1　单光子在PT对称相中的传输

研究单光子在PT对称相中的传输行为.此时J>γ，首先考虑初始时刻单光子在耗散腔中的情况，即α(0)=1，β(0)=0.通过计算获得光子分别在两腔中的概率幅为：

(4)

(5)

(6)

(7)

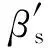
a：初始时刻光子在耗散腔中；b：初始时刻光子在增益腔中

2.2　单光子在PT对称性破缺相中的传输

单光子在PT对称性破缺相中传输，J<γ.首先考虑初始时刻单光子处于耗散腔，即α(0)=1，β(0)=0，通过计算可以明确获得光子在两腔中的概率幅为

(8)

(9)

(10)

(11)

单光子在两体耦合腔系统PT对称性破缺相中传输的概率如图4(ω=10γ，J=0.5γ，γ=1)所示，分别给出初始时刻单光子处于耗散腔和增益腔.图4中所展示的动力学性质与上面PT对称相的情况截然不同.但是，同样在PT对称性破缺相中也可以观察到单向性的现象.如图4a，当单光子初始时刻处于耗散腔，光子将首先经历耗散，然后在增益腔内的增益将补偿耗散，随着时间的推移，光子处于增益腔内的几率将增大，而在耗散腔中光子的几率先减小之后也将增大.图4b是初始时刻单光子处于增益腔中的情况.在这种情况下，增益效应随着时间逐渐展现出来，并且在所有腔里找到光子的可能性是随时间单调递增的，但是在增益腔中增加的更快.所以在PT对称性破缺相中也表现出了单光子传输的单向性.

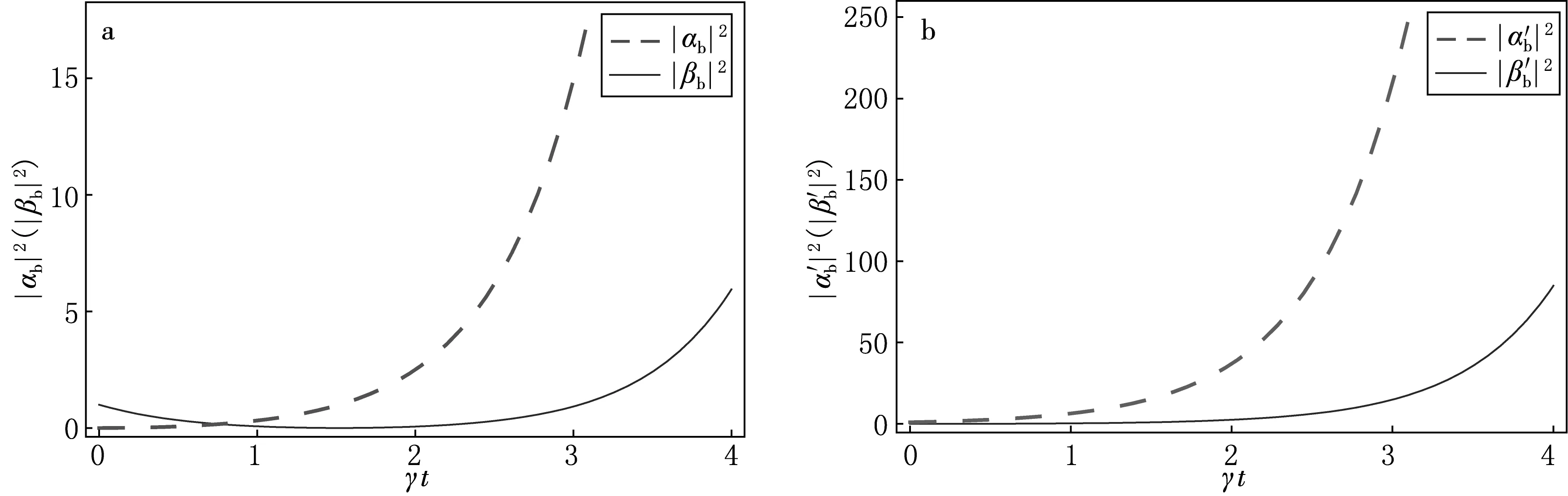
a：初始时刻光子在耗散腔中； b：初始时刻光子在增益腔中

3　总结

研究了有对称增益和耗散的两体耦合腔阵列的PT相变.在PT对称相中所有的本征值都是实数，对应的本征态在增益腔和耗散腔中对称分布；在PT对称性破缺相中本征值出现复数，并且出现场局域化现象.随着PT对称相变的出现，单光子在两相中的传输行为也存在差异.结果表明：当光子由PT对称相向PT对称性破缺相传输时，周期性的动力学性质被破坏，但是光子在两相中的传输都具有单向性.这些研究方法可以推广到具有PT对称的三体耦合腔阵列，以及多体耦合腔阵列体系.对日后基于耦合腔阵列的光学设备的研究有一定的帮助.

[参考文献]

[1]BENDER C M.Making sense of non-Hermitian Hamiltonians[J].Reports on Progress in Physics，2007，70：947-1018.

[2]BENDER C M，BOETTCHER S.Real spectra in non-Hermitian Hamiltonians having PT symmetry[J].Physical Review Letters，1998，80(24)：5243-5246.

[3]MOSTAFAZADEH A.Pseudo-Hermiticity versus PT symmetry：the necessary condition for the reality of the spectrum of a non-Hermitian Hamiltonian[J].Journal of Mathematical Physics，2002，43(1)：205-214.

[4]LIN Z，RAMEZANI H，EICHELKRAUT T，et al.Unidirectional invisibility induced by PT-symmetric periodic structures[J].Physical Review Letters，2011，106(21)：213901.

[5]BENDER N，BODYFELT J D，RAMEZANI H，et al.Observation of a symmetric transport in structures with active nonlinearities[J].Physical Review Letters，2013，110(23)：234101.

[6]WU J H，ARTONI M，LA ROCCA G C.Non-Hermitian degeneracies and unidirectional reflectionless atomic lattices[J].Physical Review Letters，2014，113(12)：123004.

[7]RAMEZANI H，KOTTOS T，ELGANAINY R，et al.Unidirectional nonlinear PT-symmetric optical structures[J].Physical Review A，2010，82(4)：1015-1018.

[8]CHANG L，JIANG X，HUA S，et al.Parity-time symmetry and variable optical isolation in active-passive-coupled microresonators[J].Nature Photonics，2014，8(7)：524-529.

[9]FENG L，XU Y L，FEGADOLLI W S，et al.Experimental demonstration of a unidirectional reflectionless parity-time metamaterial at optical frequencies[J].Nature Materials，2013，12(2)：108-113.

[10]LI J，ZHAN X，DING C，et al.Enhanced nonlinear optics in coupled optical microcavities with an unbroken and broken parity-time symmetry[J].Physical Review Letters A，2015，92(7)：043830.

[11]LI J，YU R，WU Y.Proposal for enhanced photon blockade in parity-time-symmetric coupled microcavities[J].Physical Review Letters A，2015，92(5)：053837.

[12]LUY X Y，JING H，MA J Y，et al.PT-symmetry-breaking chaos in optomechanics[J].Physical Review Letters，2015，114(25)：253601.

[13]WEST C T，KOTTOST，PROSEN T.PT-symmetric wave chaos[J].Physical Review Letters，2010，104(5)：054102.

[14]MEI B，XU H S，TU X L，et al.Origin of odd-even staggering in fragment yields：impact of nuclear pairing and shell structure on the particle-emission threshold energy[J].Physical Review C，2014，89(5)：675-687.

[15]WANG Z H，LI Y，ZHOU D L，et al.Single-photon scattering on a strongly dressed atom[J].Physical Review A，2011，86(2)：023824.

[16]ZHOU L，GONG Z R，LIU Y X，et al.Controllable scattering of a single photon inside a one-dimensional resonator waveguide[J].Physical Review Letters，2008，101(10)：100501.

[17]ZHOU L，YANG L P，LI Y，et al.Quantum routing of single photons with a cyclic three-level system[J].Physical Review Letters，2013，111(10)：103604.

[18]OGDEN C D，IRISH E K，KIM M S.Dynamics in a coupled-cavity array[J].Physical Review A，2008，78(6)：5175-5179.

[19]LIU Y C，LUAN X，LI H K，et al.Coherent polariton dynamics in coupled highly-dissipative cavity quantum electrodynamics[J].Physics，2014，112(21)：213602.

[20]FELICETTI S，ROMERO G，ROSSINI D，et al.Photon transfer in ultrastrongly coupled three-cavity arrays[J].Physical Review A，2014，89(1)：013853.